初始化对交通元胞自动机模型稳定性的影响

邓建华 冯焕焕 葛婷

摘要： 针对现有交通元胞自动机模型运行初始不稳定，数据输出存在较长时间的初始波动问题，基于Fisher-Yates算法原理，设计出一种新的交通流初始化方法。该方法可以确保车辆从进入元胞空间到随后的演化更新，其位置及更新时机的随机性。通过对采用新交通流初始化方法的模型进行演化实验，结果表明：任意空间占有率条件下交通流的初始波动区间都在50步以内；当演化更新总步数达到3 600步时，模型剔除初始波动区间的输出数据已充分收敛，这时模型运行已足够稳定。

关键词： 元胞自动机；交通流初始化；Fisher-Yates算法；初始波动区间

中图分类号： U491.1文献标识码： A

收稿日期： 2021-12-01；修回日期：2022-03-18

基金项目： 国家自然科学基金（51808370）；苏州科技大学基金项目（341311108;XKQ201305）

第一作者： 邓建华（1972-），男，湖南永兴人，硕士，副教授，主要研究方向为交通复杂系统仿真。

Influence of the Initialization Method on the Stability of Traffic Cellular Automata Model

DENG Jianhua， FENG Huanhuan， GE Ting

（College of Civil Engineering， Suzhou University of Science and Technology， Suzhou 215011，China）

Abstract：Aiming at the initial instability of the existing traffic cellular automata model and the initial fluctuation of data output for a long time， a new traffic flow initialization method is designed based on the principle of Fisher-Yates algorithm. This method can ensure the randomness of the location and update timing of the vehicle from entering the cell space to the subsequent evolution and update. Through the evolution experiment of the model using the new traffic flow initialization method， the results show that the initial fluctuation range is within 50 steps under the condition of arbitrary space occupancy; When the evolution update reaches 3600 steps， the output data of the model after excluding the output of the initial fluctuation interval has converged enough， and the operation of the model is stable enough.

Key words： cellular automata; traffic flow initialization; Fisher-Yates algorithm; initial fluctuation range

0 引言

元胞自動机是一类时空离散的网格动力学模型［12］，是交通流建模的主要工具之一。交通元胞自动机模型的元胞单元、邻域结构、元胞空间及演化规则一旦确定，作为人工设计的方法，交通流初始化是否合理就可能是影响模型稳定性的主要因素。现有的交通流初始化方法源自于Nagel和Schreckenberg［3］1992年提出的NaSch模型。NaSch模型用一个单维的元胞单元数组构成的元胞空间来表示一段单车道公路，并为它设计了开放性、周期性两种边界条件。开放性边界设计有两个开放端：一端为车辆驶入端，另一端为驶离端；周期性边界使元胞空间构成一个两端首尾相连的环。在此基础上，NaSch模型对这两种边界条件提出了相应的交通流初始化方法：对于开放性边界条件，模型首先生成一个随机数列，该数列元素值与车辆输入时刻相关联，数列的大小等于输入的车辆总数。模型演化时，车辆按照该数列的元素值所示的时刻进入元胞空间，如果驶入端的首个元胞单元为空，则把车辆布置到该元胞单元，如此反复，直到所有车辆进入元胞空间，则完成了模型的交通流初始化过程。该初始化方法实现了车辆进入元胞空间在时间上的随机性；对于周期性边界条件，模型首先按照待输入车辆总数生成一个与每辆车输入位置相关联的随机数列，然后，根据该数列每位元素值所标示位置把车辆一次性布置到元胞空间，从而完成模型的交通流初始化。这时，车辆的初始位置是随机的。NaSch模型的交通流初始化方法的原理清晰，实现过程简单，是现有交通流元胞自动机模型交通流初始化的通用方法［4］。但是，按照上述两种方法完成交通流初始化以后，模型还需要通过遍历元胞空间来对所有的车辆进行状态更新，越靠近车流下游的车辆越会优先得到更新［45］。这种仅能确保车辆初始时刻或初始位置随机分布的交通流初始化方法，也带来了其它相关问题，如：元胞空间内前导车的更新时机总会优先于跟驰车辆，导致跟驰效应的削弱［6］。为改善这些缺陷则需增加额外的演化规则，如：随机减速规则、随机慢启动规则等，才能再现车辆跟驰过程中的时走时停、迟滞等交通现象［710］。20世纪末，RICKERT等［11］提出了著名的STCA双车道模型，随后DAOUDIA等［12］提出了三车道模型，他们都沿用了NaSch模型的交通流初始化方法，随后也被其它多车道元胞自动机模型沿用至今［1316］。如前述，交通流经初始化后，车辆的演化更新需通过遍历元胞空间来实现，该过程也对多车道模型中的换道行为描述产生不利影响，如，换道冲突事件会被忽略掉，而这种因换道产生的车辆冲突在现实多车道交通流中却很常见［17］。综上所述，仅能使车辆初始时刻或初始位置随机分布的交通流初始化方法，会导致模型对车辆个体行为描述的偏差，这种偏差既会影响车辆运行状态数据的准确性也会延缓交通流的自组织过程［18］。

基于Fisher-Yates算法［19］的基本原理，本文提出了一种新的交通流初始化方法，该方法可以确保车辆从进入元胞空间到随后的演化更新，其位置及更新时机的随机性，基本还原现实交通流中车辆运动行为的时空随机特性，理论上也可加快交通流的自组织过程，提高模型运行的稳定性。为进一步验证该观点，本文对新提出的交通流初始化方法进行较为详细的实验研究，并结合实验研究所得到的初始波动区间值对模型演化更新总步数提出了建议。

1 模型的元胞空间及演化规则

1.1 模型的元胞空间

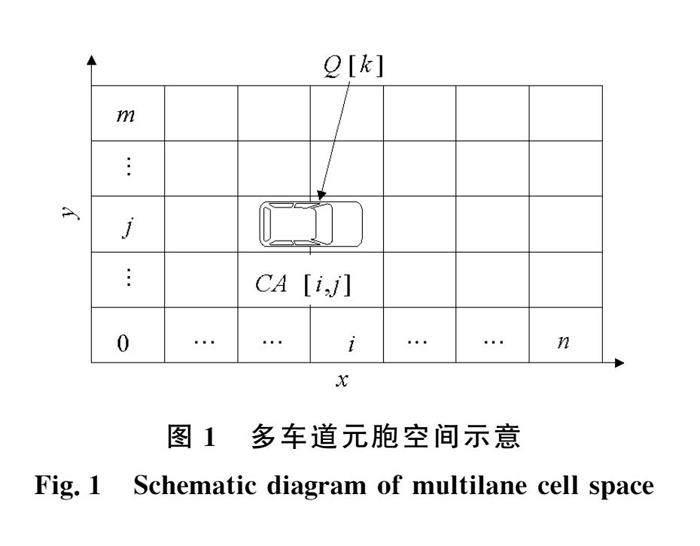
为表示本文提出的交通流初始方法具有通用性，这里选择构建一个多车道元胞自动机模型的元胞空间。该空间由一个二维Moore型邻域的单位元胞数组来描述，以表示一段多车道路段。如图1所示，假设该元胞空间由n×m元胞单元构成，则它可表示为CA［n，m］，其中x轴表示道路纵向；y轴表示道路横向。单位元胞横向宽度与车道同宽，单位元胞长度根据车辆的最大加（减）速度来设置（参见后续的实验设计）。一辆车可能占据多个元胞单元，车辆所处的位置用其前保险杠所处的元胞单元来标识，如车辆Q［k］的位置在元胞单元CA［i，j］。这里的Q［k］为待输入系统的车辆队列Q［w］中的一个元素，k=0，…，w-1，其中w为车辆总数。

为控制设定的演化更新步数内元胞空间中的车辆数恒定，以观察、分析系统的稳定情况，本文的元胞空间采用周期性边界条件。

1.2 模型的演化规则

该多车道元胞自动机模型的跟驰规则采用NaSch模型的基本规则，以尽可能减少规则冗余对模型的稳定性产生影响；换道规则采用文献［20］提出的可以处理换道冲突的换道决策模型。设元胞空间CA［i，j］单元上的车辆Q［k］从t→t+1演化更新一步的具体演化规则为：1）加速，vk（t+1）→min（vk（t）+1，vmax）；2）确定性减速，vk（t+1）→min（vk（t），dk）；3）随机慢化，当概率p，vk（t+1）→min（vk（t）－1，0）；4）换道决策，确定换道目标；5）目标位置更新，xk（t+1）→xk+vk（t+1）。其中，dk为跟车间距；随机慢化概率p=0.01；加（减）速度值为1单位元胞长/步2，可以表示为1cell/s2。单位“步”用“s”表示，下同。车辆更新后的速度为vk（t+1），位置为xk（t+1）。

2 基于Fisher-Yates算法原理的交通流初始化方法

模型演化更新前需要进行交通流初始化。Fisher-Yates算法［19］是一种复杂度不高的乱序算法，它可快速生成一个无偏、无重复元素的随机数列。基于Fisher-Yates算法原理，本文提出了新的交通流初始化算法，其具体描述为：

1）开始。这时模型的元胞空間CA［n，m］，边界条件与规则已确定。

2）初始化CA［n，m］与车辆队列Q［w］。设两个数组的元素初始值为零。

3）创建临时一维数组A［n×m］。它有n×m个元素，元素值依次为0到n×m-1。

4）把A看作一副有n×m张的扑克牌，对A进行乱序洗牌，然后开始抓牌。第k次抓到的牌值Q［x］正是车辆Q［k］将要布置在元胞空间的位置。如此反复，直到w张牌抓完、车辆布置完，表示该初始化过程结束。完整的算法流程如图2所示。

以上以周期性边界条件为例进行了算法描述，但该算法也适用于开放性边界条件的交通流初始化。当元胞空间为开放性边界条件时，算法仅需把数组A的大小设置为完成所有车辆输入需花费的演化更新步数，其余保持不变。

按照该算法流程进行交通流初始化以后，车辆队列Q［w］中的车辆Q［k］被随机布置在元胞单元CA［i，j］，并设CA［i，j］=1表示有车占据。同时CA［i，j］的位置信息也被回传给车辆Q［k］。这样，Q［k］始终与当前所处的元胞单元形成一一映射关系。由于Q［w］的每辆车一直保留着它们在元胞空间中的当前位置信息，交通流初始化以后的车辆演化更新可通过遍历Q［w］来实现，该过程使元胞空间中车辆的状态更新与现实交通流中车辆的运动行为改变具有基本一致的随机时空分布特性。这从根本上解决了遍历元胞空间需按一定时空顺序更新车辆的问题。

3 实验设计

3.1 实验目的与任务

模型演化更新时，车辆从交通流初始化设定的状态瞬间改为由规则驱动，该过程必然会造成车辆行驶状态的明显波动。考虑到这种波动会对研究成果产生潜在的影响，大多数学者采用了尽可能延长演化更新步数且仅截取演化尾端数据的做法来解决这个问题。但是，因为初始波动区间未知，学者们在设置演化更新总步数及尾端截取区间上不统一，常见设置的演化更新总步数为104～106 s、尾端数据截取区间为103～104 s［2123］。演化更新步数和截取区间设置不合理会造成计算资源的浪费，结合本文研究目的，把确定初始波动区间及合适的演化更新总步数作为本实验任务。

3.2 实验参数设置

为排除小尺度元胞空间对实验结果产生潜在干扰，设元胞空间周长L=20 000个元胞，单位元胞长度设置为0.98 m，则L的实际长度为19.6 km。单位元胞横宽为3.75 m，等于车道宽。实验场景假设为一段三车道的城市主干路，其设计计算速度为60 km/h。道路上的车辆为单一类型的小汽车，车身长为4.9 m，相当于5个单位元胞长。

设空间占有率D表示为

D=∑wk=1lkLanes×L0

其中，lk为第k辆车的长度，Lanes为车道数。

3.3 实验过程

某D值条件下，完成设定演化更新步数的演化过程称为一次实验。将D值区间划分为20等份，同一演化更新步数的20等份的D值所对应的20次实验构成一组实验。实验过程总体上按组进行，第1组演化更新步数最短，设为600 s。必要时可按每600 s递增重新做一组实验，如第2组实验可设演化更新步数为1 200 s重新进行实验。每做一组实验，都可进行初始波动区间的观察和输出数据的收敛情况分析。

輸出数据的收敛判定，采用公式（2）：

1－ε

其中，ε为收敛阈值，设ε=5%。f、f+1分别表示前一组、当前组实验； i为各空间占有率等分值所对应的序号，即i=0，…，19；则afi、af+1i分别为前一组、当前组相应D值点对应的数据值。

按照上述实验设计，先确定初始波动区间，再确定合适的演化更新步数。在确定合适的演化更新步数时，把初始波动区间输出的数据剔除，这样的研究分析结果会更准确，数据收敛更快。

4 实验结果与讨论

4.1 初始波动区间分析

按照实验设计，首先需要通过观察20个不同D值下输出的时斑图，分析确定初始波动的区间范围。限于篇幅，在不影响观察规律的情况下，这里仅等距列出了5个D值的时斑图，如图3所示。时斑图中：竖轴t表示演化更新步数，输出范围t=0～100 s；横轴x表示车辆行驶的距离，输出范围x=0～200 cells。图3中间部分黑色斜线表示车辆的行驶轨迹，处于波动区间的车辆轨迹会交叉形成局部聚集不均匀黑斑和空出的白斑，在图3的右上角用EI标识了能观察到的波动区间范围。从图3中可看出：D≤0.1或D≥0.9时车辆的初始波动很难观察到，这应该与低占有率情况下的车辆处于不受其它车辆干扰的自由行驶状态及高占有率情况下的车辆处于其它车辆严格约束的全阻塞状态有关；波动较明显的D值区间在D=0.3～0.7，且EI范围都不超过50 s，远小于目前大部分研究所设定的剔除范围［2123］。

4.2 模型稳定性分析与合适的演化更新总步数

按照前述的实验设计，重新从600 s开始进行分组实验，每次数据统计先剔除EI=50 s区间的输出数据，并绘制“速度-D图”与“流率-D图”，分别见图4和图5。从图4，5可以看出：曲线在D=0.4～0.8区间仍存在一些波动，当初始波动排除之后，该部分波动可以理解为模型演化过程中车辆受模型规则驱动的自组织过程。当演化更新总步数达到3 600 s时，曲线与前一组（2 400 s）曲线已基本重合。把这两组曲线的数据按照公式（2）列于表1中进行判定，发现：流率曲线最大实际ε=2.99%，速度曲线最大实际ε=3.63%，都在5%以内，说明这时的模型输出已充分收敛，模型运行已相当稳定。

5 结论

本文提出了一种交通元胞自动机模型交通流初始化的新方法，该方法可以确保车辆从进入元胞空间到随后的演化更新，其位置及更新时机的随机性，较已有交通流初始化方法能更好地还原现实交通流中车辆行进过程中行为的随机时空分布特性。对模型进行反复演化实验，发现新方法的初始化过程加快了交通流的自组织过程：交通流的初始波动区间都在50 s以内；当演化更新总步数达3 600 s时，模型输出的数据已充分收敛，表明这时模型的演化更新已相当稳定。本文实验研究所获得的初始波动区间及模型演化更新总步数可供相关研究参考。

参考文献：

［1］FOURRATE K， LOULIDI M. Disordered cellular automaton traffic flow model： phase separated state， density waves and self organized criticality ［J］. Eur Phys J B， 2006， 49（2）： 239-246.

［2］NASHINARI K， FUKV M， SCHADSCHNEIDER A.  A stochastic cellular automaton model for traffic flow with multiple metastable states［J］. Journal of Physics A： Mathematical and General， 2004， 37（9）： 3101-3110.

［3］NAGEL K， SCHRECKENBERG M. A cellular automaton model for freeway traffic ［J］. Journal De Physique I， 1992， 2（12）： 2221-2229.

［4］贾斌， 高自友， 李克平， 等. 基于元胞自动机的交通系统建模与模拟 ［M］. 北京： 科学出版社， 2007：70-97.

［5］谭惠丽， 刘慕仁， 孔令江. 开放边界条件下改进的Nagel-Schreckenberg交通流模型的研究 ［J］. 物理学报， 2002， 51（12）： 2713-2718.

TAN H L， LIU M R， KONG L J. A study on an improved nagel-schreckenberg traffic flow model with open boundary conditions ［J］. Acta Phys Sin， 2002， 51（12）： 2713-2718.

［6］TIAN J F， JIA B， LI X G， et al. A new car-following model considering velocity anticipation ［J］. Chinese Physics B， 2010， 19（1）： 197-203.

［7］NAGATANI T. Clustering of cars in cellular-automaton model of freeway traffic ［J］. J Phys Soc Jpn， 1993， 62（11）： 3837-3840.

［8］EMMERICH H， RANK E. An improved cellular automaton model for traffic flow simulation ［J］. Physica A， 1997， 234（3/4）： 676-686.

［9］DONG L Y， XUE Y， DAI S Q. One-dimensional cellular automaton model of traffic flow based on car-following idea ［J］. Appl Math Mech-Engl， 2002， 23（4）： 363-370.

［10］ LI L， YU X， DAI S Q. One-dimensional sensitive driving cellular automaton model for traffic flow ［J］. Acta Physica Sinica， 2003， 52（9）： 2121-2126.

［11］ RICKERT M， NAGEL K， SCHRECKENBERG M， et al. Two lane traffic simulations using cellular automata ［J］. Physica A， 1996， 231（4）： 534-550.

［12］ DAOUDIA A K， MOUSSA N. Numerical simulations of a three-lane traffic model using cellular automata ［J］. Chinese J Phys， 2003， 41（6）： 671-681.

［13］ KUKIDA S， TANIMOTO J， HAGISHIMA A. Analysis of the influence of lane changing on traffic-flow dynamics based on the cellular automaton model ［J］. International Journal of Modern Physics C， 2011， 22（3）： 271-281.

［14］ 敬明， 鄧卫， 王昊， 等. 基于跟车行为的双车道交通流元胞自动机模型 ［J］. 物理学报， 2012， 61（24）： 244502.

JING M， DENG W， WANG H， et al. Two-lane cellular automaton traffic model based on car following behavior ［J］. Acta Phys Sin， 2012， 61（24）： 244502.

［15］ ZHENG Z D. Recent developments and research needs in modeling lane changing ［J］. Transportation Research Part B-Methodological， 2014， 60（13）： 16-32.

［16］ LI H X， SHAO C F， WU H L， et al. Cellular automata approach for modeling lane changing execution ［J］. J Cell Autom， 2016， 11（4）： 339-350.

［17］ 邓建华， 冯焕焕， 葛婷. 多车道元胞自动机换道决策模型的冲突处理策略 ［J］. 交通运输系统工程与信息， 2019， 19（4）： 50-54.

DENG J H， FENG H H， GE T. Conflict handling strategies of lane-changing decision model of multi-lane cellular automata ［J］. Journal of Transportation Systems Engineering and Information Technology， 2019， 19（4）： 50-54.

［18］ WOLFRAM S. Universality and complexity in cellular automata ［J］. Physica D： Nonlinear Phenomena， 1984， 10（1）： 1-35.

［19］ PRODINGER H. On the analysis of an algorithm to generate a random cyclic permutation ［J］. Ars Combinatoria， 2002， 65（1）： 75-78.

［20］ DENG J H， FENG H H. A multilane cellular automaton multi-attribute lane-changing decision model ［J］. Physica A： Statistical Mechanics and its Applications， 2019， 529： 121545.

［21］ 邱小平， 于丹， 孙若晓， 等. 基于安全距离的元胞自动机交通流模型研究 ［J］. 交通运输系统工程与信息， 2015， 15（2）： 54-60.

QIU X P， YU D， SUN R X， et al. Cellular automata model based on safety distance ［J］. Journal of Transportation Systems Engineering and Information Technology， 2015， 15（2）： 54-60.

［22］ 梁经韵， 张莉莉， 栾悉道， 等. 多路段元胞自动机交通流模型 ［J］. 物理学报， 2017， 66（19）： 194501.

LIANG J Y， ZHANG L L， LUAN X D， et al. Multi-section cellular automata model of traffic flow ［J］. Acta Phys Sin， 2017， 66（19）： 194501.

［23］ 冯焕焕， 邓建华， 葛婷. 引入驾驶风格的熵权法多属性换道决策模型 ［J］. 交通运输系统工程与信息， 2020， 20（2）： 139-144.

FENG H H， DENG J H， GE T. Multi-attributes lane-changing decision model based on entropy weight with driving styles ［J］. Journal of Transportation Systems Engineering and Information Technology， 2020， 20（2）： 139-144.

（责任编辑 耿金花）