基于元胞自动机的行人和车辆疏散机理研究
姚层林 左传

摘要:近年来,城市经济水平飞速发展,对城市交通的发展起着支柱作用,使得城市交通设施不能完全与不断增加的汽车保有量相适应,城市交通问题日趋明显。路口人行横道处行人和车辆之间的相互干扰日益增强,以致整个路口的运行效率下降,此外,交通设施的不够完善从一定程度上造成了行人违规的不利后果,给行人和车辆带来巨大的安全隐患。因此,基于元胞自动机模型,深入了解行人和车辆的相互影响机理以及交通运行的特点,提出比较适合实际交通情况的建模方法,从而为有效地解决交通问题提供理论支持。
关键词:元胞自动机 交通路口 行人和车辆疏散
中图分类号:TP393 文献标识码:A 文章编号:1007-9416(2016)09-0054-02
1 引言
车辆组成的交通流是一个离散的系统,形成了复杂的交通运行状态。元胞自动机模型是交通流模型的基础,它定义在一个具有离散、有限状态的元胞组成的元胞空间上,并按照一定的局部规则,在离散的时间维度上随之演化,能够从微观角度分析复杂的交通模型。在元胞自动机中,某一时刻一个元胞的状态只与前一时刻此元胞以及相邻元胞的状态有关,能够将时间和空间离散化,分割成一个小小的单元,其特性与行人运动的特性较好地匹配。进而分析行人和车辆在路口的交通流演化准则,进行合理地分散,从而减少拥堵的发生。
2 城市道路拥堵
2.1 城市道路特点
城市交通多交叉路口,普遍由红绿灯控制,道路数量大,种类多。每条道路互连互通,交错纵横,形成网络,不同车辆的行驶情况导致了拥堵的必然发生。根据交通流量的不同,城市道路依次分为快速路、主干路、支路等层次。车流量较小时,车辆自由行驶,其间没有相互联系,当车流量超过临界值时,拥堵就会产生。
以武汉市王家湾路口为例(图1)。
2.2 交通拥堵
交通拥堵在实际道路上十分常见,一般来说,交通拥堵使车辆产生较长的排队现象,几乎无法前行。在拥堵和非拥堵的重合部分,交通流的状态非常不平稳,可能形成的自发拥堵也会影响交通的上游和下游,并由此向整个路网扩散。为了防止这类现象的发生,任何时候都需要加强对路口交通情况的处理。
3 基于元胞自动机的行人模型
根据元胞自动机的更新情况可分为:格子气体模型、领域模型[1]、Blue-Adler元胞自动机模型、动态参数模型等应用于行人流的仿真研究。
3.1 模型及演化规则
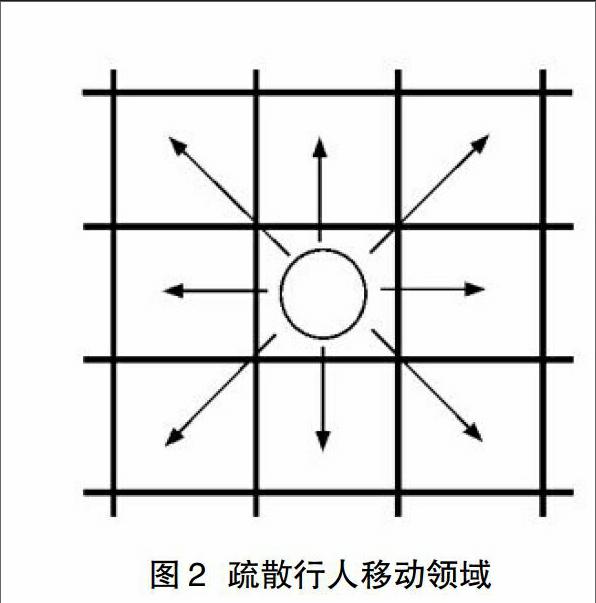
在二维离散元胞网格系统中,把行人的移动区域划分为大小相等的正方形网格,大小取0.4×0.4m,每个网格相当于一个元胞,空格分两种:被一个行人占据或为空。采用Moore邻居的模型,如图2所示,行人可以向8个方向运动或者选择原地等待,在每个离散的时间步长内,行人只能移动一个元胞的长度。模型演化过程中,多个行人会同时选择一个空格,该冲突使得模型以等概率随机确定一个行人的移动情况,没有被选择的保持静止。
3.2 行人运动特性
与车辆相比,行人运动更加复杂和不确定。根据环境的变化,他们会相应地选择恰当的方向和速度,而车辆受车道限制,相对来说运动特性比较简单[2]。行人只能近距离和低速行走,步行速度小,步行路线和位置的选择范围广,能够迅速补上一个空位元胞。正常情况下,行人步行的速度差别不大,最高速度与最低速度的差别可以忽略不计,并且行人从静止到运动的反应时间短,所以行人的运动特性可以认为只有静止或者以相同的速度前行。
3.3 行人元胞自动机模型
如图1所示的网格,路口处有较多行人,剩余绿灯时间不同,他们到达下一位置的时间不同,一般来讲,人行横道处剩余的绿灯时间越长,行人通过的速度就会越慢。通常来说,绿灯时间为10s以上时,行人平均速度为1.42m/s,10s内时间时,行人平均速度为1.84m/s[3],在网格上随机移动。当道路的行人流量≤1000人/小时,在行人间的相互干扰较小且外界因素作用不显著的情况下,服从泊松分布,如式1所示;而>1000人/小时,泊松分布不足以描述波动的人群,一般用负二项分布[4]来描述,如式2所示。
(1)行人尽量向前行;
(2)发生面对面的阻碍时,第一选择是向右移,右方有行人时,延时之后移到行人的位置内;
(3)两个行人之间的位置对他们而言,各有一半的概率互相占据。
在过街行人流较大的情况下,该模型有一种队列自动形成机制,体现行人的自动集中效应,提高道路的通行能力。
4 车辆模型
4.1 车辆位置
可以把任何车辆进入道路的事件看做一个随机的独立性事件。各车辆间的时间间隔可以视为一个随机量,在不同的时间区间内,车辆的流动是相互独立的。在一个很短的时间Δt内,区间[t,t+Δt]内车辆产生的概率与t无关,与Δt线性正相关。
4.2 车辆速度
根据车辆运行的特点,其速度一般服从对数正态分布或正态分布,可选择正态分布构建模型。
正态分布N(μ,σ2)的分布函数为:
F(X)=p(X≤x)=-∞ 当X服从N(0,1)时,Y=σX+μ服从N(μ,σ2),得到标准的N(0,1)正态分布的随机变量。使用Box-Muller的函数变换法则[5],产生两个均匀分布的随机数m1和m2,从而得出两个服从标准正态分布的随机变量n1和n2,表达式如下: n1=sin(2πm1) n2=cos(2πm2) 5 行人与车辆相互干扰模型 车辆与行人相互干扰的地点发生在人行横道,车辆通过人行横道时要根据行人的通过情况做出相应的反应。当人行横道无行人通过,车辆将其看做为空;当人行横道有行人通过,则车辆在靠近行人之前停止,直到行人完全穿过人行横道,则车辆视人行横道为被填充。
5.1 以车辆为主的红绿灯设置
绿灯时间步:人行横道入口处没有行人形走。如果人行横道处有人,则车辆在前面停止,若无行人,正常通过。
红灯时间步:未进入人行横道的车辆停止,刚进入人行横道的车辆尽快行驶,其余车辆的状态用VDR模型[6]表示。该模型中车辆减速的概率不是确定的函数,而是与车辆速度相关的函数:
f=f(v)=f0 if v=0;
f=f(v)=f if v>0 f0>f
由此看出,随机慢化规则是上一时刻时间步的速度确定下一时刻时间步的速度。
5.2 无红绿灯设置
与有红绿灯设置最大不同的是,人行横道入口处始终会有一定的概率出现行人,行人会根据车道第一辆车的位置和速度来判断是否能通过。根据t时刻车辆的位置情况和速度对车道第一辆车在(t+1)时刻的速度v(t+1)及位置做出预估,判断可能位置与人行横道的距离为d,在根据d与最大速度vmax的关系做出选择。若0
车辆避让模型
《中华人民共和国道路交通安全法》第四十七条规定[7]:机动车经过人行横道时,应当减速行驶;遇见行人正在通过人行横道时,应当减速行驶;遇见行人正在通过人行横道时,应当停车让行。
(1)加速过程:vr→min(vr+1,vmax-1),它对应的是车辆最大速度行驶的特性,车辆行驶达到最大速度不超过vmax-1。
(2)减速或停车:vr→min(vr,dr),车辆为了避免碰撞而选择减速或停车。
(3)随机慢化:以概率ps(0≤ps≤1),慢化有vr→max(vr-1,0),表示各种不确定因素导致的减速选项。
(4)位置变化;xr→xr+vr,表示车辆以变化后的速度行进。
xr、vr分别r车的位置和速度,dr=xr+1-xr=l表示r车和前车r+1之间空的元胞数量,l表示车辆的长度。
6 结语
(1)利用元胞自动机构建的模型,对经典交通路段(王家湾)的交通形式进行了分析。
(2)通过对行人和车辆的研究,得出相应的维持有序交通秩序的策略。
(3)城市交通受多种因素影响,交通拥堵的形成机理非常多变,本文基于一定的理想状况下进行的探讨,仍有许多不合理的问题没有考虑,如天气、街边路人等因素。
(4)已构建的交通模型适用范围比较不大,与实际情况的适应程度有待提高。
(5)以行人与车辆相互干扰模型为基础,可以考虑将行人违规对道路交通流产生的影响,根据行人的通行情况以及车辆追尾等因素的判断,从而更加全面地描述行人在复杂的路况下的特点。
参考文献:
[1]岳昊.基于元胞自动机的行人流仿真模型研究[D].北京:北京交通大学,2008:14-15.
[2]Burstedde C,Klauck K,Schadschneider A,et al.Simulation of pedestrian dynamics using a two-dimentional cellular automata moel[J].Chinese Science Bulletin,2001,29(5):507-525.
[3]冯树民,吴阅辛.信号控制交叉口行人过街速度分析[J].哈尔滨工业大学学报,2004,36(1):76-76
[4]王炜,过秀成等.交通工程学[M].南京:东南大学出版社,2003.
[5]孙亮.matlab语言与控制系统仿真[M].北京:北京工业大学出版社,2006.
[6]张笑梅.基于元胞自动机和模糊推理的交通流模型研究[D].大连理工大学,2013.
[7]《中华人民共和国道路交通安全法》.2003年,第四章第四十七条.

