基于三维元胞空间的多目标元胞遗传算法

祝勤友++许峰

摘 要：元胞遗传算法是一种将元胞自动机与遗传算法相结合的进化算法，这种算法具有遗传算法的适用性、并行性和扩展性，但是在后期的二维元胞空间扩散速度过慢。提出了一种基于三维球形元胞空间的多目标元胞遗传算法，其基本思想是：取元胞空间为三维球，根据Pareto支配关系找出种群中的非支配解并保存到精英集，根据元胞自动机中拓扑结构和邻居等机制，使精英集中的Pareto非支配解在种群中扩散。指标分析和数值实验表明，新算法的解不仅多样性和均匀性较好，而且在后期具有较快的扩散速度。

关键词：多目标遗传算法；元胞自动机；三维元胞空间；均匀性

DOIDOI：10.11907/rjdk.151598

中图分类号：TP312

文献标识码：A 文章编号文章编号：16727800（2015）009005204

0 引言

20世纪80年代初，著名物理学家Wolfram开始研究元胞自动机，他先后研究了一系列一维和二维元胞自动机，并根据研究成果，提出了著名的Wolfram规则。在此基础上，Wolfram 2002年出版了专著《A New of Science》。1987年，Robertson提出世界上第一个元胞遗传算法模型，该算法运行在CMI计算机上。此模型的所有遗传操作（父代个体的选择、替换、交叉和变异操作）都是并行执行。一年之后，Muhienbein等发表了一篇利用运行在大规模并行机器上的元胞遗传算法求解TSP问题的文章，该算法添加了一个局部搜索，改善了由交叉和变异算子产生的解。因此，该算法被认为是第一个混合元胞遗传算法。之后，又出现了一些元胞遗传算法。它们被称为Pollination plants、Parallel individual、Diffusion、Fine grained、Massively parallelm模型。

鉴于元胞遗传算法对于搜索空间能够带来全局搜索和局部寻优的良好平衡，具有优越的复杂问题解决能力，许多学者将其用于解决实际工程问题中，主要应用领域有：神经网络训练、电子信息、机械设计制造、调度决策问题数学优化、交通控制、3D动画设计、图像处理、经济学、生物学等。

本文根据元胞遗传算法操作特点，对遗传算法的元胞空间进行分析，提出一种基于三维元胞空间的多目标元胞遗传算法，并对该算法进行性能分析和数值实验。

1 元胞遗传算法与元胞空间

1.1 元胞遗传算法

元胞遗传算法（Cellular Genetic Algorithms， CGA）是一种将遗传算法和元胞自动机原理相结合的进化算法。在元胞遗传算法中，元胞模型从初始个体出发对自然界的进化过程进行模拟，初始种群被分布在一个相互联通的平面或空间拓扑结构中，在这种相互联通的网状结构中，个体被安放在网格点上，每个个体只能与其邻近的个体进行信息交换，而且交叉操作也被严格限制在邻近个体间进行。这样，可以使得种群中的个体产生一定的隔离，类似于自然界中的小生境，从而保持种群的多样性。

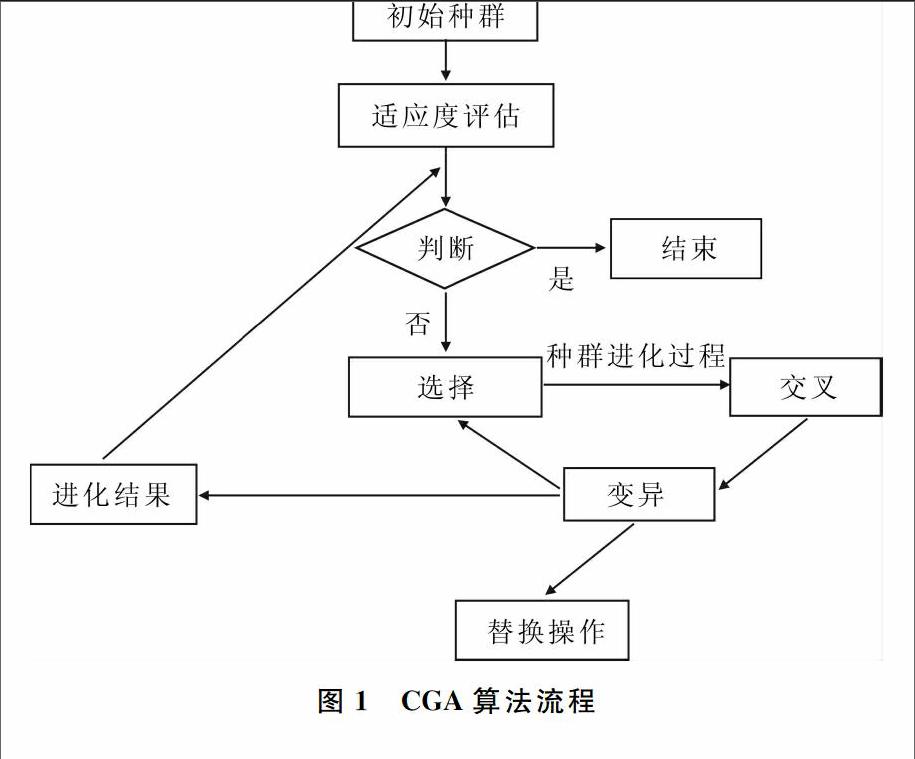
CGA算法流程见图1。

图1 CGA算法流程

1.2 元胞空间

在元胞自动机中，空间和时间都是离散的，物理量只取有限值集。元胞自动机由元胞、元胞空间、邻居和规则这4个基本部分组成。许多对元胞遗传算法的改进多集中于对元胞自动机各组成部分的改进，本文主要对元胞空间进行改进。

元胞所分布的空间网点的集合称为元胞空间，可以按照几何开关、边界条件对元胞空间进行分类。目前，元胞遗传算法多采用一维和二维元胞空间。对于一维元胞自动机，元胞空间的划分只有一种。而高维的元胞自动机，元胞空间的划分可有多种形式。在二维元胞自动机中，三角形、四边形和六边形元胞空间最为常见，见图2。

图2 四边形、三角形、六边形元胞空间

三维元胞空间可以是多种形状，考虑到网格点的均匀分布，本文采用三维球形元胞空间，见图3。

图3 三维球形元胞空间

2 多目标元胞遗传算法

考虑到元胞遗传算法的优良特性，Alba于2007年提出了第一个元胞多目标遗传算法cMOGA。之后，Alba又对其进行了改进，给出了改进的cMOGA，即MOCell。Durillo将广义差分算法引入MOCell算法，提出了一种混合元胞多目标遗传算法CellDE，大大提升了MOCell解决三目标问题的效果，此算法在解决三目标问题时明显优于NSGAII和MOCell。Li等提出了一种自适应元胞多目标遗传算法，使得算法的收敛速度在一定程度上得到了提高。张屹等在CellDE中添加了一个变异算子，提出了新的差分进化多目标元胞算法 DECell，有效地保持了种群多样性，增大了解集的覆盖范围。

2.1 多目标遗传算法

多目标优化问题的数学模型为

双目标优化问题的Pareto最优前沿通常是平面曲线，而三目标优化问题的Pareto最优前沿往往是空间曲面。

2.2 最优解集评价标准

对多目标优化算法性能的评价包括算法的运行效率和最优解集的质量。算法的运行效率主要指算法的复杂性，可以用算法占用的CPU时间表示，最优解集的质量包括算法的全局、局部收敛性和最优解集的均匀性、分布性。目前，评价多目标优化算法性能主要依靠典型测试问题的数值实验和量化评价指标值，本文采用的量化评价指标值如下：

（1）代间距离（Generation Distance， GD）：

其中，n和di与（1）中相同。实际上，SP就是di的标准差。根据标准差的意义，SP描述的是最优解集的均匀性。

2.3 多目标三维元胞空间遗传算法

在CGA中，遗传算法将初始种群均匀地分布在元胞空间拓扑结构中。在这种元胞空间的网状结构中，每个个体被置于网格点上，每个个体只能与其邻近个体交叉操作。元胞遗传算法最主要的优点在于，在对解空间进行搜索时，能保持全局搜索和局部寻优平衡。但是在这种平衡下，后期的最优解在种群中扩散的速度比较缓慢，效率不高，这时候算法的繁殖周期较大，即最优个体占据元胞空间所需要的周期比较长。

为了改善后期效率，可以对元胞空间进行改进，将初始种群中的个体安置于三维元胞空间中。类似于二维元胞空间，将初始种群均匀分布在球体的表面网格中，这种网状结构的边界是同心球球面，一个个体的邻居是根据它在种群网格中与其它个体之间的距离（二个同心球的半径距离）来定义的。对于二维元胞空间遗传算法，个体与自己的邻居进行进化产生的新个体，繁殖的周期一致，但是当繁殖周期到一定程度时，原先的元胞遗传算法会出现种群中最优个体扩散到窄边界的情况，这时候最优个体扩散速度明显下降。但是在三维元胞空间中，种群分布在球的表面，不会出现上述情况，这时最优个体所占比例增长速度不会出现变慢的现象。

算法流程如下：①将初始种群分布在三维元胞空间中；②在相邻的元胞中选择一个个体作为父代；③将选择出来的邻居元胞与中心元胞进行交叉，变异操作；④根据Pareto支配关系找出种群中的非支配解并保存到精英集中，产生新的个体；⑤如果产生的新个体优于中心元胞，则将中心元胞替换，否则，不替换；⑥如果代数小于最大进化代数，则返回到步骤②；⑦将当前最优解输出。

3 数值实验

为了检验算法性能，下面对两个多目标进化算法标准测试函数DTLZ1和DTLZ2进行数值计算，并将优化结果与普通多目标元胞遗传算法的优化结果进行比较。

数值实验参数是：群体规模为200，进化代数为200，交叉概率为0.85，变异概率为0.1。

从表1和表2可以看出，基于三维元胞空间的多目标元胞遗传算法的GD指标明显优于常规CGA算法，表明引入三维元胞空间的确明显改善了CGA的全局收敛性。三维CGA的ER和SP指标较常规CGA算法也显著占优，表明三维CGA解的分布性和均匀性也有明显提高。

由此得出明确结论：基于三维元胞空间的多目标元胞遗传算法与二维多目标遗传算法相比，在解的分布性、均匀性和收敛性方面有明显改善。

4 结语

针对二维元胞遗传算法后期解的扩散速度较慢这个缺陷，将三维球形元胞空间引入多目标元胞遗传算法。指标分析与数值实验结果表明：三维多目标元胞遗产算法在后期的扩散速度较快，解的分布性、均匀性、收敛性均明显优于二维多目标元胞遗传算法。

目前，遗传算法、多目标进化算法、元胞遗传算法的理论基础还很薄弱，性能研究只能依赖于对测试问题的对比实验。元胞遗传算法的收敛性及解的性能等有待进一步研究。

参考文献参考文献：

[ 1 ] WOLFRAM S. A new kind of science[ M ].Champsign： Wolfram Media， 2002.

[ 2 ] ROBERTSON G. Parallel implementation of genetic algorithms in a classifier system[ C ].Proceedings of the Second International Conference on Genetic Algorithms， New Jersey， 1987： 140147.

[ 3 ] MUHLENBEIN H，GORGES SCHLEUTR M，KRAMER O.Evolution algorithms in combinatorial optimization[ J ].Parallel Computing， 1988（7）： 6588.

[ 4 ] GOLDBERG D E.Genetic algorithms in search，optimization and machine learning[ M ].Reading：AddisonWesley，1989.

[ 5 ] HOFFNEISTER F.Applied parallel and distributed optimization[ M ].Heidelberg：SpringerVerlag，1991.

[ 6 ] BACKT，FOGEL D B，MICHALEWICZ Z.Handbook of evolutionary computation[ M ].London：Oxford university press， 1997.

[ 7 ] MANDERICK B，SPIESSENS P.Finegrained parallel genetic algorithms[ C ].Proceedings of the Third International Conference on Genetic Algorithms，Richmond，1989：428433.

[ 8 ] HILIS D.Coevolving parasites improve simulated evolution ad an optimizing procedure[ J ].Physical D，1990（42）：228234.

[ 9 ] ALBA E，DORRONSORO B，LUNA F.A cellular multiobjective genetic altorithm for optimal broadcasting strategy in metrolitan MANETs[ J ]. Computer Communications， 2007， 30（4）： 685697.

[ 10 ] NEBRO A J，DURILLO J J，LUNA F.MOCell：a celluar genetic algorithm for multiobjective optimization[ J ].International journal of Intelligent Syetems， 2009， 24（7）： 726746.

[ 11 ] DURILLO J J，NEBRO A J，LUNA F.Solving threeobjective optimization problems using a new hybrid cellular genetic algorithm[ C ].Proceedings of the International Conference on Parallel problem Solving from Nature. Heidellberg： SpringerVerlag， 2008： 661670.

[ 12 ] LI X Y，SUN Y F，LIU C Y.The adaptive cellular genetic algorithm and analysis of stock prices[ J ].Journal of Wuyi University，2011，25（4）：5765.

[ 13 ] 张屹，卢超，张虎.基于差分元胞多目标遗传算法的车间布局优化[ J ].计算机集成制造系统， 2013， 19（4）： 727734.

责任编辑（责任编辑：杜能钢）