基于COVID-19传播特性的传染病模型的构建与研究

朱懋昌 宾晟 孙更新

摘要： 为了更好地揭示新冠肺炎（COVID-19）的传播机理，通过分析新冠病毒（2019-nCoV）的传播特性，考虑隐性潜伏者的自愈以及潜伏者的提前隔离，引入“入院隔离状态”，“隐性治愈状态”，考虑防控强度的变化，引入“发病状态”，提出了SEAIHR动力学模型。利用真实疫情数据，考虑不同阶段参数的变化，进行了多模型对比试验。实验结果表明，SEAIHR模型拟合和预测精度有明显提升，较经典模型在疫情前中期降低了34.4%～72.8%拟合误差，为疫情防控提供了参考与指导。

关键词： SEIR；隐性潜伏者；COVID-19；动力学模型

中图分类号： O29;TP391文献标识码： A

收稿日期： 2022-04-27；修回日期：2022-07-22

基金项目： 山东省自然基金面上项目（ZR2021MG006）；山东省社会科学规划项目（17CHLJ16）

第一作者： 朱懋昌（1997-），男，山东济宁人，硕士研究生，主要研究方向为复杂网络。

通信作者： 孙更新（1978-），男，山东青岛人，博士，副教授，主要研究方向为复杂网络，复杂网络中传播动力学及相关传播模型。

Construction and Research of Infectious Disease Model Based on COVID-19 Transmission Characteristics

ZHU Maochang， BIN Sheng， SUN Gengxin

（School of Computer Science and Technology， Qingdao University， Qingdao 266071， China）

Abstract：In order to better reveal the transmission mechanism of COVID-19， this paper proposes the SEAIHR dynamic model by analyzing the transmission characteristics of COVID-19， considering the self-healing of the hidden lurks and the early isolation of the lurks， introducing “h hospitalization isolation”， “recessive cure”， considering the change of prevention and control intensity， and introducing “morbidity status”. Using the real epidemic data and considering the changes of parameters in different stages， a multi model comparative test was conducted. The experimental results showed that the fitting and prediction accuracy of the SEAIHR model was significantly improved， and the fitting error was 34.4%～72.8% lower than that of the classical model in the early and middle stages of the epidemic， providing reference and guidance for epidemic prevention and control.

Key words： SEIR；hidden lurker； COVID-19； dynamic model

0 引言

自新冠肺炎第一例病例出现，几十天内迅速蔓延至全国各地。截至2021年9月24日，全国累计报告新型冠状肺炎（COVID-19）确诊病例124 403人，且该数据仍在持续增加。研究表明，新型冠状病毒不仅具有较长的潜伏期而且潜伏期内存在传染性，同时在其传播过程中存在隐性潜伏者，即潜伏期后无症状且仍具备传染性的群体。现阶段中国的防疫工作取得了巨大的成果，但国内疫情反弹的风险始终存在。因此，结合新冠肺炎的传播特点和后疫情时代的常态化防控措施，建立一个能准确描述新冠病毒传播机理的传播模型十分必要。

自COVID-19爆发以来，研究人员做了大量相关研究，文献［1］提出了一种SIRU模型，该模型首次提出未报告的有症状病例的数量，并且在不同等级的防控措施下预测疾病传播趋势；LI Qun等［2］根据最早425例确诊病例数据，估计了关键流行病学延迟时间分布情况、传染病倍增时间以及基本再生数；耿辉等［3］建立了包含潜伏期传染性的SEIR模型，估算了基本再生数；范如国等［4］基于SEIR模型考虑了多种病毒潜伏期情景，分别进行了拐点的预测；文献［5］考虑了数据滞后性，建立了基于时滞动力学的传播模型，对疫情的发展进行了预测；Nursanti Anggriani等［6］考虑了有症状和无症状的状态以及免疫力下降，建立了一个包含7个仓室的传播模型。现有传染病传播模型大多基于SIR［7］、SEIR［8］等经典模型进行改进：曹力盛等［9］基于SEIR模型充分考虑了隔离措施对于疫情的遏制作用，利用欧拉数值方法对模型进行求解，对疫情进行评估和预测。文献［10］利用長短期记忆算法（LSTM）提出一种mSEIR模型，采用滑动窗口算法进行参数估计和人口预测。Denis Efimov等［11］在传统SEIR模型的基础上分离出治愈者与病死者，考虑模型参数的变化和不确定性，分析了8个不同地区的疫情发展趋势。林俊峰［12］基于SEIR模型重新定义了潜伏者与感染者，并引入了隐形传播者。邓春燕等［13］提出一种D-SEIR模型，考虑了地区间与地区内的人口流动情况。廖影等［14］根据乌鲁木齐市的真实疫情数据建立仓室模型，利用非线性最小二乘法拟合参数。除此之外，荆磊等［15］构建了一种基于SEIRD-GEOCA的传染病时空耦合模型，并在模型中融入了蔓延扩散和随机迁移扩散策略用来模拟COVID-19疫情的时空扩散规律。He S等［16］采用粒子群优化算法（PSO）对系统参数进行估计，研究发现对于不同的场景，所提出的SEIR模型的参数是不同的。Annas S等［17］建立了以疫苗接种和隔离因子为模型参数的SEIR模型，采用生成矩阵法获得2019冠状病毒疾病分布模型的基本繁殖数和全局稳定性。Liu C等［18］使用集合经验模态分解（EEMD）模型和自回归-移动平均（ARMA）模型对GPCP的预测结果进行改进，并对GPCP模型无法预测的国家进行直接预测。文献［19］利用改进的SEIR模型和关键驱动协变量（肺炎季节性、流动性、检测率和人均面罩使用）的预测，评估了社会距离要求和面罩使用水平的情景。

上述研究中模型的参数大多是固定不变的，并且随着疫情的变化，模型的适用性逐渐变弱。针对现有研究的不足，本文通过控制参数变化来增加模型的鲁棒性并且根据实际防控措施细化模型，从3个方面进行模型的改进，以更加准确地分析疫情的演化过程：

1）考虑COVID-19中存在的隐性潜伏者以及其传染性，建立“隐性治愈者”仓室，便于模拟和分析此类人群在疫情发展过程中的影响；2）考虑疫情防控对潜伏者的提前隔离，针对隐形潜伏者和显性潜伏者建立“入院隔离”仓室；3）考虑模型参数的时变特性，将治愈率和死亡率设置为日变化参数，感染率等参数考虑阶段性变化。

1 面向COVID-19的传播动力学模型

1.1 SEIR模型

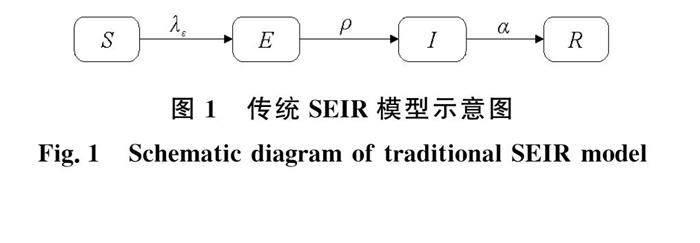
传统SEIR模型把人群分成4类：易感者、潜伏者、感染者、移出者。其中，易感者（S）表示未被感染的健康人群，接触感染者可被感染；潛伏者（E）表示未出现症状但感染了病毒的人群，此类人群病毒尚未发作，不具有传染性；感染者（I）表示出现症状并且具有传染性的人群，此类人群可以通过接触将病毒传染给易感者；移出者（R）表示被治愈的感染者或者死亡的人群，治愈后的人群具有抗体不会被再次感染。图1展示了SEIR模型各状态之间的转换。图1中，S，E，I，R分别为易感者、潜伏者、感染者、移出者的人数；λ为感染者每一时刻平均接触到的人数；ε为易感者占总人数的比例；ρ为每一时刻转化为感染者的比例；α为感染者转化为移出者的概率。

1.2 基于COVID-19传播特性及防控措施的模型构建

本研究基于经典SEIR模型建立更加符合COVID-19实际传播特性的SEAIHR模型。新冠肺炎传播特点：1）新型冠状病毒存在潜伏期，潜伏期内无明显症状且具有传染性；2）潜伏者中存在一定数量的隐性潜伏者，该人群潜伏期后无症状但具备传染性，经发病周期后自愈;3）随着疫情防控的进展，潜伏者在发病前可被检测入院隔离治疗。

结合上述疫情传播特点，建立8个仓室：易感者、显性潜伏者、隐形潜伏者、发病者、入院隔离者、隐形治愈者、治愈者、病死者。根据疫情实际传播情况，本文所建立模型基于假设：1）疫情期间封城，不考虑人口流动；2）所有入院治疗的感染者被隔离，不具有传染性；3）忽略病毒传播期间人口的自然死亡及自然出生。

为了简化模型，本研究认为发病人群在入院前会进行自我防护，忽略其传染性。在上述仓室中：易感者（S）是指容易被感染的健康人群；显性潜伏者（E）是指经过潜伏期后有症状且具备传染性的人群；隐性潜伏者（A）是指感染者经过潜伏期后无症状且仍具备传染性的人群；隐性治愈者（C）是指隐性潜伏者经发病周期后自愈的群体，这部分群体未表现出明显症状，不算在官方公布的治愈病例中；发病者（I）是指潜伏者经过潜伏期后发病暂时未入院的人群；入院隔离者（H）是指被隔离治疗不具备传染性的人群；治愈者（R）是指入院隔离后被治愈的人群；病死者（D）是指入院隔离后病死的人群。基于上述8个仓室，构建不同仓室之间的状态转移关系，如图2所示。

各状态之间的转换规则为：1）易感人群（S）以一定概率被潜伏者感染，转化为显性潜伏者（E）和隐性潜伏者（A）；2）潜伏者在疫情前期未被及时追踪隔离，隐性潜伏者（A）转化为隐形治愈者（C），而显性潜伏者（E）发病后入院隔离治疗;3）疫情中后期，显性潜伏者（E）和隐性潜伏者（A）被追踪隔离入院，直接转化为入院隔离者（H），通过隔离治疗转化为治愈者（R）或病死者（D），当人群处于治愈状态或病死状态后，其状态不再发生改变。基于上述状态间转移规则及系统动力学，SEAIHR模型的动力学方程如式（1）所示。

dStdt=-Etλ1+Atλ2dEtdt=1-mEtλ1+Aλ2-Etβ1-EtμdAtdt=mEtλ1+Atλ2-Atβ3-Atβ2dItdt=Eμ-IρdHtdt=Etβ1+Iρ-HPr+PddCtdt=Atβ3dRtdt=HPrdDtdt=HPd（1）

其中，St，Et，At，It，Ht，Ct，Rt，Dt分别为t时刻易感者、显性潜伏者、隐性潜伏者、发病者、入院隔离者、累计隐形治愈者、累计治愈者、累计病死者的人数。

本文所建动力学模型共包含10个参数，一部分可以通过估算或者官方数据确定，这类参数为直接参数；另一部分无法直接获取或者估算，这类参数为间接参数，间接参数采用参数反演拟合其最优值。各参数解释如表1所示。

在已知{β1，β2，β3，μ，m}值的情况下，{λ1，λ2，ρ}的最优值可通过求解式（2）得到，优化目标为实际数据与模拟数据的偏差：

minλ1，λ2，pHλ1，λ2，ρ，t-H数据t2+Rλ1，λ2，ρ，t-R数据t2+Dλ1，λ2，ρ，t-D数据t2（2）

本文将治愈率和死亡率视为日变化的参数，Pr和Pd分别表示日治愈率和日死亡率，其值为当日新增治愈人数和新增死亡人数占前一天入院隔离人数的比例。本文使用非线性最小二乘法进行拟合，即通过求解式（3）的局部最小值进行参数求解，拟合方程使用幂函数。

Fx=12∑y1x-y22（3）

其中，y1x为要拟合的目标函数值，y2为实际数值。找到最优的自变量x，让每个点y1x-y2的残差平方之和最小，从而得出拟合曲线。去除2020年2月12日及2月13日两天波动较大的时间点，拟合结果如表2所示。

武汉市的治愈率和死亡率表现出随时间变化的趋势，将其设置为时变参数以更准确地模拟疫情发展的真实情况，拟合结果如图3和图4所示。

1.3 模型精度指标

模型计算结果与真实疫情数据比较，以验证模型的准确性。因此，本文使用拟合数据与入院确诊病例人数的均方根误差（RMSE）和平均相对误差（MAPE）作为模型精度指标，表达式如式（4）和（5）所示。

RMSE= 1t∑ti=1Ht-Rt2（4）

MAPE=100%t∑ti=1Rt-HtRt（5）

其中，R（t）为真实数据的入院隔离人数，H（t）为模型拟合入院人数，RMSE和MAPE的值越小，说明拟合结果和真实数据越接近，模型的拟合和预测精确度越高，模拟效果越好。

2 实验结果与分析

2.1 武汉市疫情回溯

本研究根据武汉市卫生健康委员会官网（http：//wjw.wuhan.gov.cn/）公布的武汉市2020年1月22日～2020年4月26日的疫情数据进行实验。基于SIR模型、SEIR模型与SEAIHR模型进行了仿真对比，以验证SEAIHR模型的优越性。2020年2月12日武汉市第1次通报疑似病例，说明此时武汉市医疗能力已经可以追踪到大部分隐性潜伏者，且各地开始出现无症状感染者的相关报道。2020年2月26日起新增确诊人数显著下降，治愈病例显著上升。直至2020年4月27日，现存确诊人数清零。综上所述，本文实验将分为3个阶段：1）2020年1月22日～2月11日，疫情爆发期;2）2020年2月12日～2月26日，疫情有效控制期;3）2020年2月26日～4月27日，疫情衰退期。

2.1.1 武汉市疫情第1阶段拟合结果分析

疫情初期官方公布的数据中并未包括潜伏者数量以及发病者人数，本文根据文献［20］和文献［21］指出的潜伏期区间与发病到入院时间，迭代反推出潜伏者和发病者初始值，其中隐性潜伏者比例根据其占潜伏者总数的平均比例设置m值。

武汉市2020年1月22日至2月11日的拟合结果如图5所示。结果显示：3种模型在疫情初始阶段均呈现加速上升趋势，但SIR模型和SEIR模型的上升趋势远超过真实疫情的发展，SEAIHR模型整体拟合趋势较好。根据表3的评价结果，SEAIHR模型的拟合精度有较为显著的提升。其中，均方根误差值（RMSE）比SIR模型缩小了59%，比SEIR模型缩小了53%，平均相对误差值（MAPE）比SIR模型缩小了37.3%，比SEIR模型缩小了34.4%。

表4所示第1阶段各参数值中，两类潜伏者感染率分别为0.491和0.433，λ1值略高于λ2。这说明由于疫情早期对于病毒的了解和医疗能力有限且收治压力巨大，使得潜伏者在人群中自由传播，其中隐性潜伏者的病毒载量低于显性潜伏者，此时疫情处于迅速爆发期。同时，由于检测手段和追踪能力严重不足，导致隐性潜伏者自愈未计入官方数据，显性潜伏者均发病后入院。而因疫情前期的医疗容量有限，发病入院率仅为0.09，说明从发病到入院有较长的一段时间延迟，进一步造成了治愈率较低和死亡率较高的结果。

根据文献［22］和［23］中给出的关于基本再生数计算方法，分别计算了疫情爆发初期本文模型与实际数据基本再生数的值，表达式如式（6）和（7）。

RSEAIHR=max（λ1，λ2）Pr+Pd+β1+β3（6）

RActually=1+rTL1+rSI-TL（7）

式（7）假定被感染人数呈指数增长，其中，r为指数增长的增长率，TL为被感染者的潜伏期的平均長度，SI为一个感染者与他感染的下一个人的发病时间间隔。根据实际情况估算令TL为7，SI-TL为2，计算得出实际数据的基本再生数为3.215。由于本文假设忽略自然出生率及死亡率，并且将治愈率和死亡率设置为时变参数，根据式（6）计算出本文模型第1阶段的基本再生数区间为〈2.889，3.151〉，说明此时疫情处于快速上升期。SEAIHR模型与实际数据计算出的基本再生数误差为5%左右。

2.1.2 武汉市疫情第2阶段拟合结果分析

自2020年2月12日，武汉市开始统计疑似病例，说明此时武汉市已经可以追踪大部分潜伏者，同时定点医院由2家增加到48家，新建方舱医院16家，初步实现了应收尽收，疫情发展趋势将出现拐点。第2阶段的模拟结果如图6和图7所示，显性潜伏者人数减少了70%，隐性潜伏者人数降低到143人，此时的基本再生数区间为〈0.444，0.486〉，说明随着追踪隔离强度的增加与民众自我防护意识的增强有效控制了疫情扩散，同时SEAIHR模型准确地复现了2020年2月12日至2020年2月26日武汉疫情的拐点以及衰退趋势。

武汉市疫情第2阶段参数值如表5所示，显性潜伏者和隐性潜伏者的感染率较第1阶段减小了89.4%、81.1%，潜伏者入院隔离率由0提高到0.111，换算成天数为9 d，同时发病率较第1阶段降低了92.5%，发病入院时间比第1阶段快了4.1 d，说明政府干预和积极的防控措施对疫情的控制产生了巨大的效果。

表6显示，SEAIHR模型相比于SIR模型的RMSE值、MAPE值分别缩小了52.6%，52.8%，比SEIR模型的RMSE值、MAPE值分别缩小了73.6%，76.8%，充分体现了SEAIHR模型的合理性和准确性。

2.1.3 武汉市疫情第3阶段拟合结果分析

2020年2月18日现存确诊病例到达峰值，随着疫情拐点的到来，疫情逐渐呈现衰退趋势。观察表7，隐性潜伏者感染率和发病率接近于0，发病入院速率提升了38.9%。图8模拟了武汉市疫情的第3阶段，可以看出SEAIHR模型与SEIR模型对于真实数据的拟合较为准确，这是因为随着防控强度的上升和医疗检测手段的完善，SEAIHR模型可以近似为传统SEIR模型。根据表8，SEAIHR模型对比经典模型依旧有一定程度的提升。均方根误差较SIR和SEIR模型分别提升22.6%和29.8%，平均相对误差较SIR和SEIR模型分别提升22.8%和13.3%。此时的基本再生数区间为〈0.114，0.177〉。

本研究实验采用阶段性拟合方法，结果显示：SEAIHR模型较经典模型显著提升了模拟精度，准确复现了疫情爆发到衰退的趋势以及疫情拐点出现的时间节点。而由于疫情衰退期潜伏者被及时追踪隔离以及发病入院率的提升，此时本文模型与经典SEIR模型近似。此外，SEAIHR模型挖掘出了官方未统计到的数据，如隐性潜伏者人数、显性潜伏者人数、隐性治愈者人数等，揭示了影响疫情发展的潜在因素。

2.2 新疆疫情传播趋势预测

2.1节利用SEAIHR模型对武汉疫情发展进行了回溯，验证了模型对于历史数据的拟合、揭示疫情发展机理的准确性。在本小节中，为了进一步验证SEAIHR模型对于预测常态化防控下疫情发展的准确性，利用新疆卫健委官网从2020年7月16日至8月27日公布的疫情数据进行实验，实验分为模型参数确定及疫情发展预测两部分。基于SIR模型、SEIR模型与SEAIHR模型进行仿真对比实验，以验证本文模型预测疫情发展的性能。

2.2.1 数据拟合与参数确定

由于武汉疫情的防控经验，新疆疫情伊始即进入了人为强干预的控制状态，自2020年7月16日出现首个病例至7月29日出现第1例治愈病例，针对新疆疫情实际防控措施进行模型的参数拟合。本研究将治愈率视为时变参数，使用2020年7月16日至8月27日的数据进行拟合并代入模型。治愈率拟合结果如图9所示。

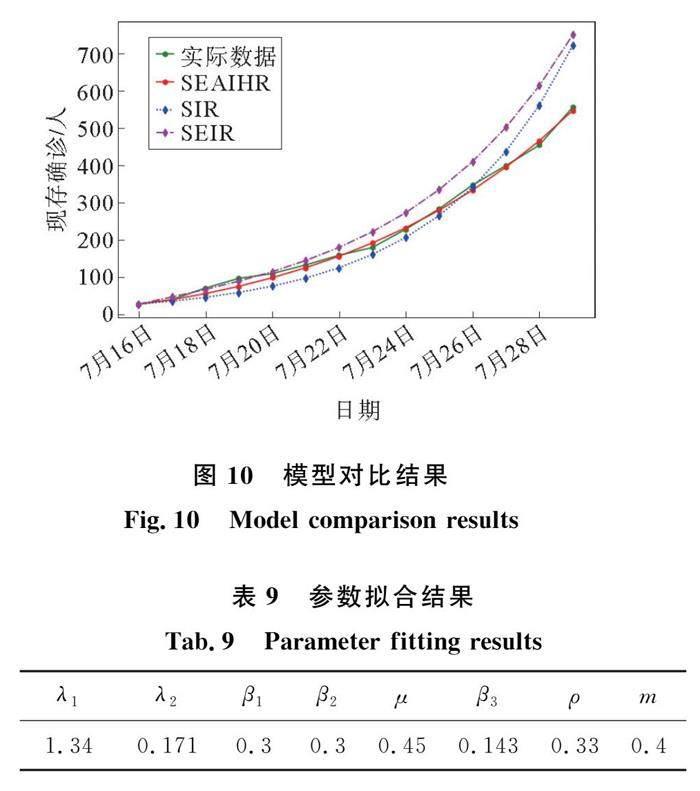
图10显示，SEAIHR模型对于真实数据的拟合更为准确，拟合误差仅为3.1%。相较于SIR和SEIR模型准确地模拟了疫情发展与现存病例人数的变化。观察表9，其中λ2值仅为λ1的12.7%，说明政府的干预措施起到了重要作用，使隐性潜伏者的传染风险大大降低。但由于病毒存在潜伏期，可疑人群的流调溯源存在时滞效应，导致潜伏者在发病之前已经在人群中自由传播了一段时间，现存确诊人数在初始的两周呈上升趋势。

2.2.2 疫情预测

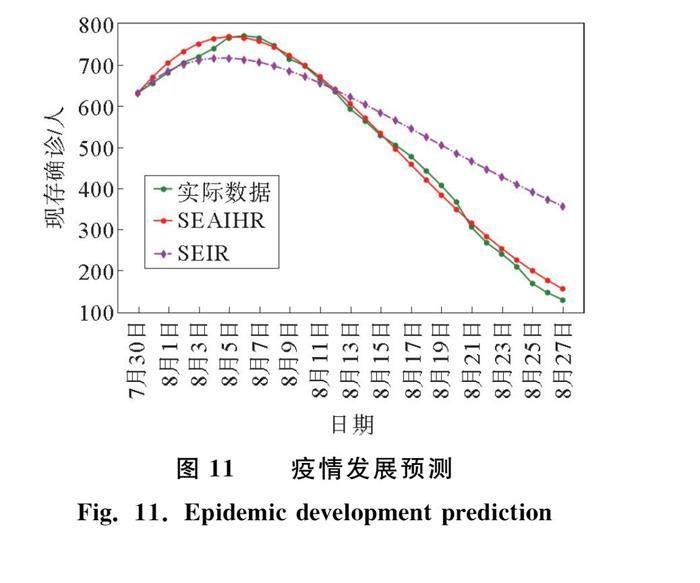
上一小节通过使用新疆疫情的实际数据确定了模型参数的取值，接下来结合实际防控措施对未来四周的疫情发展进行预测。实验预测结果如图11所示，疫情拐点出现在8月6日左右，现存确诊人数在此时达到峰值，峰值在771人左右。这说明，政府的各项防控举措在较短时间内控制住了局部疫情的爆发，相较于武汉疫情，新疆仅用了20 d左右的时间将疫情控制，入院确诊人数不超过800人。从图11中可以看出，现存确诊人数在8月末被控制在150人以内，标志着疫情基本稳定。由图11可以看出，SEAIHR模型相较于SIER模型更为准确地预测了拐点出现时间以及疫情衰退趋势。表10列出了模型预测结果与官方实际数据，可以看出实验预测的峰值出现时间节点和数值与官方统计数据较为吻合。

3 结论

本文结合病毒最新的传播特点以及不同的防控措施，充分考虑了各个阶段状态转移参数的变化，提出了一种包含“易感者，隐性潜伏者，显性潜伏者，入院隔离者”等8类状态的传染病传播模型。利用武汉市与新疆的真实疫情数据进行了拟合和预测实验。实验表明：对于COVID-19历史传播数据，SEAIHR模型具有更高的拟合精度，对于武汉疫情前中期的拟合误差较经典模型降低了34.4%～72.8%，更准确地模拟了疫情发展趋势以及拐点的时间；SEAIHR模型能够准确地描述在病毒传播过程中不同的疫情防控强度对于疫情发展的影响，同时可以根据实际防控措施对疫情发展进行预测；SEAIHR模型可以挖掘疫情传播中难以发现的隐藏数据，更深刻地刻画了疫情传播过程中的不同群体与传播机理。总之，本文研究为COVID-19及类似传染病的防控提供了参考与指导。

参考文献：

［1］LIU Z H， MAGAL P， SEYDI O， et al. Understanding unreported cases in the COVID-19 epidemic outbreak in Wuhan， China， and the importance of major public health interventions［J］. Biology，2020，9（3）： 50.

［2］LI Q， GUAN X， WU P， et al. Early transmission dynamics in Wuhan， China， of novel coronavirus-infected pneumonia［J］. New England journal of medicine， 2020，382（13）： 1199-1209.

［3］耿輝， 徐安定， 王晓艳， 等. 基于 SEIR 模型分析相关干预措施在新型冠状病毒肺炎疫情中的作用［J］. 暨南大学学报 （自然科学与医学版）， 2020， 41（2）： 1-7.

GENG H， XU A D， WANG X Y， et al. Analysis of the role of related interventions in new coronavirus pneumonia based on SEIR model ［J］. Journal of Jinan University （Natural Science and medicine）， 2020， 41 （2）： 1-7.

［4］范如国，王奕博，罗明，等. 基于SEIR的新冠肺炎传播模型及拐点预测分析［J］. 电子科技大学学报，2020，49（3）：369-374.

FAN R G， WANG Y B， LUO M， et al. A novel coronavirus pneumonia transmission model and inflection point prediction based on SEIR ［J］. University of Electronic Science and technology， 2020，49（3）：369-374.

［5］严阅，陈瑜，刘可伋，等.基于一类时滞动力学系统对新型冠状病毒肺炎疫情的建模和预测［J］. 中国科学：数学，2020，50（3）：385-392.

YAN Y， CHEN Y， LIU K Z， et al. Modeling and prediction of new coronavirus pneumonia based on a class of delayed dynamical systems ［J］. China Science： Mathematics， 2020，50 （3）： 385-392.

［6］ANGGRIANI N， NDII M Z， AMELIA R， et al. Amathematical COVID-19 model considering asymptomatic and symptoma-tic classes with waning immunity［J］. Alexandria Engineering Journal， 2022， 61（1）： 113-124.

［7］KERMACK W O， MCKENDIRCK A G. Contributions to the mathematical theory of epidemics-I. 1927［J］. Bulletin of mathematical biology， 1991， 53（1/2） ： 33-55.

［8］Anderson R M，  May R M. Infectious Diseases of Humans： Dynamics and Control［M］. Oxford： Oxford University Press，1991：99.

［9］曹盛力， 冯沛华， 时朋朋. 修正 SEIR 传染病动力学模型应用于湖北省 2019 冠状病毒病 （COVID-19） 疫情预测和评估［J］. 浙江大学学报 （医学版）， 2020， 49（2）： 178-184.

CAO S L， FENG P H， SHI P P. Application of modified SEIR epidemic dynamics model to prediction and evaluation of 2019 coronavirus disease （COVID-19） in Hubei Province ［J］. Journal of Zhejiang University （Medical Edition）， 2020， 49 （2）： 178-184.

［10］ CHEN D X， YANG Y F， ZHANG Y F， et al. Prediction of COVID-19 spread by sliding m SEIR observer［J］.Science China（Information Sciences），2020，63（12）：166-178.

［11］ EFIMOV D， USHIROBIRA R. On an interval prediction of COVID-19 development based on a SEIR epidemic model［J］. Annual Reviews in Control， 2021.

［12］ 林俊鋒. 基于引入隐形传播者的SEIR模型的COVID-19疫情分析和预测［J］. 电子科技大学学报，2020，49（3）：375-382.

LIN J F. Covid-19 epidemic analysis and prediction based on SEIR model with invisible communicators ［J］. Journal of University of Electronic Science and Technology， 2020，49 （3）： 375-382.

［13］ 邓春燕， 郭强， 傅家旗. 考虑人群流动数据的COVID-19传播模型［J］. 上海理工大学学报，2021，43（1）：59-67，92.

DENG C Y， GUO Q， FU J Q. Covid-19 propagation model considering crowd flow data ［J］. Journal of Shanghai University of Technology， 2021，43 （1）： 59-67 ， 92.

［14］ 廖影，张学良，焦海燕，等. 乌鲁木齐市COVID-19传播的动力学模型研究［J］. 中华疾病控制杂志，2021，25（8）：905-911，922.

LIAO Y， ZHANG X L， JIAO H Y， et al. Study on the dynamic model of covid-19 transmission in Urumqi ［J］. Chinese Journal of Disease Control， 2021，25 （8）： 905-911， 922.

［15］ 荆磊，刘明皓，陈春，等. 基于SEIRD-GEOCA的COVID-19疫情时空分布模型构建与情景模拟［J］. 西南大学学报（自然科学版），2022，44（2）：207-218.

JING L， LIU M H， CHEN C， et al. Construction and scenario simulation of COVID-19 epidemicspatio-temporal distribution model based on SEIRD-GEOCA ［J］. Journal of Southwest University （Natural Science Edition）， 2022，44 （2）： 207-218.

［16］ HE S， PENG Y， SUN K. SEIR modeling of the COVID-19 and its dynamics［J］. Nonlinear Dynamics， 2020， 101（3）： 1667-1680.

［17］ ANNAS S， PRATAMA M I， RIFANDI M， et al. Stability analysis and numerical simulation of SEIR model for pandemic COVID-19 spread in Indonesia［J］. Chaos， Solitons & Fractals， 2020， 139： 110072.

［18］ LIU C， HUANG J， JI F， et al. Improvement of the global prediction system of the COVID-19 pandemic based on the ensemble empirical mode decomposition （EEMD） and autoregressive moving average （ARMA） model in a hybrid approach［J］. Atmospheric and Oceanic Science Letters， 2021， 14（4）： 100019.

［19］ IHME COVID-19 forecasting team. Modeling COVID-19 scenarios for the United States［J/OL］. Nature Medicine. （2020-10-23）［2021-12-20］.DOI：10.1038/s41591-020-1132-9.

［20］ 邱明悦，胡涛，崔恒建. 双區间删失下新冠病毒肺炎潜伏期分布的参数估计［J］. 应用数学学报，2020，43（2）：200-210.

QIU M Y， HU T， CUI H J. Estimation of latent period distribution of COVID-19 pneumonia in double interval censored ［J］. Proceedings of Applied Mathematics， 2020，43 （2）： 200-210.

［21］ WANG D W， HU B， HU C， et al. Clinical characteristics of 138 hospitalized patients With 2019 novel coronavirus-infected pneumonia in Wuhan， China［J］. JAMA，2020，323（11）：1061-1069.

［22］ 韦爱举，张新建，王俊义，等. 一类埃博拉传染病模型的动力学分析［J］. 数学物理学报： A 辑， 2017， 37（3）： 577-592.

WEI A J， ZHANG X J， WANG J Y， et al. Dynamic analysis of a class of Ebola epidemic model ［J］. Journal of Mathematical Physics： Part A， 2017， 37 （3）： 577-592.

［23］ WALLINGA J， LIPSITCH M. How generation intervals shape the relationship between growth rates and reproductive numbers［J］. Proceedings of the Royal Society B： Biological Sciences， 2007， 274（1609）： 599-604.

（责任编辑 李 进）