BDS-2/BDS-3非组合观测模型的中距离相对定位

祝会忠，李 壮，雷啸挺

BDS-2/BDS-3非组合观测模型的中距离相对定位

祝会忠1,2，李 壮1，雷啸挺1

（1. 辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000；2. 卫星导航系统与装备技术国家重点实验室，石家庄 050081）

为了弥补北斗三号全球卫星导航系统（BDS-3）全星座、多频率相对定位以及组合定位方式相关研究的不足，提出一种BDS-2/BDS-3非组合观测模型的中距离相对定位方法：对BDS-3四频和北斗卫星导航（区域）系统（BDS-2）/BDS-3组合双频观测数据，采用多频载波相位观测数据非组合模型进行相对定位解算；分析BDS-2/BDS-3组合的定位性能，并与BDS-2三频、全球定位系统（GPS）双频解算结果进行对比；然后选取4条不同长度基线进行不同系统相对定位解算，对54 km基线充分考虑大气延迟误差的影响，并对定位性能进行分析。实验结果表明，BDS-3收敛速度相较于BDS-2有一倍的提升，并略优于GPS，定位精度相较BDS-2可提升大约40%，但略低于GPS；BDS-2/BDS-3组合模式收敛速度最快、定位精度最高，相较GPS在天顶（U）方向可有8.3%的提升，与BDS-3相比在U方向可有22.1%的提升；BDS-2/BDS-3双频组合定位性能优于GPS、BDS-2和BDS-3多频定位结果。

北斗卫星导航系统（BDS）；大气延迟误差；整周模糊度；收敛速度

0 引言

北斗卫星导航系统（BeiDou navigation satellite system，BDS）是中国自行研发的、继美国全球定位系统（global positioning system，GPS）和俄罗斯格洛纳斯卫星导航系统（global navigation satellite system， GLONASS）之后第3个成熟的全球卫星导航系统（global navigation satellite system，GNSS）。BDS建设按照“三步走”计划[1-2]，逐步向全球用户提供相关服务。北斗卫星导航（区域）系统即北斗二号（BeiDou navigation satellite (regional) system，BDS-2）包括5颗静止轨道卫星（geostationary Earth orbit，GEO）、7颗倾斜轨道卫星（inclined geosynchronous orbit，IGSO）以及3颗中圆轨道卫星（medium Earth orbits，MEO），满足为亚太地区服务的要求。北斗三号全球卫星导航系统（BeiDou-3 navigation satellite system，BDS-3）于2020年6月完成全球组网，BDS-3包括3颗GEO、3颗IGSO以及24颗MEO卫星，实现全球覆盖，可为全球用户提供卫星导航、定位、测速、授时、短报文通信、星际增强、国际搜救以及精密单点定位等服务。

BDS-2、BDS-3兼有有源、无源定位模式，服务范围更广，服务用户更多。BDS-2全星座播发三频信号，BDS-3除试验卫星和3颗GEO卫星，其他卫星均播发5个公开服务信号，BDS-3在BDS-2的基础上舍弃了B2I频率，增加了B2a、B2b和B1C 3个频率[3-4]，如表1所示。

表1 不同卫星系统频率

BDS-3从2015年3月开始发射试验卫星以来，国内外学者针对BDS-3在各方面的服务性能进行实验分析。文献[5]使用全球连续监测评估系统（international GNSS monitoring&assessment system，iGMAS）11个跟踪站数据，进行BDS-3试验卫星观测数据质量分析，得到BDS-3多路径效应、随机噪声、轨道误差均小于BDS-2，新型原子钟性能也优于BDS-2的结果。文献[6]在考虑载噪比、多路径、噪声的基础上评估BDS-3的定位性能，可知，在各频点上BDS-2与BDS-3噪声大小相当，后者有更高的数据质量，在BDS-2加入BDS-3后，改善了卫星几何图形结构，提高了定位精度。文献[7]对BDS-3提供的5个频率的观测数据分别进行三频、四频、五频的模糊度解算。在不同基线长度条件下，频率越多得到的数据质量越好，模糊度固定变得更加高效可靠。文献[8]-[9]顾及系统间偏差，在多系统重叠频率间、接收机相同的条件下，对BDS-3分析伪距和载波的定位精度，得到BDS-3相同频段上伪距观测噪声与BDS-2相同，相位观测噪声略低于BDS-2的结果。可忽略系统间偏差进行组合，在卫星可见数少的复杂环境下能够明显提高模糊度固定成功率，多系统组合定位时，BDS-2/BDS-3组合的定位结果有更高的固定率，但浮点解精度不如BDS-3/GPS组合定位的结果。文献[10]评估了不同系统实验星重叠频率差分系统间偏差（differential inter-system bias，DISB）的大小和稳定性，在组合相对定位中可忽略其影响。在单系统卫星数较少，仅单频观测值可用情况下，紧组合模型相较于传统的松组合模型，模糊度固定成功率可提升约25%～45%。文献[11]针对组合定位方式的定位性能问题，采用双差模型进行短基线解算，结果表明，针对小范围内（距离小于5 km）的短基线，BDS-2/BDS-3的组合定位方式相较于单BDS-2和GPS在定位精度上都有很大提升，且定位精度都在5 mm以内。文献[12]使用多模GNSS试验跟踪网（multi-GNSS experiment, MGEX）和iGMAS跟踪网观测数据计算BDS-3试验卫星精密轨道，实验通过比较接收机钟差和B1I、B3I频间偏差，证实在BDS-2、BDS-3试验卫星2种相同频率B1I、B3I上不存在明显的系统间偏差。文献[13]基于卫星分布概率，对BDS在全球范围的可见卫星数和精度因子进行了预测和评估，分析了BDS-2和BDS-3在中国和全球区域的定位精度差异，得到在中国区域内，BDS-3的可见卫星数为7～15颗，相较于BDS-2，其GEO/IGSO卫星覆盖下降，但MEO可见卫星数增加，在中国区域精度相比全球范围提升4%～13%的结论。

针对BDS-3全星座、多频率相对定位以及组合定位方式的研究较少，而且相关研究不够深入的问题，为验证BDS-3的定位性能，本文全面考虑涉及大气误差改正、模糊度固定等过程相关因素，自编GNSS相对定位软件，使用BDS-3多频率观测数据进行不同长度基线解算，评估 BDS-3多星座、多频率相对定位的稳定性、收敛速度、定位精度等。同时，基于当前在变形监测、灾害监测时所需的定位精度高的现状，对BDS-2/BDS-3双频组合进行性能评估。BDS-2和BDS-3信号B1I和B3I频率相同，可以在BDS双频条件下进行组合，并且在亚太地区可见卫星数量多，可以提供更高精度的定位，满足灾害监测需求的同时节省成本。

1 数学模型

短距离相对定位时由于误差相关性高，双差可以近似消去，而较长距离相对定位的误差受到残余电离层延迟与对流层延迟的影响较大，必须考虑其对整周模糊度固定和定位精度的影响，算法以长距离相对定位算法为例（短距离时可认为大气误差项均为零）。由于BDS-2和BDS-3的B1I和B3I频率相同，进行组合兼容性好，在接收机型号相同时无须考虑系统间偏差，因此观测方程与单系统相同。BDS伪距和载波相位长基线单差基础观测方程为：

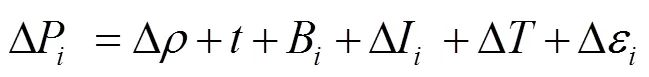
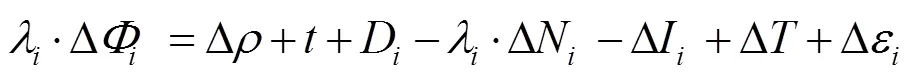
短基线求差后大气延迟影响可以消除或者可以忽略不计，不会影响模糊度的固定。面对基线较长的载波相位整周模糊度和位置参数解算时，大气延迟相关性降低，相对定位时无法将大气误差降低到半个波长以下。考虑到大气延迟误差的影响，想要成功固定整周模糊度就需要在观测方程中增加电离层、对流层作为未知参数，以分离出未完全消除的大气延迟误差，减小残余误差对模糊度固定的影响，进而成功固定载波相位整周模糊度。

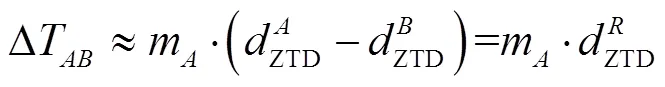
站间差分载波相位观测方程以整周模糊度作为参数进行估计，为便于模糊度解算过程中基准卫星变换，利于对大气延迟误差进行约束，测站间单差方程中未知参数以单颗卫星为对象，选取初始高度角较高的卫星伪距观测值粗略计算出基准模糊度数值作为初始值。伪距观测方程与载波相位观测方程中对流层延迟参数相同，电离层延迟参数大小相等、符号相反，组合观测方程可加强对电离层延迟误差残余和对流层延迟误差参数的约束[17]。载波相位观测值相观测精度远高于伪距并且伪距观测值噪声很大，根据经验值对2个观测方程按照1︰10000的权重置权，进行法方程叠加后对未知参数进行估计。由于观测方程中未知参数过多，使方程性质减弱难以解算，为避免法方程的奇异性和增强定位解的强度，根据大气误差随时间变化呈现随机游走的特性，给对流层和电离层以先验约束作为附加观测值，进行大气误差的随机游走约束。天顶对流层延迟误差和电离层延迟误差历元间随机游走约束[18-20]方程为：

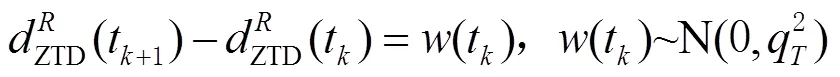
使用上述观测方程进行解算，首先求得位置参数初始值以及模糊度浮点解，使用模糊度浮点解以及对应的方差协方差矩阵进行最小二乘模糊度降相关平差法（least square ambiguity decorrelation adjustment，LAMBDA）的模糊度搜索，得到模糊度整数解，并根据比率（ratio）值进行模糊度解算判断[21]，如果ratio值大于3则认为模糊度解算正确，并将整周模糊度重新带入方程，进行测站坐标解算。

2 实验与结果分析

为了评价BDS-2、BDS-3、GPS、BDS-2/BDS-3四种解算模式的相对定位精度，本文选择了4条不同长度的基线进行实验，并对实验结果进行收敛时间、收敛精度的统计分析。

数据采集采样间隔设置为1 s，使用上述数学模型中相关算法进行BDS-2三频、BDS-3四频、GPS双频、BDS-2/BDS-3组合系统双频数据解算。GPS部分卫星有三频信号，但是卫星数量少，因此选用GPS双频进行解算。数据解算时截止高度角设置为15°，采样间隔为1 s，由于不同长度基线模糊度固定所需时间不同，基线越长收敛时间越长，为了充分体现不同长度基线定位效果，对不同长度基线进行不同时段长度的解算，其中对1、20、37 km基线每10 min为一个时段，对54 km基线每1 h为一个时段进行相对定位数据解算，采集观测数据信息如表2所示。

表2 基线信息统计

大气延迟误差随着基线的长度增加而不断增大，而且定位时无法对大气延迟误差进行预测和实时解算；不进行大气改正，长基线相对定位整周模糊度难以固定。研究发现大气延迟有随机游走特性，在进行长基线解算时采用的随机游走约束，实质就是认为电离层延迟、对流层延迟在前后2个较短时间间隔内大气变化很小，近似相等，而进行历元间消除。对流层和电离层延迟变化相对稳定的时段给与紧约束，变化不稳定的时段则施加宽松随机游走约束，更利于数据的解算和未知参数求解。BDS-3的54 km基线C35、C39、C40、C44四颗卫星电离层延迟如图1所示。

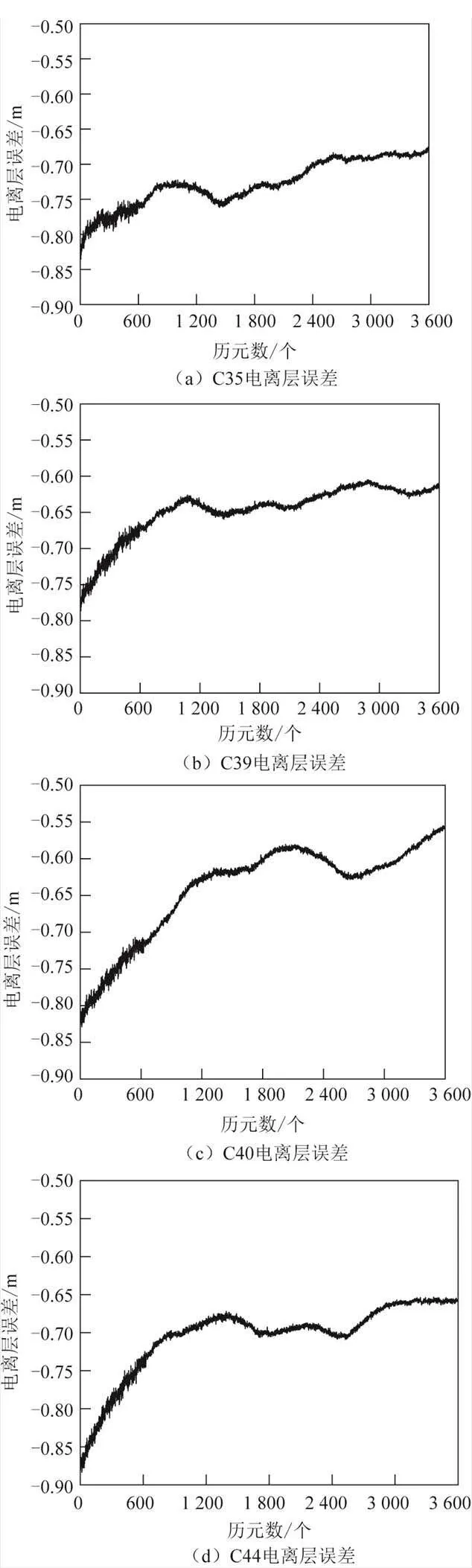
图1 54 km基线C35、C39、C40及C44卫星的电离层误差

从图1可以看出，电离层延迟误差变化量已经大于个载波相位半波长的长度，并且还有多路径效应、观测噪声等影响，会导致整周模糊度难以固定。所以在观测方程中增加大气延迟参数，对残余大气延迟误差进行估计分离，以实现整周模糊度的准确固定。54 km基线整周模糊度浮点解收敛过程如图2所示。

模糊度固定过程中，对大气延迟误差及其他误差进行约束消除，当误差对模糊度固定干扰小于载波相位的半个波长时，整周模糊度就很容易固定。从54 km基线模糊度浮点解可看出整周模糊度收敛较快，模糊度浮点解很快稳定在准确的整周模糊度附近；使用LAMBDA算法搜索固定解时，计算量小且解算成功率更高。

基线均处于中国境内，BDS 的GEO、IGSO卫星数量可见性高，能观测到的共视BDS卫星数目较多。从卫星数量图中看出在低纬度地区，BDS-2卫星最多观测到13颗、最少观测到8颗，卫星可见数明显高于BDS-3和GPS，随着纬度的上升，BDS-2共视卫星数目略有下降，这是因为BDS-2卫星主要覆盖区域在北纬30°—南纬30°、东经90°—150°范围内。BDS-3与GPS同为全球卫星导航系统，卫星主要以MEO为主，卫星总量与GPS数目相当，但是BDS-3卫星轨道不如GPS合理，所以共视卫星数量少于GPS或与GPS卫星数量相当，卫星数目一般在8颗左右。而对于BDS-2/BDS-3组合的定位方式，卫星可见数在15～22颗，对比可知具有远超过单系统的数量，这也是组合定位方式的优势之一。

短基线观测数据解算600个历元分为一个时段，1 km基线十分稳定，20与37 km基线相似（如图3～图8所示），因为基线较短，求差过程中接收机钟差、卫星钟差、硬件延迟偏差、大气延迟误差等相关性很强，也可以近似消去，所以BDS-2、BDS-3、GPS、BDS-2加BDS-3四种定位方式均能在第一个历元完成模糊度固定，得到收敛解，收敛速度相同。

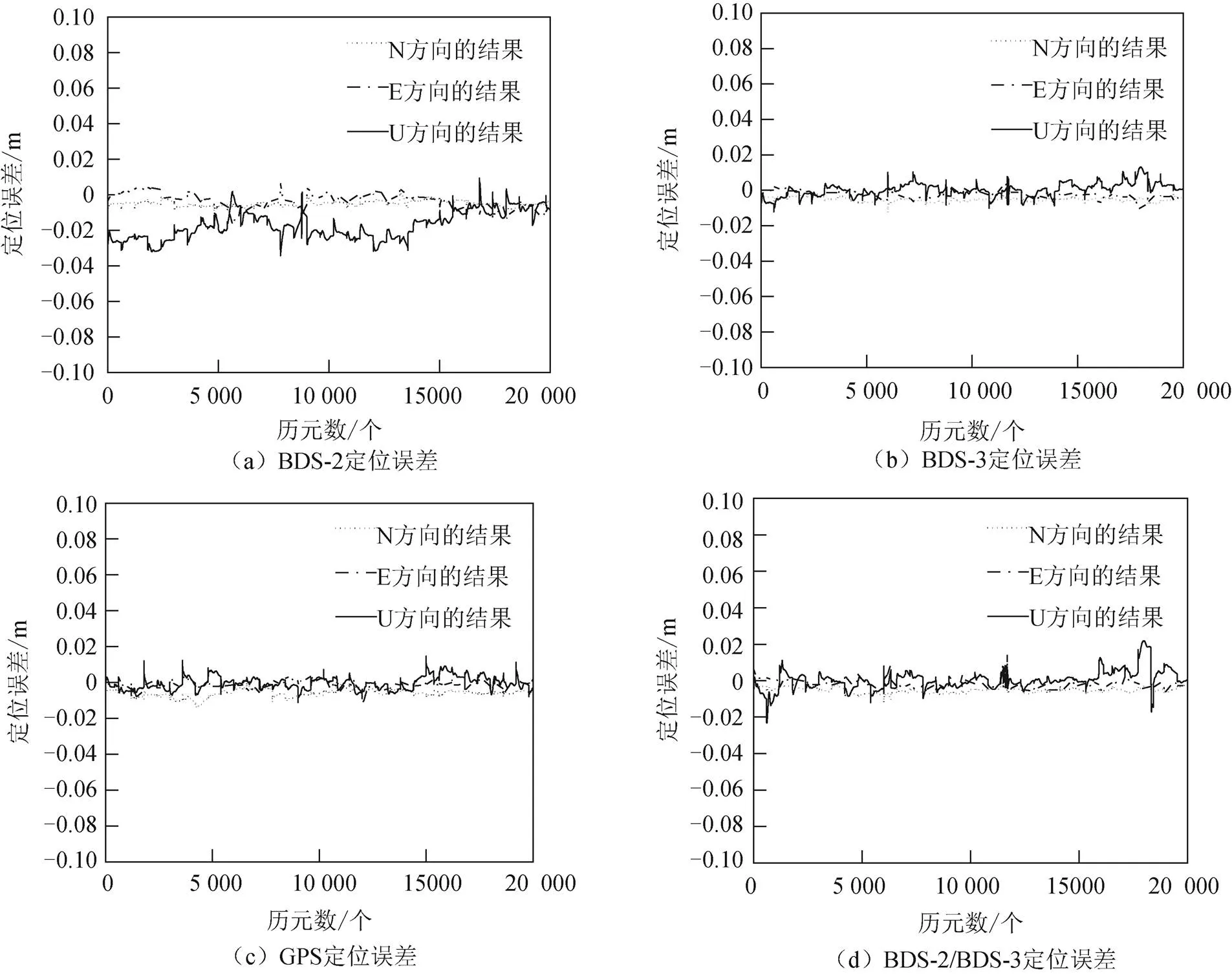
图3 1 km基线的定位误差

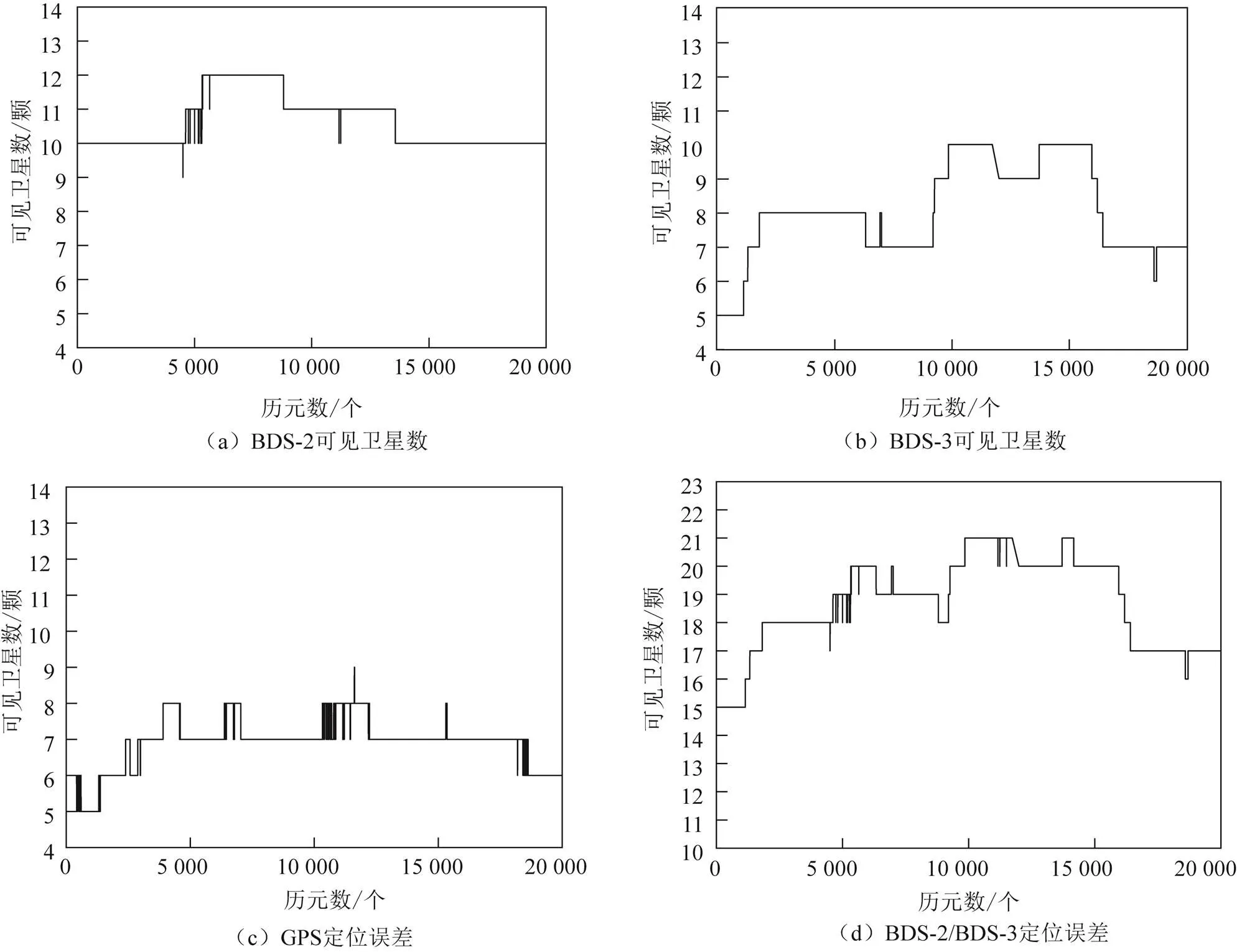
图4 1 km基线的可见卫星数

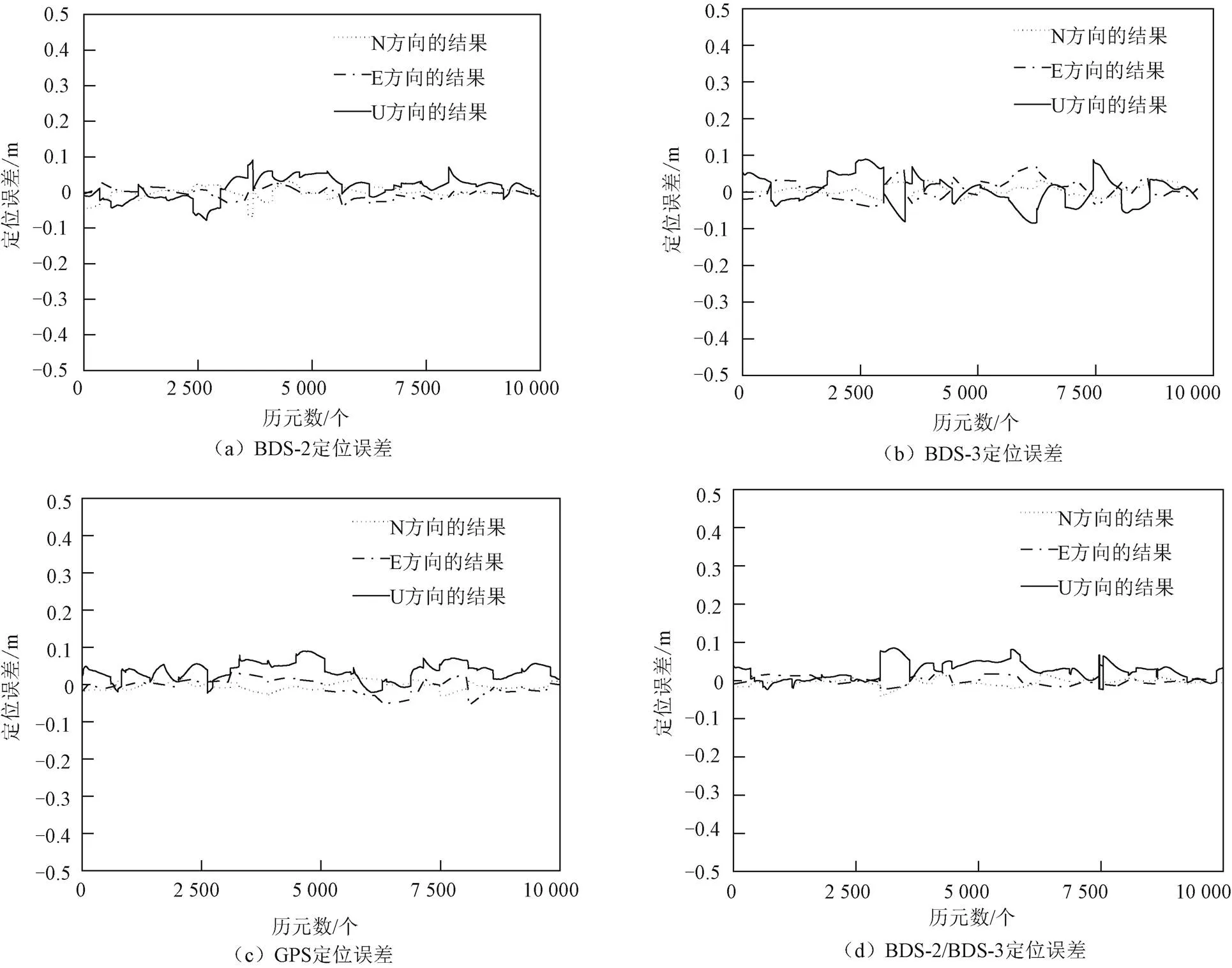
图5 20 km基线的定位误差

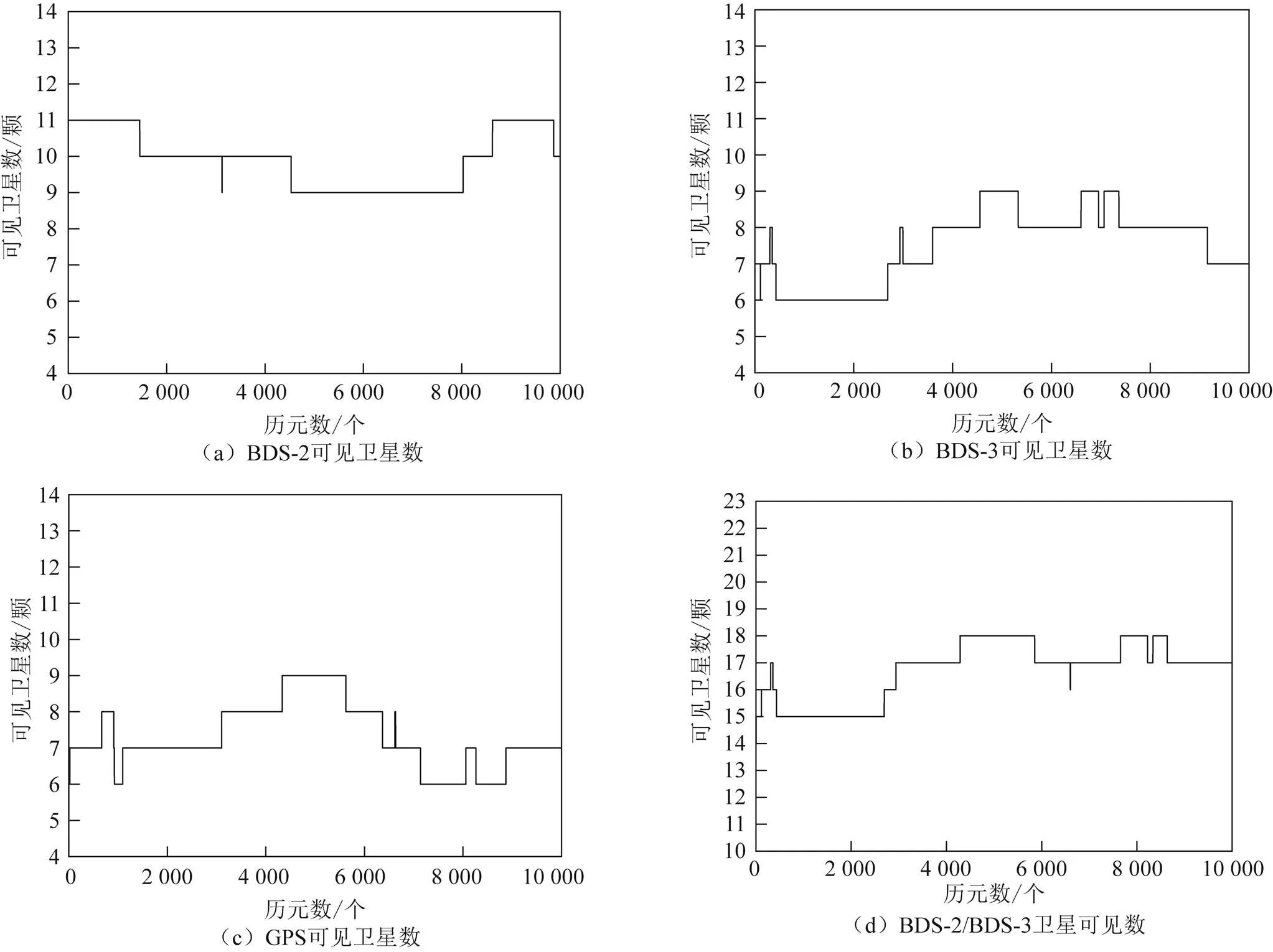
图6 20 km基线的可见卫星数

图7 37 km基线的定位误差

图8 37 km基线的可见卫星数

可以看出54 km基线的解算收敛速度与卫星数量有较强的相关性，卫星数量多且卫星变化较为稳定的时段收敛速度较快，当卫星数量较少或者卫星变化较大时结算收敛速度和精度都会下降（如图9、图10所示）。

收敛时间统计是按照定位精度达到厘米级则认为其收敛，因为1、20、37 km基线均可在单历元内收敛，所以未统计在收敛时间统计表内。对54 km基线每个时段的收敛时间统计结果如表3所示。

偏差统计是统计每个时段解算的最终偏差值，再求其平均值，4条基线分别对4种定位方式偏差进行统计。得到误差平均值统计结果如表4～表7所示，统计图如图11所示。

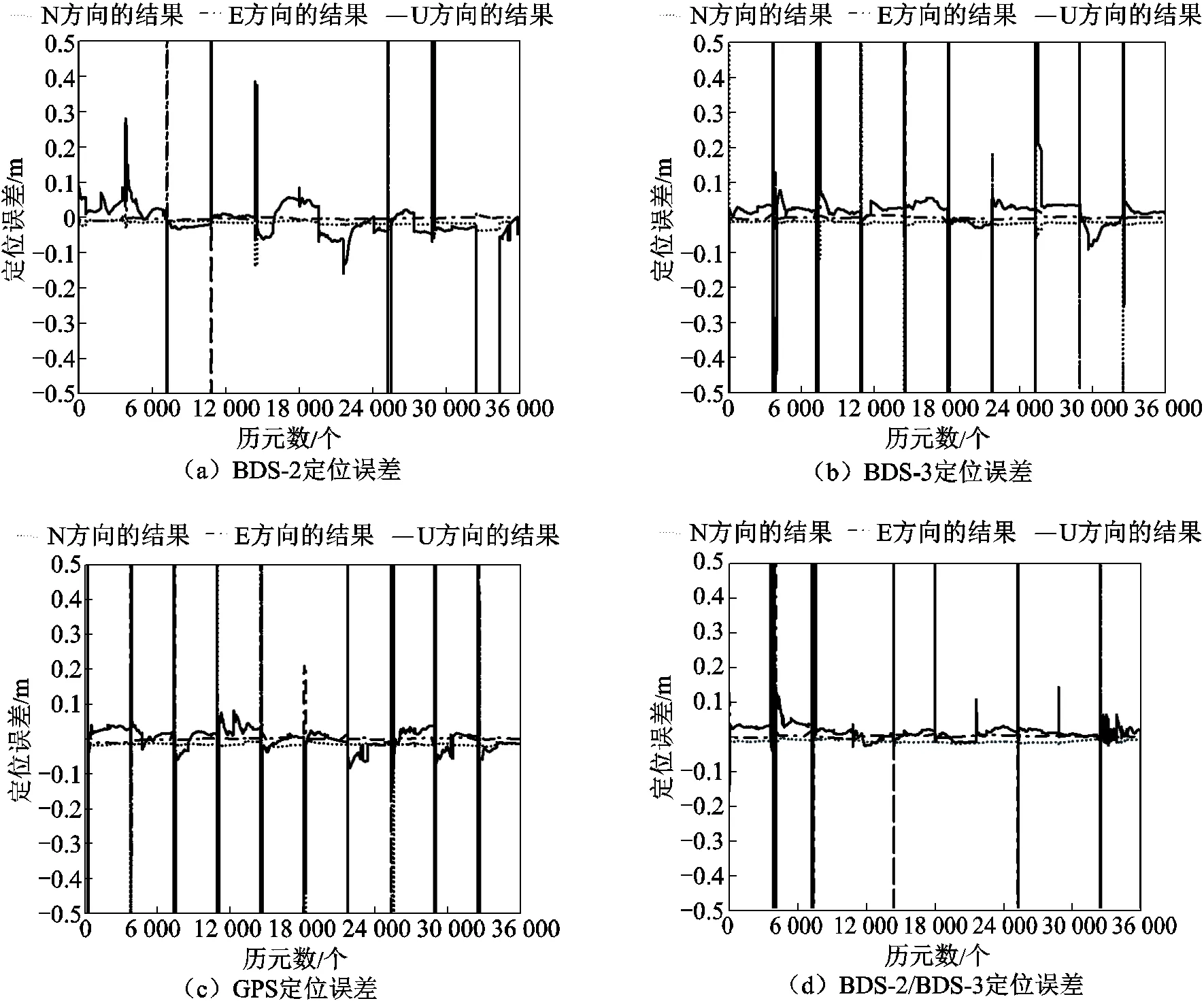
图9 54 km基线的定位误差

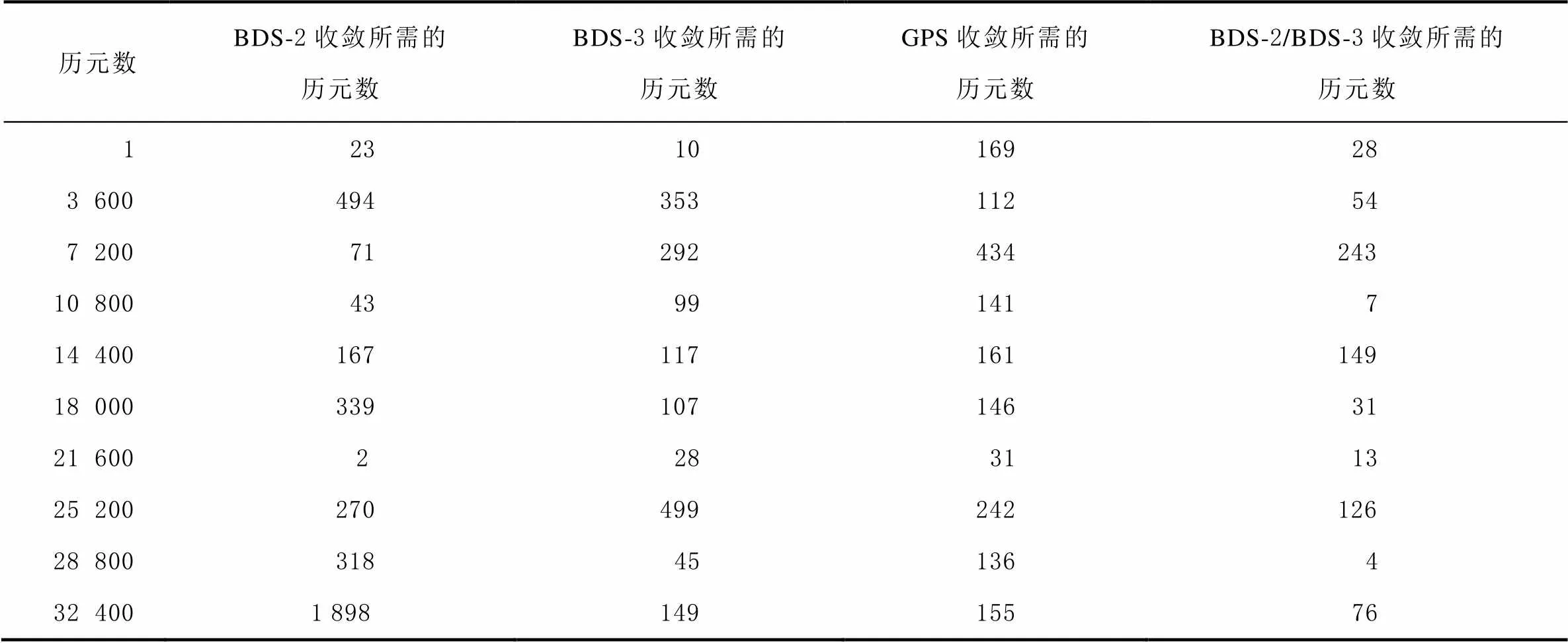
表3 收敛时间统计 个

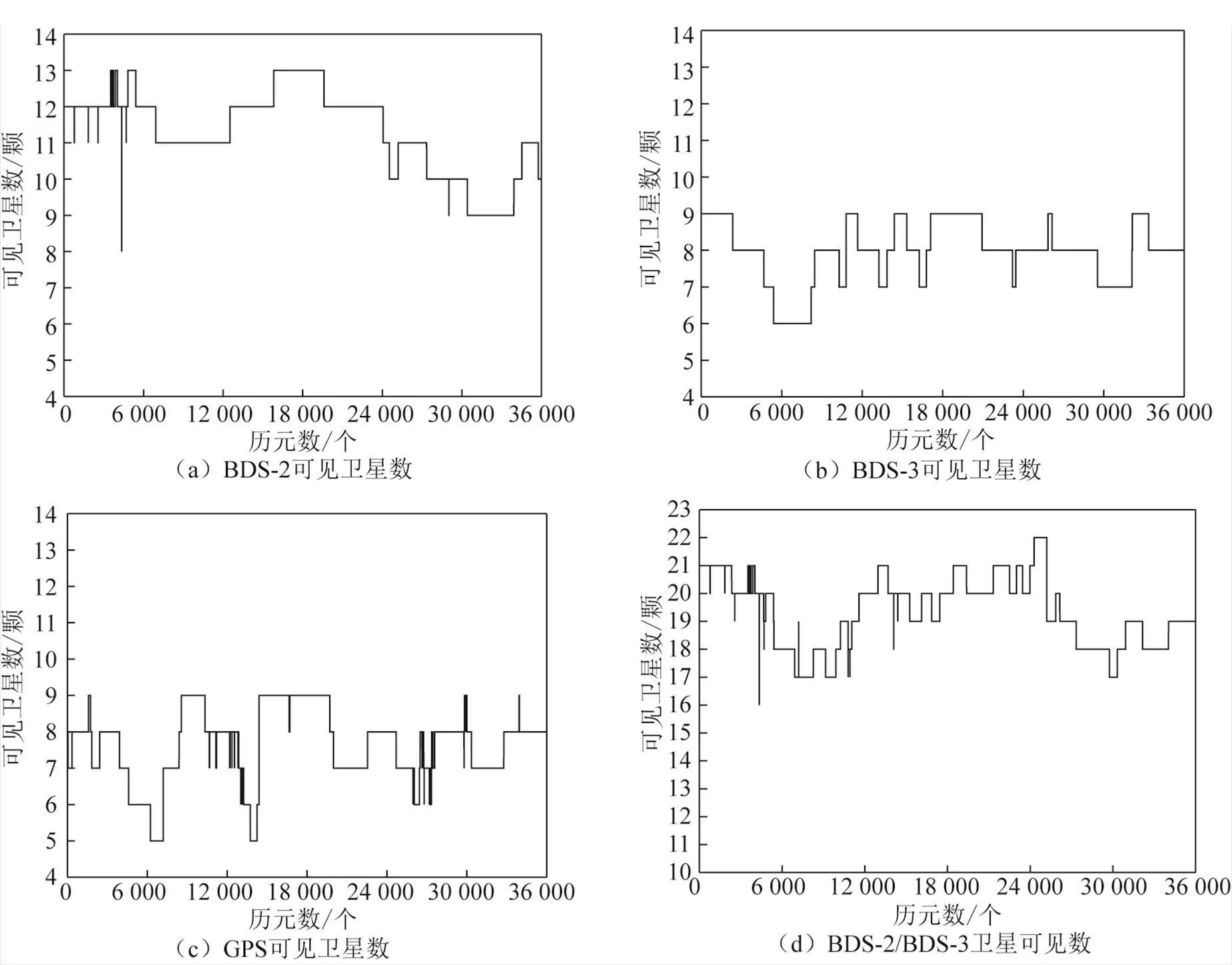
图10 54 km基线的可见卫星数

表4 1 km基线的定位偏差统计 m

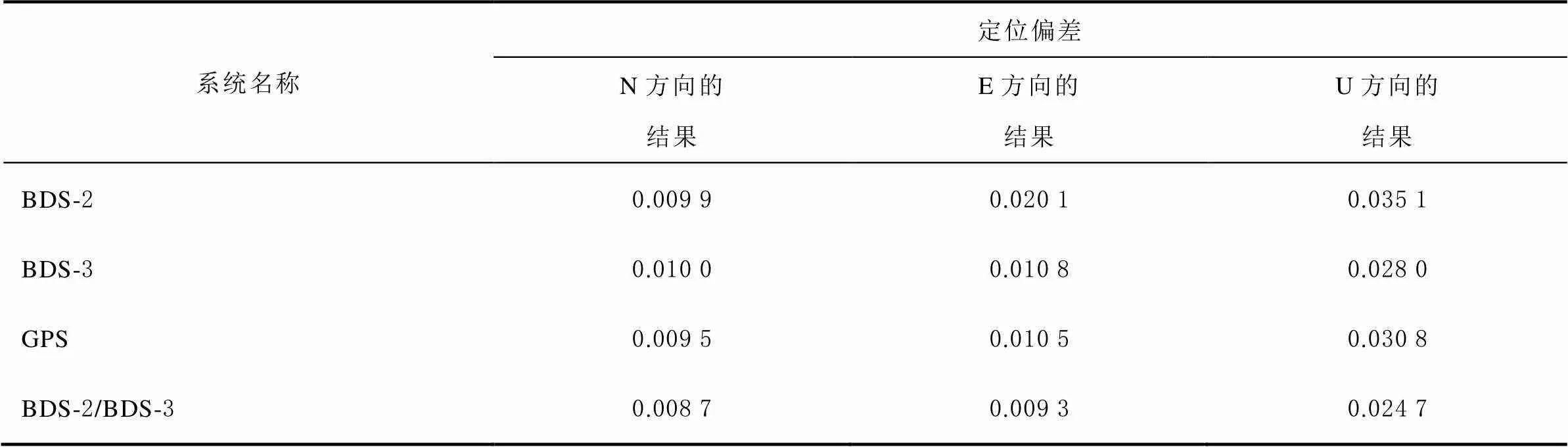
表5 20 km基线的定位偏差统计 m

表6 37 km基线的定位偏差统计 m

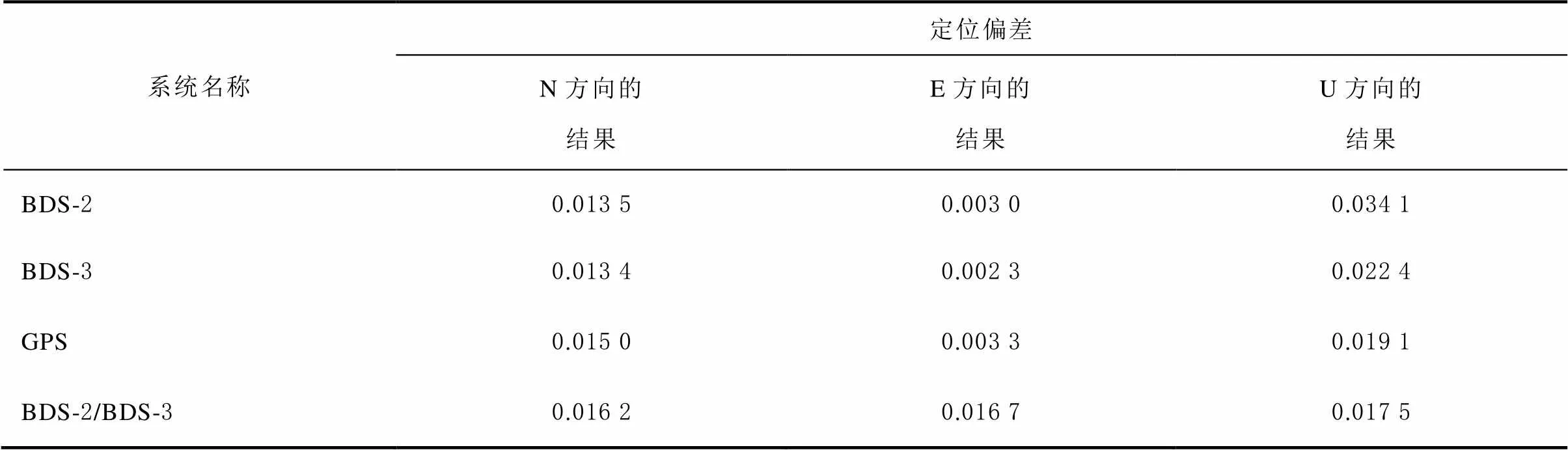
表7 54 km基线的定位偏差统计 m

图11 4条基线N、E、U方向定位偏差统计

从统计结果看出：1、20、37 km基线这3条基线，4种定位方式均为单历元收敛固定模糊度。1 km基线的定位偏差平均值相近；20 km基线、BDS-2精度较其他系统较差，精度控制在4 cm以内；37 km基线的解算，虽然BDS-2与另外3种定位方式收敛速度相同，均能单历元固定模糊度，但是因为残余误差影响，定位精度低于前2条基线定位精度；54 km基线，无论是收敛速度还是定位精度，BDS-2都是最差的。虽然BDS-2可见卫星数目多于BDS-3和GPS，但是定位性能很差，主要原因是：BDS-2观测到的卫星多为GEO和IGSO卫星，2种卫星轨道高度均为36000 km，运行周期较长，接收机观测时，卫星运行速度缓慢，构成的星座几何构型差，不利于观测数据的连续解算，所以收敛时间较长；而且BDS-2因为卫星原子钟、卫星轨道精度、卫星硬件延迟、信号抗干扰能力弱等因素影响，精度也低于更完善的BDS-3和GPS。BDS-2/BDS-3的组合方式弥补了这一缺陷，相比于BDS-3增加了可见卫星数。BDS-2收敛时间会随着MEO卫星数量的增加而缩短，因为MEO卫星轨道低、运行速度快，连续解算时卫星星座几何构型变化加速，所以当观测的卫星MEO数量多时，对BDS-2定位收敛速度有提升效果。

由精度统计结果看出，随着基线长度的增加，模糊度固定的时间也不断增加，定位精度有所降低。因为即使对大气延迟进行了约束，仍不能完全消除大气延迟误差的影响，残余的大气误差会使模糊度固定速率减慢，在模糊度准确固定情况下大气延迟误差被坐标参数吸收，导致定位精度不高。坐标精度U方向偏差最大，一般经验U方向误差为N、E方向误差的1.5倍，主要是因为卫星轨道残余误差和对流层延迟误差对U方向影响较大。

BDS-3和GPS主要是MEO卫星，卫星几何构型较好，适合于数据连续解算。BDS-3播发4个频率信号，冗余观测较多，信号抗干扰能力更强，卫星数目多、几何构型好，所组的法方程利于参数解算。在卫星星历及相关改正模型不及GPS的情况下，解算速度和定位精度略差于GPS。从定位偏差图可以看出，BDS-2/BDS-3的精度最优，BDS-3定位精度远胜于BDS-2，与GPS接近；但是BDS-3定位过程中易受到其他误差干扰，系统稳定性不如GPS。

3 结束语

本文对采集的数据分别进行BDS-2三频、BDS-3四频、GPS双频以及BDS-2/BDS-3组合4种相对定位，选择长度为1、20、37以及54 km的4条基线分别进行解算。短基线条件下因为站间误差相关性强，可以近似消去；随着测站距离的扩大，大气延迟难以消除。通过对大气延迟等误差进行分析，设置大气延迟误差参数，为增加方程强度添加随机游走约束，实现了模糊度准确固定，完成了高精度定位。对实验结果进行分析得到以下结论：

1）BDS-3整体定位精度相较于BDS-2提升了大约40%，但精度略低于GPS。

2）BDS-3收敛速度相较于BDS-2有一倍的提升，并略优于GPS。

3）BDS-3已经完成全球组网，相较于BDS-2在各个方面都有很大改善，但是BDS-3整体定位性能不如GPS。

4）BDS-2/BDS-3组合模式下收敛速度最快、定位精度最高，其平面精度可达2 cm，高程精度可达3 cm，其中与GPS相比在U方向上有8.3%的提升，与BDS-3相比在U方向上有22.1%的提升。

[1] 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J].测绘学报, 2010, 39(1):1-6.

[2] 杨元喜, 李金龙, 徐君毅, 等.中国北斗卫星导航系统对全球PNT用户的贡献[J]. 科学通报, 2011, 56(21): 1-7.

[3] 中国卫星导航系统管理办公室. 北斗卫星导航系统公开服务性能规范(2.0版)[EB/OL]. (2020-11-19)[2022-04-27]. http://www.beidou.gov.cn.

[4] 中国卫星导航系统管理办公室. 北斗卫星导航系统空间信号接口控制文件公开服务信号B1I (3.0版)[EB/OL]. (2019-04-08)[2022-04-27]. http://www.beidou.gov.cn.

[5] XIE Xin, GENG Tao, ZHAO Qile, et al. Performance of BDS-3: measurement quality analysis,precise orbit and clock determination[J]. Sensors, 2017, 17(6): 1-14.

[6] 程军龙, 王旺, 马立烨, 等. 北斗三号观测数据质量及定位精度初步评估[J]. 测绘通报, 2019(8): 1-7.

[7] 章浙涛, 李博峰, 何秀凤. 北斗三号多频相位模糊度无几何单历元固定方法[J]. 测绘学报, 2020, 49(9): 1139-1148.

[8] 朱松, 李玮. BDS-3卫星信号质量及RTK定位分析[J]. 测绘科学, 2022, 47(1): 1-8. DOI:10.16251/j.cnki.1009-2307.2022.01.001.

[9] 曹相, 王庆, 高成发, 等. 基于BDS-3、GPS和Galileo重叠频率观测值的紧组合RTK定位方法[J]. 仪器仪表学报, 2019, 40(10): 138-144. DOI:10.19650/j.cnki.cjsi.J1905473.

[10] 吴明魁, 刘万科, 张小红, 等. GPS/Galileo/BDS-3试验星短基线紧组合相对定位性能初步评估[J]. 武汉大学学报(信息科学版), 2020, 45(1): 13-20. DOI:10.13203/j.whugis20180269.

[11] 金俭俭, 高成发, 张瑞成, 等. GPS与BDS-2、BDS-3融合数据短基线解算精度分析[J]. 测绘通报, 2020(3): 83-86, 95. DOI:10.13474/j.cnki.11-2246.2020.0083.

[12] LI Xingxing, YUAN Yongqiang, ZHU Yiting, et al. Precise orbit determination for BDS-3 experimental satellites using iGMAS and MGEX tracking networks[J]. Journal of Geodesy, 2019, 93(1): 103-117.

[13] 崔浩猛, 王解先, 王明华, 等. 利用卫星分布概率对BDS-3性能的评估[J]. 武汉大学学报(信息科学版), 2021, 46(6): 938-946. DOI:10.13203/j.whugis20190172.

[14] FAN Haopeng, SUN Zhongmiao, ZHANG Liping, et al. A two-step estimation method of troposphere delay with consideration of mapping function errors[J]. Journal of Geodesy and Geoinformation Science, 2020, 3(1):76-84．

[15] 毛健, 崔铁军, 李晓丽, 等. 融合大气数值模式的高精度对流层天顶延迟计算方法[J]. 测绘学报, 2019, 48(7): 862-870.

[16] YAO Yibin, ZHAO Qingzhi. A method to improve the utilization of GNSS observation for water vapor tomography[J]. Annales Geophysicae, 2016, 34(1): 143-152.

[17] 祝会忠, 雷啸挺, 徐爱功, 等. 顾及GEO卫星约束的长距离BDS三频整周模糊度解算[J]. 测绘学报, 2020, 49(9): 1222-1234.

[18] TANG Weiming, LIU Wenjian, ZOU Xuan, et al. Improved ambiguity resolution for URTK with dynamic atmosphere constraints[J]. Journal of Geodesy, 2016, 90(12): 1359-1369．

[19] ZHANG Xiaohong, REN Xiaodong, WU Fengbo, et al. Short-term prediction of ionospheric TEC based on ARIMA model[J]. Journal of Geodesy and Geoinformation Science, 2019, 2(1): 9-16.

[20] 陈正生, 张清华, 李林阳, 等. 电离层延迟变化自模型化的载波相位平滑伪距算法[J]. 测绘学报, 2019, 48(9): 1107-1118.

[21] 祝会忠, 雷啸挺, 李军, 等. BDS参考站三频整周模糊度单历元确定方法[J]. 测绘学报, 2020, 49(11): 1388-1398.

Relative positioning at medium distance for BDS-2/BDS-3 un-combined observation models

ZHU Huizhong1,2, LI Zhuang1, LEI Xiaoting1

（1. School of Geomatics, Liaoning Technical University, Fuxin, Liaoning 123000, China;2. The State Key Laboratory of Satellite Navigation System and Equipment Technology, Shijiazhuang 050081, China）

In order to make up for the deficiency of the related study on the whole constellation, multi-frequency relative positioning and combined positioning of the BeiDou-3 navigation satellite system (BDS-3), the paper proposed a relative positioning method at medium distance for BeiDou navigation satellite (regional) system (BDS-2)/BDS-3 un-combined observation models: for BDS-3 four-frequency and BDS-2/BDS-3 dual-frequency observations, the uncombined model of multi-frequency carrier phase observations was used for relative positioning solution; and the positioning performance of the BDS-2/BDS-3 was analyzed and compared with the BDS-2 three-frequency and global positioning system (GPS) dual-frequency positioning results; then four different length baselines were selected for the relative positioning solutions for different systems, and the influence of atmospheric delay error was fully considered for the 54 km baselines to further improve the positioning performance. Experimental results showed that the convergence rate of BDS-3 would be twice higher than that of BDS-2, and slightly better than that of GPS, and the positioning accuracy could be improved by about 40% compared with BDS-2, but slightly lower than that of GPS; the combined mode of BDS-2/BDS-3 would have the fastest convergence speed and the highest positioning accuracy, with an 8.3% improvement in the U-direction compared with GPS, and a 22.1% improvement in the U-direction compared with BDS-3; the BDS-2/BDS-3 dual-frequency combined positioning performance could be better than the multi-frequency positioning results of GPS, BDS-2 and BDS-3.

BeiDou navigation satellite system (BDS); atmospheric delay constraint; integer ambiguity; convergence speed

P228

A

2095-4999(2023)02-0049-12

祝会忠, 李壮, 雷啸挺. BDS-2/BDS-3非组合观测模型的中距离相对定位[J]. 导航定位学报, 2023, 11(2): 49-60.（ZHU Huizhong, LI Zhuang, LEI Xiaoting. Relative positioning at medium distance for BDS-2/BDS-3 un-combined observation models[J]. Journal of Navigation and Positioning, 2023, 11(2): 49-60.）DOI:10.16547/j.cnki.10-1096.20230206.

2022-06-13

国家自然科学基金项目（42030109，42074012）；卫星导航系统与装备技术国家重点实验室开放基金项目（CEPNT-2018KF-13）；辽宁省重点研发计划项目（2020JH2/10100044）；辽宁省“兴辽英才计划”项目（XLYC2002101，XLYC2008034，XLYC2002098）。

祝会忠（1983—），男，河南安阳人，博士，教授，研究方向为GNSS高精度数据处理及应用。