GNSS非组合精密单点定位模型算法与应用

张宝成，刘 腾，徐 黎,2，高 睿,2

GNSS非组合精密单点定位模型算法与应用

张宝成1,3，刘 腾1，徐 黎1,2，高 睿1,2

（1. 中国科学院 精密测量科学与技术创新研究院大地测量与地球动力学国家重点实验室，武汉 430077；2. 中国科学院大学，北京 100049；3. 中国电子科技集团公司第五十四研究所 卫星导航系统与装备技术国家重点实验室，石家庄 050002）

为了进一步发展全球卫星导航系统（GNSS）非组合精密单点定位技术（PPP），研究其算法和应用：构建非组合PPP从单频到多频、从单系统到多系统的满秩函数模型，并介绍各类非组合PPP模型的秩亏消除策略及待估参数形式；然后结合非组合PPP技术特色，论述其在对流延迟和电离层延迟提取、差分码偏差估计和精密授时方面的典型应用；最后针对最新发展动态，展望非组合PPP技术今后的发展趋势。

全球卫星导航系统（GNSS）；北斗导航卫星系统（BDS）；非组合精密单点定位（PPP）；码偏差短时变化

0 引言

全球卫星导航系统（global navigation satellite system, GNSS）包括美国的全球定位系统（global positioning system，GPS）、俄罗斯格洛纳斯卫星导航系统（global navigation satellite system, GLONASS）、欧盟的伽利略卫星导航系统（Galileo navigation satellite system，Galileo）和中国的北斗卫星导航系统（BeiDou navigation satellite system，BDS）及其他区域导航系统，是一种重要的大地测量手段，可为用户提供全天时、全天候的导航、定位与授时服务。

精密单点定位技术（precise point positioning，PPP）是GNSS中尤为重要的定位技术，不同于传统实时动态差分（real-time kinematic，RTK）技术依赖附近的参考站来获取精密位置，它利用高精度的卫星轨道和钟差产品，并严密考虑卫星端、信号传播路径和用户端相关的各类系统误差的影响，同时求解用户坐标、接收机钟差、对流层延迟、电离层延迟、相位模糊度等参数，可在全球范围内任意一点获得厘米级到分米级的绝对定位精度[1-2]。PPP技术有效避免了RTK技术中不同测站数据由于差分而导致的相关性问题，数据处理可采用逐测站处理的方式，时间复杂度随测站个数线性增长，效率较高，在实施中也无需基准站，更为灵活，已被广泛应用到精密定位、授时、大气延迟提取及其他相关地球科学研究中[3-7]。

PPP模型按照对电离层延迟处理方式的不同大致可分为消电离层组合模型和非组合模型。消电离层组合模型也可细分为2类：一是PPP技术在提出时采用的是双频伪距和相位观测值形成的消电离层组合观测值，是目前应用最广泛的模型[1-2]；二是加拿大卡尔加里大学高扬教授提出的卡尔加里大学（University of Calgary, UofC）模型，该模型利用伪距和相位观测值上电离层延迟大小相等、符号相反的特性，将各频点上的伪距和相位观测值相加，以达到消除电离层延迟的目的[8]。非组合模型是近年来新发展起来的一种PPP模型，该模型直接使用原始伪距和载波相位观测值，将电离层斜延迟参数化，并与其他参数一起解算[9-10]。非组合模型相对于消电离层组合模型具有以下优势：直接利用原始伪距和载波相位观测值，避免了传统模型形成消电离层组合时造成的观测噪声与未模型化误差放大与信息损失[11-12]；在处理GNSS多频数据时，避免了消电离层组合的最优化选择问题，且不同频率模型中均使用原始观测值，有利于模型的统一表达，在算法实现中更为灵活，更适合多模多频精密单点定位的实施[13-14]；在参数域保留了电离层延迟信息，可以通过引入外部的电离层信息约束来加快定位收敛速度，进一步提高定位性能[15]；也可独立提供高精度的电离层斜延迟信息，为电离层建模和频间偏差估计提供精确的电离层延迟信息[3-4,10,16]。基于非组合模型的众多优势，近年来诸多学者对非组合精密单点定位算法与应用进行了研究，并取得一系列研究成果。

1 非组合PPP模型与算法

伪距和载波相位观测值是GNSS最基本的观测量，其中伪距观测值是一种绝对距离观测量，精度一般在分米到米级；载波相位观测值是一种相对距离观测量，具有很高的精度，一般在毫米量级。线性化后的GNSS伪距和载波相位观测方程[17]可表达为

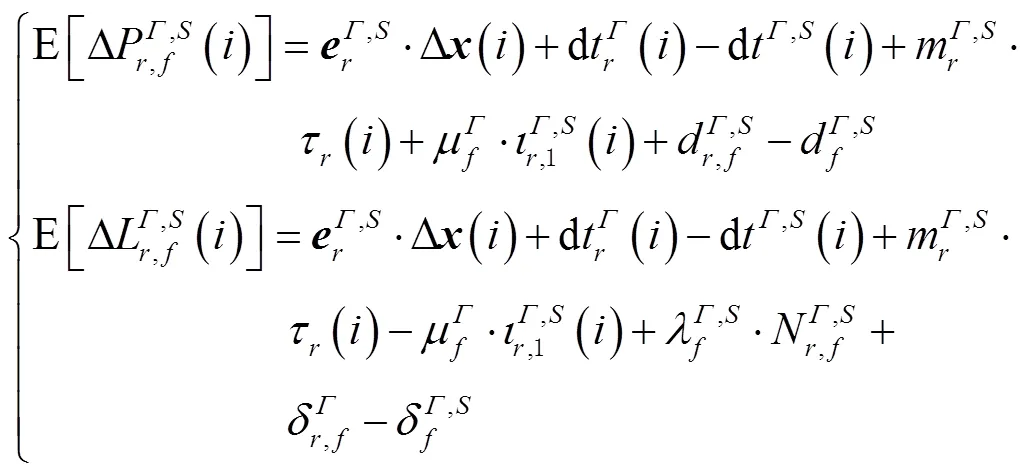
1 单频非组合PPP模型

1.1.1 单频非组合电离层浮点模型

观测方程式（1）采用第一频率的观测值，并用国际GNSS服务组织（international GNSS service，IGS）精密卫星钟差产品改正后可得

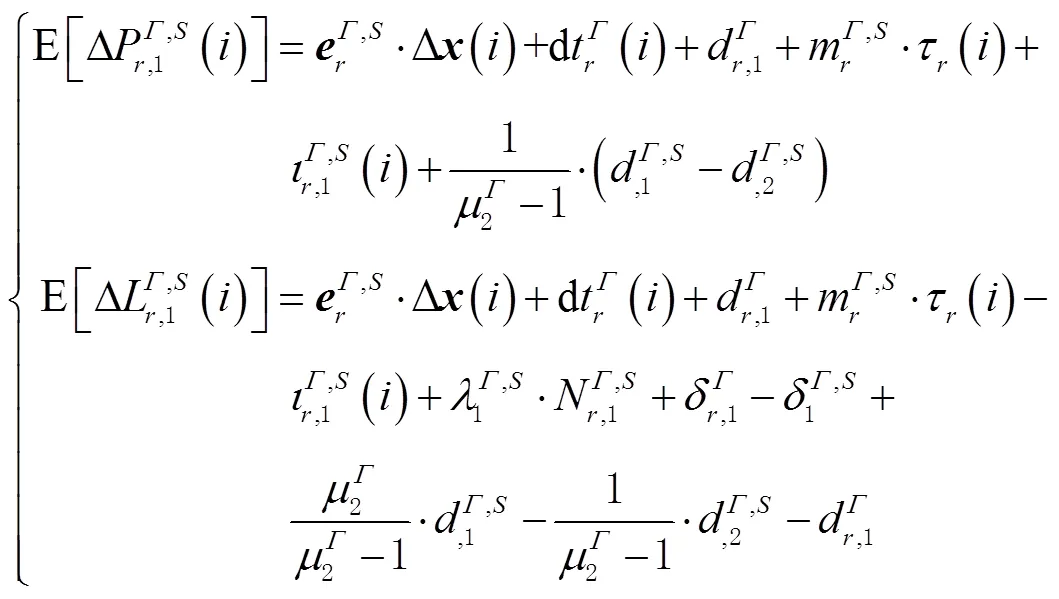
式（2）存在三类秩亏，各参数无法独立可估，为此需要先消除方程中的秩亏。首先，针对第一类，接收机钟差、接收机和卫星码/相位偏差、电离层延迟和模糊度之间的秩亏，进行参数重组后可得到：

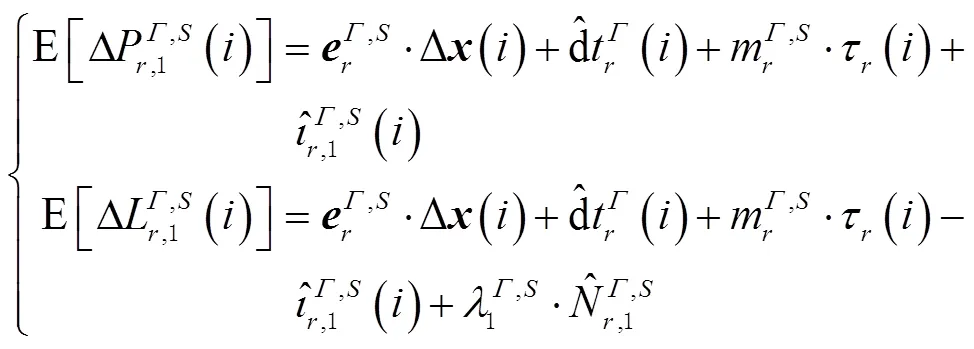
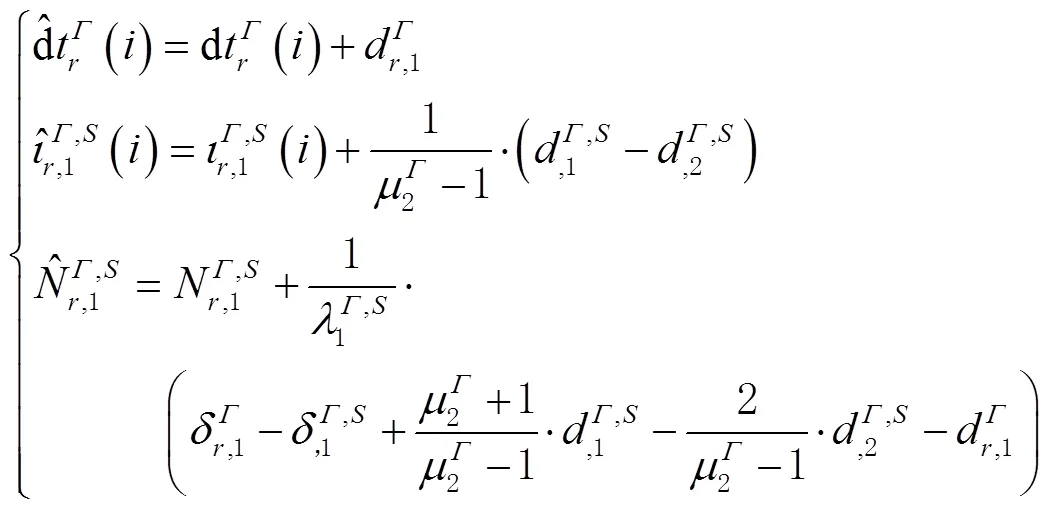
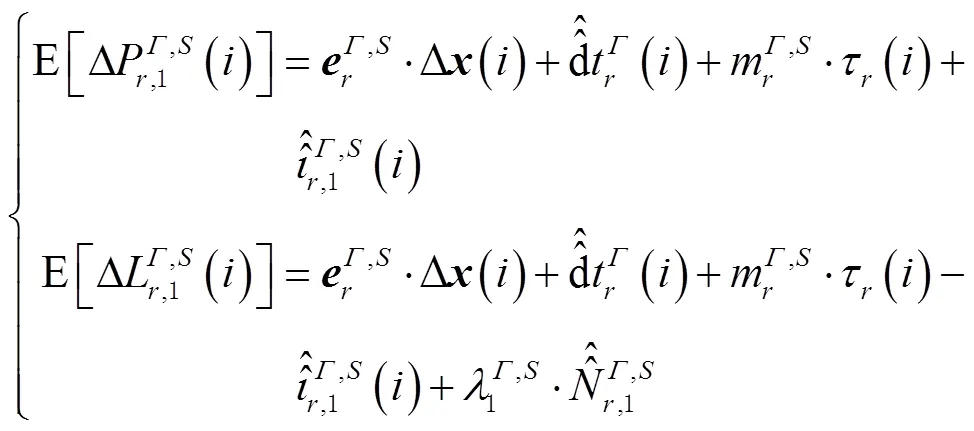
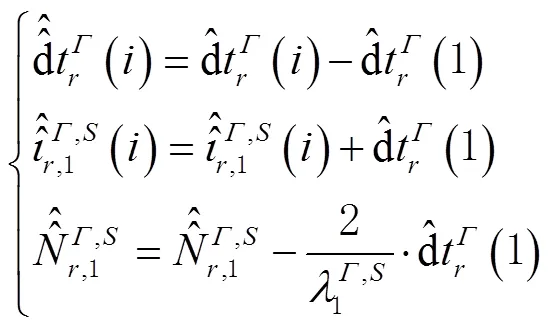
式（5）中，由于首历元方程个数小于待估参数的个数，存在第三类秩亏。对此，须联合前2个历元观测值构成观测方程来启动滤波器。至此，满秩的单频非组合PPP模型可表达为

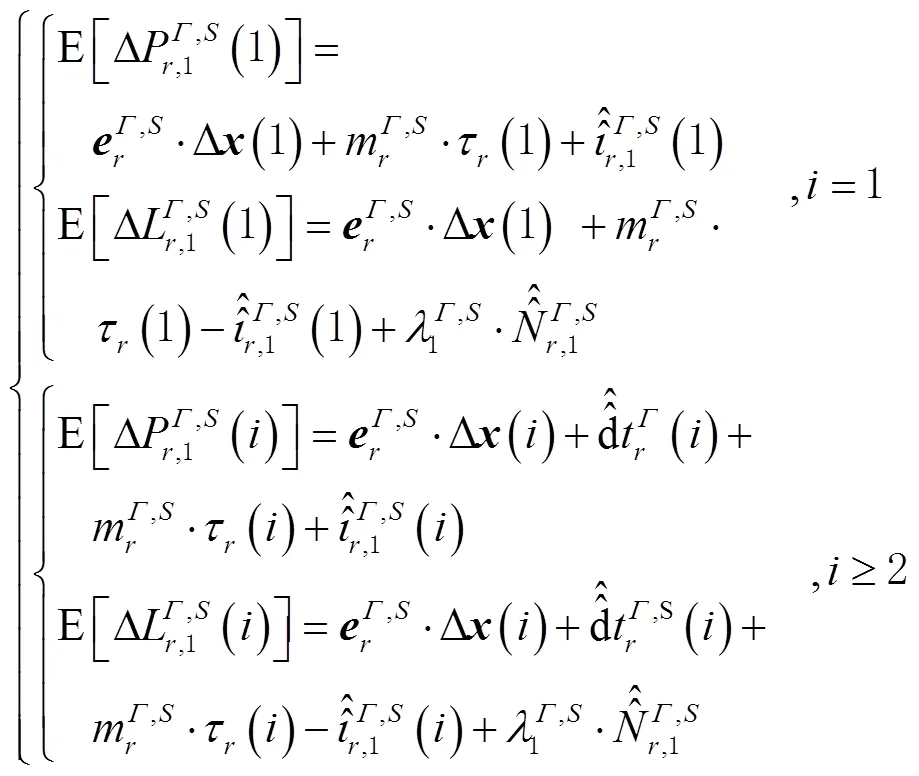
由式（5）和式（6）可看出，待估参数为有偏的接收机钟差、有偏的电离层斜延迟和有偏的相位模糊度。其中接收机钟差吸收了接收机端的码偏差和首历元接收机钟差，实际估值为相对于首历元接收机钟差的变化量。有偏的电离层斜延迟吸收了卫星端的码偏差和来自IGS精密卫星钟差产品的卫星码偏差及首历元接收机钟差，可用于电离层建模[16]。重参数化的模糊度吸收了各类偏差和首历元接收机钟差，因此丧失了整数特性。

1.1.2 单频非组合电离层加权模型

对于单频电离层加权PPP模型，通常采用外部电离层产品（如IGS发布的全球电离层产品（global ionosphere map，GIM））等作为伪观测值，结合式（2）可得

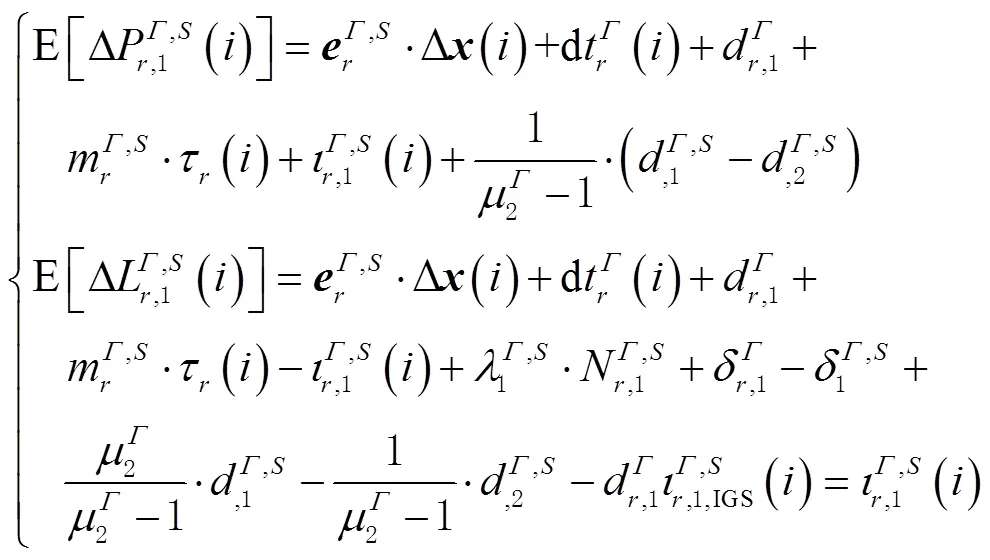
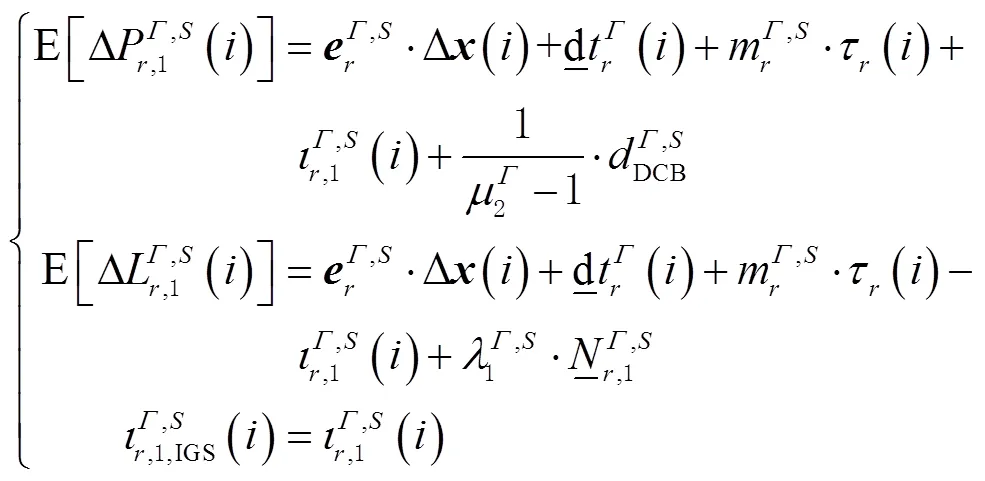
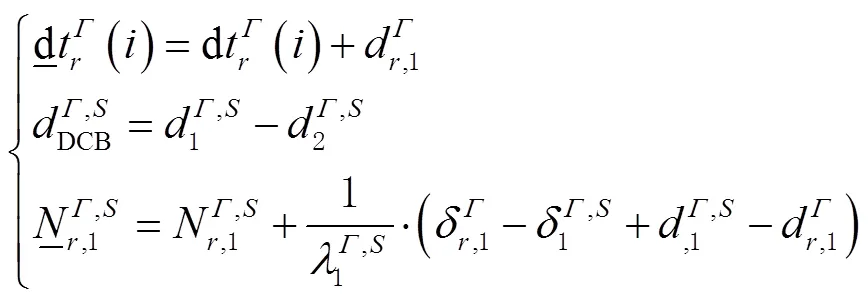
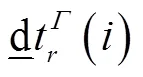
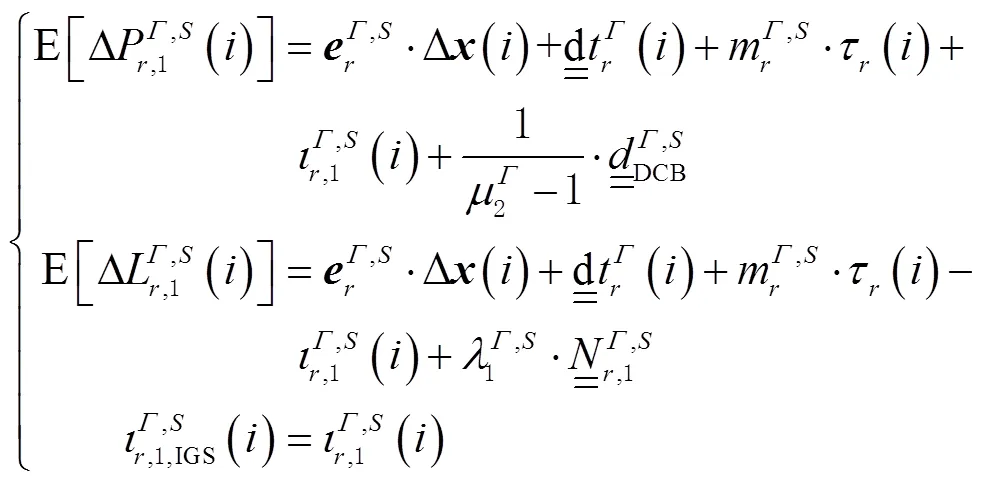
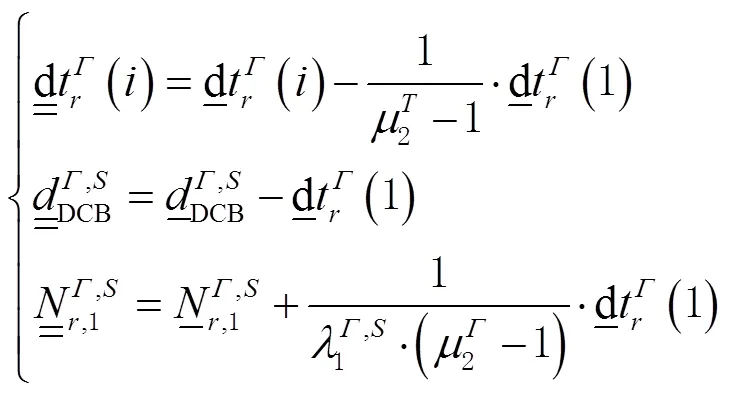
1.2 多频多模非组合PPP模型

在GNSS中，GPS、Galileo和BDS采用码分多址（code division multiple access, CDMA）信号播发技术，而GLONASS采用频分多址（frequency division multiple access, FDMA）播发技术，不同的卫星使用不同的频率。笔者将非组合PPP模型先根据GNSS信号体制分为CDMA模型和FDMA模型2类分开介绍，最后给出模型的统一表达形式。

1.2.1 多频CDMA模型

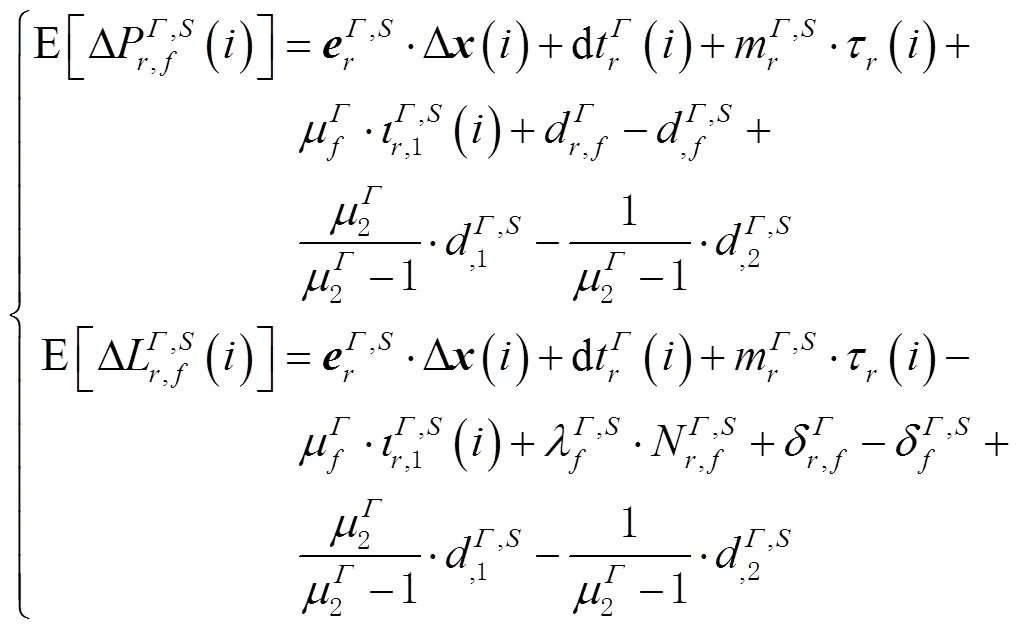
式（13）中，各待估参数间存在多类秩亏，如接收机钟差、接收机码偏差和电离层延迟间的秩亏等，无法独立求解。为此，笔者采用参数重组策略，重参数化感兴趣的参数，依次消除方程中的秩亏，最后得到满秩的方程为

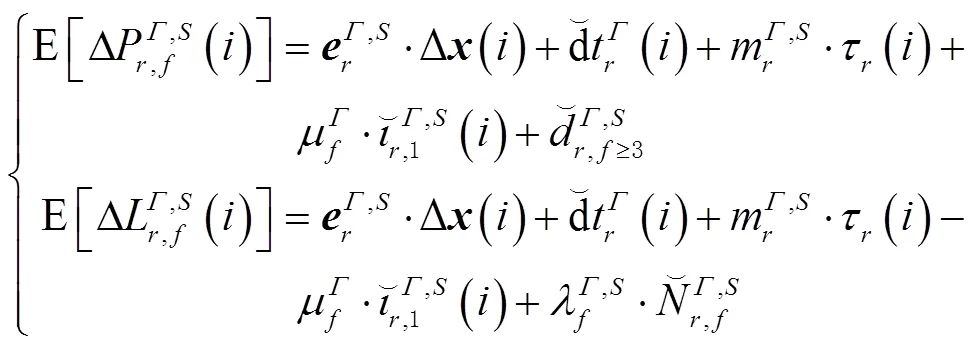
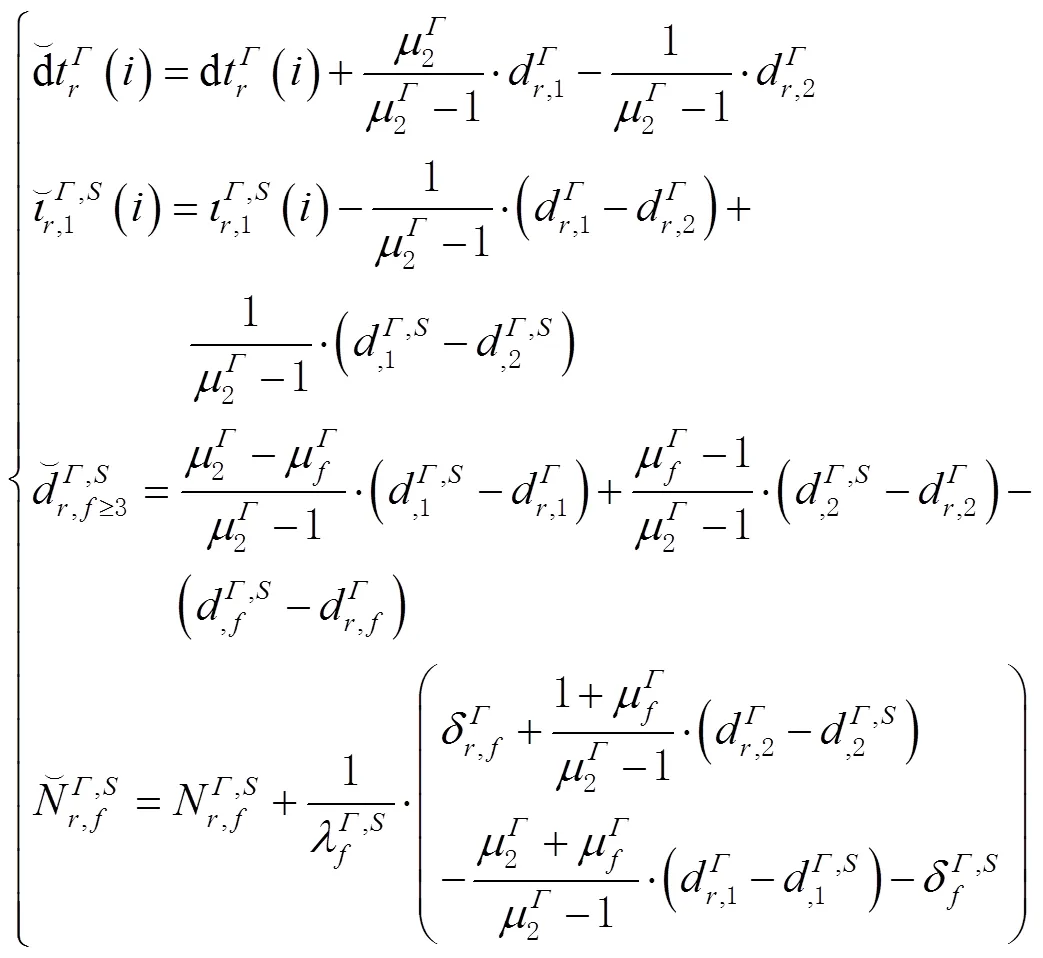
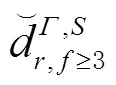
1.2.2 多频FDMA模型

不同于CDMA信号体制，GLONASS通过不同的信号频率来区分不同卫星，这种技术称为FDMA技术。不同的频率信号在接收机内部产生的硬件延迟并不一致，这导致了频率间偏差（inter-frequency bias, IFB）。IFB同时存在于伪距和载波相位观测值中，对于精密定位而言，其造成的误差不可忽略[18]。为此，严密考虑IFB的影响后，GLONASS伪距和载波相位观测方程为

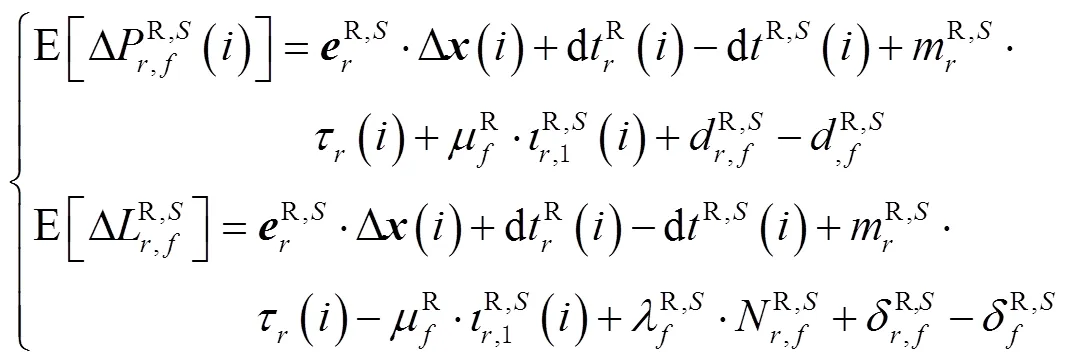
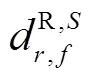
接收机相位偏差在浮点解时会被相位模糊度吸收，不会对定位产生不利影响；而伪距IFB量级较大，对定位会造成不利影响，因此须严密考虑[19-21]。对于GLONASS精密定位，伪距IFB处理方式可分为三类：其一是忽略IFB的影响，并对伪距观测值降权处理，部分伪距IFB会被伪距残差所吸收[22-23]；其二是通过标定好的IFB对伪距观测值进行改正，研究表明该方法能提高定位的收敛速度，但该方法需要事先标定，降低了数据处理效率[24]；其三是将伪距IFB作为待估参数和其他参数一起估计，该方式会引入过多的待估参数，降低模型的强度，甚至会引起秩亏，一般用于多系统数据联合处理中[23,25]。另有研究表明，伪距IFB与频率号存在近似的线性关系[20]，本文以此为假设来模型化伪距IFB，即

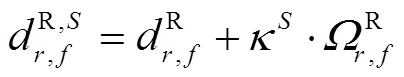
将式（17）代入式（16）中，并考虑IGS的精密卫星钟差产品改正，此时，非组合PPP模型中，不仅存在CDMA模型中秩亏，还存在引入伪距IFB而造成的秩亏。为此，采用与CDMA模型类似的参数重组方法，依次消除各类秩亏，推导过程为

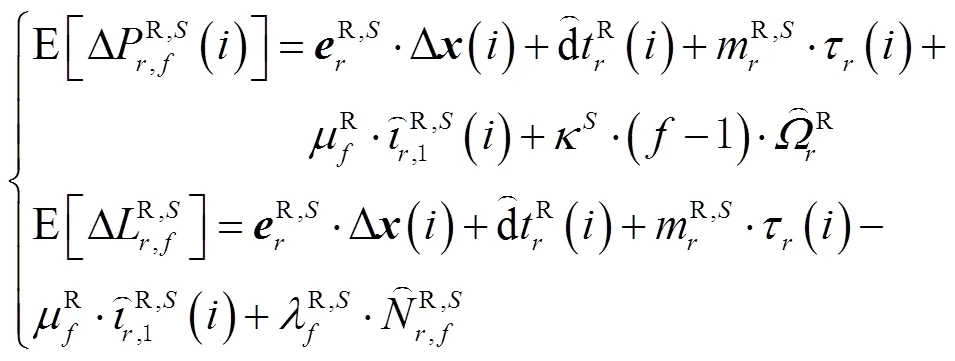
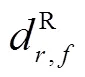
1.2.3 多模GNSS非组合PPP模型

前文已分别构建满秩的CDMA和FDMA非组合PPP模型，在此基础上，联合式（14）和式（18），并考虑卫星系统间偏差（inter system bias, ISB），即可得到GPS、GLONASS、Galileo和BDS联合处理观测方程[12,26]，即

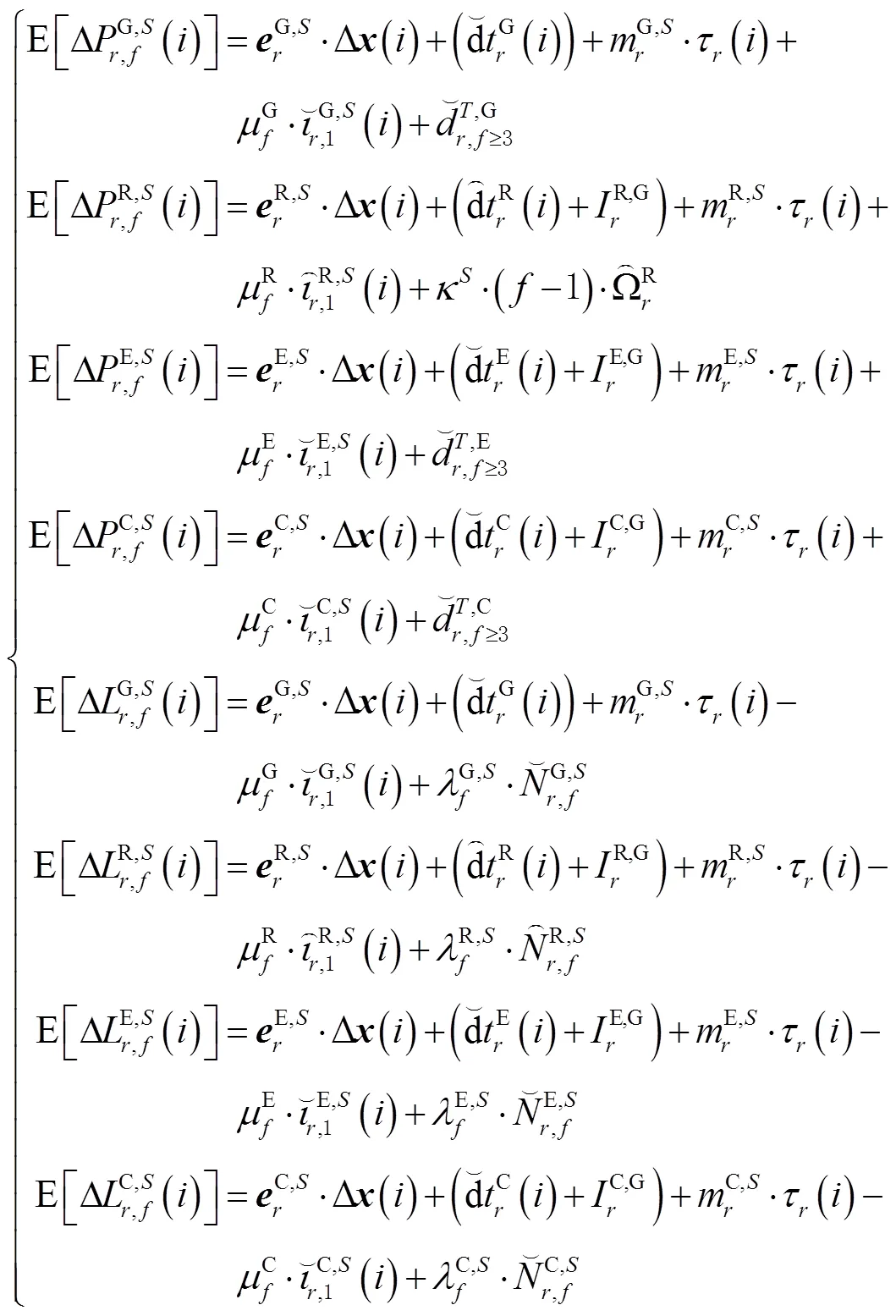
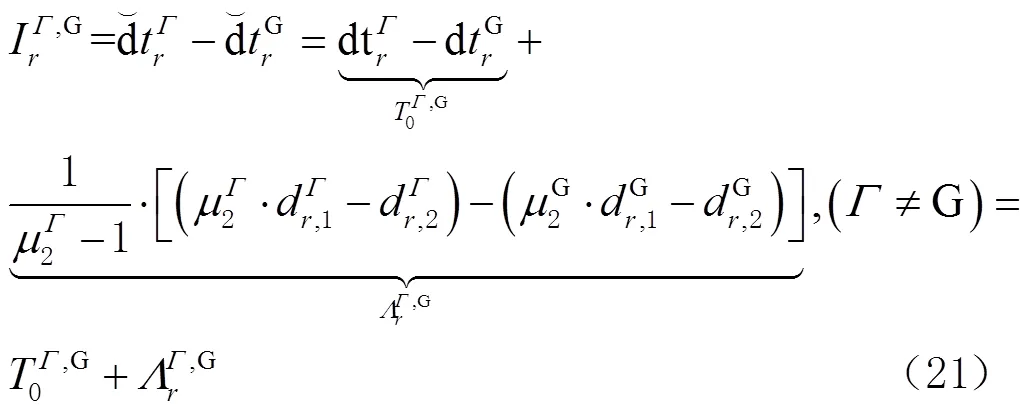
综上所述，式（20）所示的GPS/GLONASS/ BDS/Galileo四系统非组合PPP模型中的待估参数向量为

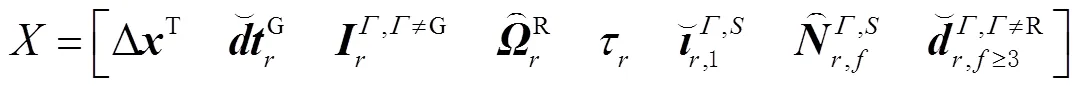
1.3 精化的非组合PPP模型

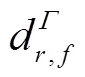
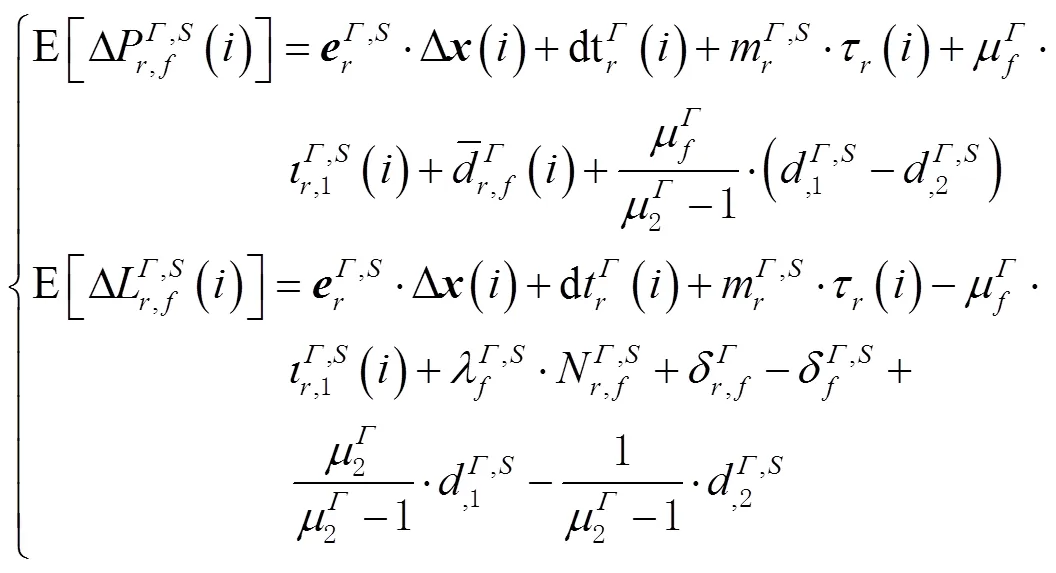
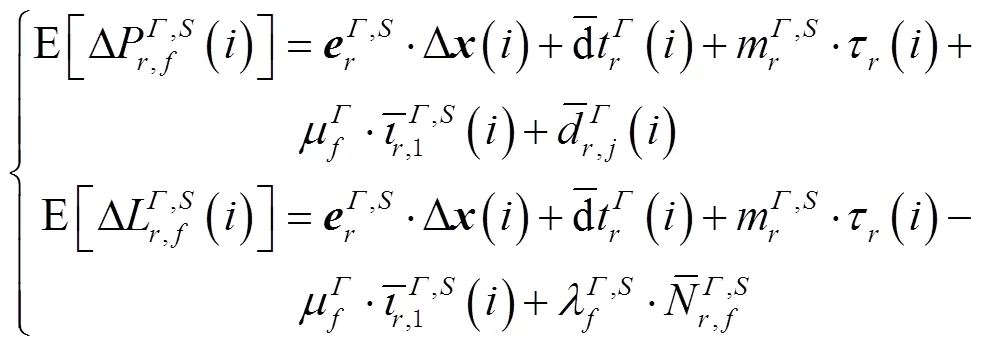
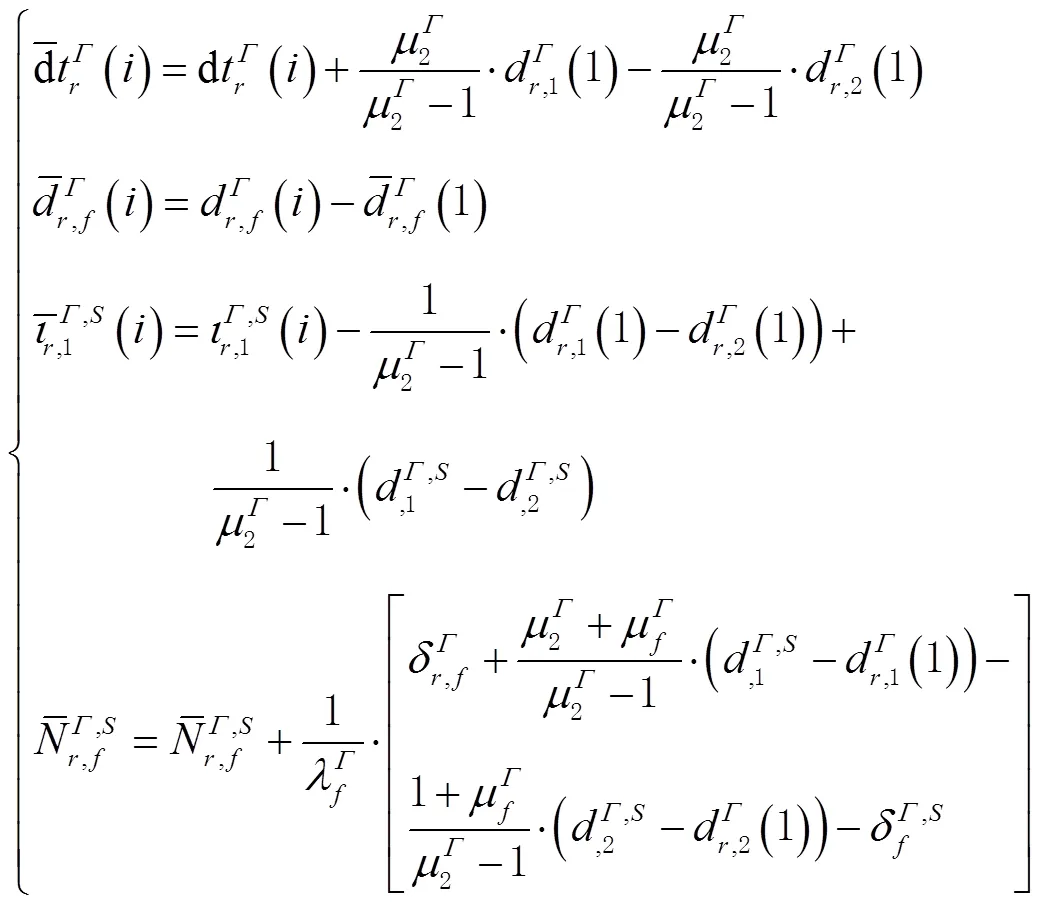
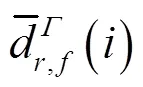
2 非组合PPP的应用

前文系统总结了从单频到多频的非组合PPP模型和算法，得益于非组合PPP模型的优势，可直接估计卫星至接收机视线方向的电离层斜延迟，拓展了其在空间大气等方面的应用。后文将全面介绍非组合PPP在包括电离层建模在内的相关应用。

2.1 电离层提取

非组合PPP与传统消电离层组合PPP相比最大的区别就是其将电离层斜延迟作为未知参数进行高精度估计，这意味着非组合PPP可为GNSS高精度电离层建模提供一种新的解决方案。基于GNSS电离层建模的关键是获取电离层观测值。目前，基于GNSS获取电离层观测值的主流方法是载波相位平滑码（code to carrier levelling, CCL）方法[31]。该方法通过逐历元形成无几何组合伪距和载波相位观测值的方式消除大量待估参数并保留了原始观测数据的信息，然后再通过（加权）平均的方式削减连续卫星弧段中无法消除的伪距多路径和观测噪声等提取电离层观测值。然而，该方法得到的电离层观测值即便进行了平滑处理，仍难以消除与测站有关的误差。且其完全消除了卫星间参数的相关性，采用逐卫星逐弧段的处理方式，这种方式对于短弧段观测或低高度角卫星，其所受测站相关误差的影响更大。相比于上述传统电离层提取方案，非组合PPP可很好地克服其缺陷。首先，由于非组合PPP对几何项的分解，使得各卫星参数具有相关性，对于所有卫星参数统一平差处理，高质量卫星信息可对低质量卫星产生贡献而解决单颗卫星质量差的问题。另外，非组合PPP可合理利用高精度的精密轨道、钟差产品增强模型强度，从而提高电离层观测值的精度。针对于此，文献[32]系统地对比了非组合PPP与CCL所提取电离层观测值的性能[32]，用零、短基线获取站间单差的方式揭示了CCL易受多路径效应和观测噪声影响的缺陷，并验证了非组合PPP技术提取的电离层斜延迟可大大削弱上述2种误差的影响。

非组合PPP所估计出的电离层观测值同CCL所得到的电离层观测值相同，由斜向电离层总电子含量(slant total electric content, sTEC)和站星差分码偏差DCB组成，因此需要从电离层观测值将二者分离开。电离层建模中，通常要将sTEC通过投影函数转化为垂向电离层总电子含量（vertical total electric content, vTEC）。基于电离层薄层假设sTEC与vTEC的关系如图1所示[33]。利用电离层建模常用的数学模型对vTEC进行数学表达后，结合图1中的投影关系并根据需要加入零均值约束后，即可求得vTEC与DCB参数。文献[5]说明了非组合PPP电离层观测值得到的vTEC相比于基于CCL求解的vTEC具有更高的精度和更快的收敛速度，基于非组合PPP求解的vTEC的平滑性与变化规律均与已知的电离层特性吻合，验证了非组合PPP在电离层建模方面的有效性和可靠性。

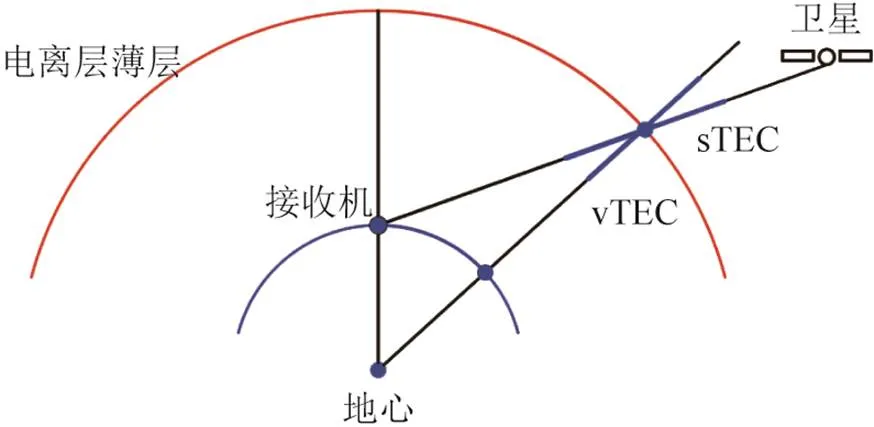
图1 电离层薄层假设及vTEC、sTEC转换

上述非组合PPP电离层建模的应用均需要事后精密产品的支撑，无法用于电离层实时建模与实时监控。为了支持实时精密单点定位等实时应用，IGS于2011年提出以状态空间表达（state space representation, SSR）信息的形式对外播发各类实时产品，包括轨道、钟差等。用户可实时获取到精度优于5 cm的精密卫星轨道以及标准偏差（standard bias, STD）优于0.12 ns的精密卫星钟差[34]。这为实时非组合PPP的研究以及实时电离层建模奠定了基础。图2展示了实时非组合PPP电离层建模的流程。文献[3]选取了均匀分布于澳大利亚区域的30个亚洲-太平洋参考框架（Asia-Pacific reference frame, APREF）测站，利用实时非组合PPP对澳大利亚地区进行实时电离层建模实验。基于SSR校正以及实时SSR解码软件IGGNtrip实现了澳大利亚地区实时格网vTEC的生成[35]。与CCL法相比，非组合PPP技术所提取的sTEC用于vTEC建模后的平均均方根误差（root mean square error, RMS）分别为0.91和1.09个总电子含量单位（total electron content unit, TECU）。从函数模型和实际提取精度上证明了实时非组合PPP算法电离层延迟提取的优越性。

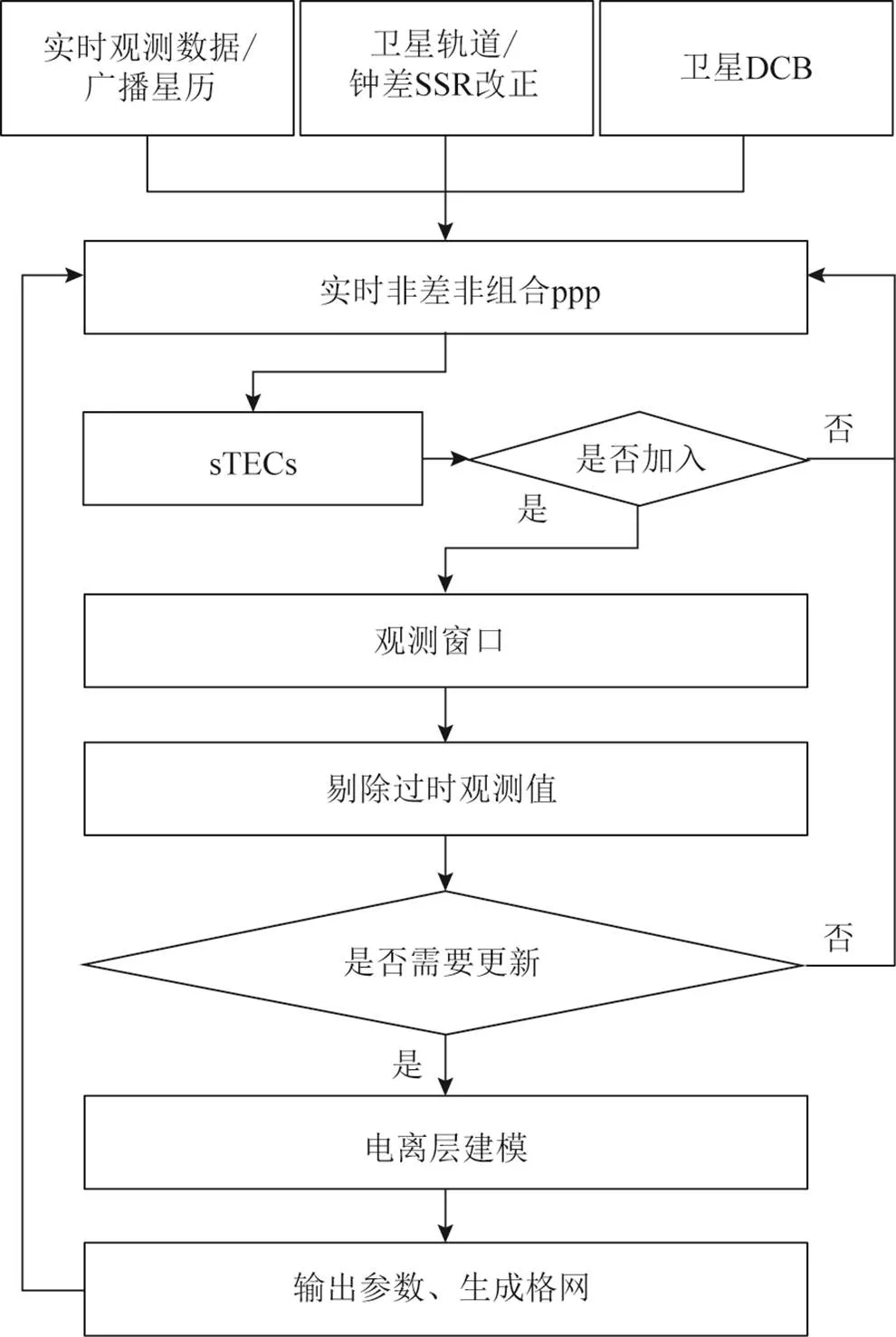
图2 实时非组合PPP电离层建模流程

2.2 单/多频非组合PPP应用拓展

为了满足低成本大众用户高精度应用需求，提出基于单频的非组合PPP算法[16]。由于单频PPP的非组合特性，模型中仍包含电离层参数，因此，单频非组合PPP也可为空间大气反演提供一种有效的高精度单频解决方案。单频非组合PPP满秩模型的推导与双频非组合PPP算法有所不同，经参数重组后会出现行秩亏，因此必须联合前2个历元的观测数据才能启动滤波器。此外，在消除秩亏的过程中，待估参数的可估形式有所不同。单频非组合PPP满秩模型中的电离层参数吸收了首历元的接收机钟差和卫星码偏差。因此需要注意的是，若数据出现中断，由于新的接收机钟差被引入作为第一历元接收机钟差，结果也会出现跳变。从单频PPP电离层观测值提取vTEC的方式与前文所述一致，均采用合适的电离层建模方案。文献[36]详细推导了单频非组合PPP的函数模型并利用单频非组合PPP进行了电离层反演以及水汽反演。表明了单频非组合PPP所提取的vTEC精度可达2.5个TECU左右，精度与基于双频的CCL法相当，且其所提取的水汽与无线探空仪数据相比，精度在3 mm以内。这也验证了单频非组合PPP能够有效地为空间大气研究领域提供一种高精度低成本的解决方案[37-39]。

除了满足单频低成本的应用需求，GNSS多频数据是未来的发展趋势，大量学者围绕多频多模GNSS模型算法及应用开展了研究，取得了丰硕的成果。文献[4]详细推导了多频非组合PPP的函数模型。多频非组合PPP模型与双频模型基本一致，不同的是，多频非组合PPP满秩函数模型包含了一项新参数，该参数为第一、二频点与第一、其他频带站星DCB的线性组合。从多频非组合PPP满秩函数模型上看，其模型强度更高。表1列举了CCL法、单频非组合PPP法（SF-PPP）、双频非组合PPP法（dual-frequency PPP，DF-PPP）、三频非组合PPP法（trible-frequency PPP，TF-PPP）的观测信息，其中表示观测卫星数，表示历元数。多频非组合PPP的多余观测数显著大于其他模型，这也从理论上验证了多频观测值对于非组合PPP具有更高精度贡献。文献[4]所使用的多频非组合PPP电离层反演算法能灵活处理双频、三频甚至任意频率的GNSS信号，并利用该算法处理了来自IGS的400多个站，分别基于2014年（太阳活动强）和2018年（太阳活动弱）的数据进行vTEC的建模。与IGS的最终产品进行比较，2014年和2018年利用该方法所提取的全球vTEC的RMS值分别为1.84和1.23个TECU，优于IGS最终产品的标称精度。表明多频非组合PPP可以提供更高精度和更可靠的vTEC结果。

表1 各电离层斜延迟提取算法模型对比

2.3 基于非组合PPP的DCB估计

基于非组合PPP估计的电离层延迟中包含卫星频间偏差参数，经过模型化电离层延迟，使得sTEC与DCB分离。因此，DCB是电离层产品的副产品，也是GNSS中的一项重要参数。IGS利用球谐函数进行全球电离层建模的同时也向用户提供卫星DCB产品。同样地，非组合PPP在进行电离层参数估计的同时也可以向用户播发卫星DCB产品。针对非组合PPP所提供的DCB产品的质量与精度，也有学者做了大量的研究。文献[40]首先评估了非组合PPP所提取的站星DCB的精度，结果表明非组合PPP所提取的站星DCB精度优于基于CCL法得到的站星DCB。另外，文献[39]基于单频非组合PPP采用零均值约束分离了卫星DCB与测站DCB，提取了多系统的卫星DCB，并以欧洲定轨中心（Centre for Orbit Determination in Europe, CODE）提供的多系统卫星DCB产品为参考对其进行评估。得到的GPS/GLONASS P1-P2、BDS C2I-C7I、Galileo C1X-C5X卫星DCB精度分别为0.27、0.74、0.51和0.35 ns，验证了单频非组合PPP DCB估计的可行性。类似地，基于多频非组合PPP，也可得到卫星DCB且精度更高，文献[10]对于多频多模非组合PPP所提取的各系统各频率间的DCB进行了系统地评估，表2给出了所估计的各系统各频率间的DCB对比各机构（如德国宇航中心（Deutsches Zentrum für Luft- und Raumfahrt, DLR）、中国科学院（Chinese Academy of Sciences, CAS）、中国科学院测量与地球物理研究所（Institute of Geodesy and Geophysics, IGG）） DCB产品所得到的RMS结果。进一步表明该方法可以作为一种有效且准确的方法用于多频率和多GNSS环境下的全球vTEC建模和多GNSS DCB估计。

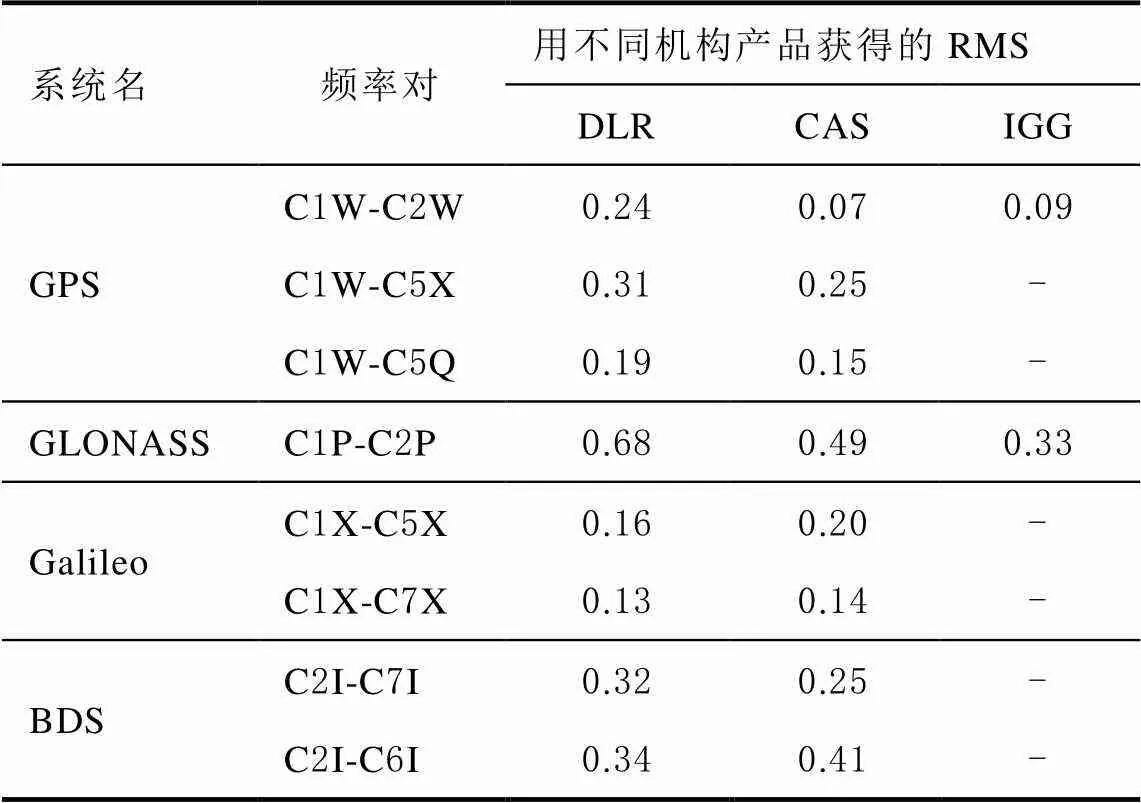
表2 多频多系统非组合PPP各频率对DCB估计结果 ns

3 精化的非组合PPP应用

在上文所描述的非组合PPP算法中，均认为算法所涉及的各类偏差，接收机码偏差（receiver code bias, RCB）为时不变参数。但大量的研究表明，卫星端各类偏差较为稳定，而接收机RCB由于接收机所处环境的变化（如环境温度），会出现较为显著的短时变化。在传统的非组合PPP满秩模型中，可估的电离层斜延迟包含了无几何组合接收机RCB，接收机钟差吸收了消电离层组合接收机RCB，且可估的模糊度也包含了接收机端RCB参数。若忽略这种短时变化，将会对这些参数的估计会造成负面影响。

非组合PPP和CCL方法所估计的电离层斜延迟参数形式一致，故CCL方法所得到的电离层结果也同样受到接收机端RCB短时变化的影响。因此顾及接收机偏差短时变化的算法首先应用于CCL方法中，文献[29]与文献[41]均揭示了接收机端码偏差短时变化及其与温度的强相关性。基于此，文献[42]提出了顾及RCB短时变化的改进CCL方法（modified CCL，MCCL）。使用MCCL后，所估算的TEC参数相比CCL法精度有明显提升。类似地，非组合PPP也可以通过考虑接收机RCB短时变化的方式改进电离层斜延迟参数的估计精度。这种顾及接收机偏差短时变化的非组合PPP方法也被称为改进的非组合PPP（modified PPP, MPPP）。由1.3节可知，与非组合模型相比，MPPP满秩模型中，接收机钟差、电离层可估形式均仅包含首历元的RCB，各频点上的RCB被当作参数独立估计，这有效避免了RCB短时变化对于其他参数估值的影响。

因此，MPPP模型会对电离层斜延迟、接收机钟差参数的估计产生贡献。这在文献[43]中被证明，对于sTEC参数，基于MPPP的sTEC的准确性相比基于PPP的sTEC提高了46%～96%。此外，接收机钟差参数的精准估计可以使得非组合PPP在精密授时领域得到更好的应用。结果表明，在顾及接收机短时变化的情况下，MPPP估计得到的接收机钟差的短、中、长期频率稳定性相对于PPP有显著提高，且可减少接收机钟差噪声，证实了MPPP具备较好的授时与时间传递能力。

4 结束语

本文首先回顾了GNSS精密单点定位模型算法的发展历程，详细介绍了单频非组合电离层浮点和电离层加权PPP模型、多频非组合CDMA和FDMA PPP模型及顾及接收机码偏差短时变化的MPPP模型，并采用参数重组策略，消除了方程中的秩亏，得出了可估的满秩函数模型及各参数的可估形式。并介绍了非组合PPP在对流延迟和电离层斜延迟提取、差分码偏差估计和精密授时方面等方面的应用。

算法模型方面，对于单频非组合PPP模型，可分为电离层浮点和电离层加权2类，二者参数的可估形式存在差异。电离层浮点中，电离层斜延迟被当作参数估计，而电离层加权模型通过内插的GIM产品引入了电离层斜延迟伪观测值。后者模型中，由于电离层伪观测值的加入，使得卫星差分码偏差可估。对于多频多模非组合PPP满秩模型而言，与单频满秩模型不同的是，多频多模PPP满秩模型首历元即可初始化滤波，无须联合前几个历元。同时，接收机钟差、电离层斜延迟和相位模糊度参数的可估形式有所差异。对于顾及接收机码偏差短时变化的MPPP模型，由于将接收机码偏差当作时变参数，故其秩亏类型和传统模型并不一致，但参数重组的过程类似。其中可估的接收机钟差和电离层斜延迟均仅包含了首历元的接收机码偏差，有效避免了接收机码偏差变化对估值的影响。

应用方面，构建的非组合单频电离层浮点模型为低成本设备的空间天气监测提供了理论支撑。实验结果表明了单频非组合PPP所提取的vTEC精度可达2.5个TECU左右，精度与基于双频数据提取结果相当；同时，提取的天顶对流延迟精度优于3 mm。多频多模PPP也用于DCB估计，实验表明其结果优于传统CCL方法。对于顾及RCB短时变化的MPPP，由于接收机钟差和电离层斜延迟参数可估形式包含的是首历元RCB，规避了时变RCB的影响。研究结果表明，MPPP提取的sTEC精度提升46%以上，时间传递具有更长期的稳定性。

基于现有的研究成果来看，非组合PPP理论算法已较为完善，非组合PPP在空间天气监测、卫星DCB估计和精密时间传递等方面得到较好的应用。然而，与传统消电离层组合PPP类似，非组合PPP初始化过长的短板使其始终无法走向实用阶段。为此，精密单点实时动态定位（PPP-RTK）技术应运而生。PPP-RTK技术主要有2种模，即非差组合PPP-RTK和非组合PPP-RTK。非差组合PPP-RTK首先基于消电离层组合观测方程和Melbourne-Wubbena组合观测方程估计精密卫星钟差及精密卫星码/相位偏差产品，再基于精密卫星产品利用非组合观测方程精密单点定位提取区域大气延迟精密产品。非组合PPP-RTK则通过严密的网端非组合观测方程同步估计精密卫星钟差、精密卫星码/相位偏差以及区域大气延迟精密产品。PPP-RTK技术的主要目标是实现单站用户快速精密定位。在单站用户定位中，服务端精密卫星轨道、精密卫星钟差及精密卫星码偏差是实现单站精密定位的关键，服务端精密卫星相位偏差是实现单站模糊度固定的关键，而精密电离层延迟产品则是加速模糊度固定的关键。其中，电离层延迟的估计、建模及传输是当前PPP-RTK技术亟待解决的关键问题。另一方面，低轨卫星是未来发展趋势，大量的低轨卫星，其卫星空间几何构型变化更快，能加速PPP收敛，但现有研究结果均为仿真数据结果，尚待进一步验证。总之，PPP的快速初始化和伴随的相关问题仍将是今后很长时间的研究内容。

[1] KOUBA J, HÉROUX P. Precise point positioning using IGS orbit and clock products[J]. GPS Solutions, 2001, 5(2): 12-28.

[2] ZUMBERGE J F, HEFLIN M B, JEFFERSON D C, et al. Precise point positioning for the efficient and robust analysis of GPS data from large networks[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B3): 5005-5017.

[3] LIU T, ZHANG B, YUAN Y, et al. Real-time precise point positioning (RTPPP) with raw observations and its application in real-time regional ionospheric VTEC modeling[J]. Journal of Geodesy, 2018, 92(11): 1267-1283.

[4] LIU T, ZHANG B, YUAN Y, et al. On the application of the raw-observation-based PPP to global ionosphere VTEC modeling: an advantage demonstration in the multi-frequency and multi-GNSS context[J]. Journal of Geodesy, 2020, 94(1): 1-20.

[5] 张宝成, 欧吉坤, 袁运斌, 等. 利用非组合精密单点定位技术确定斜向电离层总电子含量和站星差分码偏差[J]. 测绘学报, 2011, 40(4): 447-453.

[6] 张小红, 李星星, 李盼. GNSS精密单点定位技术及应用进展[J]. 测绘学报, 2017, 46(10): 1399-1407.

[7] 辜声峰. 多频GNSS非差非组合精密数据处理理论及其应用[D]. 武汉: 武汉大学, 2013: 131-163.

[8] GAO Y, SHEN X. Improving ambiguity convergence in carrier phase-based precise point positioning[C]//The Institute of Navigation. Proceedings of the 14th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GPS 2001). Salt Lake City, USA: the Institute of Navigation, Inc., 2001: 1532-1539[2022-05-24].

[9] 张宝成, 欧吉坤, 袁运斌, 等. 基于GPS双频原始观测值的精密单点定位算法及应用[J]. 测绘学报, 2010, 39(5): 478-483.

[10] LIU T, ZHANG B, YUAN Y, et al. Multi-GNSS triple-frequency differential code bias (DCB) determination with precise point positioning (PPP)[J]. Journal of Geodesy, 2018, 93(5): 765-784.

[11] 张宝成. GNSS非差分非组合精密单点定位的理论方法与应用研究[D]. 北京: 中国科学院研究生院, 2012: 55-71.

[12] 刘腾. 多模GNSS非组合精密单点定位算法及其电离层应用研究[D]. 北京: 中国科学院大学, 2017: 37-61.

[13] KHODABANDEH A, TEUNISSEN P J G. Integer estimability in GNSS networks[J]. Journal of Geodesy, 2019, 93(9): 1805-1819.

[14] ODIJK D, ZHANG B, KHODABANDEH A, et al. On the estimability of parameters in undifferenced, uncombined GNSS network and PPP-RTK user models by means of S-system theory[J]. Journal of Geodesy, 2015, 90(1): 15-44.

[15] XIANG Y, CHEN X, PEI L, et al. On enhanced PPP with single difference between-satellite ionospheric constraints[J]. Navigation, 2022, 69(1): 1-18.

[16] ZHANG B, TEUNISSEN P J G, YUAN Y, et al. Joint estimation of vertical total electron content (VTEC) and satellite differential code biases (SDCBs) using low-cost receivers[J]. Journal of Geodesy, 2017, 92(4): 401-413.

[17] LEICK A, RAPOPORT L, TATARNIKOV D. GPS satellite surveying[M]. New Jersey, USA:John Wiley & Sons, Inc., 2015: 92-169.

[18] KOZLOV D, TKACHENKO M, TOCHILIN A. Statistical characterization of hardware biases in GPS+GLONASS receivers[C]//The Institute of Navigation.Proceedings of the 13th International Technical Meeting of The Satellite Division of The Institute of Navigation (ION GPS 2000). Salt Lake City, USA: The Institute of Navigation, Inc., 2000: 817-826[2022-05-24].

[19] AL-SHAERY A, ZHANG S, RIZOS C. An enhanced calibration method of GLONASS inter-channel bias for GNSS RTK[J]. GPS Solutions, 2013, 17(2): 165-173.

[20] WANNINGER L. Carrier-phase inter-frequency biases of GLONASS receivers[J]. Journal of Geodesy, 2012, 86(2): 139-148.

[21] YAMADA H, TAKASU T, KUBO N, et al. Evaluation and calibration of receiver inter-channel biases for RTK-GPS/GLONASS[C]//The Institute of Navigation. Proceedings of the 23rd International Technical Meeting of The Satellite Division of the Institute of Navigation (Ion GNSS 2010). Portland, USA: the Institute of Navigation, Inc., 2010: 1580-1587.

[22] CAI C, GAO Y. Precise point positioning using combined GPS and GLONASS observations[J]. Positioning, 2007, 1(11): 13-22.

[23] CAI C, GAO Y. Modeling and assessment of combined GPS/GLONASS precise point positioning[J]. GPS Solutions, 2013, 17(2): 223-236.

[24] CHUANG S, WENTING Y, WEIWEI S, et al. GLONASS pseudorange inter-channel biases and their effects on combined GPS/GLONASS precise point positioning[J]. GPS Solutions, 2013, 17(4): 439-451.

[25] LOU Y, ZHENG F, GU S, et al. Multi-GNSS precise point positioning with raw single-frequency and dual-frequency measurement models[J]. GPS Solutions, 2016, 20(4): 849-862.

[26] LIU T, YUAN Y, ZHANG B, et al. Multi-GNSS precise point positioning (MGPPP) using raw observations[J]. Journal of Geodesy, 2016, 91(3): 253-268.

[27] MERVART L, WEBER G. Real-time combination of GNSS orbit and clock correction streams using a Kalman filter approach[C]//The Institute of Navigation.Proceedings of the 24th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2011). Portland, USA: the Institute of Navigation, Inc., 2011: 707-711[2022-05-24].

[28] CHOY S, ZHANG S, LAHAYE F, et al. A comparison between GPS-only and combined GPS+ GLONASS Precise Point Positioning[J]. Journal of Spatial Science, 2013, 58(2): 169-190.

[29] ZHA J, ZHANG B, YUAN Y, et al. Use of modified carrier-to-code leveling to analyze temperature dependence of multi-GNSS receiver DCB and to retrieve ionospheric TEC[J]. GPS Solutions, 2019, 23(4): 1-12.

[30] ZHANG B, ZHAO C, ODOLINSKI R, et al. Functional model modification of precise point positioning considering the time-varying code biases of a receiver[J]. Satellite Navigation, 2021, 2(1): 1-10.

[31] CIRAOLO L, AZPILICUETA F, BRUNINI C, et al. Calibration errors on experimental slant total electron content (TEC) determined with GPS[J]. Journal of Geodesy, 2007, 81(2): 111-120.

[32] 张宝成, 欧吉坤, 李子申, 等. 利用精密单点定位求解电离层延迟[J]. 地球物理学报, 2011, 54(4): 950-957.

[33] SCHAER S. Mapping and predicting the Earth's ionosphere using the global positioning system[J]. Geodätisch-Geophysikalische Arbeiten in der Schweiz, 1999,59: 1-205.

[34] KAZMIERSKI K, SOŚNICA K, HADAS T. Quality assessment of multi-GNSS orbits and clocks for real-time precise point positioning[J]. GPS Solutions, 2017, 22(1): 1-12.

[35] 贺伟欣. GNSS 实时数据获取与精密单点定位研究[D]. 北京:中国科学院大学,2015: 21-34.

[36] ZHAO C, YUAN Y, ZHANG B, et al. Ionosphere sensing with a low-cost, single-frequency, multi-GNSS receiver[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(2): 881-892.

[37] LI M, ZHANG B, YUAN Y, et al. Single-frequency precise point positioning (PPP) for retrieving ionospheric TEC from BDS B1 data[J]. GPS Solutions, 2018, 23(1): 1-11.

[38] ZHAO C, ZHANG B, LI W, et al. Simultaneous retrieval of PWV and VTEC by low-cost multi-GNSS single-frequency receivers[J]. Earth and Space Science, 2019, 6(9): 1694-1709.

[39] ZHAO C, ZHANG B, ODOLINSKI R, et al. Combined use of single-frequency data and global ionosphere maps to estimate BDS and Galileo satellite differential code biases[J]. Measurement Science and Technology, 2020, 31(1) 015002.

[40] ZHANG B, OU J, YUAN Y, et al. Extraction of line-of-sight ionospheric observables from GPS data using precise point positioning[J]. Science China Earth Sciences, 2012, 55(11): 1919-1928.

[41] ZHANG X, ZHANG B, YUAN Y, et al. A refined carrier-to-code levelling method for retrieving ionospheric measurements from dual-frequency GPS data[J]. Measurement Science and Technology, 2020, 31(3): 035010.

[42] ZHANG B, TEUNISSEN P J G, YUAN Y, et al. A modified carrier-to-code leveling method for retrieving ionospheric observables and detecting short-term temporal variability of receiver differential code biases[J]. Journal of Geodesy, 2018, 93(1): 19-28.

[43] ZHANG B, ZHAO C, ODOLINSKI R, et al. Functional model modification of precise point positioning considering the time-varying code biases of a receiver[J]. Satellite Navigation, 2021, 2(1): 1-10.

Model algorithm and applications of uncombined precise point positioning for GNSS

ZHANG Baocheng1,3, LIU Teng1, XU Li1,2, GAO Rui1,2

（1. State Key Laboratory of Geodesy and Earth's Dynamics, Innovation Academy for Precision Measurement Science and Technology, Chinese Academy of Sciences, Wuhan 430077, China;2. University of Chinese Academy of Sciences, Beijing 100049, China;3. State Key Laboratory of Satellite Navigation System and Equipment Technology, the 54th Research Institute of China Electronics Technology Group Corporation, Shijiazhuang 050002, China）

In order to further develop the technology of uncombined precise point positioning (PPP) for global navigation satellite system (GNSS), the paper studied on the algorithm and its application: the full-rank function models of un-combined PPP from single frequency to multi-frequency and from a single constellation to multi-constellation were constructed, and the strategy of the rank defect elimination and parameter forms of uncombined PPP models were introduced; then combined with the characteristics of uncombined PPP technology, its typical applications in extraction of tropospheric delay and ionospheric delay, estimation of difference code bias, and precise timing were discussed; finally, in view of the latest development state, the future growing trend of undifferenced uncombined PPP technology was prospected.

global navigation satellite system(GNSS); BeiDou satellite navigation system (BDS); uncombined precise point positioning (PPP); short term variation of code bias

P228

A

2095-4999(2023)02-0001-12

张宝成, 刘腾, 徐黎, 等. GNSS非组合精密单点定位模型算法与应用[J]. 导航定位学报, 2023, 11(2): 1-12.（ZHANG Baocheng, LIU Teng, XU Li, et al. Model algorithm and applications of uncombined precise point positioning for GNSS[J]. Journal of Navigation and Positioning, 2023, 11(2): 1-12.）DOI:10.16547/j.cnki.10-1096.20230201.

2022-06-13

国家自然科学基金项目（42174034）；湖北省自然科学基金项目（2020CFA048）。

张宝成（1985—），男，安徽亳州人，博士，研究员，研究方向为GNSS非差非组合数据处理理论、算法及应用。