顾及共模误差的陆态网络GPS观测数据噪声分析

张 沛，魏冠军，雷传金，高茂宁

顾及共模误差的陆态网络GPS观测数据噪声分析

张 沛，魏冠军，雷传金，高茂宁

（兰州交通大学 测绘与地理信息学院/地理国情监测技术应用国家地方联合工程研究中心/甘肃省地理国情监测工程实验室，兰州 730070）

为了进一步研究共模误差的提取对分析全球定位系统（GPS）坐标时间序列最优噪声模型及速度场的影响，提出一种顾及共模误差的陆态网络GPS观测数据噪声分析方法：以西北地区70个陆态网络连续站10 a GPS观测数据为研究对象，利用主成分分析法剔除残差坐标时间序列中的共模误差；然后根据贝叶斯信息准则数值分析法对比分析滤波前后坐标时间序列最优噪声模型及速度场变化。结果表明，滤波前西北地区整体最优噪声模型以白噪声+闪烁噪声（WN+FN）组合模型为主，滤波后最优噪声模型仍以WN+FN为主，但部分站点滤波后最优噪声模型发生了变化；滤波后北（N）、东（E）、天（U）各分量速度不确定度可分别平均降低38.97%、36.36%、48.14%，水平速度场及垂向速度场精度均高于滤波前；主成分分析法（PCA）剔除共模误差可有效降低白噪声和有色噪声量级。

共模误差；坐标时间序列；主成分分析；贝叶斯信息准则；噪声模型

0 引言

全球定位系统（global positioning system，GPS）的区域监测网受海潮及大气负荷、地壳运动、气候变化等因素的影响，导致连续GPS站坐标时间序列中存在与时空相关的误差，称为共模误差（common mode error，CME）。许多学者对于CME的提取进行了大量研究，常用的滤波方法有堆栈法、主成分分析法（principal component analysis，PCA）、独立分量分析法（independent component analysis，ICA）、卡尔胡宁-勒夫展开法（Karhunen-Loève expansion，KLE）等方法[1-2]。文献[3]首次提出利用区域叠加滤波法提取并剔除共模误差；文献[4]对安徽省19个连续运行参考站（continuously operating reference stations，CORS）坐标时间序列采用主成分分析法进行空间滤波，滤波后噪声模型仍以白噪声+闪烁噪声为主；文献[5]对比分析了区域叠加法和主成分分析法，结果表明2种方法滤波效果极为接近，与数据的缺失率有很大关系；文献[6]对西南极区域24个GPS基准站采用PCA与ICA分析方法进行空间滤波，PCA能够有效提取区域GPS观测网中的共模误差。

西北地区构造运动强烈，气候复杂多变，陆态网数据为共模误差对噪声模型及速度场的影响相关研究提供了保障。本文针对西北地区包括新疆、青海、甘肃、宁夏、陕西（行政区域规划）5个省份共70个陆态网络连续站，选取2011—2021年10 a的观测数据分析研究，对原始数据进行预处理后利用PCA提取210个分量上的共模误差，对比分析滤波前后共模误差对坐标时间序列噪声特性及测站速度的影响。

1 GPS站坐标时间序列获取

1.1 数据来源

本文所使用的数据来自中国地震局全球卫星导航系统（global navigation satellite system，GNSS）数据产品服务中心平台(http://www. cgps.ac.cn)。其对数据的解算采用的是加米特（GAMIT）/格洛布克（GLOBK）软件，并与众多参数作平差估计来获得原始坐标时间序列。选取西北地区陆态网络连续站共70个站进行研究，站点分布如图1所示。

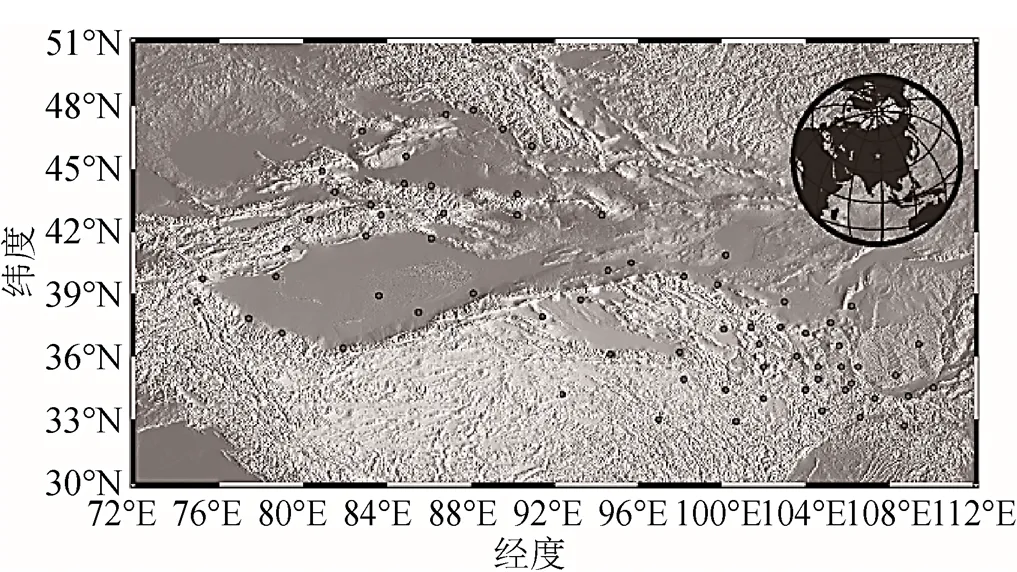
图1 西北地区陆态网络连续站站点分布

1.2 残差时间序列获取及预处理

受各种因素的影响，原始时序中难免会存在粗差及缺失值，因此在获取到原始坐标时间序列后，首先采用最小二乘法来拟合出其中的趋势项，包括线性趋势，利用式（1）获取残差时间序列；利用四分位距法来探测粗差，剔除奇异值，进而拟合出新的残差时间序列。GPS坐标时间序列的一般参数模型[7-9]为

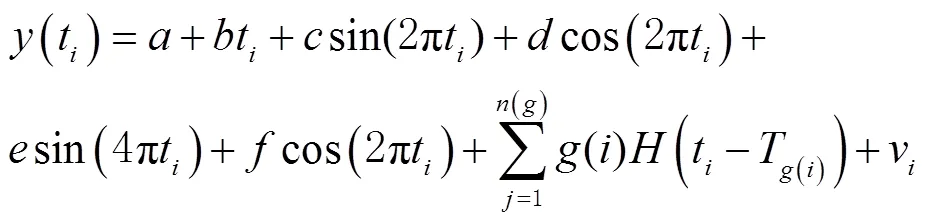
由于在PCA滤波前要确保时间序列的均匀采样，因此需要对残差坐标时间序列进行缺失值的插补。本文采用基于克里金-卡尔曼滤波器（Kriged Kalman filter，KKF）的动态时空插值方法[10]，其插值效果较为稳定，与连续缺失的比例关系不大；利用KKF动态插值的关键问题在于缺失数据随机出现并保持持续输出。假设在时刻的KKF观测方程为

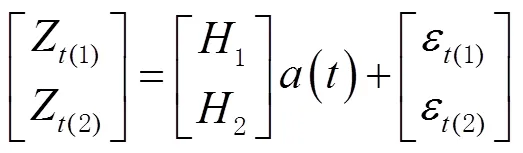
式中：、、分别为观测数据、观测数据的空间场和噪声；、、分别为缺失数据、缺失数据的空间场及噪声；在空间域上利用KKF观测方程通过克里金法插值缺失的数据并通过自回归模型在时间域上对其进行预测，最后将空域插值结果与时域预测结果相结合得到时空预测结果。图2为QHYS站不同分量插值前后的结果。

2 共模误差提取

为了提高站点坐标解算精度，必须对坐标时间序列中的共模误差进行剔除[11]。PCA滤波法是一种线性降维的方法，可以利用较少的数据维度来保证更多的数据特征。本文采用最常见且有效的PCA滤波方法[12]对西北地区各分量残差时间序列的共模误差进行提取。假设时间序列规则且连续，测站数为，观测历元数为，则构成矩阵

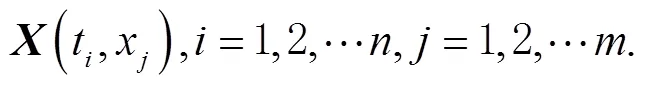
则的协方差阵为

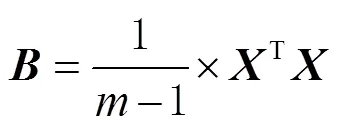
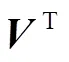
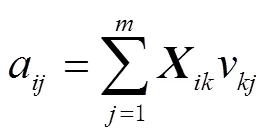
式中：为数据矩阵中的第行第个主成分；表示第个特征向量的第个分量。所得到的主分量按从大到小依次排列，对主分量中有超过一半的对应归一化响应的值按照大于25%这一标准来提取残差时间坐标序列中的共模误差，其中N、E、U3个分量上分别提取的共模误差如图3所示。

表1为剔除共模误差前后残差时间序列的均方根（root mean square，RMS）变化。由表1可知：采用PCA方法时，剔除共模误差前，N、E、U 3个分量的残差坐标时间序列的RMS均值分别为1.871、1.889、7.095 mm；剔除共模误差后，N、E、U3个分量的残差坐标时间序列的RMS均值分别为1.222、1.364、4.210 mm。经PCA滤波后，N方向上平均降低了34.7%；E方向上平均降低了27.8%；U方向上平均降低了40.7%。表明PCA滤波能够很好地提取残差时序中的共模误差，从而提高了GPS站的坐标精度，得到了更为干净的坐标时间序列。

表1 滤波前后RMS均值 mm

3 GPS噪声特征分析

3.1 贝叶斯信息准则数值分析法

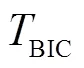
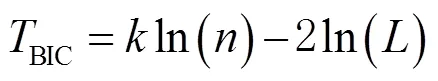
式中：为似然函数；为观测数量；为模型参数的个数。

3.2 滤波前后最优噪声模型建立

许多学者在噪声分析时所选取的模型基本均为白噪声（white noise, WN）+闪烁噪声（flicker noise，FN）、WN/随机游走噪声（random walk noise，RWN）+FN、WN+一阶高斯马尔可夫噪声（generalized Gauss Markov noise，GGM）等[16-17]。根据不同区域上具有不同噪声特性及有色噪声的确定性，假设坐标时间序列中除白噪声（WN）外，还包含闪烁噪声（FN）、随机游走噪声（RWN）、一阶自回归噪声模型（first-order autogressive noise，AR1）、一阶高斯马尔可夫噪声（GGM）、幂律噪声（power-law noise，PL）、马特恩（Matérn，MT）模型[14]、年变化（varying annual，VA）[15]等有色噪声，选取WN+FN、WN+AR1、WN+FN+RWN、WN+FN+VA、WN+GGM、WN+MT、WN+MT+FN、WN+MT+RWN、WN+PL 等9种组合噪声模型来分析噪声分布特性，其结果如图4所示。由图4可知：在PCA滤波前，N方向上最优噪声模型占比最大的为WN+FN组合模型（62.9%），其次为WN+MT组合模型（28.6%）；E方向上最优噪声模型占比最大的为WN+FN组合模型（40%），其次为WN+GGM组合模型（18.6%）和WN+MT组合模型（17.1%）；U方向上最优噪声模型占比最大的为WN+FN组合模型（67.1%），其次为WN+MT组合模型（14.3%）。

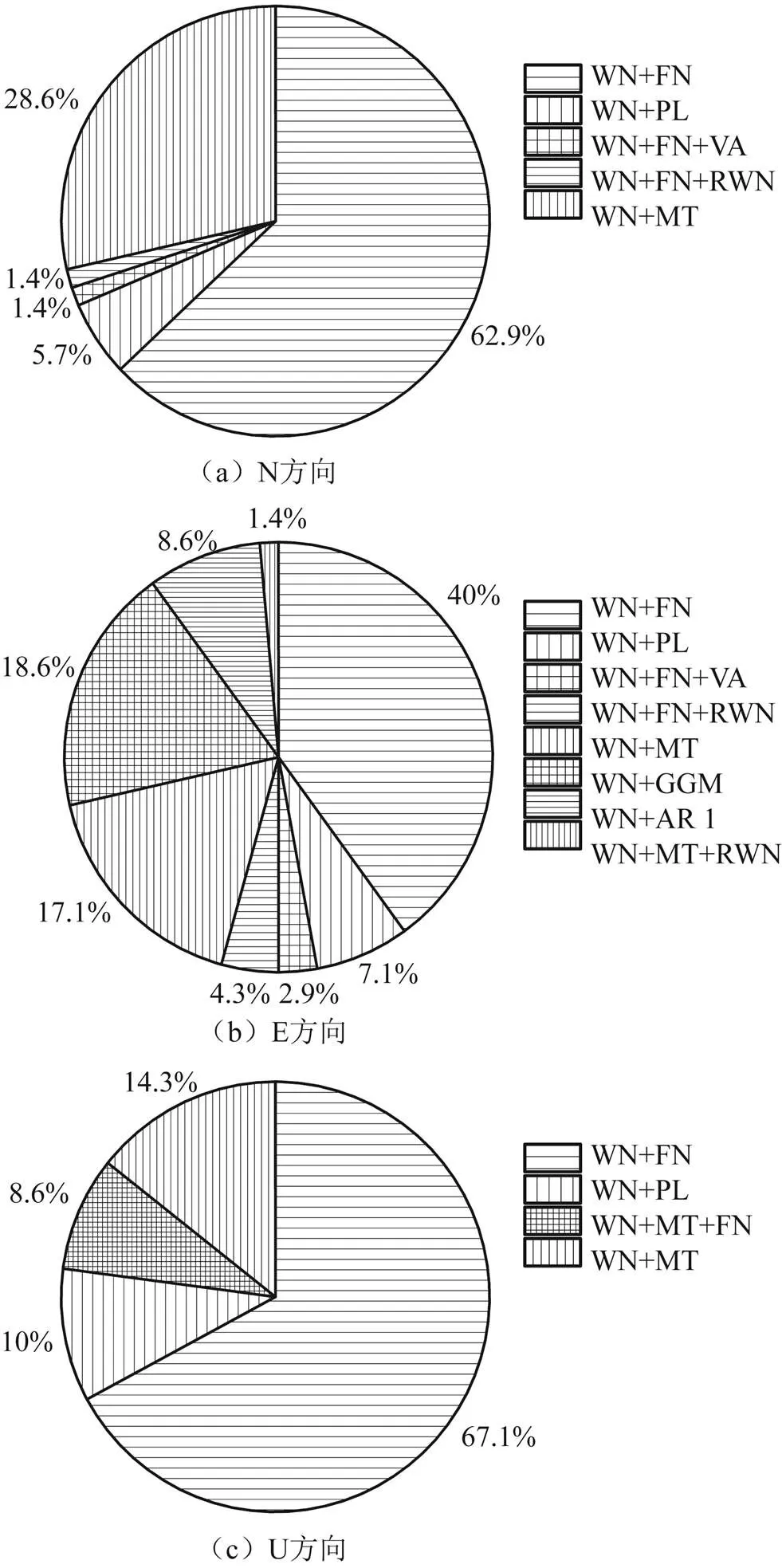
图4 滤波前各分量噪声模型占比

滤波后的噪声模型占比如图5所示。由图5可知，在N、E、U3个不同分量上噪声模型的占比随之改变。在N方向上噪声模型呈多样性，最优噪声模型占比最大的为WN+FN组合模型（35.7%），其次为WN+AR1组合模型（31.4%）；E方向上，WN+FN组合模型与WN+AR1组合模型所占比例均为34.3%，占比最大，其次为WN+PL组合模型（24.3%）；U方向上最优噪声模型占比最大的为WN+FN（71.4%），其次为WN+PL组合模型（12.9%）。

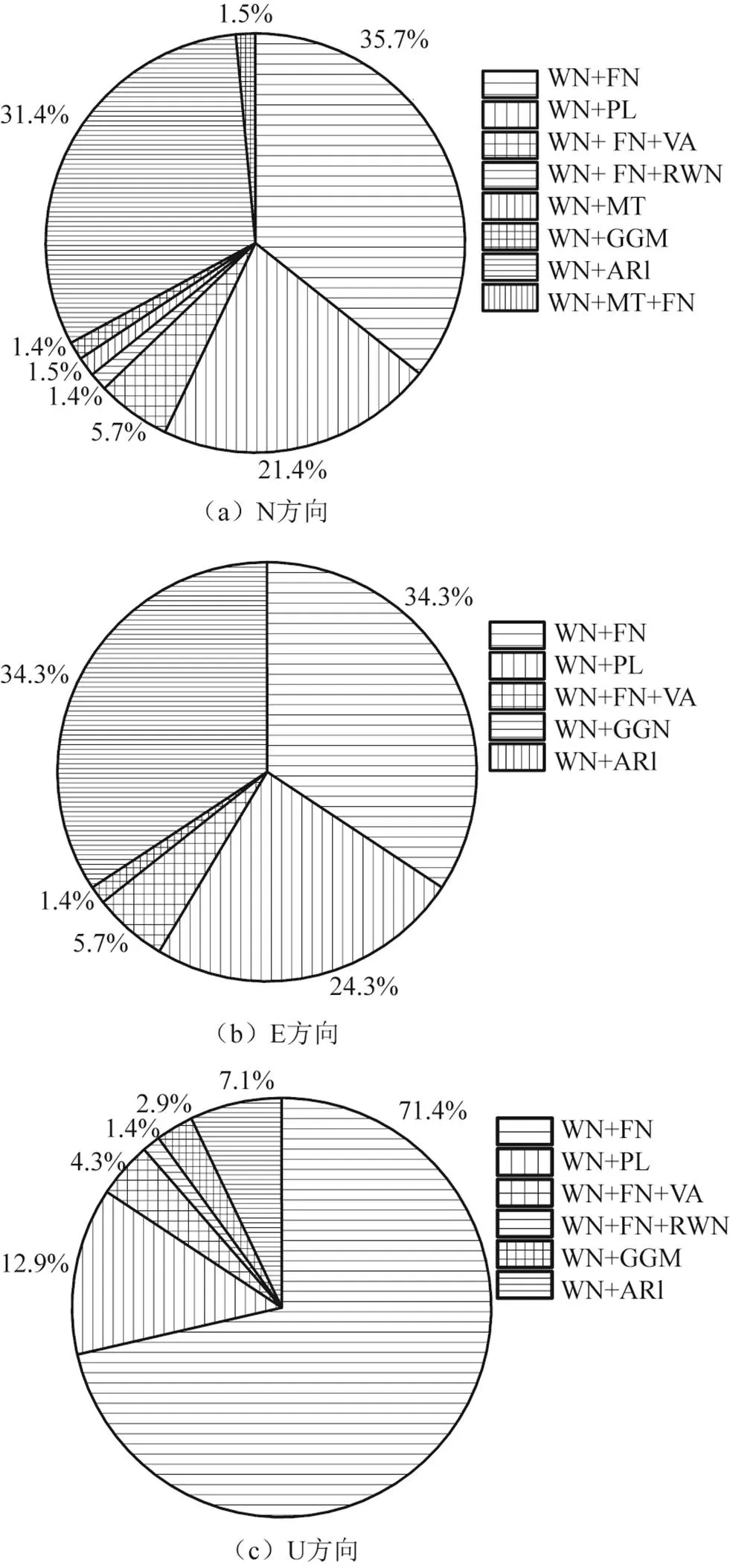
图5 滤波后各分量噪声模型占比

通过对比PCA滤波前后坐标时间序列的最优噪声模型可知，共模误差会影响坐标时间序列最优噪声模型的分布特征，而PCA滤波会大幅降低坐标时间序列的白噪声和闪烁噪声，尤其是N、E方向，表明共模误差具有白噪声和闪烁噪声的特性。滤波前西北地区70个连续站N、E、U3个分量上的最优噪声模型为WN+FN组合模型，其次占比最大的噪声模型为WN+MT；滤波后N、E2个分量上WN+AR1、WN+PL组合模型占比明显增多，WN+FN、WN+MT组合模型占比则显著减少，表明在滤波后部分连续站最优噪声模型发生了改变。共模误差剔除前西北地区70个测站210个分量上最优噪声模型以WN+FN为主，剔除共模误差后最优噪声模型仍以WN+FN为主PCA滤波后虽然最优噪声模型未发生改变，但很有效地降低了白噪声与闪烁噪声的量级，所以在对GPS坐标时间序列进行噪声特性分析时，共模误差的剔除具有必要性。

3.3 滤波前后速度场变化

根据以上研究所得，在顾及有色噪声的影响下，对比分析了滤波前后N、E、U3个分量在国际地球参考框架（international terrestrial reference frame, ITRF）2014下的速度及其不确定度，并绘制滤波前后经最优噪声模型改正后的水平方向和垂直方向上的运动速度场，其结果如图6、图7、表2～表5所示。

图6 滤波前后水平速度场

表2 滤波前水平速度及不确定度 mm/a

表3 滤波后水平速度及不确定度 mm/a

由表2可知：在PCA滤波前，E方向最大速率值为48.948 mm/a，最小速率值为24.626 mm/a；N方向最大速率值为22.257 mm/a，最小速率值为-9.814 mm/a。经70个连续站的统计表明，E方向上标准差为4.701 mm，N方向上标准差为2.374 mm。

由表3可知：滤波后E方向最大速率值为48.936 mm/a，最小速率值为24.024 mm/a；N方向最大速率值为22.177 mm/a，最小速率值为 -10.183 mm/a。滤波后E方向上标准差为4.660 mm，N方向上标准差为1.629 mm，滤波后西北地区连续站水平速度场整体精度较高，其速度不确定度在N、E方向上分别平均降低了38.97%、36.36%。

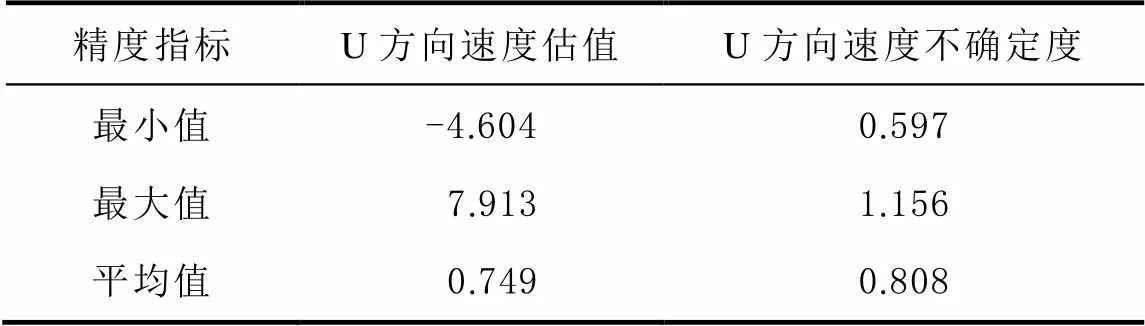
表4 滤波前垂向速度及不确定度 mm/a

表5 滤波后垂向速度及不确定度 mm/a

表4、表5统计结果表明：在垂直方向上，滤波前U方向速率最大值为7.913 mm/a，最小速率值为-4.604 mm/a，统计其标准差为8.133 mm；滤波后速率最大值为6.767 mm/a，最小速率值为-2.130 mm/a，其标准差为8.067 mm。U方向上不确定度平均改善了48.14%。通过PCA滤波剔除共模误差后，发现垂向速度不确定度明显有大幅减小，说明垂向提取的共模误差量级要大于水平方向。剔除共模误差后西北地区连续站水平速度场及垂向速度场精度均高于滤波前水平速度场和垂向速度场，因此在分析坐标时间序列数据及速度场的解算过程时，剔除坐标时间序列中的共模误差是十分必要的。

4 结束语

本文选取了西北地区70个陆态网络连续站10 a的坐标时间序列数据，利用主成分分析法提取了坐标时间序列各分量共模误差，并采用贝叶斯信息准则分析研究了滤波前后西北地区最优噪声模型及速度场变化，最终得出以下结论：

1）利用PCA剔除残差时间序列中的共模误差，结果表明滤波后残差时间序列的平均RMS值在N、E、U 3个分量上分别降低了34.7%、27.8%，40.7%，说明PCA滤波能够很好地提取共模误差，进而提高GPS站的坐标精度。

2）采用贝叶斯信息准则获取滤波前后坐标时间序列的最优噪声模型，结果表明滤波前后西北地区噪声模型存在多样性，整体最优噪声模型仍以WN+FN组合模型为主，但滤波后部分测站最优噪声模型发生改变，说明共模误差的剔除可以有效降低白噪声与闪烁噪声的参数估值，尤其在N、E方向上最为明显。

3）在顾及最优噪声模型的情况下，对比分析滤波前后西北地区速度场变化，结果显示滤波后水平速度场及垂向速度场精度均高于滤波前，N、E、U各分量速度不确定度在滤波后分别平均减少了38.97%、36.36%、48.14%，表明在分析坐标时间序列数据及速度场解算过程时，共模误差的剔除是非常有必要的。

研究结果可为西北地区高精度坐标框架的研究以及地壳运动规律等研究提供参考。

[1] NIKOLAIDIS R. Observation of geodetic and seismic deformation with the global positioning system[EB/OL]. [2022-02-18]. http: //sopac. ucsd. edu/input/processing/pubs/nikoThesis. pdf.

[2] 姚宜斌, 施闯. IGS测站的非线性变化研究[J]. 武汉大学学报(信息科学版), 2007, 32(5): 423-426.

[3] WDOWINSKI S, BOCK Y, ZHANG J, et al. Southern California permanent GPS geodetic array: spatial filtering of daily positions for estimating coseismic and postseismic displacements induced by the 1992 landers earthquake[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B8): 18057-18070.

[4] 陶庭叶, 何蓉, 丁鑫, 等. 安徽省CORS坐标时间序列共模误差与噪声分析[J]. 测绘科学, 2022, 47(1): 49-58, 65.

[5] 占伟, 李经纬. 云南GNSS时间序列共模分量提取分析[J]. 地震研究, 2021, 44(1): 56-63.

[6] 王朝阳, 邢喆, 张峰, 等. 顾及共模误差的西南极GPS坐标时间序列噪声分析[J]. 大地测量与地球动力学, 2022, 42(2): 132-138.

[7] 段举举, 沈云中. 基于方差分量估计的GPS/GLONASS组合点定位[J]. 测绘通报, 2011(4): 4-6.

[8] 张广汉, 余学祥, 严超, 等. 合理权比对GPS/BDS伪距单点定位结果的影响分析[J]. 全球定位系统, 2017, 42(3): 48-53.

[9] 蒋欠欠, 郭英, 于杰. BDS/GPS组合系统在不同随机模型下的精度分析[J]. 海洋测绘, 2019, 39(1): 70-74.

[10] SHUMWAY R H, STOFFER D S. An apprpach to time series smoothing and forecasting using the EM algorithm[J]. Journal of Time Series Analysis, 1982, 3(4): 253-264.

[11] 王健, 许安安, 周伯烨. 顾及共模误差的大区域GPS网坐标时间序列噪声分析[J]. 测绘通报, 2018(4): 6-9, 56.

[12] 殷海涛, 甘卫军, 熊永良, 等. PCA空间滤波在高频GPS定位中的应用研究[J]. 武汉大学学报(信息科学版), 2011, 36(7): 825-829.

[13] BOS M S, FERNANDES R M S, WILLIAMS S D P, et al. Fast error analysis of continuous GNSS observations with missing data[J]. Journal of Geodesy, 2013, 87(4): 351-360.

[14] 成诚, 穆慧敏, 平旗, 等. 山西省GNSS基准站时间序列噪声特征分析[J]. 山西地震, 2021(4): 38-42, 53.

[15] 任安康, 徐克科, 邵振华. GEONET网络GPS坐标时间序列噪声模型建立与分析[J]. 导航定位学报, 2022, 10(2): 141-151.

[16] LILLY J M, SYKULSKI A M, EARLY J J, et al. Fractional Brownian motion, the Matérn process, and stochastic modeling of turbulent dispersion[J]. Nonlinear Processes in Geophysics, 2017, 24(3): 481-514.

[17] KLOS A, BOS M S, FERNANDES R, et al. Noise-dependent adaption of the Wiener filter for the GPS position time series[J]. Mathematical Geosciences, 2019, 51(1): 53-73.

Noise analysis of GPS observation data in land-based network considering common-mode errors

ZHANG Pei, WEI Guangjun, LEI Chuanjin, GAO Maoning

（Faculty of Geomatics, Lanzhou Jiaotong University/National-Local Joint Engineering Research Center of Technologies and Applications for National Geographic State Monitoring/Gansu Provincial Engineering Laboratory for National Geographic State Monitoring, Lanzhou, Gansu 730070, China）

In order to further study on the influence of the extraction of common-mode errors on the analysis of the optimal noise model and velocity field of global positioning system (GPS) coordinate time series, the paper proposed a noise analysis method of GPS observation data in land-based network considering common-mode errors: taking the GPS observation data of 70 land-based network continuous stations during 10 years in Northwest China as the research object, the common-mode error in the residual coordinate time series was eliminated by principal component analysis method; and the changes of optimal noise model and velocity field of the coordinate time series before and after filtering were comparatively analyzed according to the numerical analysis method of Bayesian information criterion. Results showed that the overall optimal noise model in Northwest China before filtering would be mainly based on the white noise (WN) + flicker noise (FN) combination model, and the optimal noise model after filtering would be still based on WN+FN, while the optimal noise model of some sites could have changed after filtering; moreover, the speed uncertainty of each component of N, E and U after filtering could be reduced by an average of 38.97%, 36.36% and 48.14%, respectively, and the accuracy of horizontal velocity field and vertical velocity field would be both higher than that before filtering; in general, the principal component analysis could effectively reduce the levels of white noise and colored noise by excluding common mode errors.

common-mode error; coordinate time series; principal component analysis; Bayesian information criterion; noise model

P228

A

2095-4999(2023)02-0159-07

张沛, 魏冠军, 雷传金, 等. 顾及共模误差的陆态网络GPS观测数据噪声分析[J]. 导航定位学报, 2023, 11(2): 159-165.（ZHANG Pei, WEI Guangjun, LEI Chuanjin, et al. Noise analysis of GPS observation data in land-based network considering common-mode errors[J]. Journal of Navigation and Positioning, 2023, 11(2): 159-165.）DOI:10.16547/j.cnki.10-1096.20230219.

2022-05-12

国家自然科学基金项目（41964008）；兰州交通大学优秀平台项目（201806）。

张沛（1996—），男，甘肃平凉人，硕士研究生，研究方向为GNSS数据处理及理论。

魏冠军（1976—），男，甘肃平凉人，博士，教授，研究方向为变形监测与测量数据处理。