一种顾及测距误差的GNSS四系统加权选星算法

牛 月，李克昭,

一种顾及测距误差的GNSS四系统加权选星算法

牛 月1，李克昭1,2

（1. 河南理工大学 测绘与国土信息工程学院, 河南 焦作 454000；2. 北斗导航应用技术协同创作中心，郑州 450052）

针对全球卫星导航系统（GNSS）四系统可见星测距误差不等，传统公式计算的几何精度因子（GDOP）值不能准确表示多系统组合选星精度和效率等问题，提出一种基于用户等效距离误差（UERE）的GDOP加权选星方法：对不同系统的UERE进行分析，构建一种顾及多种误差的UERE计算模型；并根据谢尔曼-莫里森（Sherman-Morrison）公式增选可见星，通过基于UERE的加权优化法提高计算效率。实验结果表明，相比传统的选星算法，改进的选星算法计算耗时均值可降低72.34%，能够提高多系统快速选星的实时性能。

几何精度因子（GDOP）；用户等效距离误差（UERE）；加权；选星算法；全球卫星导航系统（GNSS）；谢尔曼-莫里森公式（Sherman-Morrison）

0 引言

经过50多年的发展，全球定位系统已经形成以全球定位系统（global positioning system，GPS）、格洛纳斯卫星导航系统（global navigation satellite system，GLONASS）、北斗卫星导航系统（BeiDou navigation satellite system，BDS）和伽利略卫星导航系统（Galileo navigation satellite system，Galileo）为代表的多系统共存局面。使用单卫星系统，难以保证其定位精度、覆盖完整性以及定位实时性和安全性[1-4]。为了提高卫星导航的可靠性、稳定性和安全性，需要融合现有的导航星座系统，进行多系统组合导航定位，增加可见卫星数，同时优化几何精度因子，最终得到更佳的导航定位性能[5-8]。

当前，多系统选星算法主要分为2大类：人工智能选星算法和传统选星算法。人工智能选星算法需要海量数据进行学习训练，反而增加了选星初始运算的复杂性，不利于实际应用[9-11]。传统的选星算法有基于矢端的最大多面体体积法、高度角方位角法、最小几何精度因子（geometric dilution of precision，GDOP）值法等。目前工程中应用最广泛的选星方法还是最小GDOP值法。国内外学者对多星座选星的最小GDOP值法进行了大量的研究。文献[12]提出一种新的 BDS/GLONASS双系统快速选星算法。结果表明，该选星算法效果良好，在损失较小精度的同时大幅度提高了选星效率，此算法在顾及定位精度的同时，又提高了实时性。文献[13]通过接收的Galileo和BDS导航信号，利用加权几何精度因子(weighted geometric dilution of precision，WGDOP)进行了仿真验证与分析。结果表明：与单系统相比，组合系统位置精度因子（position dilution of precision，PDOP）值有所改善，3个方向的定位误差均方根（root mean square，RMS）值较单系统的结果有所改善，在一定程度上提高了导航定位精度。文献[14]用实测BDS/GPS/GLONASS数据进行定位解算，得出多模融合定位精度高、可靠性较优的结论。文献[15]基于GPS/Galileo/GLONASS/BDS组合系统提出了一种适用于多系统组合的快速选星算法。该算法相对于传统的选星算法计算量大大减小，但损失了一定的精度。文献[16]基于用户等效距离误差（user equivalent range error，UERE）对精度衰减因子（dilution of precision，DOP）加权进行了深入的研究，并提出了一种新的选星方法。结果表明：该方法可以防止或减少定位误差，减少计算负载，但是难以保证高精度。文献[17]对4种GNSS全球可用性进行了初步评估。研究结果证明：双系统和三系统的结合可以将GDOP的平均值降低到1.0～1.5，四系统比其他组合可以提供更高的性能，在80%以上区域的GDOP值小于1。同时证明了在四系统组合的情况下，可以提高定位精度，但是不同卫星精度不同，会影响最佳星座选择和定位精度评估的可靠性。文献[18]提出了基于谢尔曼-莫里森（Sherman-Morrison）公式的选星数量确定，结果证明选星数量在12颗卫星时，具有较高的稳定性，且精度得到了保障。文献[19]验证了卫星数目对GDOP的影响，结果表明6颗星比4颗星的GDOP值小，全部可见星的GDOP比6颗星的稍好，但差别已不明显。因此 GDOP 的递减幅度随卫星数目增加而变小，当卫星数目超过6颗以后GDOP递减很小。

在由同质星座构成的导航系统中，计算GDOP值时，通常假定所有卫星的伪距误差是独立的，均值为零、均方根值相同[20]。实际上，由于不同卫星的精度不同，不同卫星测距误差有明显的差异。现有顾及测距误差的多系统组合研究大多是基于双系统和三系统，而对于四系统组合的研究相对有限。而在进行组合的时视卫星测距误差一致，会影响最佳星座选择和定位精度评估的可靠性。因此，为了更加符合实际应用，获得更优的选星结果，提高定位精度，以GPS、GLONASS、BDS和Galileo作为研究对象，提出一种四系统加权选星的方法。该方法通过计算不同卫星导航系统的UERE，建立加权模型，得到卫星单元级的加权矩阵，即以每一颗参与定位的卫星为单位进行加权，然后根据Sherman-Morrison公式确定增选可见星，通过加权提高多系统选星计算运行效率。

1 GNSS四系统加权选星算法

1.1 基于UERE的加权几何精度因子

GDOP表征了用户和可见卫星之间的空间几何分布与定位精度之间的相应关系[21]。GDOP值较小，定位精度较高；GDOP值较大，定位精度较低。GDOP值的数学表达式为

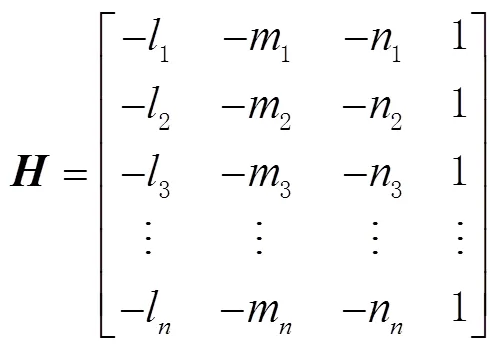
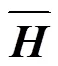
在解算目标的位置时，单系统中常假设所有卫星信号的测距误差相同[22]，但在多系统定位中，则认为伪距测量误差不相同。为了使定位结果更精确，本文用加权最小二乘算法来求解用户位置。加权几何精度因子可以表示为

测量误差越大说明该观测量越不可靠，应该赋予较小的权重。为了改变定位方程组中不同卫星的权重，提高定位精度，此处选取权值的大小反比于对应卫星的伪距误差。

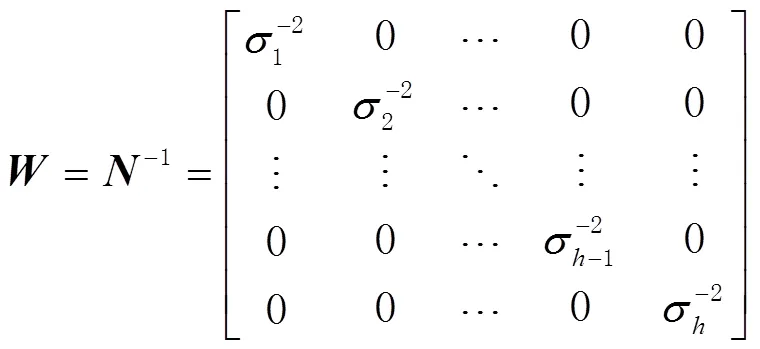
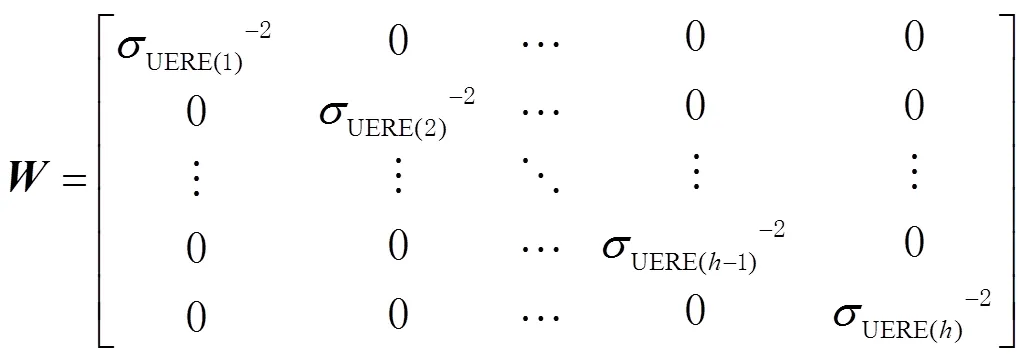
卫星导航系统的定位精度可以用几何精度因子和用户等效距离误差的乘积来表示[23-24]，即

1.2 顾及多种误差的UERE模型

UERE一般被视为是与卫星相关联的各种误差源对伪距测量影响的统计和[25]。本文考虑到电离层延迟误差、对流层延迟误差、多径效应引起的误差、接收机噪声误差以及空间用户的飞行高度不同，建立顾及多种误差的UERE模型表达式如下：

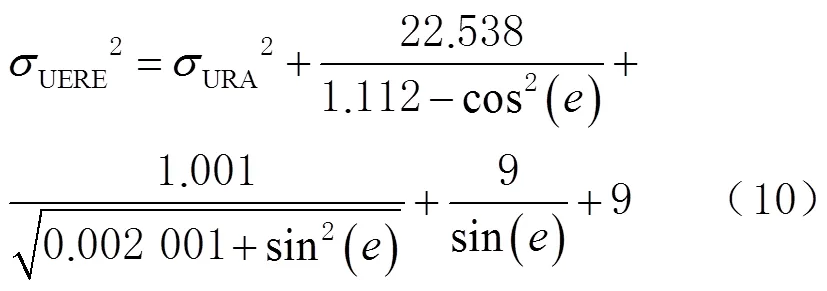
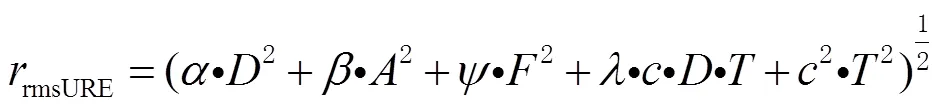
各个系统URE的计算公式如下：

对于BDS的地球静止轨道（geostationary Earth orbit，GEO）、倾斜地球同步轨道（inclined geosynchronous orbits，IGSO）卫星，其计算公式为

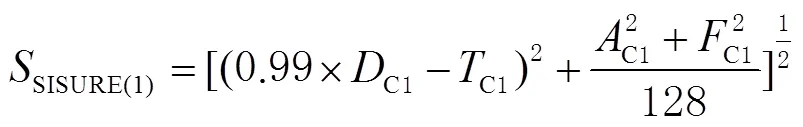
对于BDS的中圆地球轨道（medium Earth orbit，MEO）卫星，其计算公式为

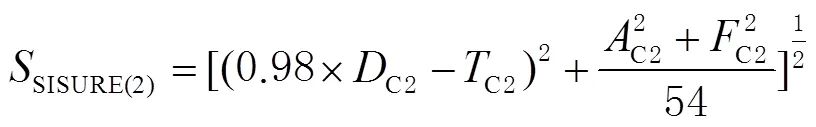
对于GPS，其计算公式为

对于Galileo，计算公式为

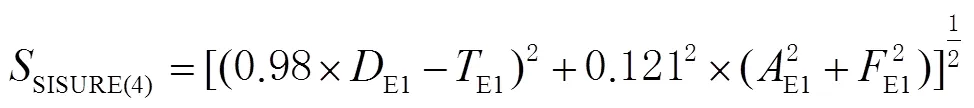
对于GLONASS，其计算公式为

计算可得卫星URA选取参数，如表1所示。

表1 各导航系统卫星的URA选取对照表 m

1.3 基于Sherman-Morrison算法增选可见星

布兰科-德尔加多（Blanco-Delgado）系统论证了可见星与接收机天线相位中心形成的多面体体积最大与GDOP是否最优的关系[27]。得到了多面体体积最大，GDOP较优，仅四面体体积最大与GDOP最优有严格对应关系的结论。因此，可利用四面体体积最大法首先选出4颗可见星。然后，参照文献[18-19]，基于Sherman-Morrison公式增选可见星，其公式如下：

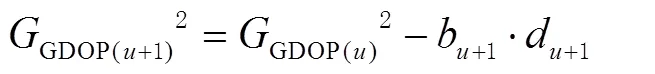
对于加权GDOP选星方法，因为其涉及的未知参数有7个，包括3个待求点的未知坐标参数及4个接收机钟与各自系统的偏差参数，因此，首先不顾及系统加权，增选到6颗星，从第7颗可见星开始加权处理。根据式（17），可得到加权选星所对应的增选可见星公式为

2 实验与结果分析

为进一步验证算法的正确性和有效性，在河南理工大学校园内安置2台华测i90 RTK接收机，采样间隔设为5 s，观测高度设为15°，连续观测24 h，选取6100～31420 s的BDS/GPS/ GLONASS /Galileo四系统数据作为验证数据，通过MATLAB 2019a平台进行数据处理并给出结果分析。

图1给出实验数据对应的BDS、GPS、GLONASS以及Galileo四种系统可见星数目情况。因观测数据量较大，图中横坐标表示观测历元，单位为千秒（ks），下同。

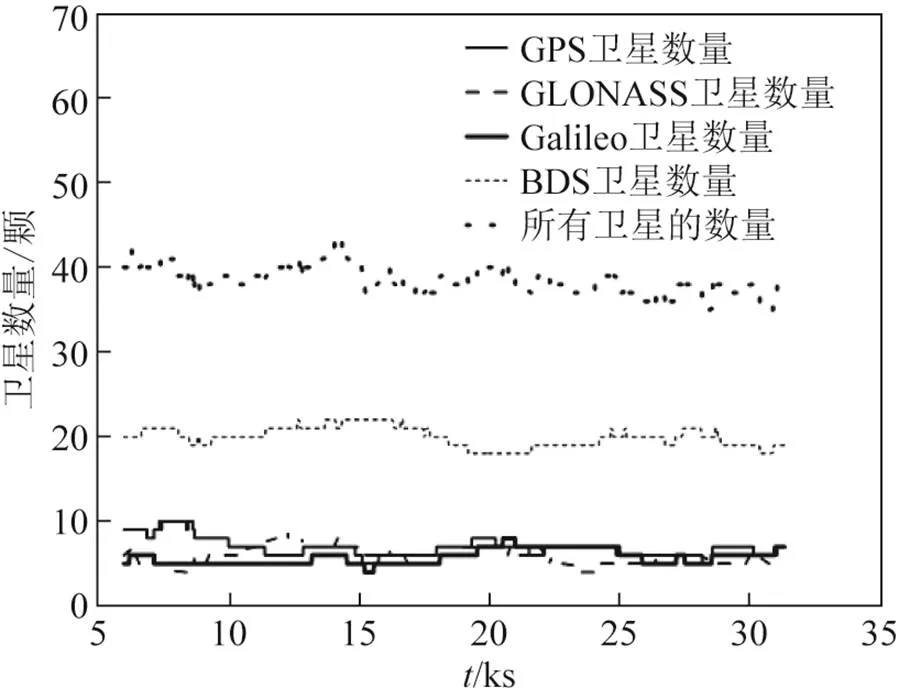
图1 各系统可见星

由图1可以看出，其中GPS最少数量为6颗，BDS最少数量为18颗，GLONASS最少数量为4颗，Galileo最少数量为5颗。当单独使用某一卫星系统时，外界环境容易影响卫星信号的质量。而四个系统接收到总卫星数量在35颗到45颗之间，卫星数目的增加可以改善几何精度因子，进一步可改善导航定位的精度、可靠性和完善性等性能。

考虑到从第7颗星开始采用加权增选星法，因此，图2～图8给出了所有可见星的非加权和加权处理结果，以及增选可见星非加权和加权的处理结果。

图2 7颗星结果

图3 8颗星结果

图4 9颗星结果

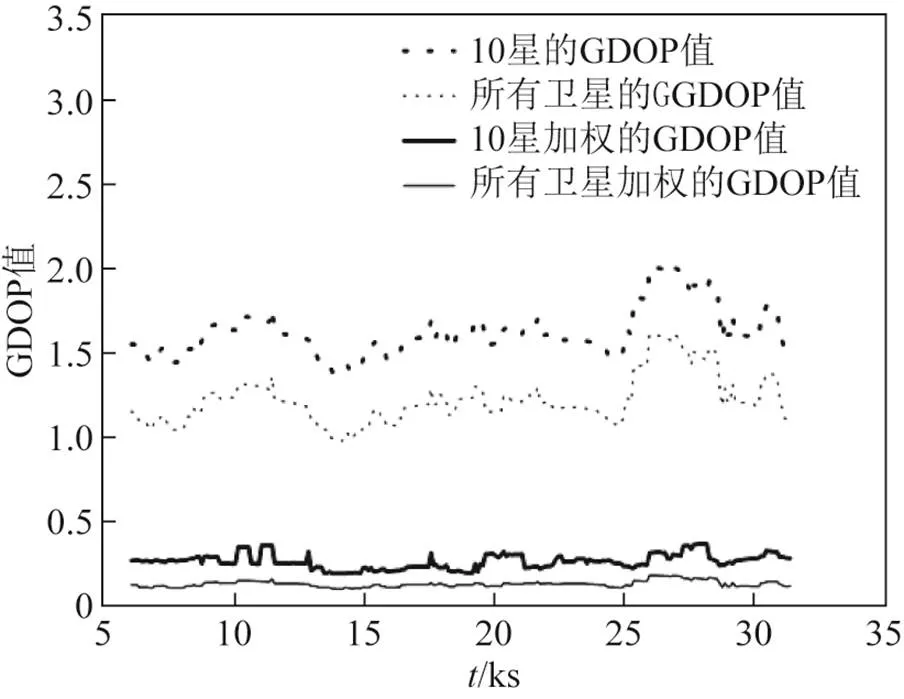
图5 10颗星结果

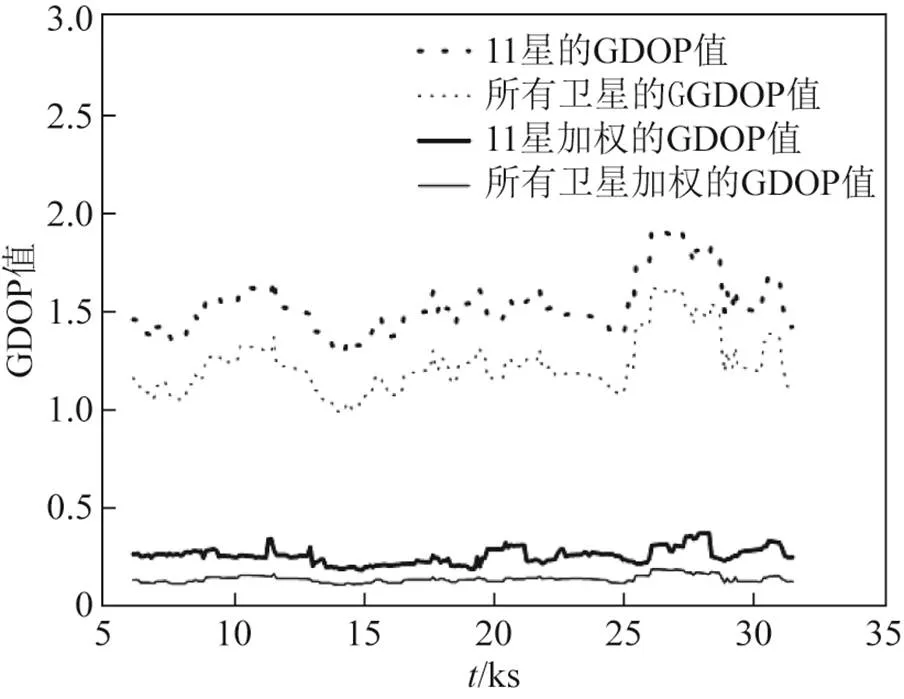
图6 11颗星结果

图7 12颗星结果

图8 13颗星结果

GDOP/WGDOP均值对比结果如表2所示。

表2 GDOP/WGDOP均值对比

由图2～图8和表2可以看出，从整体上来看，随着选星数量的增加，GDOP/WGDOP值逐次减少。非加权方法中：7～9颗星的增加过程中，GDOP 值变化幅度较大，稳定性较差且与所有卫星参与解算得到的GDOP差值较大；从10～11颗星的增加过程中，GDOP值减少趋势较明显，与所有卫星参与解算得到GDOP差值较小；而增加到第12颗星时，GDOP值在逐渐趋于稳定，接近所有卫星参与解算的结果，并且GDOP均小于2，可达到较高的定位精度。加权方法中：在7～8颗星的增加过程中，WGDOP值变化幅度较大；但当增加到第9颗卫星时，WGDOP值趋于稳定，且WGDOP均小于0.3，可达到较高的定位精度。综上所述，当用传统非加权选星法达到12颗星时，GDOP可保持较好的精度和稳定性；当用加权选星法达到9颗星时，WGDOP就有较好的精度和稳定性。另外，图9给出传统非加权选星法12颗星和采用加权优化选星法9颗星时的计算耗时情况。可以看出，当导航定位精度达到较高要求时，本文提出的算法减少了运算时间，提高了四系统选星的计算效率，计算耗时均值提高了72.34%。

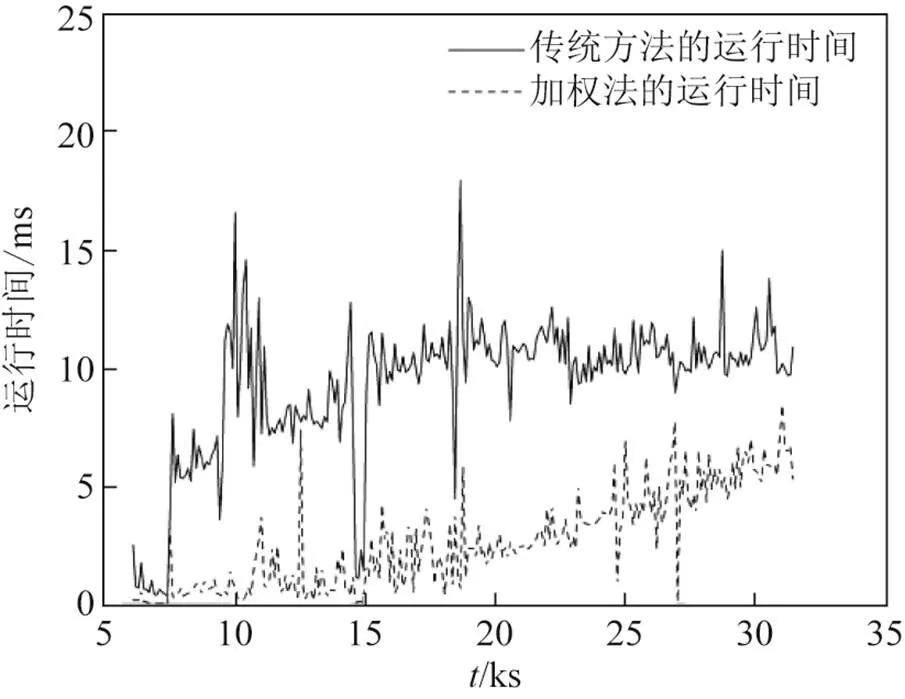
图9 加权法和非加权选星法计算耗时比较

3 结束语

本文提出了顾及多种误差的四系统加权的选星算法，通过实测数据进行了计算验证，得到如下结论：

1）四系统加权GDOP值法相较于传统GDOP值法能够更加准确地反映卫星几何分布与定位精度的关系；

2 根据Sherman-Morrison公式确定选星数量时，在满足较高导航定位精度的情况下，改进的四系统加权选星算法实时性能较优，计算耗时均值降低了72.34%。

[1] 王解先. 全球导航卫星系统GPS/GNSS的回顾与展望[J]. 工程勘察, 2006(3): 55-60.

[2] 张丽. GNSS接收机多系统兼容定位算法研究与实现[D]. 北京: 北京理工大学, 2014.

[3] 曾庆化, 刘建业, 胡倩倩, 等. 北斗系统及GNSS多星座组合导航性能研究[J]. 全球定位系统, 2011, 36(1): 53-57.

[4] ZHANG Q, CHEN Z, YANG C, et al A refined metric for multi-GNSS constellation availability assessment in polar regions[J]. Advances in Space Research, 2020, 66(3): 1-2.

[5] 胡丽乐, 潘林. GPS/GLONASS/BDS/Galileo组合精密单点定位[J]. 导航定位学报, 2017, 5(1): 86-90.

[6] 李征航, 黄劲松. GPS测量与数据处理(第一版)[M]. 武汉: 武汉大学出版社, 2005: 3.

[7] JANUSZEWSKI J. Geometry and visibility of satellite navigation systems in restricted area[J]. Proceedings of the National Technical Meeting of the Institute of Navigation, 2005: 827-839.

[8] TENG Y, WANG J, HUANG Q, et al. New characteristics of weighted GDOP in multi-GNSS positioning[J]. GPS Solutions, 2018, 22(3): 74.

[9] TABATABAEI A, MOSAVI M R. Rapid and precise GLONASS GDOP approximation using neural networks[J]. Wireless Personal Communications, 2014, 77(4): 2675-2685.

[10] JWO D J, LAI C C. Neural network-based GPS GDOP approximation and classification[J]. GPS Solutions, 2007, 11(1): 51-60.

[11] DAN S, EL-SHERIEF H. Navigation satellite selection using neural networks[J]. Neurocomputing, 1995, 7(3): 247-258.

[12] 杨薛涛. BDS/GLONASS双系统组合定位关键技术研究[D]. 西安: 西安电子科技大学, 2018.

[13] 张继海, 袁海波, 等. Galileo_BDS组合卫星导航定位研究[C]//中国卫星导航学术年会. 第八届中国卫星导航学术年会论文集. 北京: 中国卫星导航学术年会组委会, 2017: 38-41[2017-05-23].

[14] 王冰洁, 田申, 钟俞鸿, 等.GNSS多系统融合相对定位选星方案设计及精度分析[J]. 北京测绘, 2021, 35(4): 500-504．

[15] 金玲, 黄智刚, 李锐, 等. 多卫导组合系统的快速选星算法研究[J]. 电子学报, 2009, 37(9): 1931-1936.

[16] SAIRO H, AKOPIAN D, TAKALA J. Weighted dilution of precision as quality measure in satellite positioning[J]. IEEE Proceedings: Radar, Sonar and Navigation, 2003, 150(6): 430-436.

[17] ZHANG Q, CHEN Z, RONG F, et al. Preliminary availability assessment of multi-GNSS: a global scale analysis[J]. IEEE Access, 2019(99): 1.

[18] 石俊鹏. 基于HELMERT多系统加权优化的北斗/GNSS选星算法研究[D]. 焦作: 河南理工大学, 2020. DOI:10.27116/d.cnki.gjzgc.2020.000120.

[19] 丛丽, AHMED I A, 谈展中. 卫星导航几何因子的分析和仿真[J]. 电子学报, 2006(12): 2204-2208.

[20] SAIRO H, SYRJÄRINNE J, et al. Integrity measure for assisted GPS based on weighted dilution of precision[C]// The Institute of Navigation. Proceedings of the 15th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 2002). Portland, OR: The Institute of Navigation, Inc., 2002: 2602-2608[2002-01-01].

[21] WALTER T, BLANCH J, ENGE P. Evaluation of signal in space error bounds to support aviation Integrity[J]. Navigation, 2010, 57(2): 101-113.

[22] 蔡昌盛, 戴吾蛟, 匡翠林, 等. 单频GPS/GLONASS组合单点定位的精度评估[J]. 大地测量与地球动力学, 2011, 31(3): 85-87.

[23] 刘慧娟, 党亚民, 王潜心. 多星座实时导航中一种快速次优的选星方法[J]. 测绘科学, 2013, 38(1): 20-22.

[24] 陈倩, 易炯. 全球4大卫星导航系统浅析[J]. 导航定位学报, 2020, 8(3): 115-120.

[25] BLANCO-DELGADO N, NUNES F D. Satellite selection based on WDOP concept and convex geometry[C]//The Institute of Electrical and Electronic Engineers（IEEE）. Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing: IEEE, 2010: 1-8[2010-12-10].

[26] 李显. 区域混合星座卫星导航系统差分定位与星座间组合导航研究[D]. 长沙: 国防科学技术大学, 2008.

[27] BLANCO-DELGADO N, NUNES F D, SECO-GRANADOS G. On the relation between GDOP and the volume described by the user-to-satellite unit vectors for GNSS positioning[J]. GPS Solutions, 2017, 21(3):1-9.

A GNSS four-system satellite selection method based on UERE weighted optimization

NIU Yue1, LI Kezhao1,2

（1. School of Surveying and Landing Information Engineering, Henan Polytechnic University, Jiaozuo, Henan 454000, China;2. Collaborative Innovation Center of BDS Research Application, Zhengzhou 450052, China）

Aiming at the problems that the visible satellite ranging errors of the four systems of the global navigation satellite system (GNSS) are unequal, and the geometric dilution of precision (GDOP) value calculated by the traditional formula can not accurately represent the precision and efficiency of multi-system combined satellite selection, the paper proposed a weighted satellite selection algorithm for GDOP based on user equivalent range error (UERE): the UERE of different systems was analyzed, and a UERE calculation model considering various errors was constructed; then the visible satellites were added according to Sherman-Morrison formula, and the weighted optimization method based on UERE was used to improve the computational efficiency. Experimental results showed that compared with the traditional satellite selection algorithm, the average calculation time of the proposed satellite selection algorithm would be reduced by 72.34%, indicating that the real-time performance of the multi-system fast satellite selection could be improved.

geometric dilution of precision (GDOP); user equivalent range error (UERE); weighted; satellite selection algorithm; global navigation satellite system (GNSS); Sherman-Morrison formula

P228

A

2095-4999(2023)02-0124-07

牛月, 李克昭. 一种顾及测距误差的GNSS四系统加权选星算法[J]. 导航定位学报, 2023, 11(2): 124-130.（NIU Yue, LI Kezhao. A GNSS four-system satellite selection method based on UERE weighted optimization[J]. Journal of Navigation and Positioning, 2023, 11(2): 124-130.）DOI:10.16547/j.cnki.10-1096.20230214.

2022-04-11

国家自然科学基金项目（41774039）；国家重点实验室项目（6142210200104）。

牛月（1999—），女，河南南阳人，硕士研究生，研究方向为卫星导航与定位技术。

李克昭（1977—），男，甘肃靖远人，博士，教授，研究方向为卫星定位/视觉导航的理论。