多频多GNSS大网发展与解算探讨

李林阳，赖路广，沈 洋，董 行，林家乐

多频多GNSS大网发展与解算探讨

李林阳1,2，赖路广2，沈 洋2，董 行3，林家乐4

（1. 武汉大学 测绘学院，武汉 430072；2. 信息工程大学 地理空间信息学院，郑州 450001；3. 61206部队，北京 100041；4. 61081部队，北京 100089）

为了进一步增强全球卫星导航系统（GNSS）服务的精度、完好性、连续性和可用性，对多频多GNSS大网的解算特点、难点和解算方法进行分析和探讨：归纳多频多全球卫星导航系统（GNSS）大网空间段和地面段的最新进展；然后分析解算的特点与难点，迫切需要统一的解算模型和与之对应的高精度、高效率和智能解算算法；最后从非差模型、并行解算和智能解算3个方面总结解算方法。

全球卫星导航系统（GNSS）；多频多系统；大网解算

0 引言

作为国民经济建设和国防现代化的关键基础设施和宝贵战略资源，全球卫星导航系统（global navigation satellite system，GNSS）大网可以提供高精度时空基准，尤其是2020年7月31日，北斗三号全球卫星导航系统即北斗三号（BeiDou-3 navigation satellite system，BDS-3）正式开通以来，为全球用户提供了优质的综合定位、导航及授时（positioning，navigation and timing，PNT）服务。如图1所示，当前多频多GNSS大网主要由地面大型GNSS基准站网、中高轨GNSS卫星和低轨卫星组成，是我国正在建设的更加泛在、更加融合、更加智能的国家综合PNT体系[1]的核心组成部分，可以建立与维持天地一体的高精度时空基准，满足军用和民用对精准时空基准的需求，应用于地球参考框架建立与维持、气象学研究、地球动力学研究等领域，服务于我国“一带一路”倡议—陆海通道时空基准维持与精化。

图1 多频多GNSS大网组成

在地面段，通过公开渠道可从互联网获取全球范围内的GNSS基准站的观测数据，基准站的数量超过了5000个。据统计，美国内华达州大地测量实验室日常处理的超过17000个地面基准站[2]，若加上尚未公开的国家级、省市级和行业级等基准站，如千寻建成的2400多个基准站，中国移动建成的4400个基准站，全球分布的GNSS基准站数量不少于2万个，甚至可能超过4万个。

图2进一步给出了各个国家和地区拥有的国家级地面基准站的数量。可以看出，中国、美国和日本境内都建成了上千个GNSS基准站。

图2 全球范围内主要的GNSS基准站网分布及其规模

在空间段，GNSS卫星包括全球定位系统（global positioning system，GPS）、格洛纳斯导航卫星系统（global navigation satellite system，GLONASS）、北斗卫星导航系统（BeiDou navigation satellite system, BDS）、伽利略卫星导航系统（Galileo navigation satellite system，Galileo）4个全球系统和其他区域系统，截至2022年3月17日，在轨运行的可用GNSS卫星数量已达132颗，另有13颗处于在轨维护状态。低轨卫星作为天基监测站，可以增强GNSS卫星定轨的精度[3]，尤其对BDS（海外建站较为困难）具有重要意义[4]，搭载GNSS接收机的低轨卫星数量已近百颗。当前，数以百计甚至千计的低轨导航增强卫星群正在加紧部署，如国内鸿雁、虹云和微厘空间等低轨导航增强星座，这些星座将是未来的多频多GNSS大网的重要组成部分[5]。

1 多频多GNSS大网解算特点与难点

1.1 多频多GNSS大网解算特点

多频多GNSS大网解算具有以下3个特点：

1）频率多、观测值类型多、待估参数多。如图3所示，多频是一个重要特征，GPS现代化进程中双频卫星由三频卫星取代，提供L1、L2和L5 3个频点的服务；GLONASS由频分多址逐步过渡到三频码分多址，包括G1、G2和G33个频率；Galileo则提供五频服务，包括E1、E6、E5a、E5b和E5ab；我国北斗卫星导航（区域）系统即北斗二号（BeiDou navigation satellite（regional）system，BDS-2）提供全星座B1I、B2b和B3I三频服务，BDS-3提供B1C、B1I、B3I、B2b、B2a和B2a+b 6个频点的服务；日本准天顶卫星系统（quasi-zenith satellite system，QZSS）提供L1、LEX、L2和L54个频点的服务；印度区域卫星导航系统（navigation with Indian constellation，NavIC）提供S和L52个频点的服务。

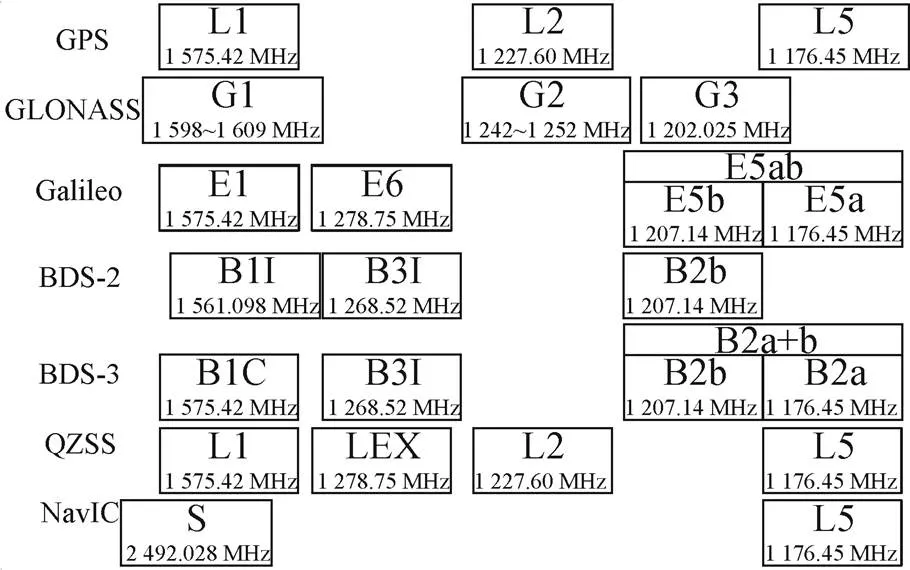
图3 GNSS多频信号分布

观测值类型不仅包括GNSS卫星与GNSS接收机之间的伪距、载波相位和多普勒等单向观测值，而且包括GNSS卫星之间的星间链路、GNSS卫星与地面锚固站的双向测量等，未来即将包括低轨导航增强卫星之间、低轨导航卫星与中高轨GNSS卫星、低轨导航卫星与地面基准站之间的观测值；将文献[6]提出的计算方法扩展至三频，假设500个测站观测到四系统的100颗三频卫星，平均每个测站观测到30颗卫星，单天所有待估参数的总量为361606个，历元活跃的待估参数数量为66106个。在由卫星轨道和接收机坐标、卫星和接收机钟差、对流层和电离层延迟、模糊度和各类偏差等组成的全网待估参数中，模糊度参数的数量最多，通常是其他参数数量的3～4倍（如表1所示）。

表1 500个测站观测到四系统的100颗三频卫星对应的待估参数数量 个

2）待估参数状态复杂。地面基准站为静态模式，高、中、低轨卫星的动力学模型复杂，不同分析中心采用的卫星姿态模型往往不同，尤其是在卫星偏航姿态异常期间；伪距和相位硬件偏差的时变性差异不仅存在不同系统之间（如BDS-2存在星上多径效应），而且同一系统的不同类型卫星间也存在差异（如GPS BLOCK-ⅡF卫星存在显著的频间钟偏差（inter-frequency clock bias，IFCB）），待估参数的状态模型复杂，给数据处理带来极大的挑战，往往会带来模型和参数不符合、不适用和结果非最优等问题。

3）解算过程复杂、耗时长。解算过程涵盖了预处理、轨道积分、观测方程构建与线性化、法方程构建与平差解算、残差编辑、迭代解算、模糊度固定、网平差、精度评价、偏差特性分析等，并且质量控制贯穿于整个数据处理过程。数据处理呈计算密集型和数据密集型特性，随着GNSS网规模的扩大，解算耗时迅速增加。

1.2 多频多GNSS大网解算难点

针对以上3个特点，为提升多频多GNSS大网服务的性能，多频多GNSS大网解算亟须解决以下3个难题：

对于学生综合素质的培养方面，现阶段很多高职院校在课程体系设置过程中过于重视专业课的设置，而相对忽略了与学生综合素质相关的通识课程。对于创新能力的培养方面，高职院校应立足于旅游信息化发展的实际要求，合理设置旅游相关的电子商务、网站创建以及大数据管理等课程内容的设置，大力培养当前旅游行业急需的适应互联网发展的旅游专业人才[2]。

首先，针对特点1，多频多GNSS大网解算的模型需要统一。目前以双频观测值、无电离层组合和双差模型为基础建立的解算模型，消去了部分原始观测信息，导致无法解算部分待估参数，也无法利用待估参数的先验约束提升解算结果的质量，因此这种解算模型已经无法完全满足多频多GNSS背景下高精度GNSS数据处理、服务和多样化应用的需求。更为丰富的观测值类型和更多的频率，需要统一的解算模型作为支撑，以充分发挥多频多GNSS大网多频率、多类型观测值的优势。

其次，针对特点1和特点3，多频多GNSS大网解算的速度需要提高，主要包括：

1）多模GNSS实时轨道确定。国际GNSS服务组织（international GNSS service，IGS）提供的实时轨道是根据超快速实测产品预报的，IGS发布的超快速轨道的更新频率仅为6 h，武汉大学分析中心提高到了1 h；为支持包括BDS、GLONASS和Galileo等星座，卫星的数量将增加3倍或更多，计算量也将按比例增长；基于轨道预报获得的实时轨道易受动力学模型不准、姿态模式切换和轨道机动的影响，基于实时观测数据的实时定轨可以有效克服上述不足，尤其对我国BDS意义重大[7]，但实时定轨的计算速度需要提升。

2）高采样率实时钟差估计（含硬件偏差）。伪距和相位硬件偏差可以与钟差一起进行估计，并配套使用。IGS一般采用50～100个地面站的实时数据流进行滤波解算，采样率一般为5或10 s；若加入更多的地面跟踪站，将进一步提高卫星钟差的精度和可靠性，而高精度实时定位对1 s甚至更高采样率的实时钟差的需求十分强烈，新一代GNSS卫星频率的增加、星间和星地链路观测值的引入等，都会显著增加GNSS大网的计算量。

3）大型地面GNSS基准站网解算。如图4所示，IGS累积周解的大小逐步扩大，目前已接近7GB，GPS 2140周（2021年1月10日至2021年1月16日）协方差矩阵的阶数达到了23376阶。图4中的2次阶跃分别对应IGS的第一次和第二次重处理，例如第二次重处理在GPS 1933周新增了349个跟踪站。在国际地球参考框架（international terrestrial reference frame，ITRF）更新时，IGS采用精化后的误差模型和一致的解算策重新计算自1994年以来的海量观测数据，生成新框架下的周解产品，计算量巨大，例如最新的作为ITRF2020输入的第3次重处理。同样，当前ITRF框架站较为稀疏，当框架站受地震、更换仪器设备等影响不可用时，将给应用带来诸多不便，如受IGS08框架站不可用的影响，不得不重新建立新的框架，因此为了支持全球ITRF的解增加10倍密度，分析中心的计算量将增长到100倍甚至更高的数量级[8]。

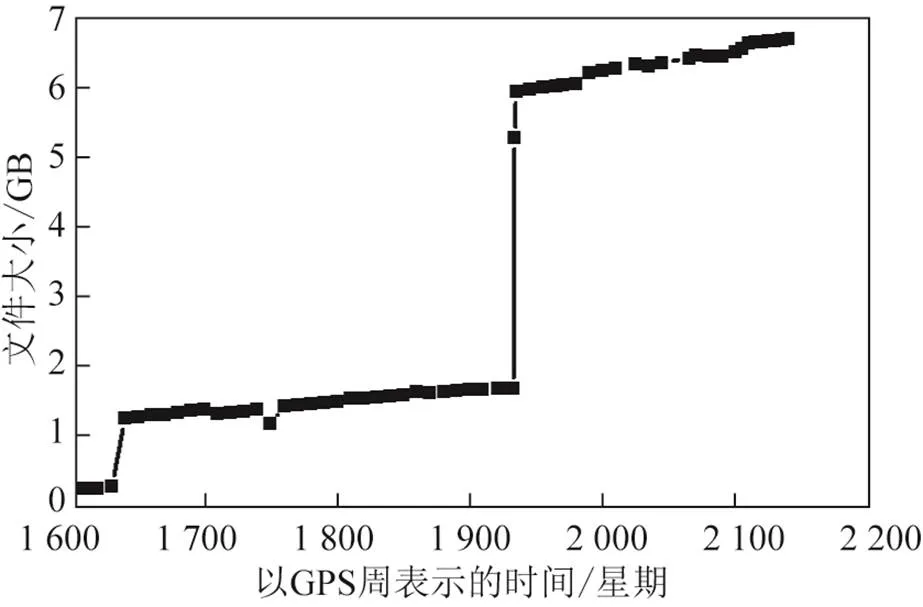
图4 IGS跟踪站累积解文件大小

最后，同时针对特点1至特点3，多频多GNSS大网解算的自适应能力和智能程度亟须提升。GNSS大网解算的精度和速度取决于对星—星、星—地单向或双向观测的认知，状态参数的建模方法，以及摄动因素、轨道机动前后、地影期间偏航姿态和大气异常扰动等的控制、调节与修正，需要根据状态不符值、预测残差、观测残差、闭合差、中误差等，选择模型改正，调节阈值和窗口，对函数模型和随机模型误差进行拟合、修正和补偿，平衡观测信息与动力学模型信息的贡献。针对观测模型异常、动力学模型异常等问题，反复进行检验和诊断，迭代解算，额外增加了计算时间。

2 多频多GNSS大网解算方法

多频多GNSS大网数据处理迫切需要与之对应的高精度和高效率处理模型与方法作为支撑，以充分发挥大网的优势，提升大网计算的精度和时效性[9]。

2.1 非差模式下多频多GNSS大网统一解算模型与方法

在原始观测值层面，不进行任何星间差分、站间差分、历元间差分或者线性组合，基于非差模式建立统一的多频多GNSS数据处理模型，整体估计轨道、钟差、伪距和相位硬件偏差，既能最大限度地利用原始多模多频观测信息，又能同时保证数学严密性，最终提供一套完整的解算产品[10-12]。非差模式能够实现电离层延迟、对流层延迟和硬件偏差在状态域的精准建模[13]，有助于全球高精度电离层模型的构建和实时大气可降水量的反演，并支持全球范围内单台接收机的非差模糊度固定。

针对非差模式下大量的多类型观测值，预处理与质量控制是多频多GNSS大网解算的重要基础和关键环节，同时包括观测异常和动力学模型异常的探测、诊断和调节，并且质量控制贯穿于整个解算过程，其优劣和速度直接关系到多频多GNSS大网解算的精度和时效性[14]。

针对非差模式下规模庞大的待估参数，首先面临的是参数的消秩亏和可估计性问题，构建非差满秩观测方程。采用S-基准变换和消秩亏理论，文献[15]推导了GPS网非差数据处理模型；文献[16]采用满足最小约束解的模型正则化方法，削弱钟差与硬件偏差的相关性；文献[17]重新精选了伪距和相位硬件偏差、模糊度和钟差基准；文献[18]进一步推广到多频多GNSS模式下的基准选择；文献[19-20]系统分析了非差非组合的7种秩亏性，通过附加基准约束建立了非差非组合满秩观测方程。

其次是非差高阶多元观测方程的解算，主要方法包括：

1）组合观测值和模型，降低采样率（采用300 s甚至更长采样间隔），减少观测值和待估参数总量。在卫星钟差估计中：文献[21]联合低采样率非差模型和高采样率历元间差分模型；文献[22]联合差分相位观测方程和非差伪距观测方程，虽然消除了模糊度，降低了计算量，但无法估计相位硬件偏差。

2）消除与恢复参数，降低法方程维度。模糊度参数和对流层参数都是典型的随时间相关的参数，只在特定的时间段内有效，分为活跃和不活跃2种状态。若法方程仅考虑活跃参数，则其维度会大大降低。文献[6]通过消去大量失效的钟差、对流层和模糊度等参数，降低了法方程的维度和内存消耗。但随着GNSS网的扩大，消参的过程将会特别耗时[23]。

3）扣除模糊度，生成载波距进行整网解算。文献[24]采用固定的双差模糊度、文献[23]采用非差小数相位偏差（fractional cycle bias，FCB）、文献[25]采用整数卫星钟差，扣除非差模糊度，得到新的观测值（载波距），联合载波距和伪距进行整网解算。

4）非差滤波实时解算方法。美国喷气推进实验室（Jet Propulsion Laboratory，JPL）、法国国家太空研究中心（Centre National d'Etudes Spatiales，CNES）分别采用卡尔曼滤波和均方根信息滤波实时估计了一套自洽的四系统轨道、钟差、伪距和相位硬件偏差等产品；文献[26]采用分块正交三角分解提高了GNSS大网均方根信息滤波解算中豪斯霍尔德变换（Household）变换的效率；文献[27]基于分块递推最小二乘配置方法，对待估参数松弛、连接以及轨道状态参数转移递推，兼容实时滤波定轨。

5）非差高维模糊度的搜索固定。高维模糊度解算效率往往受格基规约的影响更显著，文献[28]系统分析了降相关对搜索效率的影响，在促使基向量按一定方向排序的基础上，高效快速的整周模糊度搜索固定是关键难题[29]。文献[30]结合基于收缩搜索空间的维泰尔博-比列里（Viterbo-Biglieri，VB）算法和基于震荡式枚举的施诺尔-托伊赫纳（Schnorr-Euchner，SE）算法，提出了SE-VB搜索算法。文献[31]采用分块处理算法从规约的角度提高了高维模糊度解算的整体效率。而当无法固定模糊度全集时，可以优选子集进行部分模糊度固定。

2.2 多频多GNSS大网并行解算方法

多频多GNSS大网解算是易于并行设计的。在解算流程上，大规模GNSS网数据处理还具有一个极其重要的特性：具有许多易于并行计算的过程，如时段间/基线间/站间/系统间/频率间/组合观测值间/星间/历元间操作、观测方程构建、法方程解算、模糊度搜索固定和网平差等。并行化分解计算密集型运算、多节点分布式处理数据密集型解算，可以有效提高GNSS大网解算的效率[32-33]。目前主要包括站间和基线间并行、矩阵运算并行2个方面：

1）粗粒度的站间和基线间并行。2007年发布的伯尔尼（Bernese）5.0软件支持多线程站间并行，意大利、美国和中国基准站解算都采用了站间和基线间并行计算。

2）细粒度的矩阵分块、并行分解和并行求逆。采用多节点多核并行计算技术，已建立的并行特性良好的模型包括均方根信息滤波中乔列斯基（Cholesky）分解法的并行计算[34-35]、参考框架的分布式计算[36]、基线向量网平差[37]、电离层并行解算[38-39]、并行加速方差/协方差更新的实时定轨和钟差并行估计[40]、基于等价理论的GNSS并行解算[41]。

文献[42]对JPL开发的非差解算软件进行了多核并行升级；2020年澳大利亚地球科学局开源的GNSS网解软件采用英特尔数学核心库（Intel math kernel library，MKL）和开源基本线性代数子程序（open-source basic linear algebra subprograms, OpenBLAS）进行多核并行解算。

2.3 多频多GNSS大网智能解算方法

针对多频多GNSS大网众多的观测值类型和复杂的状态模型：文献[43]提出了探测、诊断和调节（detection identification adaptation，DIA）方法；文献[44]创建/构造了一套基于/融合自适应因子、自适应滤波、方差分量估计的自适应抗差滤波理论体系，建立了自适应定轨理论，通过对参数和模型的自适应精准调节，可以降低检验、诊断和调整的次数，减少迭代解算，从而在一定程度上提高解算速度；针对BDS轨道机动、地影和零偏期间定轨，文献[45]提出采用自适应均方根信息滤波定轨和过程噪声自适应调节方法；文献[46-47]进一步研究了GNSS非模型化误差的性质，提出了一套假设检验理论、观测值定权和函数模型补偿方法。

机器学习算法智能、快速和高效，逐步应用到GNSS领域。文献[48]采用长短时记忆网络（long-short term memory，LSTM）对电离层进行建模预测；为提升GNSS实时动态定位性能，文献[49]构建了多层递归神经网络（recurrent neural network, RNN）；文献[50]采用LSTM与抗差卡尔曼（Kalman）滤波组合，提高了伪距单点定位精度。文献[51]采用均值聚类算法、高斯混合聚类和模糊-均值3种非监督学习聚类方法，分离了城市复杂环境中的视线信号、多路径和非视线信号。

3 结束语

本文首先概述了多频多GNSS大网空间段和地面段的最新进展；其次分析了多频多GNSS大网解算的特点与难点；最后从非差模型、并行解算和智能解算3个方面，总结了多频多GNSS大网解算方法。

未来低轨导航增强卫星作为导航系统的新型力量，可以与已经部署的中高轨GNSS星座形成优势互补，将极大拓展与完善我国下一代BDS，进一步增强GNSS服务的精度、完好性、连续性和可用性。其解算特点、难点和解算方法值得进一步分析和挖掘。

在并行解算方面，目前多采用多节点与多核中央处理器（central processing unit，CPU）并行相结合的方式，还未涉及加速性能更突出的众核图形处理器（graphics processing unit，GPU）；在算法层面，需要进一步结合站间、系统间、频率间、观测值间、星间、历元间等操作和预处理、观测方程构建与解算、模糊度搜索固定等解算流程，进一步挖掘细粒度的并行策略，建立性能优越的并行解算模型。未来的低轨导航卫星实时定轨和钟差估计，也亟需高效率的并行处理算法。

在智能解算方面，针对多模GNSS大网解算的复杂性，需要进一步对解算任务进行特征量化，构建智能机器学习模型，提升自适应能力和智能化程度。

[1] 杨元喜. 综合PNT体系及其关键技术[J]. 测绘学报, 2016, 45(5): 505-510.

[2] BLEWITT G, HAMMOND W C, KREEMER C. Harnessing the GPS data explosion for interdisciplinary science [EB/OL]. (2018-09-24) [2022-06-18]. https://doi.org/10.1029/2018EO104623.

[3] Zhu S X, Reigber C, König R. Integrated adjustment of CHAMP, GRACE, and GPS data[J]. Journal of Geodesy, 2004, 78(1/2): 103-108.

[4] Zhao Q L, Wang C, Guo J, et al. Enhanced orbit determination for BeiDou satellites with FengYun-3C onboard GNSS data[J]. GPS Solutions, 2017, 21(3): 1179-1190.

[5] 张小红, 马福建. 低轨导航增强GNSS发展综述[J]. 测绘学报, 2019, 48(9): 1073-1087.

[6] Ge M R, Gendt G, Dick G, et al. A new data processing strategy for huge GNSS global networks[J]. Journal of Geodesy, 2006, 80(4): 199-203.

[7] Dai X L, Lou Y D, Dai Z Q, et al. Real-time precise orbit determination for BDS satellites using the square root information filter[J]. GPS Solutions, 2019, 23(2): 45.

[8] Boomkamp H. Global GPS reference frame solutions of unlimited size[J]. Advances in Space Research, 2010, 46(2): 136-143.

[9] 李林阳, 张学东, 黄娴, 等. 大规模GNSS网发展及数据处理现状[J]. 测绘通报, 2018(10): 1-5.

[10] Schönemann E, Becker M, Springer T. A new approach for GNSS analysis in a multi-GNSS and multi-signal environment[J]. Journal of Geodetic Science, 2011, 1(3): 204-214.

[11] Montenbruck O, Hauschild A, Steigenberger P. Differential code bias estimation using multi-GNSS observations and global ionosphere maps[J]. Navigation, 2014, 61(3): 191-201.

[12] 张小红, 胡家欢, 任晓东. PPP/PPP-RTK新进展与北斗/GNSS PPP定位性能比较[J]. 测绘学报, 2020, 49(9): 1084-1100.

[13] Wübbena G, Schmitz M, Bagge A. PPP-RTK: precise point positioning using state-space representation in RTK networks[C]//The Institute of Navigation. Proceedings of the 18nd International Technical Meeting of The Satellite Division of the Institute of Navigation(ION GNSS 2005). Long Beach, California: The Institute of Navigation, Inc., 2005: 2584-2594[2022-06-28].

[14] 蔡华. GNSS大网实时数据快速解算方法应用研究[D]. 武汉: 武汉大学, 2010．

[15] JONGE P J D. A processing strategy for the application of the GPS in networks[M]. Amsterdam: NCG Nederlandse Commissie voor Geodesie, 1998: 37-59.

[16] 辜声峰. 多频GNSS非差非组合精密数据处理理论及其应用[D]. 武汉: 武汉大学, 2013.

[17] 张宝成, 欧吉坤, 袁运斌. 基于精选基准消秩亏的GNSS参考网数据处理方法[J]. 测绘学报, 2014, 43(9): 895-901.

[18] Odijk D, Zhang B C, Khodabandeh A, et al. On the estimability of parameters in undifferenced, uncombined GNSS network and PPP-RTK user models by means of S-system theory[J]. Journal of Geodesy, 2016, 90(1): 15-44.

[19] 范磊. 北斗/GNSS实时高效精密定轨及频间时钟偏差特性研究[D]. 武汉: 武汉大学, 2017.

[20] Strasser S, Mayer-Gürr T, Zehentner N. Processing of GNSS constellations and ground station networks using the raw observation approach[J]. Journal of Geodesy, 2019, 93(7): 1045-1057.

[21] Bock H, Dach R, Yoon Y, et al. GPS clock correction estimation for near real-time orbit determination applications[J]. Aerospace Science and Technology, 2009, 13(7): 415-422.

[22] Ge M R, Chen J P, Dousa J, et al. A computationally efficient approach for estimating high-rate satellite clock corrections in realtime[J]. GPS Solutions, 2012, 16(1): 9-17.

[23] Chen H, Jiang W P, Ge M R, et al. An enhanced strategy for GNSS data processing of massive networks[J]. Journal of Geodesy, 2014, 88(9): 857-867.

[24] Blewitt G. Fixed point theorems of GPS carrier phase ambiguity resolution and their application to massive network processing: Ambizap[J]. Journal of Geophysical Research, 2008, 113(B12): B12410.

[25] 阮仁桂, 魏子卿, 贾小林. 一种基于星间单差模糊度固定的载波伪距生成方法[J]. 测绘学报, 2018, 47(12): 1591-1598.

[26] Gong X P, Gu S F, Lou Y D, et al. An efficient solution of real-time data processing for multi-GNSS network[J]. Journal of Geodesy, 2018, 92(5): 797-809.

[27] 赵齐乐, 徐小龙, 马宏阳, 等. GNSS实时精密轨道快速计算方法及服务[J]. 武汉大学学报·信息科学版, 2018, 43(12): 2157-2166.

[28] 卢立果, 刘万科, 李江卫. 降相关对模糊度解算中搜索效率的影响分析[J]. 测绘学报, 2015, 44(5): 481-487.

[29] Li Z N, Li M, Shi C, et al. Impact of ambiguity resolution with sequential constraints on real-time precise GPS satellite orbit determination[J]. GPS Solutions, 2019, 23(3): 85.

[30] Chang X W, Yang X, Zhou T. MLAMBDA: a modified LAMBDA method for integer least-squares estimation[J]. Journal of Geodesy, 2005, 79(9): 552-565.

[31] 刘万科, 卢立果, 单弘煜. 一种快速解算高维模糊度的LLL分块处理算法[J]. 测绘学报, 2016, 45(2): 147-156.

[32] Li L Y, Lu Z P, Chen Z S, et al. Parallel computation of regional CORS network corrections based on ionospheric-free PPP[J]. GPS Solutions, 2019, 23(3): 70.

[33] 李林阳. 大规模全球GNSS网云计算方法与应用[J]. 测绘学报, 2020, 49(6): 804.

[34] Baboulin M, Giraud L, Gratton S, et al. Parallel tools for solving incremental dense least squares problems: application to space geodesy[J]. Journal of Algorithms & Computational Technology, 2006, 3(1): 117-133.

[35] 杨凯. 基于OPENMP的高性能GNSS法方程解算方法研究[J]. 大地测量学与地球动力学, 2013, 33(1): 141-144.

[36] Boomkamp H. Global GPS reference frame solutions of unlimited size[J]. Advances in Space Research, 2010, 46(2): 136-143.

[37] 崔阳, 吕志平, 张友阳, 等. 大型高精度GNSS基线向量网并行抗差估计[J]. 测绘学报, 2015, 44(5): 495-502.

[38] 施闯, 王成, 张涛. 基于超算的全球电离层模型快速并行解算[J]. 武汉大学学报(信息科学版), 2018, 43(12): 2093-2098.

[39] 张强, 赵齐乐. OpenMP并行计算在全球电离层反演中的应用[J]. 武汉大学学报(信息科学版), 2018, 43(2): 227-233, 240.

[40] Kuang K F, Zhang S J, Li J C. Real-time GPS satellite orbit and clock estimation based on OpenMP[J]. Advances in Space Research, 2019, 63(8): 2378-2386.

[41] Jiang C H, Xu T H, Du Y J, et al. A parallel equivalence algorithm based on MPI for GNSS data processing[J]. Journal of Spatial Science, 2021, 66(3): 513-532.

[42] Bertiger W, Bar-Sever Y, Dorsey A, et al. GipsyX/RTGx, a new tool set for space geodetic operations and research[J]. Advances in Space Research, 2020, 66(3): 469-489.

[43] Teunissen P J G. Quality control in navigation systems[J]. IEEE Aerospace and Electronic Systems Magazine, 1990, 5(7): 35-41.

[44] 杨元喜. 自适应动态导航定位[M]. 北京: 测绘出版社, 2006: 194-252.

[45] 范磊. 北斗/GNSS实时高效精密定轨及频间时钟偏差特性研究[D]. 武汉: 武汉大学, 2017.

[46] Li B F, Zhang Z T, Shen Y Z, et al. A procedure for the significance testing of unmodeled errors in GNSS observations[J]. Journal of Geodesy, 2018, 92(10): 1171-1186.

[47] 章浙涛. GNSS非模型化误差处理理论与方法[J]. 测绘学报, 2020, 49(7): 936-936.

[48] Kaselimi M, Voulodimos A, Doulamis N, et al. A causal long short-term memory sequence to sequence model for TEC prediction using GNSS observations[J]. Remote Sensing, 2020, 12(9): 1354.

[49] Kim H, Bae T. Deep learning-based GNSS network-based real-time kinematic improvement for autonomous ground vehicle navigation[J]. Journal of Sensors, 2019(6): 1-8.

[50] Ngoc T, Ali K, Fabrice C, et al. Robust-extended Kalman filter and long short-term memory combination to enhance the quality of single point positioning[J]. Applied Sciences, 2020, 10(12): 4335.

[51] 朱彬, 杨诚, 刘岩. GNSS多径信号3种非监督学习法分析与比较[J]. 测绘学报, 2021, 50(12): 1762-1771.

Discussion on development and solution of multi-frequency and multi-GNSS huge networks

LI Linyang1,2, LAI Luguang2, SHEN Yang2, DONG Hang3, LIN Jiale4

（1. School of Geodesy and Geomatics, Wuhan University, Wuhan 430072, China;2. School of Surveying and Mapping, Information Engineering University, Zhengzhou 450001, China;3. Troops 61206, Beijing 100041, China; 4. Troops 61081, Beijing 100089, China）

In order to further enhance the accuracy, integrity, continuity and availability of global navigation satellite system (GNSS) services, the paper analyzed and discussed the characteristics, difficulties and methods of solving multi-frequency and multi-GNSS huge networks: the latest development of multi-frequency and multi-GNSS huge networks was concluded from the aspects of space segment and ground segment; then the characteristic and difficulties of the solution were analyzed, and a unified processing model and corresponding high precision, high efficiency and intelligent solution algorithm were urgently needed; finally, the solution methods were summarized from the aspects of undifferenced model, parallel processing and intelligent resolution.

global navigation satellite system (GNSS); multi-frequency and multi-system; huge network solution

P228

A

2095-4999(2023)02-0028-08

李林阳, 赖路广, 沈洋, 等. 多频多GNSS大网发展与解算探讨[J]. 导航定位学报, 2023, 11(2): 28-35.（LI Linyang, LAI Luguang, SHEN Yang, et al. Discussion on development and solution of multi-frequency and multi-GNSS huge networks[J]. Journal of Navigation and Positioning, 2023, 11(2): 28-35.）DOI:10.16547/j.cnki.10-1096.20230204.

2022-05-30

国家自然科学基金项目（42104033）；河南省重点研发与推广专项（科技攻关）（212102310428）。

李林阳（1991—），男，河南确山人，博士，副教授，研究方向为时空基准精化与维持。

林家乐（1995—），男，辽宁丹东人，硕士，工程师，研究方向为时空基准精化与维持。