量子定位系统中的卫星间链路超前瞄准角跟踪补偿
汪泳钦,丛 爽
量子定位系统中的卫星间链路超前瞄准角跟踪补偿
汪泳钦,丛 爽
(中国科学技术大学 自动化系,合肥 230027)
为了进一步提高量子定位系统的精度,根据量子定位系统中发射端卫星和接收端卫星均在运动的情况,提出一种卫星间链路的超前瞄准角跟踪补偿方法:分析在量子导航定位系统中不同链路的超前瞄准角跟踪补偿情况,并对各自特点进行对比;再根据卫星轨道坐标系下发射端卫星和接收端卫星的位置计算地心惯性系下2颗卫星的相对位置,转换到卫星星上俯仰坐标系计算出超前瞄准角,并分析超前瞄准点在精跟踪探测器中的坐标转换关系;然后根据反射镜有效反射面积计算超前瞄准角对链路中量子接收效率的影响;最后,设计补偿方案并采用矩阵实验室(MATLAB)进行卫星轨道和超前瞄准角仿真,计算出需要补偿的随时间变化的方位角和俯仰角。
量子定位系统;卫星间链路;超前瞄准角;卫星轨道;跟踪补偿
0 引言
在星地量子定位系统中,发射的量子纠缠光发散角度很小,仅为十几微弧度,且光束对准跟踪精度要求小于几微弧度。为了能够实现星地间光链路的高精度对准,需要建立一套捕获、跟踪和瞄准(acquisition tracking pointing,ATP)系统用以实现对光链路的建立及保持:捕获是指双方在建立光链路前,发射端发送信标光,使接收端探测到该信标光,作为构建光链路的引导;跟踪是指将对方发射的信标光通过跟踪系统引导到跟踪探测器的中心位置,确保接收光路的对准;瞄准是指让信号光精准地指向对方,并保持高精度稳定[1]。星地量子定位系统光链路的建立及维持,通过发射端和接收端的ATP系统进行双向跟踪实现。ATP系统完成目标的跟踪并建立光链路后,由纠缠光发生器发射量子纠缠光进行测距。目前产生量子纠缠光源的方法有多种,其中自发参量下转换是一种比较常用的方法,它是由单色泵浦光子流和量子真空噪声对非中心对称非线性晶体的综合作用而产生的一种非经典光场。参量下转换过程为当激光入射到一个非线性晶体上时,非线性晶体的二阶非线性分量会使入射的光子以一定的概率劈裂为2个能量较低的光子。此双光子在能量、时间、偏振态上具有高度的纠缠特性,且产生的光场具有宽带光谱分布的特点。基于3颗量子卫星实现对用户的定位,当其工作于星基模式时,其定位过程为[2]:卫星上的纠缠光子对发生器发射2束纠缠光,其中一束沿星地光链路到达用户,并从用户处反射回卫星,被卫星上的一个单光子探测器接收;另一束直接发射向卫星上的另一个单光子探测器,完成纠缠光子对的发射与接收。此时卫星内部直接发射向单光子探测器的纠缠光一直在卫星内部,利用2路纠缠光的到达时间差计算出的2路纠缠光的光程差是卫星与地面距离的2倍;再根据3颗卫星得到的3个到达时间差,分别计算出3颗卫星到用户的距离;然后通过联立解算所获得的3个距离方程计算出用户的空间坐标。量子定位系统中的定位精度主要依赖于ATP系统的跟踪精度。ATP系统主要是由粗跟踪模块、精跟踪模块以及超前瞄准模块组成,原理如图1所示[2],其中,粗跟踪模块主要完成目标的捕获和粗跟踪。典型的粗跟踪模块结构主要包括万向架以及安装在上面的收发光学天线、分束器、粗跟踪探测器、粗跟踪控制器、万向架、角传感器以及伺服机构;精跟踪模块在粗跟踪模块的跟踪误差基础上进一步提高精度,结构主要包括二轴快速反射镜、精跟踪探测器、精跟踪控制器、执行机构和位置传感器。
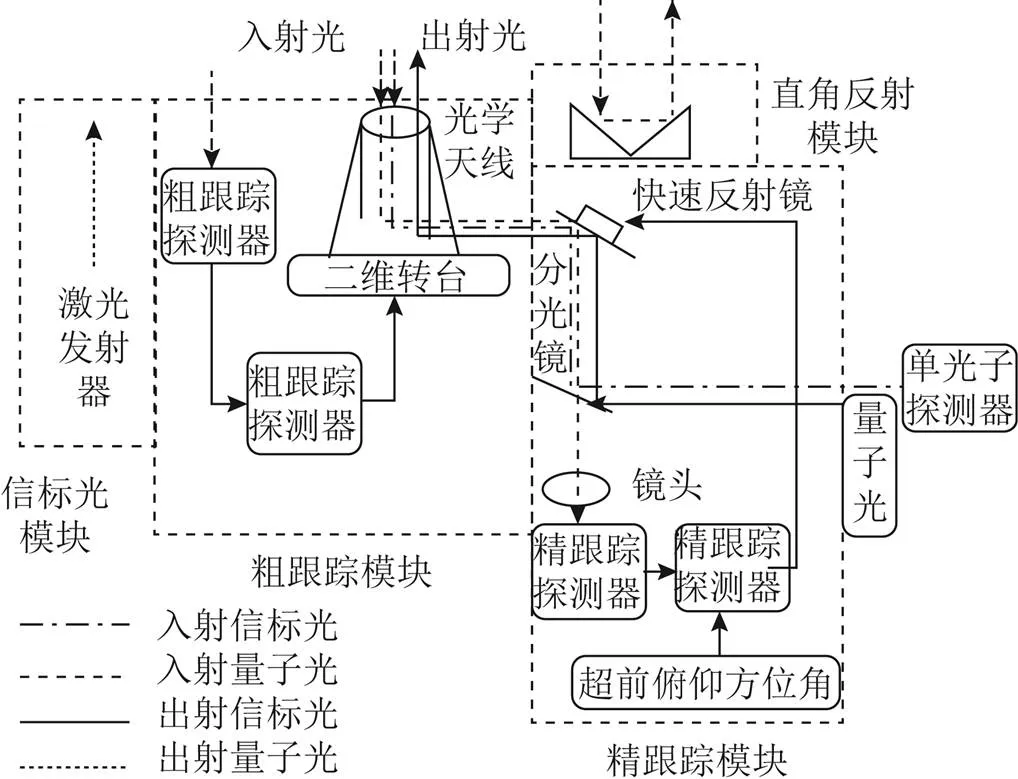
图1 ATP系统的结构
在ATP系统中,为了能够使得发射端发射出的量子光被运动的接收端准确接收,所发射量子光的发射角度需要沿着接收端的运动方向,超前入射信标光一定的角度,这个角度被称为超前瞄准角。超前瞄准模块主要补偿由于光束远距离传输引起的位置偏差,使出射光相对于接收光偏转指定的角度,从而使出射光精确瞄准对方[3]。在ATP系统的运行过程中,粗跟踪模块用于在视场中找到目标,然后精跟踪模块对目标进行精确跟踪,再由超前瞄准模块补偿发射时的偏转角度。超前瞄准模块是ATP系统的重要组成部分,它用于补偿发射端和接收端之间由于相对运动造成的瞄准角度偏差。当瞄准角度偏差过大时,接收端可能偏离跟踪视场,直接导致系统性能恶化, 严重时甚至会造成通信链路中断。因此,超前瞄准角度偏差的补偿,能有效地保持链路的稳定性,提高系统的跟踪精度与定位精度[4]。2017年,文献[5]通过航天器动力学轨道模型研究激光瞄准系统跟踪运动目标的超前瞄准角变化特性,并分析了目标的角速度和角加速度等对超前瞄准角的影响。2019年,文献[6]研究了卫星间光通信的超前瞄准角,并对低轨道卫星和同步轨道卫星之间激光通信的超前瞄准角进行了仿真。超前瞄准模块有2种实现方案:1)通过设计额外的超前瞄准子系统来实现,由超前瞄准镜、超前瞄准探测器以及超前瞄准控制器3个部分组成[7];2)采用基于精跟踪模块的实现方法[8]。由于使用独立的超前瞄准子系统实现量子纠缠光的超前瞄准方案增加了终端重量和ATP系统的复杂度,本研究组设计研究了星地间的超前瞄准角度的补偿系统[9],本文将采用第二种,即基于精跟踪模块方法来实现低轨道卫星间链路的超前瞄准角度的补偿。
1 量子定位系统分类及对应的超前瞄准角
目前量子定位系统能够基于3颗卫星实现目标定位[10]。基于3颗卫星的量子定位系统有2种定位方式,即星基量子定位和地基量子定位,如图2所示。星基量子定位通过卫星向地面目标和其他卫星发射量子纠缠光获取位置参数信息,而地基量子定位则通过地面站向3颗卫星分别发射量子纠缠光获取位置参数信息。地基量子定位通过地面站发射量子纠缠光,地面站固定不动,所以该定位方法中超前瞄准角的计算相对简单。但星基量子定位中,发射量子纠缠光的卫星处于运动状态,接收量子纠缠光的卫星也处于运动状态,2颗卫星均要影响超前瞄准角的计算,定位过程更加复杂。
量子定位系统的发射端结构包括纠缠光源系统、接收系统、ATP系统以及信号处理系统。纠缠光源系统包括纠缠光发生器、滤波片等,接收系统包括接收望远镜、单光子探测器、符合计数器等,ATP系统包括粗跟踪模块、精跟踪模块以及超前瞄准模块,信号处理系统包括信号接收模块以及数据结算模块。接收端结构包括ATP系统和反射系统,反射系统通常为反射镜或角锥反射器[11-12]。当发射端处于移动状态时,需要通过对反射镜的角度进行微调,使反射的回波信号回到接收系统中[13]。
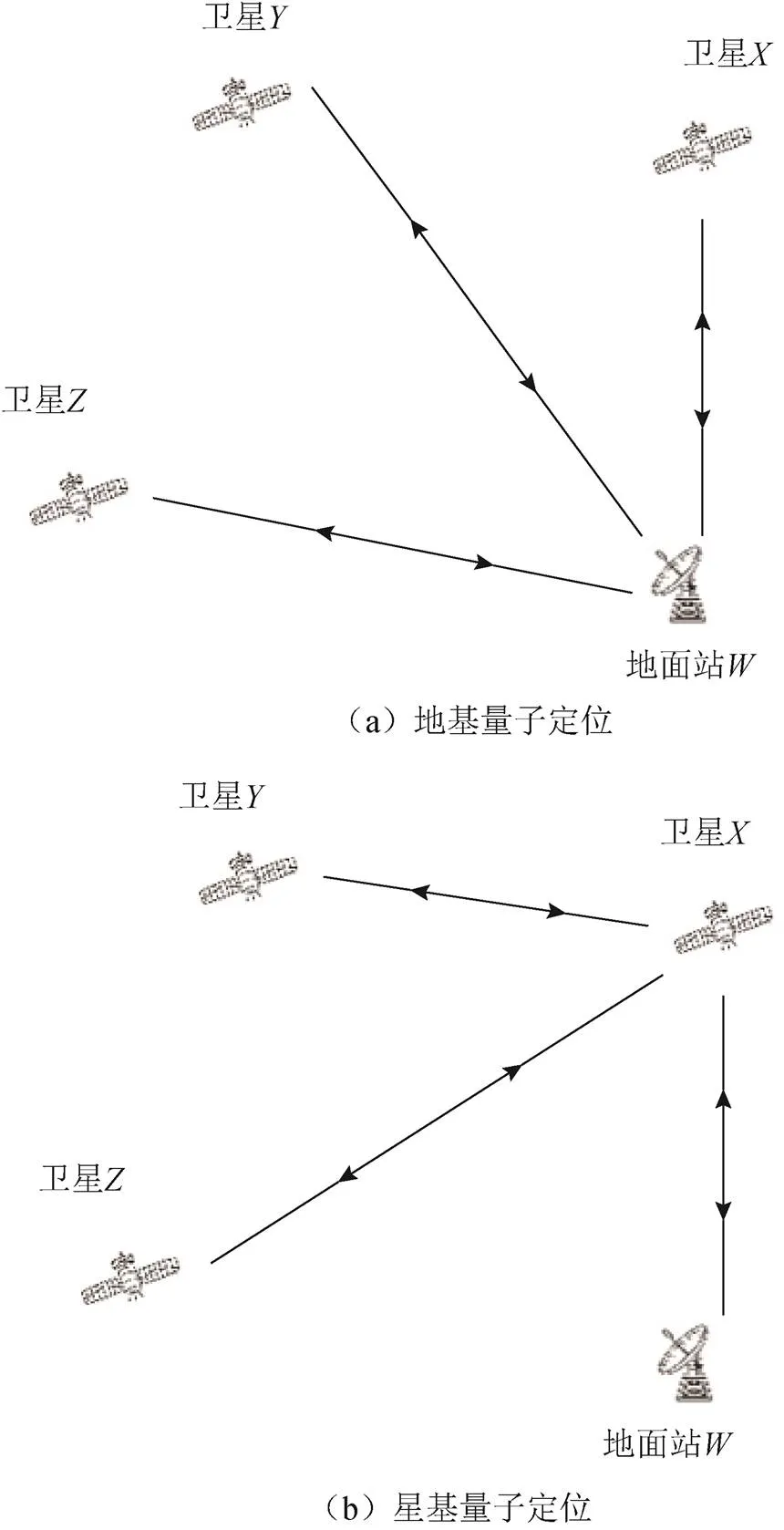
图2 2种量子定位方式的原理
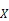
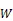

图3 地面—卫星链路情况下的超前瞄准角情况

图4 星基量子定位的超前瞄准角情况
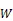
星基量子定位和地基量子定位超前瞄准角情况主要的不同点有:
1)星基量子定位中,卫星间链路需要考虑2颗卫星的运动轨迹,综合得到超前瞄准角。而卫星—地面链路和地基量子定位的地面卫星链路,只需要考虑1颗卫星的运动轨迹。
2)星基量子定位中,需要将地心惯性系转换到卫星星上俯仰坐标系来计算超前瞄准角。而地基量子定位中只需要在地心惯性系下计算超前瞄准角。
3)星基量子定位卫星间链路不需要考虑大气的影响,而卫星—地面链路和地面—卫星链路则需要考虑大气的影响。
本文主要研究卫星间链路的超前瞄准角度计算、对接收效率的影响及超前瞄准角跟踪的补偿。
2 量子定位中超前瞄准角的计算
在ATP系统中,为了补偿光束在传播时间内双方的相对位移引起的超前瞄准角,需要将信标光(激光或纠缠光)或信号光(纠缠光)的发射角度沿着卫星运动方向,超前入射一定的角度,这个偏差的角度称为超前瞄准角[14]。
2.1 卫星间链路超前瞄准角的理论推导
2.2 超前瞄准角中的坐标系转换
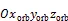

图5 3种卫星三维空间坐标系
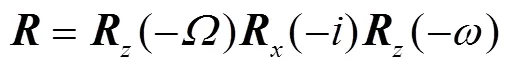
变换矩阵的具体形式为
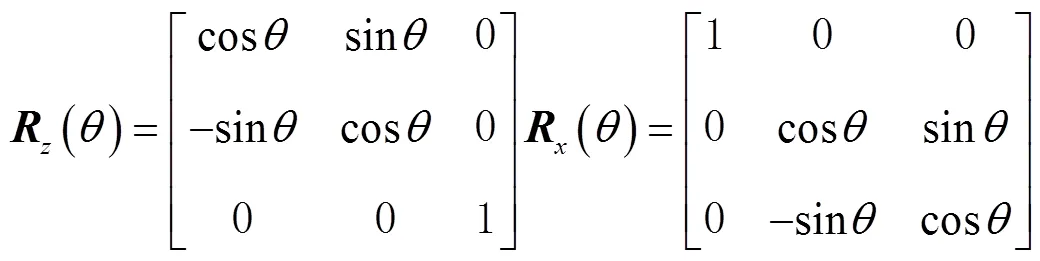
于是

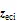
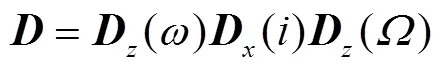
其中的变换矩阵具体形式为

于是
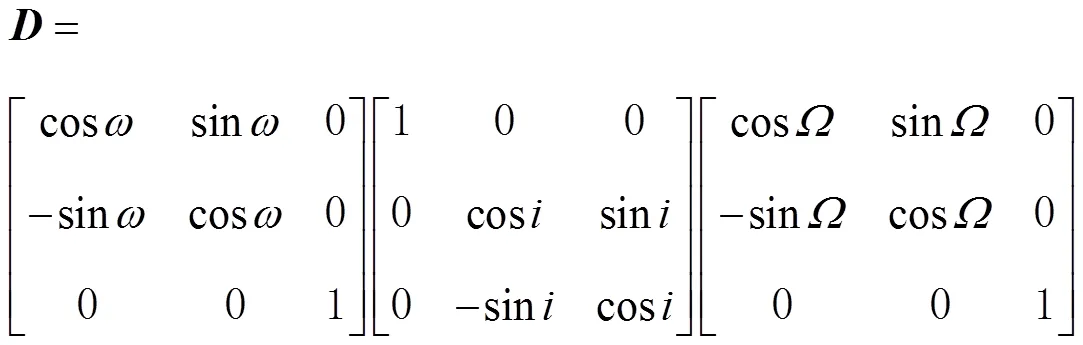
2.3 超前瞄准模块中俯仰角和方位角的计算
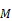

对于卫星间链路,求解方法如下:

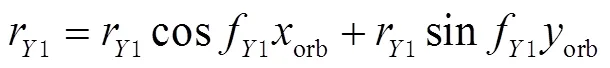
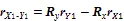
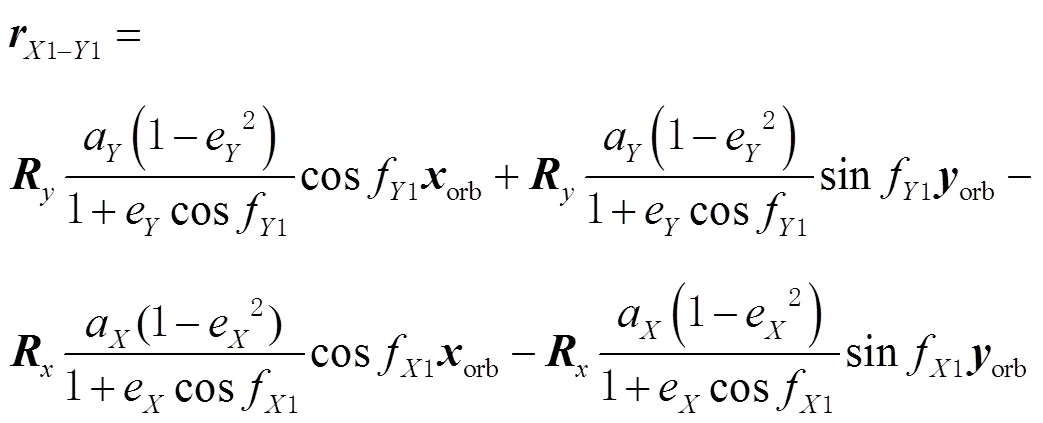
与地基量子定位中的超前瞄准角计算不同,还需要将相对位置矢量转换到发射端卫星星上俯仰坐标系,可得变换后发射时的2颗卫星之间位置矢量


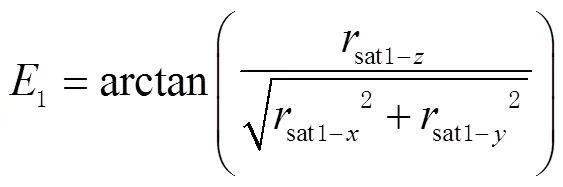
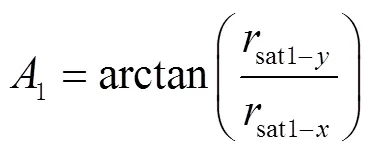
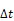
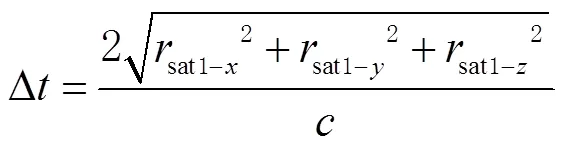

图4(b)中的超前瞄准角,在俯仰轴和方位轴的投影即为和,空间中的关系如图6所示,由点H向平面做垂线,垂足为I,J为x轴上一点,∠HOJ余弦值等于。
3 超前瞄准角在卫星探测器方位俯仰角的转换
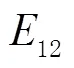
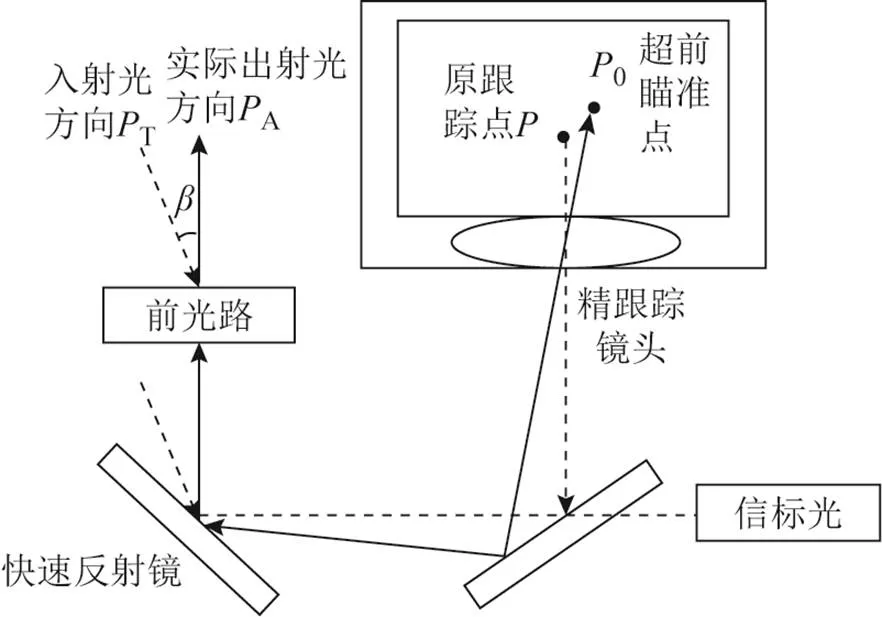
图7 基于精跟踪的超前瞄准角跟踪补偿
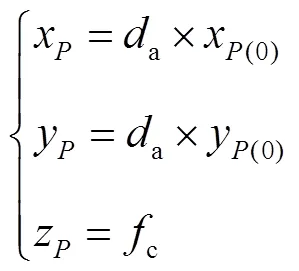
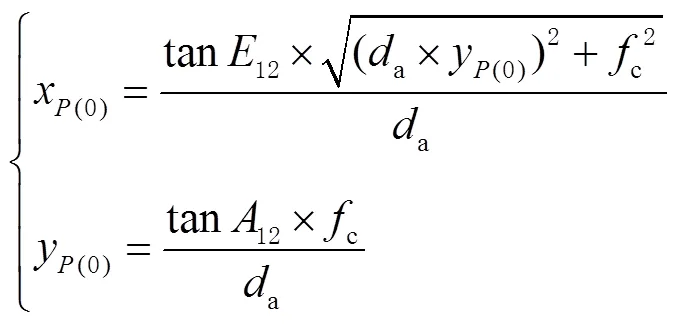
图8 探测器视场的二维坐标系与探测器镜头的三维坐标系


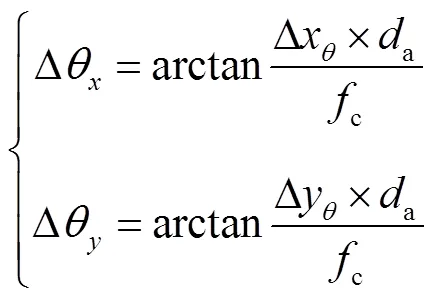
式(21)计算出的就是卫星探测器坐标系下,在每一个时刻,卫星所在位置需要补偿的角度。在本文的超前瞄准角补偿系统仿真中,将该角度和粗跟踪误差一起输入到粗跟踪模块进行轨迹跟踪。
4 超前瞄准角对接收效率的影响分析
在量子定位系统中,信号光为纠缠单光子,其发散角小、光强弱,不能同时作为信标光和信号光,所以ATP系统的信标光需要使用激光。在我们的实验中,ATP系统采用凝视-扫描技术进行指向,其捕获过程如图9所示。最初发射端与接收端之间没有对准,接收端视场中心与发射端信标光中心之间存在初始偏置角。发射端通过一定的顺序扫描不确定区域(field of uncertainty,FOU),接收端的接收视场(field of view,FOV)大于不确定域和发射端光束的发散角,当接收到发射端发射的信标光时,及时发送回波信号,建立连接,之后开始跟踪过程。
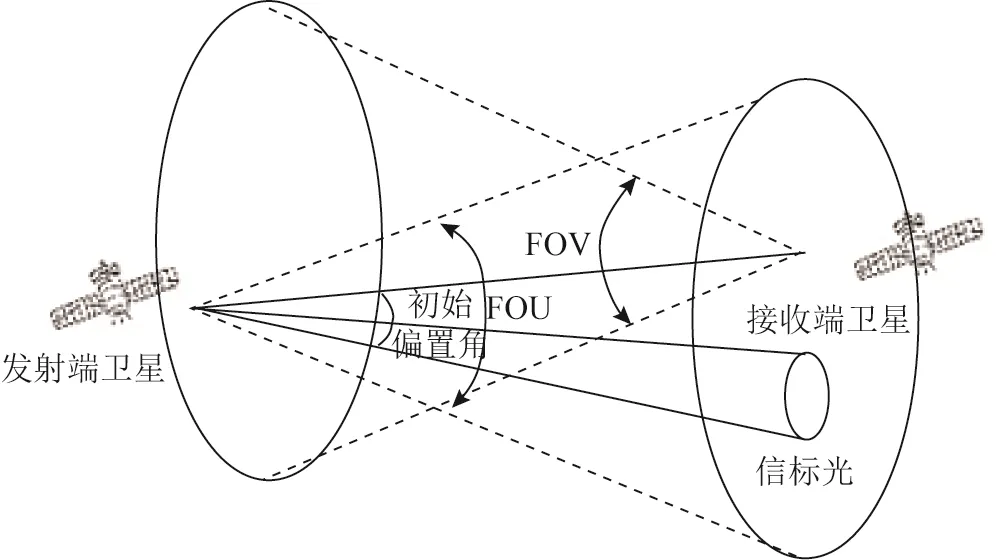
图9 凝视-扫描技术捕获过程[16]
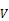
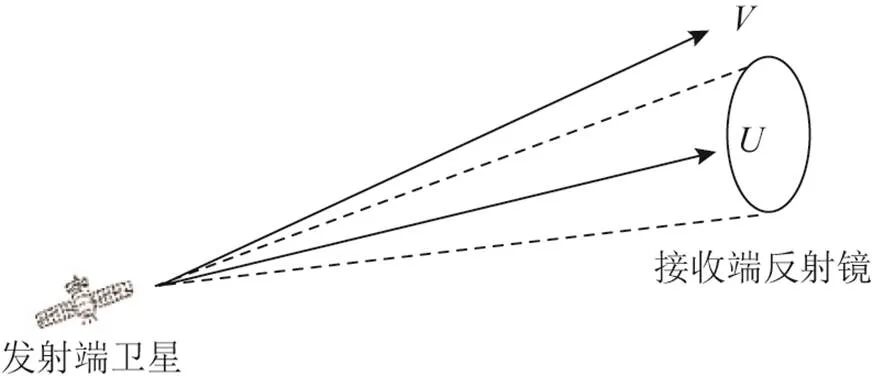
图10 信号光发散角与反射镜的关系
实际中信号光的接收效率的计算公式为

由式(22)可以得出,通过增大反射镜的半径、减小纠缠光发散角、增加发射纠缠光的频率等方法,也可以提高接收效率。
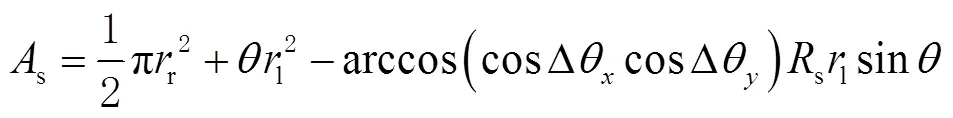

5 实验与结果分析
5.1 量子定位ATP系统的实现
粗跟踪模块采用三环控制结构,每一环均采用比例、积分、微分(proportional,integral and derivative, PID)控制。从内而外依次为电流环、速度环和位置环,被控对象为电机。其中,电流环根据电机的电枢电流作为反馈量;速度环采用角度传感器测量电机的角度,并差分求出电机速度作为反馈量;位置环由粗跟踪探测器获得的光斑位置与探测器的中心偏差作为反馈量[2]。电流环经过等效后可以简化为比例环节,速度环采用 PI 控制器进行控制,而位置环采用 PID 控制器进行控制,其控制器参数选择如表1所示[17]。

表1 粗跟踪控制器参数
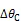

表2 精跟踪控制器参数
5.2 超前瞄准角跟踪补偿方案

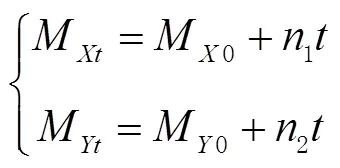

表3 发射端卫星“墨子号”参数


表4 接收端卫星GRACE-2参数

图11 发射端与接受端的距离变化曲线
由图可知,卫星间距离在几百千米到一万几千千米之间。由于卫星轨道半径在地面上空500 km左右,故近地卫星间链路的距离一般在5000 km以内,否则地球会遮挡卫星间的跟踪链路;所以截取2700~3400 s这段时间,该段时间2颗卫星间距离始终保持在5000 km以下。超前瞄准角的俯仰角和方位角的变化如图12所示。
在这段时间内,根据式(15)可以得到光束的弛豫时间,进而根据式(16)可以求得每个时刻超前瞄准角的俯仰角和方位角曲线(如图13所示)。
由图可以看出,超前瞄准角俯仰角的大小在-20到40 μrad之间,方位角最大为84.7 μrad。然后根据式(21)可以将得到的超前俯仰角及方位角转换为精跟踪动态中心的调整量,其中,精跟踪探测器镜头焦距取=1000 mm,可以得到精跟踪中心调整量变化曲线(如图14所示)。

图12 观测时间内俯仰角和方位角的变化

图13 观测时间内超前瞄准角的俯仰角和方位角变化
从图可以看出,方向调整量范围大于方向调整量,且最大需要调整的像素数目大约为 0.09 mrad。粗跟踪的视场为3 mrad×3 mrad,精跟踪的视场为0.5 mrad×0.5 mrad,调整量能够被精跟踪视场所容纳,可以在精跟踪视场中动态调整跟踪中心。理论上不需要额外的补偿即可跟踪考虑了超前瞄准角情况下的卫星。

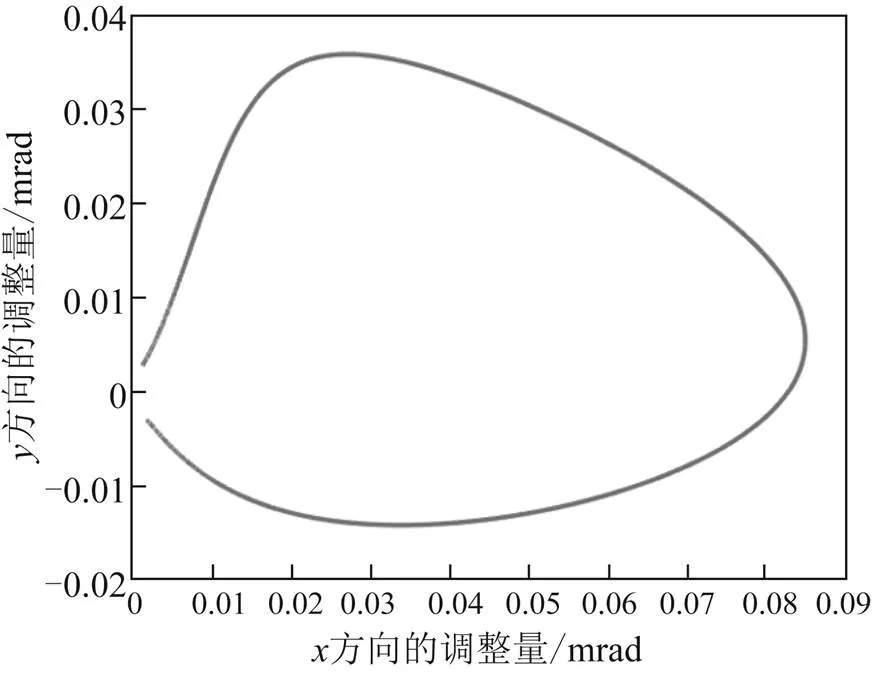
图14 精跟踪中心调整量变化曲线
6 结束语
本文研究了量子定位系统中发射端卫星和接收端卫星均在运动时,卫星间链路的超前瞄准角跟踪补偿。与地面—卫星链路不同,卫星间链路需要考虑2颗卫星各自的运动轨迹,并从地心惯性系转换到卫星星上俯仰坐标系来计算超前瞄准角。文中运用卫星轨道坐标系、地心惯性系、卫星星上俯仰坐标系3个系之间的坐标变换,计算了卫星间链路的超前瞄准角大小,然后分析了超前瞄准点在精跟踪探测器中的坐标转换关系。根据量子接收效率公式可以得到,超前瞄准角的跟踪补偿能够有效提高反射面积,进而提高接收效率。最后,在给定的粗精跟踪系统参数下设计了补偿方案,将超前瞄准角加入粗跟踪系统进行补偿,使量子定位系统的精度进一步提高。通过MATLAB进行了卫星轨道和超前瞄准角仿真,验证了精跟踪视场能够实现超前瞄准角跟踪补偿的可行性。
[1] 王娟娟. 基于GPS/INS运动二维转台的指向技术研究[D]. 济南:山东大学, 2014.
[2] 丛爽, 王海涛, 陈鼎. 量子导航定位系统[M]. 合肥:中国科学技术大学出版社, 2021.
[3] 丛爽, 汪海伦, 邹紫盛, 等. 量子导航定位系统中的捕获和粗跟踪技术[J]. 空间控制技术与应用, 2017, 43(1): 1-10.
[4] 叶德茂, 谢利民, 陈晶. 跟踪误差补偿下星地光通信地面模拟实验分析[J]. 激光技术, 2012, 36(3): 346-348.
[5] 叶小威, 沈锋. 航天器轨道动力学模型及瞄准提前量误差分析[J]. 中国激光, 2017, 44(6): 196-206.
[6] 李伯良. 提前瞄准角度变化对星间光通信系统性能影响研究[D]. 哈尔滨:哈尔滨工业大学, 2019.
[7] TAKASHI J. Optical Inter-orbit communication experiment between OICETS and ARTEMIS[J]. Journal of the National Institute of Information and Communications Technology, 2012, 59(1/2): 23-33.
[8] 梁延鹏. 星地光通信ATP对准特性仿真研究[D]. 合肥:中国科学技术大学, 2014.
[9] CONG S, ZHANG X, DUAN S Q. Design and simulation of the ATP system considering the advanced targeting angle in quantum positioning system[J]. System Engineering&Electronics Technology, 2022, 33(5): 1-11.
[10] 丛爽, 陈鼎, 宋媛媛, 等. 一种基于三颗量子卫星的定位与导航方法及系统: 201711465970.9[P]. 2020-02-18.
[11] 汪海伦, 丛爽, 尚伟伟, 等. 量子导航定位系统中光学信号传输系统设计[J]. 量子电子学报, 2018, 35(6):714-722.
[12] 张海峰, 程志, 恩李朴, 等. 纳卫星激光反射器光机设计及激光测距分析[J]. 飞行器测控学报, 2016, 35(1): 21-27.
[13] 罗青山. 皮纳微小卫星激光反射器设计及激光测距分析[J]. 国际地震动态, 2019(2): 46-47.
[14] 刘智颖, 付跃刚. 新型光通信提前量检测系统的设计[J]. 仪器仪表学报, 2006, 27(6): 690-691.
[15] KOZAI Y. The motion of a close earth satellite[J]. The Astronomical Journal, 1959, 64(8): 337.
[16] 董全睿. 基于高精度跟瞄系统的扰动补偿控制技术研究[D]. 长春: 中国科学院大学(中国科学院长春光学精密机械与物理研究所), 2020.
[17] 段士奇. 基于卫星的量子测距系统仿真平台的设计与实现[D]. 合肥: 中国科学技术大学, 2021.
[18] 丛爽, 邹紫盛, 尚伟伟, 等. 量子定位系统中的精跟踪系统与超前瞄准系统[J]. 空间电子技术, 2017, 14(6): 8-19.
[19] 邹紫盛. 量子定位中精跟踪系统滤波与控制研究[D]. 合肥:中国科学技术大学, 2019.
[20] 段士奇, 丛爽, 邹子盛, 等. 量子导航定位系统中ATP子系统的仿真研究[C]//第二十届中国系统仿真技术及其应用学术年会论文集. 乌鲁木齐: 中国科学技术大学出版社, 2019: 234-239.
[21] 丛爽, 段士奇. 基于量子卫星“墨子号”的量子测距过程仿真实验研究[J]. 系统仿真学报, 2021, 33(2): 377-388.
Tracking compensation of inter satellite link point ahead angle in quantum positioning system
WANG Yongqin, CONG Shuang
(Department of Automation, University of Science and Technology of China, Hefei 230027, China)
In order to further improve the accuracy of the quantum positioning system, in view of the situation that both the transmitting satellite and the receiving satellite are moving in the quantum positioning system, the paper proposed a tracking compensation method of the inter satellite link point ahead angle: the tracking compensation status of point ahead angles of different links in quantum navigation and positioning system was analyzed, and their characteristics were compared; and the relative positions of the two satellites in the geocentric inertial system were calculated according to the positions of the transmitting and receiving satellites in the satellite orbital coordinate system, then converted into the satellite on-board pitch coordinate system to calculate the point ahead angle of the inter satellites link, and the coordinate transformation relationship of the point ahead dot in the precision tracking detector was analyzed; next, the impact of the point ahead angle on the quantum receiving efficiency in the link based on the effective reflection area of the reflector was calculated; finally, the compensation scheme was designed, and the satellite orbit and the point ahead angle were simulated by MATLAB, and the azimuth and pitch angles that need to be compensated over time were calculated.
quantum positioning system; inter satellite link; point ahead angle; satellite orbit; tracking compensation
P228
A
2095-4999(2023)02-0080-12
汪泳钦, 丛爽. 量子定位系统中的卫星间链路超前瞄准角跟踪补偿[J]. 导航定位学报, 2023, 11(2): 80-91.(WANG Yongqin, CONG Shuang. Tracking compensation of inter satellite link point ahead angle in quantum positioning system[J]. Journal of Navigation and Positioning, 2023, 11(2): 80-91.)DOI:10.16547/j.cnki.10-1096.20230209.
2022-03-30
国家自然科学基金项目(61973290)。
汪泳钦(1998—),四川成都人,硕士研究生,研究方向为量子导航定位等。

