数学核心素养测评之调查问卷的统计分析

胡典顺　骆仁轩

胡典顺 华中师范大学数学与统计学学院教授、博士研究生导师，华中师范大学数学教育教研室主任，湖北省中学数学教学指导委员会副主任委员；《数学教育学报》《数学通讯》编委，鄂教版高中数学教材（2019年版）副主编，中国国际文化交流基金会第三届“明德教师奖”获得者；曾以访问学者的身份，由国家留学基金委公派访问美国特拉华大学；在《课程·教材·教法》《中国教育学刊》《数学教育学报》《教育科学研究》等期刊上发表论文270余篇，出版《基于数学意义的数学教学改革研究》《整合技术的学科教学知识：从教师专业素养到教师教学实践》《中学生数学素养测评的模型建构与实证研究》等专著，主持多项全国教育科学规划项目和教育部人文社会科学研究规划基金项目。

数据统计分析有三个层次：描述性统计、差异性分析和统计模型。本文基于“WJ市義务教育核心素养监测”项目，对数学核心素养测评调查问卷结果的描述性统计内容、相关分析内容以及如何利用统计分析软件如SPSS 26.0进行描述性统计、差异性分析和相关分析，做具体阐述。

一、描述性统计的内容

描述性统计主要包括数据的频数分析、集中趋势分析、离散程度分析，以及绘制基本的统计图等。本项目中，笔者通过制作表格、绘制统计图等可视化形式，对学生的数学学习情况、数学学习价值观、数学学习品格等调查维度得分的频数、集中趋势和离散程度等进行分析。

1.频数分析

频数分析是对一组数据不同取值的频数或者取值落入指定区域内的频数进行统计分析。频数分析能够帮助我们了解数据的分布特征。实际运用中，一般也会计算出每个频数对应的频率。例如，“学生的数学学习价值观”维度有一个问题为“数学知识与我们的生活联系紧密，数学是很有用的学科”，此题采用7级量表测量，可以通过统计第1～7项得分的频数和频率，了解学生对数学知识的态度的分布情况。

2.集中趋势分析

集中趋势分析是对反映数据水平的代表值或中心值进行统计分析。常用的统计量有算术平均值（以下简称“均值”）、众数和中位数等。例如，“学生的数学活动参与情况”维度有一个问题为“我经常和同学一起讨论数学题”，此题采用7级量表测量，计算学生得分的均值，可以了解学生和同学讨论数学题的集中趋势。此均值越高，说明有越多学生倾向于和同学一起讨论数学题。

3.离散程度分析

离散程度分析是对数据之间的差异程度进行统计分析。常用的统计量有方差、标准差、平均值标准误差、极差等。例如，“学生的数学学习动机”维度有一个问题为“学数学时，我感到很快乐”，此题采用7级量表测量，计算学生得分的标准差、平均值标准误差、最大值以及最小值等，可以了解学生学习数学的快乐程度是否分散。

4.常用统计图

描述性统计常用的统计图有条形统计图、折线统计图、雷达图、箱图等，研究者可以根据需要选择。在调查问卷的描述性统计中，一般分别对调查的各个维度进行分析。以“数学教师情况”维度的描述性统计为例。如果研究者想了解学生问卷得分的均值和频数以及对应的频率，就可以在统计出相应数据之后列出表格。为了更直观地研究数据的变化情况，研究者可以根据需要基于列出的表格绘制统计图，并结合表格和统计图对统计结果进行解释。

二、相关分析的内容

相关分析是对两个或两个以上变量之间的相关程度进行统计分析，以确定相关关系的存在、相关关系呈现的形态和方向、相关关系的密切程度，主要方法有绘制相关表、相关散点图和计算相关系数。研究者常用计算相关系数进行相关分析。相关系数有很多种，如皮尔逊相关系数、肯德尔相关系数和斯皮尔曼相关系数等。其中，皮尔逊相关系数r被广泛应用于度量两个变量之间线性相关的程度。r的取值范围是[-1，1]。r越接近1，两个变量的正线性相关程度越强；r越接近-1，两个变量的负线性相关程度越强；r越接近0，两个变量的线性相关程度越弱。在根据r的取值判定相关关系的密切程度时，通常的划分标准为：|r|<0.3，视为无线性相关；|r|在0.3～0.5间，视为低度线性相关；|r|在0.5～0.8间，视为中度线性相关；|r|>0.8，则是高度线性相关。线性相关关系只能反映两个变量之间的线性相关性，不能反映因果性。例如，有研究表明学生的学习成绩与学习动机有线性相关关系，但这不一定说明它们之间有因果关系，因为学生的学习成绩可能还会受到教师的教学水平、学生的知识储备等的影响。

研究者如果想研究“数学教师情况”和“学生的数学学习情况”的线性相关程度，就可以将每名学生在两个维度的得分视为代表相应维度的两组变量，计算这两组变量的皮尔逊相关系数，最后根据所得的皮尔逊相关系数判断这两个维度之间的线性相关程度。对涉及某个维度整体的分析，可将学生在此维度所有题目的总分或者得分均值作为学生在此维度的得分。

三、描述性统计、差异性分析及相关分析举隅

参与本次抽样调查的学生有4134人，其中有效问卷4014份。以“数学教师情况”维度的5道题目（下列是关于你的数学老师的说法，请在符合你实际情况的选项下打“√”：①教学经验丰富；②性格开朗；③与我们关系融洽；④上课能吸引我的注意力；⑤促进了我的数学学习）为例。该部分题目以7级量表呈现，按照越符合得分越高的规则赋分，即从“完全符合”到“完全不符合”依次从赋7分到赋1分。

1.频数分析

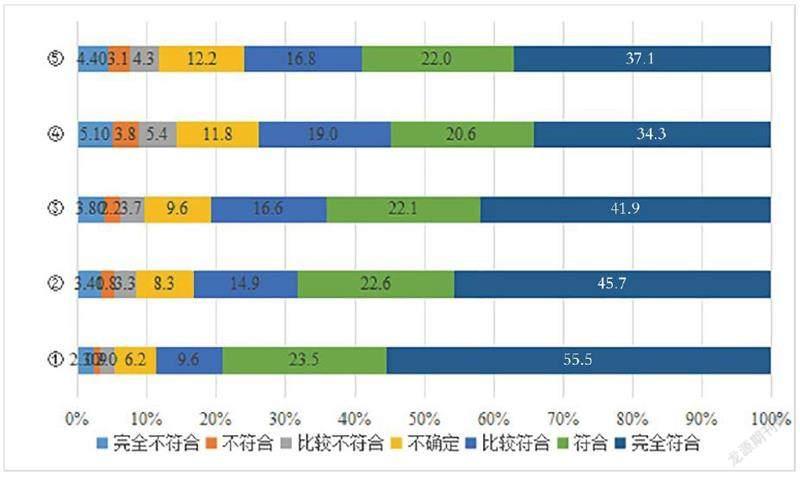
用SPSS 26.0对这5道题目进行频数分析，要先根据调查数据建构数据文件，再执行如下操作：①选择【分析】→【描述统计】→【频率】，将这5道题放入【变量】对话框，选中【显示频率表】，点击【确定】运行。这样就可得出每道题每个选项的得分频数和百分比。为了更直观地反映统计结果，可将反映百分比的数据用条形统计图（如下图）显示。

以第①题为例分析，由图可知，选择“比较符合”“符合”和“完全符合”的比重总和为88.6%，表明大部分学生都认为自己的数学老师教学经验丰富。

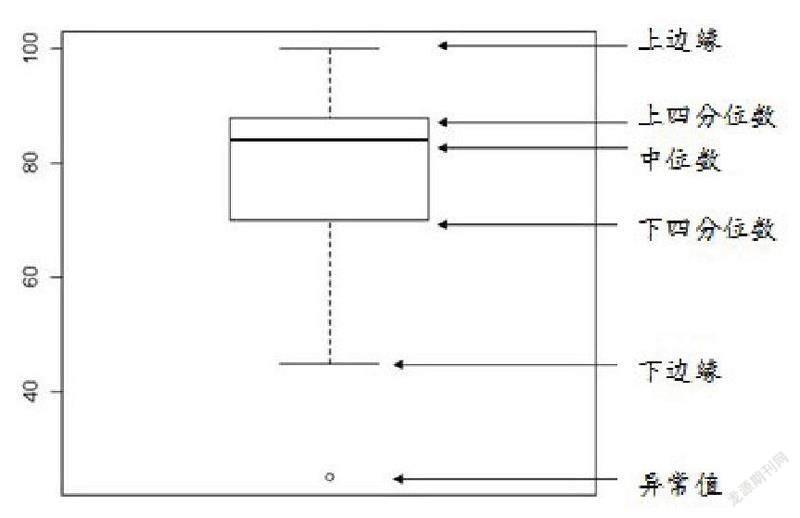
除了通过频数分析了解一组数据的基本分布情况，还可以利用箱图深入描述一组数据的分布情况。介绍箱图之前，要先了解第p百分位数的概念：一组数据中的第p百分位数指这组数据中至少有p%的数据小于或等于这个值，且至少有（100-p）%的数据大于或等于这个值。箱图（如下图）由中间的粗横线、一个方框、外延出的两条虚线（也可以为实线）和最外端可能存在的单独散点组成，可以表述一组数据的中位数、上四分位数（第75百分位数）、下四分位数（第25百分位数）、最小值（下边缘）和最大值（上边缘）等，可以反映数据是否具有对称性、数据分布的分散程度等，尤其是可以用于对比几个样本的分布情况。

箱图中，方框上端和下端分别表示上、下四分位数，上端与下端的距离为四分位差；与四分位数距离超过1.5倍四分位差的值被定义为异常值，处于1.5～3倍四分位差的异常值用空心圆表示，超过3倍四分位差的异常值用实心圆表示。统计软件会在异常值对应的圆旁边标上数字，以表示此异常值在数据集中的行数。

用SPSS 26.0对“数学教师情况”维度所得数据绘制箱图，先根据调查数据构建数据文件，再执行如下操作：①选择【转换】→【计算变量】，在【目标变量】中输入“数学教师情况总分”，在【数学表达式】中将学生作答该维度5道题目的得分相加，点击【确定】；②选择【图形】→【图表建构器】，点击【确定】进入主对话框；③在主对话框下方的【图库】→【选择范围】中点击【箱图】，双击“简单箱图”，将【变量】中的“数学教师性别”拖入“x轴”（“x轴”中可以不拖入变量，也可以根据需要拖入其他变量）、“数学教师情况总分”拖入“y轴”，点击【确定】运行。所得的“不同性别的数学教师情况”箱图（图略）显示，女教师得分的中位数比男教师高，男、女教师得分的四分位差比较接近且均较小，说明男、女教师得分分布都比较集中。同时，男、女教师得分都出现了一些异常值，值得研究者注意。

2.集中趋势和离散程度分析

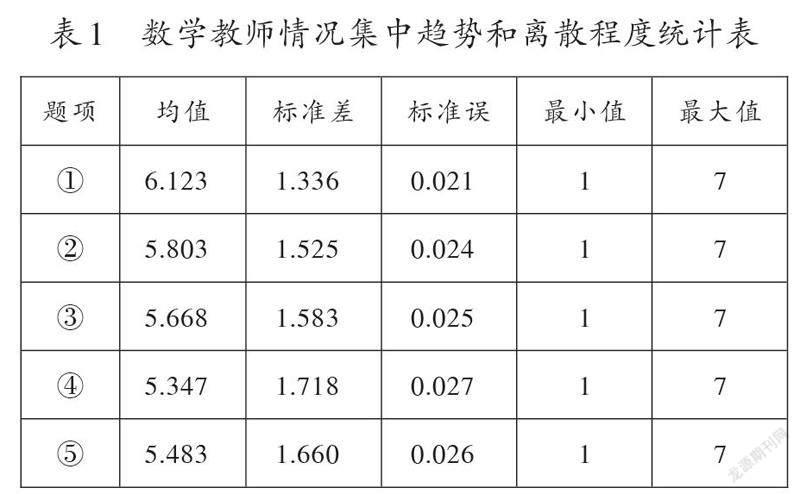
某个调查维度题目得分的频数、集中趋势和离散程度可以同时分析。用SPSS 26.0对“数学教师情况”维度的5道题目同时进行集中趋势分析和离散程度分析，先根据调查数据构建数据文件，再执行如下操作：①选择【分析】→【描述统计】→【频率】，将5道题目放入【变量】对话框；②点击【统计】→选中【平均值】【标准差】【最小值】【最大值】【标准误差平均值】（根据需要选择），点击【继续】，回到主对话框，点击【确定】运行。所得结果如表1所示。

由表1可知，在满分为7分的情况下，“数学教师情况”维度所有题目的得分均值都在5分以上，并且标准差、标准误都比较低，说明此维度数据测量比较准确，数据分散程度低，有比较多的学生认为自己的数学老师有较高的教育教学水平。

研究者往往会关心不同条件下某个维度得分均值的差异性，如男、女教师在“数学教师情况”维度得分均值的差异性。在研究该得分均值在统计学意义上的差异性之前，研究者通常会先利用描述性统计“探路”。如用SPSS 26.0对不同性别的数学教师在此维度的调查结果进行描述性统计，结果显示，女性数学教师的得分均值（29.125分）比男性（27.749分）高。描述性统计仅能说明男、女教师的得分均值在直觉上有一定差异，直觉不一定准确，因此男、女教师得分均值是否存在统计学意义上的差异仍需进一步通过差异性分析来验证。

3.差异性分析

簡而言之，差异性分析是对不同样本组的某个指标的差异进行分析。若不同样本组的某个指标存在统计学意义上的差异，则说明这些样本来自具有差异的不同总体，即这些样本组在某个指标上存在显著性差异。差异性分析常用的假设检验方法有t检验、方差分析等。对上述两组数据均值的差异性分析，适合使用独立样本t检验。若是涉及三组及三组以上数据均值的差异性分析，则要使用方差分析。

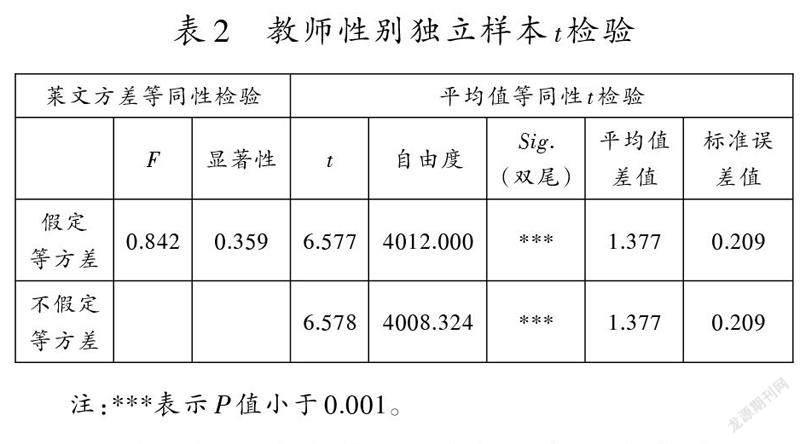
用SPSS 26.0对不同性别教师的“数学教师情况”维度得分均值进行差异性统计分析，先根据调查数据构建数据文件，再执行如下操作：①选择【分析】→【比较平均值】→【独立样本t检验】，将“数学教师情况总分”放入【检验变量】对话框，将“教师性别”放入【分组变量】对话框；②点击【定义组】，输入组1、组2对应的数字，即男、女教师在数据集中对应的值，点击【继续】→【确定】运行。所得结果如表2所示。

对表2中的检验结果，首先观察假定等方差所在行对应的显著性：若假定等方差所在行对应的显著性大于给定的显著性水平（一般为0.05），则说明两组数据的方差没有显著性差异，此后只需观察假定等方差所在行对应的数据；若假定等方差所在行对应的显著性小于给定的显著性水平，则要观察不假定等方差所在行对应的数据。无论观察哪行数据，若P值<0.05，则说明两组数据的均值存在显著性差异；若P值>0.05，则说明两组数据的均值不存在显著性差异。表2中假定等方差对应的显著性是0.359，因为0.359大于0.05，所以观察假定等方差所在行对应的P值。P值小于0.05，说明男、女教师在“数学教师情况”维度的得分均值存在显著性差异。

4.相关分析

由于皮尔逊相关系数表明的是两个变量间的线性相关程度，所以除了“数学教师情况”维度，还需要一个维度。选择“学生的数学学习情况”维度，该部分题目（请在符合你实际情况的选项下打“√”：①我的数学成绩在班级中是优秀的；②我目前数学学习状态好；③我目前学习数学没有困难；④我期望能学好数学；⑤我对自己能学好数学充满信心）的呈现方式和赋分方式与“数学教师情况”维度相同。用SPSS 26.0对数学教师情况和学生的数学学习情况进行相关分析，先根据调查数据构建数据文件，并计算学生的数学学习情况总分，再选择【分析】→【相关】→【双变量】，将“数学教师情况总分”和“学生的数学学习情况总分”放入【变量】对话框，选择【皮尔逊】，点击【确定】运行，所得结果如表3所示。

由表3可知，数学教师情况与学生的数学学习情况的皮尔逊相关系数约为0.535，可以认为两者中度正线性相关。

四、结语

描述性统计和相关分析是统计分析的基础工作。描述性统计中，对不同条件下变量均值的直观比较是进一步探究不同条件下变量均值之间是否存在显著性差异的前提。相关分析表明了两个变量之间的相关程度，为探究不同变量之间如何相互影响指明了方向，为建立数据模型提供了依据。

（骆仁轩系华中师范大学数学与统计学学院硕士研究生）

［专栏文章系教育部人文社会科学研究规划基金项目“中小学核心素养测评的模型建构与实证研究（19YJA880012）”、中央高校基本科研业务费项目“新高考分省市命题分学科质量评价指标体系研究（CCNUTEI2021-13）”的成果］

责任编辑  刘佳