核心素养下“一课一题”初中几何复习课深度教学策略研究

李美兰

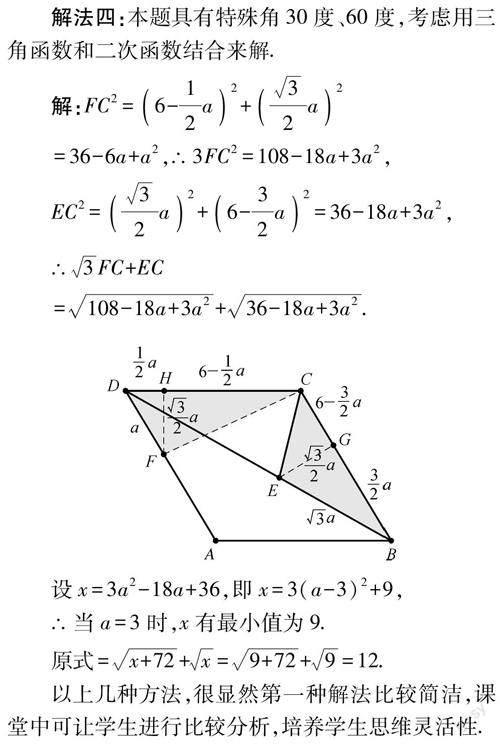
摘 要：深度教学是课程改革发展的必然趋势，为课程改革深入推进提出了新的教育理念和导向.“深度教学”和“深度学习”都离不开知识这一核心载体，并且要促进知识向核心素养转化；“深度教学”是对知识的追问、对学习的追问；教学只有建立在“充分的知识广度”“充分的知识深度”和“充分的知识关联度”的基础上，才能让学生真正获得知识的发展价值.

关键词：深度教学；思维；核心素养

本文着重研究几何综合题的深度教学，挖掘知识内涵的丰富价值，通过科学设置问题引导学生思考，把解题的关键点、重点和难点融入教学提问中，实现知识教学对学生的发展价值.但因为中考压轴题综合性较强，因此教师在教学前应先研究题目，再进行科学改编，防止学生产生思难情绪.例如：

4 深度教学应注重例题变式教学，培养学生思维独创性

不偏离本节课知识这一核心载体，通过各种变式可以让课堂教学建立在“充分的知识广度”“充分的知识深度”和“充分的知识关联度”基础上，使学生思维得到充分锻炼，获得思维发展.例如本节课中，我們可以做以下变式.

变式1：你还可以发现哪些结论？

这样的变式设问让学生不仅仅停留在已经解决的问题上，例如学生会得到最小值时E正好是菱形对角线交点，F是AD中点；若连接AH，则此时的AH=AB等结论.

变式2：若题目改为（无图题）：在正方形ABCD中，AB＝6，连接BD，点E为线段BD的一个动点（不与B、D重合），点F在边AD上，且BE=2DF.求CE+2CF的最小值.

将菱形改为正方形，这样的变式将题目条件更为特殊化.在前面的基础上，学生理解起来会更容易.

变式3：在菱形ABCD中，∠BAD＝120°，AB＝6，连接BD，点E为线段BD的一个动点（不与B、D重合），点F在边AD上，且BE=2DF.求CE+2CF的最小值.

追问：此时E，F是否仍然是中点？（结论：很显然，从图中可知并不是中点）

5 深度教学应注重例题一般性结论的探索，培养学生思维广阔性

例题和几个变式都是系数为定值，系数是相同的，并且都能求出最值，那很自然会有一个新的思维点：是否存在只需要系数相同，都能求最值的一般情况呢？

变式4：在菱形ABCD中，∠BAD＝120°，AB＝a，连接BD，点E为线段BD的一个动点（不与B、D重合），点F在边AD上，且BE=nDF.求CE+nCF的最小值.

解答如右图.

继续追问：那是否任何时候上面最值都成立，系数n的取值范围是什么？

以上变式和追问极大程度拓展了学生思维空间，并引导学生对结论进行提炼.并用该公式检查已求的结果.

变式5：如果点E，F在射线BD、AD上运动，还存在最小值吗？存在最值的条件是什么呢？该变式难度较大，可让尖子生课后研究讨论.

6 深度教学应注重解题策略、关键点、解题思想提炼，培养学生思维概括性

在初中数学课堂中，很多教师对解题后的总结归纳认识是不够的，导致学生大多只注重大量做题，却不重视在解题过程中总结，其实例题的讲解是为了总结步骤、形成策略，题目只是一个载体.就正如榴莲很难开，难开的原因是没有找到一个准确的切开地方，但实际上榴莲有一个位置，只要用刀轻轻一切，再用手一拨，榴莲便切开了，切开它我们用的不是蛮力，也不是乱切，而是有分析、有观察，有方法.相同的几何综合题也是如此，教师在平时教学中应引导学生在解题后进行总结归纳，不要大量地见题讲题.

例如本节课例题讲解后，我们可以引导学生进行总结归纳：

（1） 本节课的解题策略和方法：构造相似三角形，将军饮马模型求最值.

（2） 本题解题关键点和难点是让学生理解为何要构造相似三角形？其目的是什么？运用将军饮马模型的关键点是什么？

结论：

① 构造相似是为了通过相似三角形对应边成比例，将3FC转化为EH.

② 如果两线段系数都为1，那我们可以直接运用将军饮马，或者通过构造全等来进行线段的等量代换.

③ 将军饮马模型运用的关键点是两线段有公共端点，公共端点应是动点.该题有两个动点，因此既可以通过点E连接两线段，也可以通过点F.

（3） 本节课的解题思想是化归转化思想，数形结合思想.

平时教学中我们应该要预留出学生尝试画图时间，鼓励学生遇到类似的问题要勇于画图，敢于画图，老师直接不要就把图形完整呈现，这样学生下次遇到这样的题目还是可能因为不会画图或者不敢画图而影响进一步的思考.

7 几何综合题深度教学应注重解题过程、解题策略、解题思想的板书，培养学生思维的严谨性

数学教学的板书是无声的教学，是完成数学教学任务的重要手段.好的板书不仅有利于学生直观感受解题过程，而且有助于启发学生进行梳理和回顾，有助于培养学生严谨细致的学习习惯.

例如该节课的板书设计是：

8 几何综合题深度教学应注重利用几何画板进行教学，培养学生思维发散性

利用几何画板对教师实现深度地教学设计和学生进行深度地学习起了重要的作用.几何画板有高效、动态、直观等优势，几何综合题难度比较大，图形复杂变化多，借助几何画板，可以实现图形由静态到动态的完整变化，尤其涉及动点问题、需要分类讨论的问题，更是能让学生直观看到图形变化，更有利于学生发现问题、提出问题、解决问题，有助于学生展开深层次地探究和学习.

9 结束语

深度教学是一个潜移默化的过程，培养学生由理性思维逐步过渡到理性精神.数学教育不应停留于帮助学生较好地掌握各种具体的数学知识和技能，而应更加注重促进学生思维的发展，关注学生的专注度、情感态度、思考习惯和学生钻研探索意志力的培养，注重学生核心素养的养成，这些是数学教育的重要目标.

参考文献：

［1］ 鲍建生，黄英金.变式教学研究［J］.数学教学，2003（1）：1112.

［2］ 王千.微时代下的微整合教学模式探讨［J］.教育教学论坛，2014（50）：261262.

［3］ 郑毓信.变式理论的必要发展［J］.中学数学月刊，2006（1）：13.