基于GeoGebra平台,以问题促探究
——以一道解析几何教材习题为例*
张 巧 刘佛莲 王 喆 孔德宏 (云南师范大学 650500)
GeoGebra软件(下称GGB)融合了代数与几何的优势,实现曲线和方程实时交互,是探究解析几何问题的利器.本文从一道解析几何教材习题出发,借助GGB进行数学探究,引导学生经历“发现问题、提出问题、分析问题、解决问题”四个阶段,将圆方程进行推广,归纳得到椭圆、双曲线的第三定义,中心弦性质等结论.本次探究活动既能有效提升学生“四能”,又与新课标“数学建模活动与数学探究活动中,鼓励学生使用信息技术”这一理念相契合.
1 提出问题
人教A版数学选择性必修第一册“2.4圆的方程”有一道课后习题:已知圆的一条直径的端点分别是A(x1,y1),B(x2,y2),求证:此圆的方程是(x-x1)(x-x2)+(y-y1)(y-y2)=0[1].
引导学生观察题目和方程形式,可联想到两向量的数量积,由此打开思路,通过“圆的直径所对圆周角为直角”和“两向量垂直的充要条件”证明得到,此处不作详细分析.
对于数学习题的教学,教师不能让学生思维停留在题目表层,而应适当引导、启发学生思考,鼓励学生积极提出数学问题进行数学探究.基于学生提出的问题,本文对如下几个典型问题展开探究:
问题1已知A(x1,y1),B(x2,y2),点P(x,y)满足(x-x1)(x-x2)+(y-y1)(y-y2)=c(c≠0),则点P的轨迹是什么?
问题2已知A(x1,y1),B(x2,y2),点P(x,y)满足(x-x1)(x-x2)-(y-y1)(y-y2)=0,则点P的轨迹是什么?进一步推广:若点P(x,y)满足(x-x1)(x-x2)-(y-y1)(y-y2)=c(c≠0),则点P的轨迹又是什么?
问题3已知A(x1,y1),B(x2,y2),点P(x,y)满足a(x-x1)(x-x2)+b(y-y1)(y-y2)=0,则点P的轨迹是什么?进一步推广:若点P(x,y)满足a(x-x1)(x-x2)+b(y-y1)(y-y2)=c(c≠0),则点P的轨迹又会是什么?
除以上问题外,学生还提出:交换A,B两点的横纵坐标后,轨迹又是什么?……
2 问题解决
·问题1的探究
猜想由(x-x1)(x-x2)+(y-y1)(y-y2)=c(c≠0)得x2+y2-(x1+x2)x-(y1+y2)y+x1x2+y1y2-c=0,符合圆的一般方程x2+y2+Dx+Ey+F=0形式,猜想轨迹还是圆.
借助GGB展开探究:任意作出A,B两点,创建滑动条c,输入(x-x(A))(x-x(B))+(y-y(A))(y-y(B))=c,拖动滑动条c,观察轨迹.观察到:当c=0时,轨迹是以AB为直径的圆;当c>0时,是直径比AB大的圆;当c<0时,是直径比AB小的圆,但当c一直小到某个值时,轨迹消失(图1).
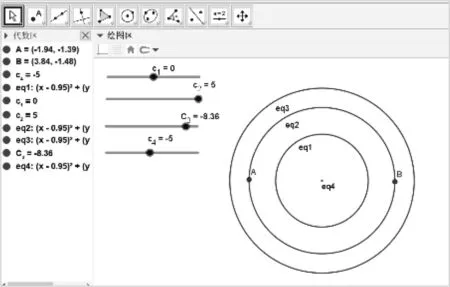
图1
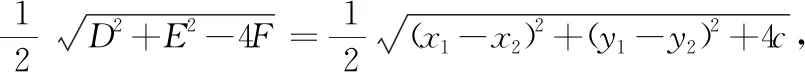

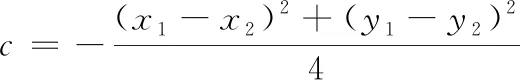
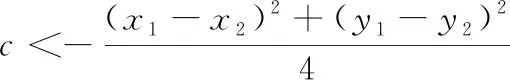
·问题2的探究
猜想将方程展开会得到x2-y2的形式,与双曲线的方程相似,故猜想轨迹为双曲线.
借助GGB展开探究:任意作出A,B两点,创建滑动条c,输入(x-x(A))(x-x(B))-(y-y(A))(y-y(B))=c,改变c的值,观察到:当c=0时,轨迹是以AB为实轴的等轴双曲线;当c>0时,是实轴长比AB大的等轴双曲线;当c<0时,是实轴长比AB小的等轴双曲线,但当c一直小到某个值时,双曲线两支改变方向(图2).
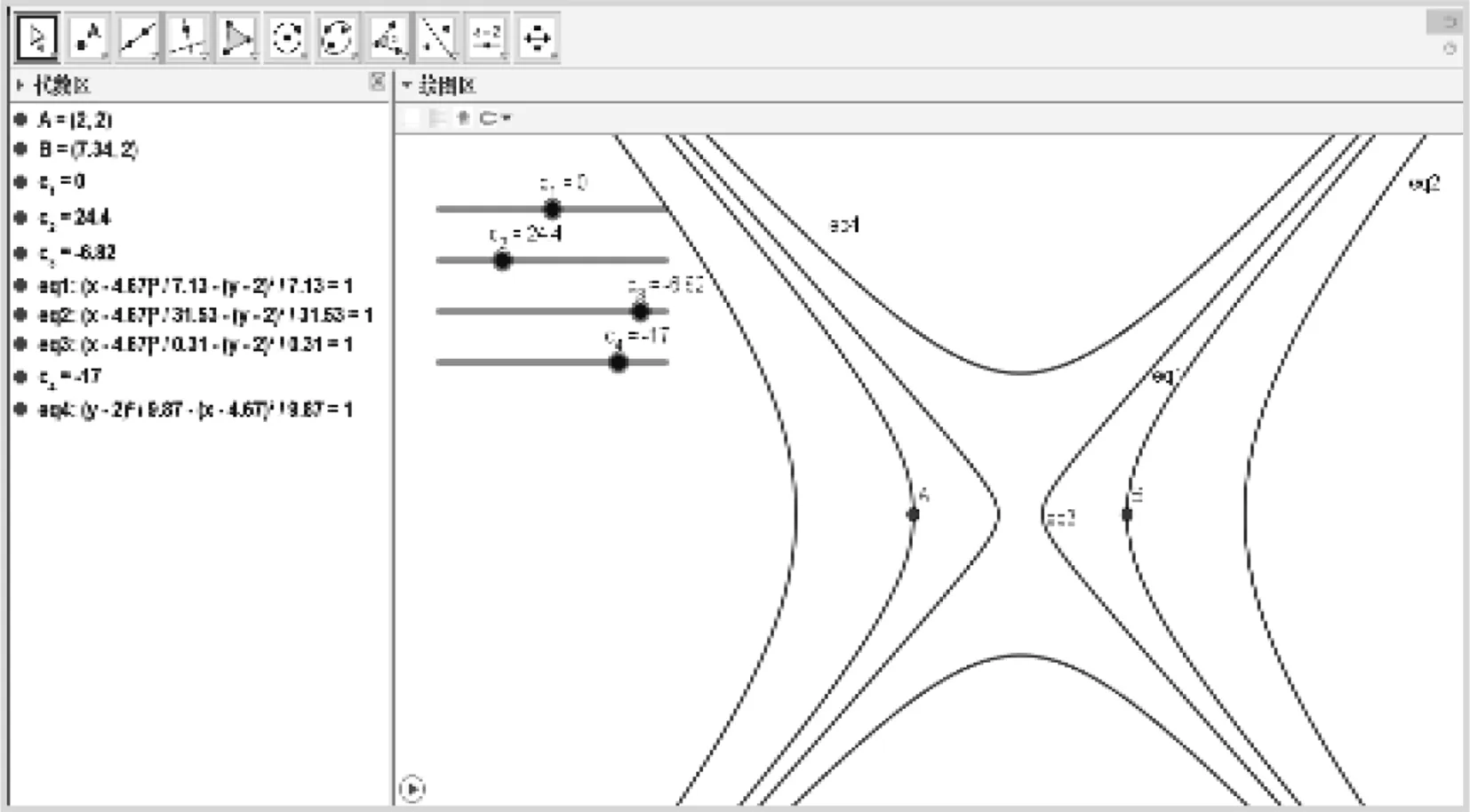
图2
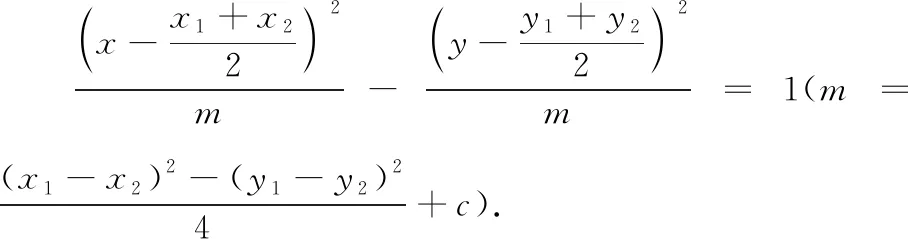
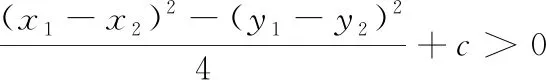
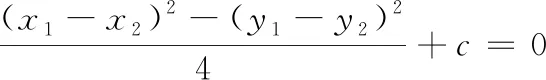
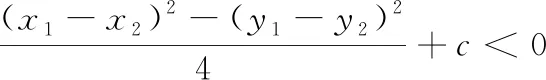
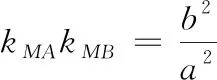
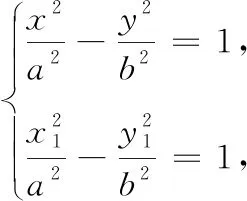
·问题3的探究
猜想将方程左边展开可得到ax2+by2的形式,它既与圆的方程相似又与椭圆方程相似,故猜想轨迹是圆或椭圆.
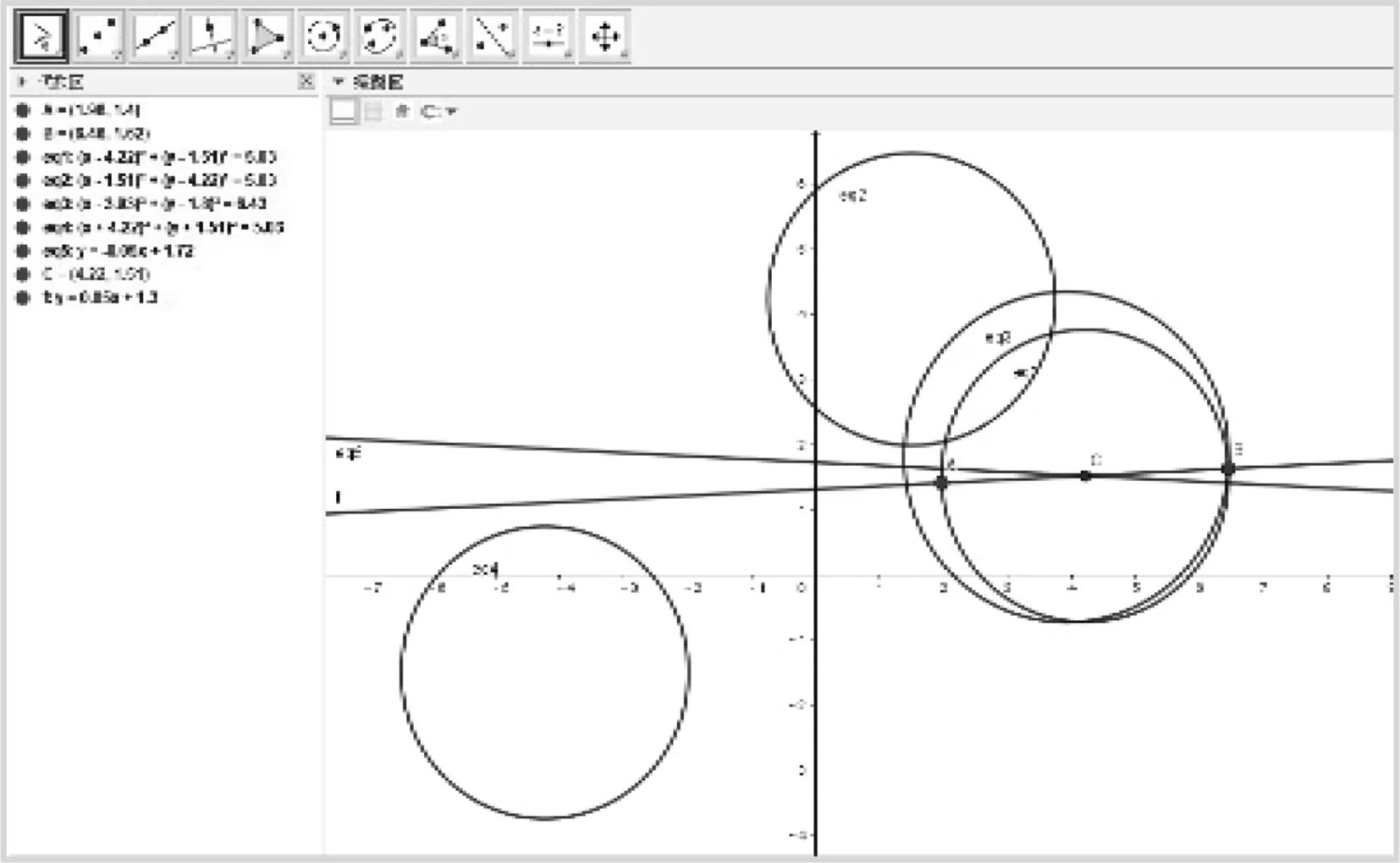
借助GGB展开探究:任意作出A,B两点,创建滑动条a,b,c,输入a(x-x(A))(x-x(B))+b(y-y(A))(y-y(B))=c(a≠0,b≠0),分别改变a,b,c的值来观察轨迹变化情况.观察到当c=0,若a,b异号,则轨迹是以AB为实轴的双曲线,结论与探究2相符;若a,b同号,则轨迹是椭圆;特别地,a=b时轨迹是圆,结论与探究1相符(图3).
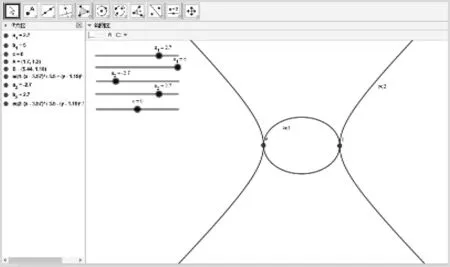
图3
当a,b异号时,轨迹是等轴双曲线.此时,当c>0时,双曲线实轴长小于AB,但当c达到某个值时,双曲线两支改变方向;当c<0时,双曲线实轴长大于AB.
当a,b同号且0 当a,b同号且a>b>0时,轨迹是椭圆.此时,当c>0时,椭圆短轴大于AB;当c<0时,椭圆短轴小于AB;当0>a>b时,将上述结论的短轴变长轴(图4). 图4 探究再进一步,教师可引导学生在此基础上探究斜率之和、差、商为常数时点的轨迹. 此外,学生还可以提出更多问题:(1)(x-y1)(x-y2)+(y-x1)(y-x2)=0(交换点A的横、纵坐标,点B的横、纵坐标);(2)(x-y1)(x-x2)+(y-x1)(y-y2)=0(只交换点A的横、纵坐标);(3)(x+x1)(x+x2)+(y+y1)(y+y2)=0(括号内减变加);(4)(x-x1)(y-y1)-(x-x2)(y-y2)=0(交换前后一个因式且加变减)…… 相应结论:(1)轨迹为圆,且与未交换之前所得的圆关于直线y=x对称;(2)轨迹为圆,且与未交换之前所得的圆有公共点B;(3)轨迹为圆,且与未交换之前所得的圆关于原点对称;(4)轨迹是直线,过直线AB的中点,且与直线AB斜率之和为0(图5). 图5 “以问题促探究”是培养学生钻研数学问题的重要途径,多问几个为什么能激发学生的创新精神,提高数学学习兴趣.近几年的高考试题中,有一些试题是由课本例习题演变而来的.例如: (1)椭圆和双曲线的第三定义.椭圆:平面上任意一动点到两定点的斜率之积为负常数(除-1外)的点的轨迹是椭圆(除两定点).其中两定点是椭圆长轴上的两个端点,并且满足椭圆方程.双曲线:平面上任意一动点到两定点的斜率之积为正常数的点的轨迹是双曲线(除两定点).其中两定点是双曲线实轴上的两个端点,并且满足双曲线方程. (1)以问题促探究,培养学生问题提出能力.问题是深化学生对知识的理解、培养学生的问题提出能力和创新能力的重要武器.引导学生发现和提出有意义的数学问题,猜测合理的数学结论, 提出解决问题的思路和方案,通过自主探索、合作研究、论证数学结论的过程,培养学生的数学思维,发展学生的数学核心素养[2]. (2)教师要注重“用”教材教,而不是“教”教材.新时代的教师应该是教育教学的研究者和反思的实践者,要注重研究教材和教材配套资源的开发与利用.例如,教师应该敢于改编教材习题,引导学生变换题设条件、变换题目结论或增减题中的条件等,多角度、多层次进行探究,使其在“变”中比较,在“变”中感悟不变的规律,提升思维的创造性[3]. (3)信息技术辅助教学,提升直观想象素养.GGB能建立“抽象形式”与“可视内容”之间的直接联系,实现“思维可视化”.基于GGB进行数学探究活动,鼓励学生通过实验、观察、猜想、交流、归纳、验证进行数学探究,揭示数学问题的本质,从而培养学生的数学思维,发展学生的数学核心素养[4].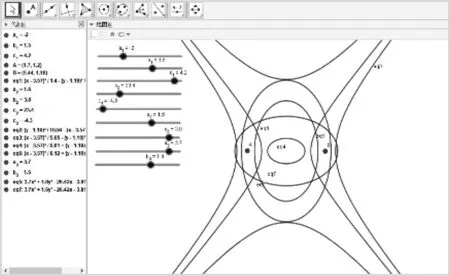
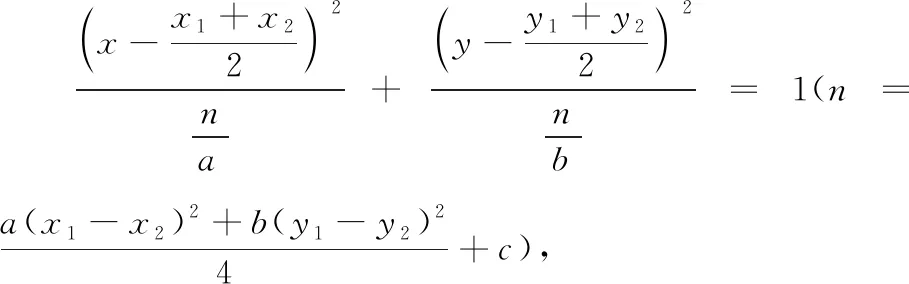
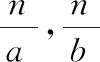
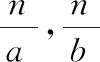
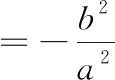
3 进一步探究
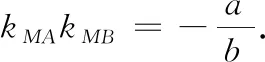
4 应用
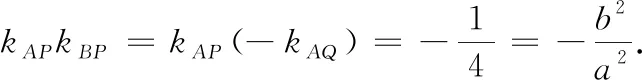
5 结论

6 启示

