高考数学试题中的情境设置及启示
——以2022年高考数学试题为例*
郑蓉蓉 蒋逸卿 唐恒钧 (浙江师范大学教育学院 321004)
1 引言
情境是高考数学命题的三大要素(立意、情境、设问)之一[1],更是承载考查内容、实现考查要求的重要载体.因此,高考试卷中情境化试题的分析研究对把握命题趋势与高考评价方向有重要意义.以下拟对2022年10套高考试题,从情境视角进行分析,在宏观层面总结情境设置的特点,并在微观层面结合具体试题进一步剖析并提出相关的启示与建议.
2 分析框架
《普通高中数学课程标准(2017年版2020年修订)》(以下简称《课标》)将“情境与问题”列为体现数学学科核心素养的首要方面,其中情境主要是指现实情境、数学情境、科学情境,问题是指在情境中提出的数学问题.每种情境又可根据本身的复杂程度分为熟悉、关联、综合三个层次,与数学学业质量水平相对应[2]81.这样的划分,明确了高考数学试题情境的材料来源和载体作用.本文便从情境的三种分类与学业质量维度下情境的三种水平这两方面对2022年高考试题的情境进行分析.
2.1 情境的三种分类
《课标》将情境分为现实情境、数学情境和科学情境三类,分类描述及示例如表1所示.

表1 情境的三种分类框架
2.2 学业质量维度下情境的三种水平
在学业质量维度下,每一类情境可分为熟悉、关联和综合三个层次,分类描述及示例如表2所示.

表2 情境的三种水平框架
3 高考数学卷中情境化试题分布分析
3.1 情境的三种分类
为了更合理地得到情境化试题在整份高考卷中的比重,本文以每道题的分数与总分的比来衡量,用百分数来表示,将结果保留两位小数得到表3.
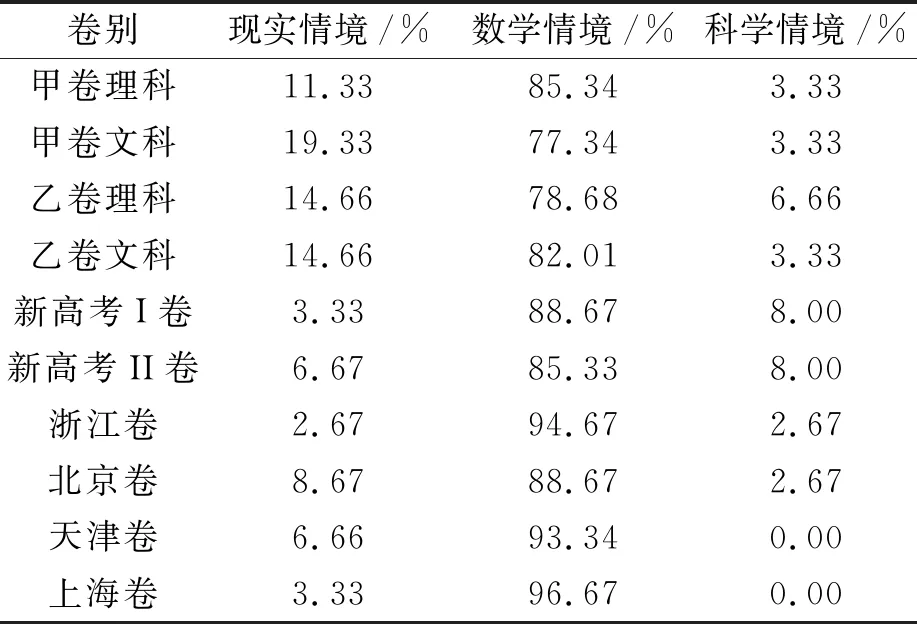
表3 三类情境的卷别:题型分布
表3显示,所有试卷中都是数学情境化试题的比重最大,而且远远超过了其余两种情境.这是因为从广义上说,大部分纯粹的数学问题都是数学情境化试题,这也是由数学的抽象特征所决定的.但数学情境独占全貌的情况已经一去不复返了,2022年数学高考试卷以考查数学情境为主,辅以必要的现实情境与科学情境.学生不仅要掌握数学的基础知识与基本技能,更重要的是理解数学问题的本质,从真实背景中抽离出数学问题,感受数学应用的广泛性,获得数学的基本思想.
另外运用SPSS 25软件进行对应分析,以研究2022年10套高考数学试题与三类情境的考查间的关系.如图1所示,自主命题卷、全国卷以及新高考I卷和II卷在图中大致分属原点周围三个区域且绝大多数距离原点较远,这说明三类高考试卷试题情境设置存在差异,具有比较强的独特性[3].具体地,自主命题卷中浙江卷、上海卷和天津卷与数学情境距离较近且总体远离原点,说明相对于其他卷别,自主命题卷更加注重数学情境化试题的考查,比重更高;同样地,新高考I卷、II卷与科学情境较近且总体距离原点较远,反映了相对于其他卷别,科学情境的设置在新高考I、II卷中的体现更多;相对而言,全国甲、乙文科卷更注重现实情境化试题的考查.
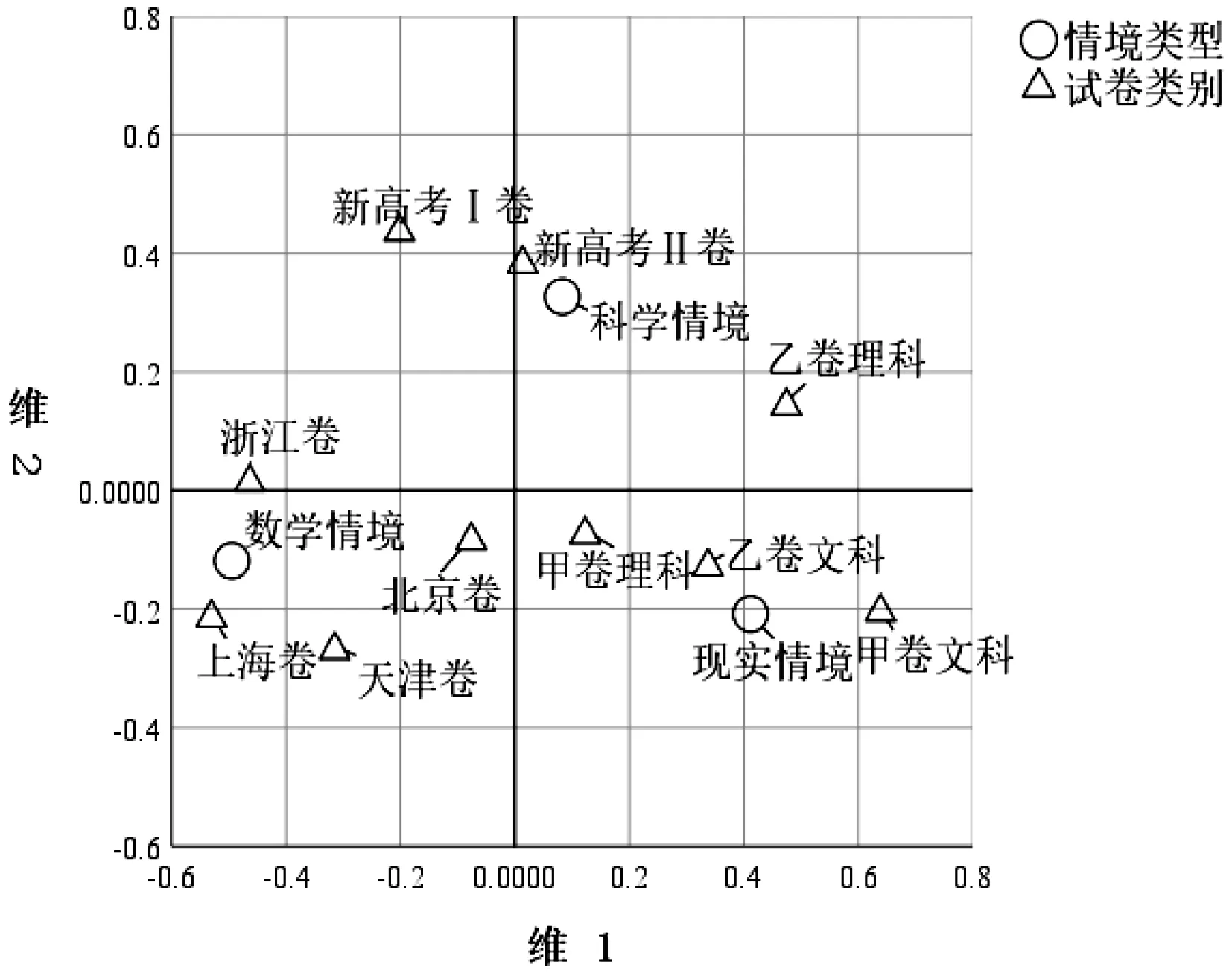
图1 卷别与三类情境对应分析图
3.2 学业质量维度下情境的三种水平
《课标》“学业质量”部分,将“情境”按难度划分为熟悉、关联﹑综合的情境,本文借鉴《课标》的分析框架,将现实情境、数学情境、科学情境按上述三种水平依次划分为九种子情境,并对10套高考卷试题的九种子情境的考查比重进行整理,得出表4.
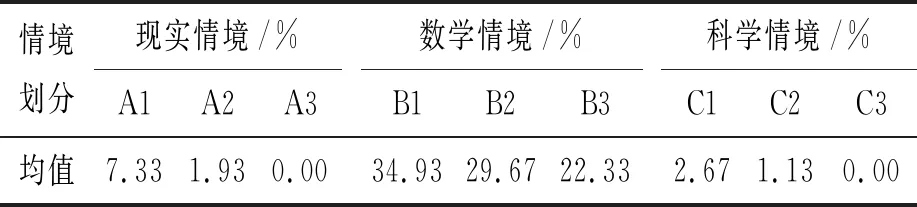
表4 九种子情境总体分布
从整体看,数学情境水平一(B1)在2022年的高考卷中考查的比重最大(34.93%),而现实情境水平三(A3)和科学情境水平三(C3)考查比重最小(0%);试卷以考查熟悉的情境和关联的情境为主(77.66%),并且在每种情境内部都呈现出考查比重随难度水平升高而降低的趋势,这是由学业质量水平二为高考要求决定的.
依据卷别对10套高考卷试题的九种子情境考查情况统计分析(图2),其中天津卷数学情境水平一(B1)比重最大(46.67%),甲卷文科现实情境水平一(A1)比重最大(19.33%),乙卷理科情境种类最丰富(七种).部分试卷情境设置比例相对均衡,如甲卷文科,而另一部分试卷则差异显著,如天津卷.这体现了不同卷别情境设置的关注点存在差异.

图2 九种子情境在10套试题中的分布
4 典型案例分析
综合以上统计分析结果可以发现,2022年数学高考试题的特点是:数学情境比重大且层次丰富、科学情境化试题比重偏低且层次单一、不同卷别的情境关注点存在差异.
4.1 数学情境比重大且层次丰富
例1(2022年北京卷第20题)已知函数f(x)=
exln(1+x).
(1)求曲线y=f(x)在(0,f(0))处的切线方程;
(2)设g(x)=f′(x),讨论g(x)在[0,+∞)上的单调性;
(3)证明:对任意的s,t∈(0,+∞),有f(s+t)>f(s)+f(t).
北京卷第20题属于数学情境化试题,三个小题分别处于数学学业质量水平一(熟悉情境)、水平二(关联情境)、水平三(综合情境)层次,为数学基础与数学能力有差异的学生均提供了发挥空间,更精准地发挥了数学学科考试的选拔区分功能.
小题(1)属于熟悉的数学情境,考查在已知函数解析式的情境下,曲线在某点处的切线方程求法.大部分学生对这题应该都有似曾相识的感觉.该题的求解需要学生在平时解决相似问题的经验中感悟数学的通性通法.因此小题(1)只需根据导数的几何意义,先求出f(x)的导函数,再将点的横坐标代入f′(x)得到在该点处的切线斜率,由点斜式便可求出切线方程.
小题(2)属于关联的数学情境,考查用导数研究较复杂函数的单调性.学生需要掌握常见基本初等函数的导数公式及可导函数四则运算的求导法则,厘清导数与函数单调性之间的逻辑关系,理解其中的数学思想,这样不论遇见多复杂的函数都能够有思路、有信心地往下做.对于本题来说,难点一便是对g(x)进行求导,难点二是判断x∈[0,+∞)时g′(x)的正负情况,需要将g′(x)通分之后才能看出来.
小题(3)属于综合的数学情境,考查导数的综合运用.本题解法不唯一,但是利用数形结合的方法是最简单的.这要求学生具备数形结合的思想,能够借助图形探索解决问题的思路,充分利用小题(2)的结论,由曲线斜率过渡,探索论证途径.由小题(2)可知g(x)在(0,+∞)上是递增的函数,通过求导可得函数F(s)=f(s+t)+f(s)-f(t)在[0,+∞)上单调递增且F(s)>0,故结论成立.
基于以上分析,北京卷第20题的数学情境设置确实层次丰富,这也是2022年高考试题数学情境设置的缩影:数学情境化试题的比重最大且层次丰富,体现了数学高考的科学选拔与全面发展人才的功能.
4.2 科学情境化试题比重偏低层次单一
例2(2022年北京卷第7题)在北京冬奥会上,国家速滑馆“冰丝带”使用高效环保的二氧化碳跨临界直冷制冰技术,为实现绿色冬奥作出了贡献.图3描述了一定条件下二氧化碳所处的状态T与lgP的关系,其中:T表示温度,单位是K;P表示压强,单位是bar.在下列结论中正确的是( ).
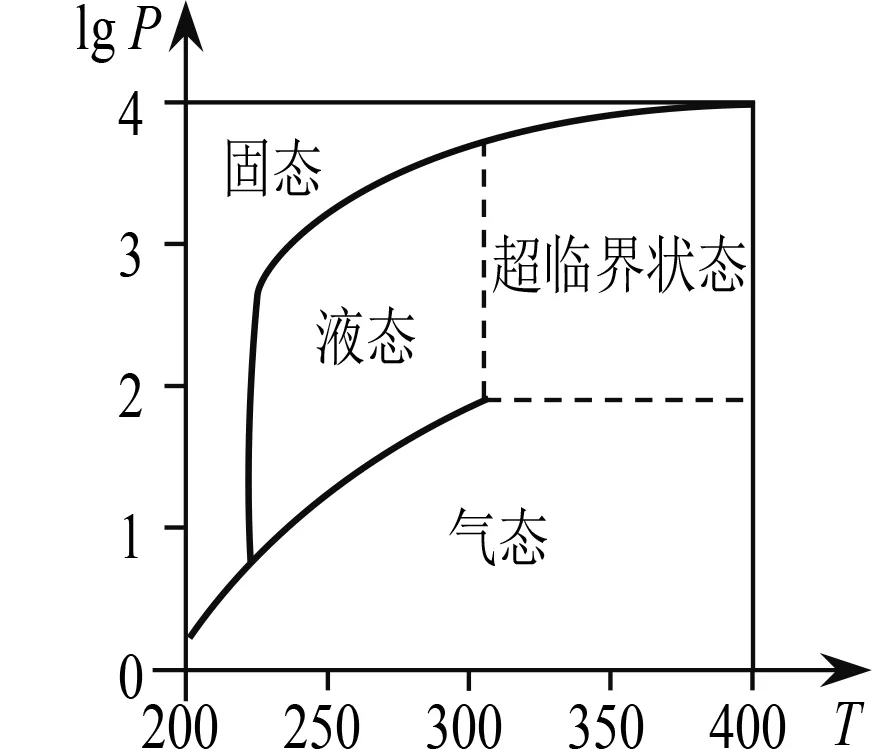
图3
A.当T=220,P=1 026时,二氧化碳处于液态
B.当T=270,P=128时,二氧化碳处于气态
C.当T=300,P=9 987时,二氧化碳处于超临界状态
D.当T=360,P=729时,二氧化碳处于超临界状态
2022年高考卷整体上科学情境化试题比重偏低,且具有情境的复杂水平单一等特点.北京卷第7题以国家速滑馆“冰丝带”绿色环保场馆为背景设置科学情境,考查学生的信息提取能力、数学应用能力和对数数值的估算能力.学生只要能够明确该问题的特征,即坐标位置对应二氧化碳状态,再根据问题特征形成合适的运算思路,依据选项给出的T和P的具体数值,对lgP进行估值后得到相应坐标,对照图表易知二氧化碳所处的状态.因此本题相关知识与问题特征能从情境中直接抽象出来且数学关系单一、运算简单,按复杂程度划分属于熟悉的科学情境.本题虽难度不大,但创设了科学情境将数学与化学联系起来,引导学生发现数学知识在其他学科领域的广泛应用.
4.3 不同地区试卷的情境关注点存在差异
上一节中的图1和图2表明自主命题卷、全国卷以及新高考卷三类高考卷试题情境设置倾向有所差异,反映在自主命题卷更注重数学情境化试题的考查;新高考卷更倾向于科学情境化试题的设置;全国甲、乙文科卷则更关注现实情境化试题.具体表现在:对于同一内容(数列)的考查,三类高考卷设置了不同类型的情境.以下取三道典型试题加以探析.
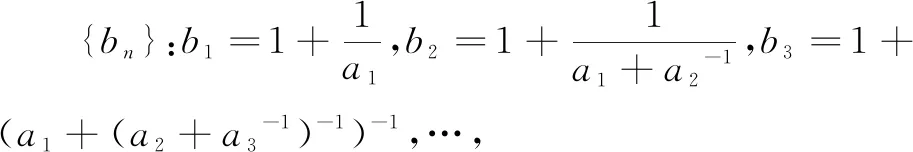
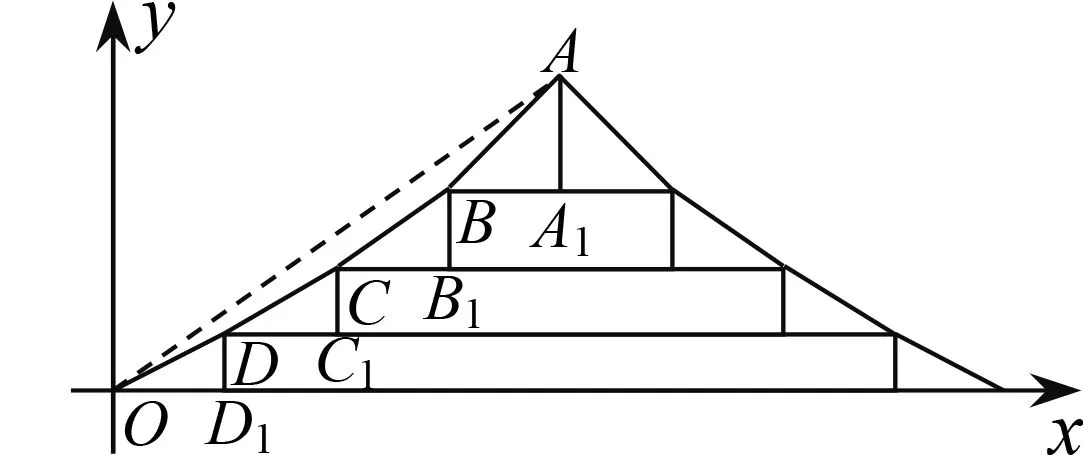
A.b1 C.b6 乙卷理科第4题以嫦娥二号深空探测这一科学活动为情境的载体,设置科学情境.试题里数列递推公式来源于情境中两个绕日周期的比值问题,考查学生数学阅读能力、信息提取能力、综合应用各项知识的能力以及数学运算等核心素养.若能发现ak在题中的任意性,便可取特殊值代入,对复杂的数学问题进行简单、直观的表达,抓住问题的本质,形成解决思路. 图4 A.0.75 B.0.8 C.0.85 D.0.9 新高考II卷第3题依托中国古建筑设置现实情境,考查学生将与学习生活紧密关联的实物抽象为几何图形、建立图形与实物之间的联系、发现图形与数量关系的思维过程,学生进而借助图形探索解决问题的途径,发展直观想象、数学运算等核心素养.本题的关键在于建立等差数列和直线OA斜率间的联系,从而求解得出k3.此题选取中国传统建筑结构为情境载体,可以使等差数列和直线斜率这类理论知识在现实情境中展现生机,贴近现实. 例5(2022年天津卷第18题)设{an}是等差数列,{bn}是等比数列,且a1=b1=a2-b2=a3-b3=1. (1)求{an}与{bn}的通项公式.(2)(3)略. 天津卷第18题第(1)问以数列为背景,通过给出一等差数列和等比数列前三项之间的等量关系构建数学情境.问题的关键是利用等差数列、等比数列的特征进行消元,从而求出公差和公比.这个过程考查学生是否能把握研究对象的数学特征,感悟通性通法的数学原理和其蕴含的数学思想,进而发展学生的数学运算、逻辑推理核心素养. 三道试题考查内容均为数列,整卷中数列题普遍不会超过三道,但不同地区的三类试卷为其设置了不同类型的情境,这在一定程度上反映了三类试卷在情境类型的关注点上具有比较强的独特性. 《课标》指出,高考命题要充分考虑对教学的积极引导作用[2]88.上述研究反映了2022年高考数学试题在情境的类型、层次和卷别倾向上的命题特点,教师应把握命题方向,选择合适的考查载体,以考促学. 2022年高考数学试题均呈现出“数学情境比重大且层次丰富”的特点.数学情境层次的丰富性反映了情境中的问题具有跨度,这需要教师有意识地创设数学情境,用数学问题链组织和驱动教学.时下教学中经常存在教师通过系列问题来推动和引导学生学习的情况,然而教师所提问题之间往往跨度较小且过于直接,限制了学生思考的空间.反观例1,三道小题分属情境由低到高的三个层次,问题之间具有一定的思维跨度,这对当下的问题教学提出了挑战.事实上,数学问题链教学强调通过主干问题驱动学生思考:一方面问题链中问题之间的跨度为学生提供适度思考空间;另一方面为学生的数学思考建构隐性脉络,引向深入[4].基于此,教师首先要充分认识到数学情境是认知活动的信息载体,是发现、提出、分析、解决数学问题的基础;其次,设置具有阶梯性、思维跨度的关键问题,有意识地创设数学情境,使目标问题自然产生,体现以数学思维方法为主线的内在脉络结构.学生在有序解决梯度性问题的过程中主动参与、积极思考,感受基本的数学思维方法,由此对问题产生深度理解[5]. 《课标》提出,要强调数学与生活以及其他学科之间的联系[2]2.数学作为一门基础性学科,在任何学科领域,哪怕是人文社科领域,都有它的身影.数学的交叉和融合是由数学的本质决定的[6].从2022年高考试题中也可以看出,数学已经不再“纯粹”,它能够以各种学科背景为载体考查学生的能力.即使科学情境化试题当前所占比重偏低,对学科交叉融合的重视仍将是体现数学应用价值和时代特征的必然趋势.但是与之相对的,我国数学课程因长期以来强调逻辑性、强调概念定理的深入理解而导致封闭有余而开放不足.因此教师更应该追随新课改的浪潮,更新学科观念,促进学科间的交叉互融,在教学中有意识地设计一些跨学科情境问题,给学生提供自主探索、合作交流的机会,让学生体会用数学的眼光观察世界、用数学的思维思考世界、用数学的语言表达世界. 分析发现,不同卷别的试题情境设置相对而言侧重不同.例3~例5在不同类型的情境中考查同一知识点,这为教学提供了一个参考方向.情境是认知活动的信息载体,设置类型丰富、层次多样的情境,能引领学生从多个角度、多种抽象层次体会数学问题的本质,对同一数学对象的认识和理解也会逐步加深.其次,在不同类型、层次的情境下引导学生采取多种方式表达与交流对于相同数学对象的理解,这有助于学生心智模式的激活与优化,为深度理解提供了可能[6].此外,注重同一对象的多情境认识可以破除一类问题与一种情境间的固化,改变思维定势.例如,高考试题中导数和解析几何的内容往往与数学情境配对,概率统计则常与现实情境结合.这固然受制于知识内容本身的结构特征、应用性程度和考试要求,但教学中需要关注到相关内容的多种情境,如在导数概念教学中创设熟悉的现实情境和关联的科学情境.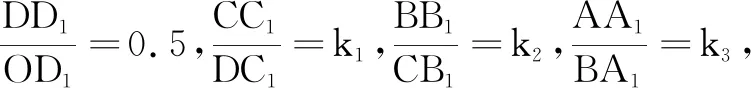
5 启示与建议
5.1 有意识地创设数学情境,用数学问题链驱动教学
5.2 更新学科观念,促进学科间的交叉互融
5.3 注重同一对象的多情境认识,避免问题与情境的固化配对

