2022年北京大学强基数学测试第20题的探究
2023-04-17 09:01黄伟亮广东省佛山市南海区石门中学528248
中学数学月刊 2023年4期
黄伟亮 (广东省佛山市南海区石门中学 528248)
1 试题
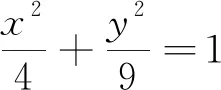
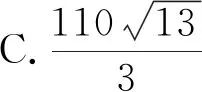
2 解答
这是2022年北京大学强基数学测试的第20题,下面给出一般性的解答.
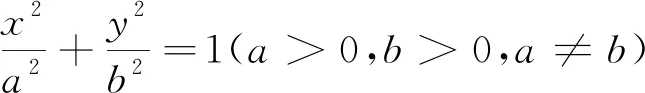
证明由对称性可知,菱形的中心和椭圆的中心重合(图1).
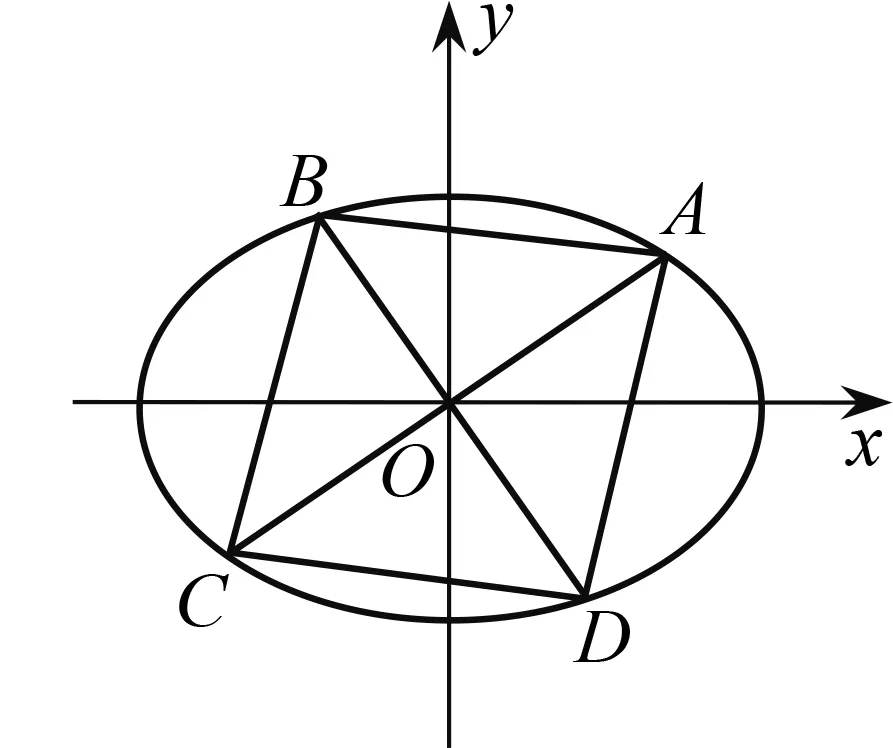
图1
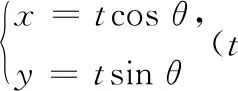
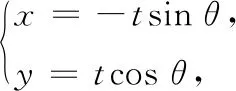
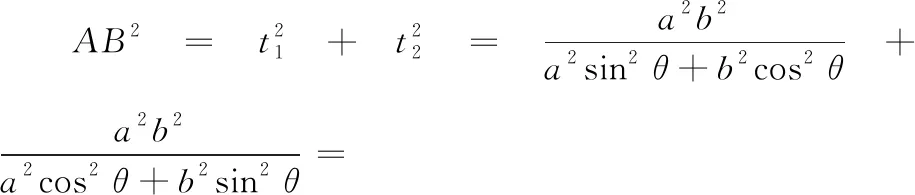
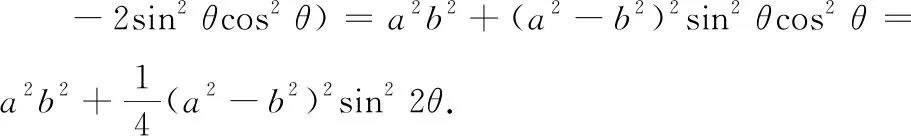

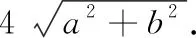

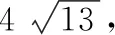
3 探究
这是一道题干精炼、思维丰富的好题,能很好地考查学生综合运用知识的能力.笔者经过研究,将题目进行了以下的探索和推广.
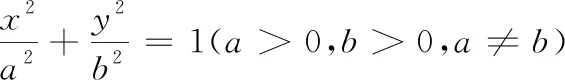
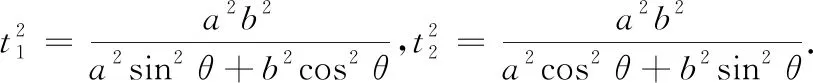

当θ=0时,sin22θ有最小值0,此时m有最小值a2b2,S2有最大值4a2b2,此时菱形面积的最大值为2ab.

我们将椭圆改为双曲线,可得到如下结论:
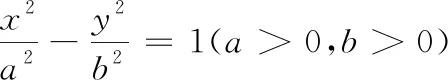
证明由对称性可知,菱形的中心和双曲线的中心重合(图2).
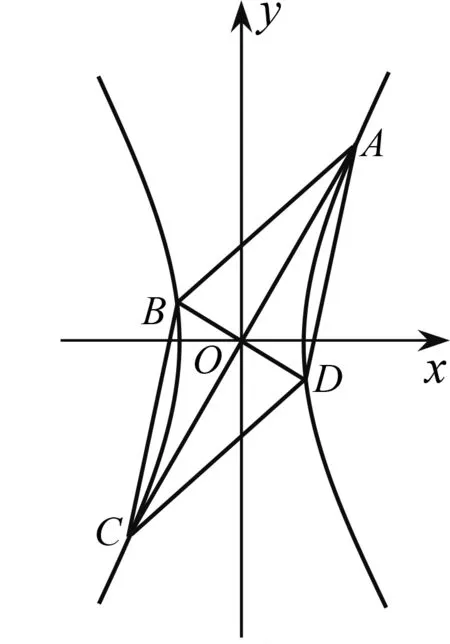
图2
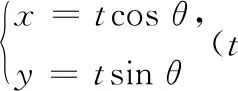
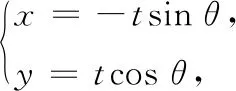

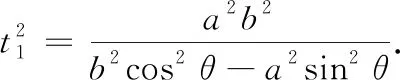
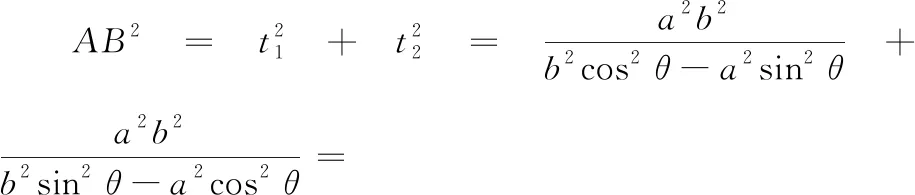
令n=(b2cos2θ-a2sin2θ)(b2sin2θ-a2cos2θ),则n=(a4+b4)sin2θcos2θ-a2b2(sin4θ+cos4θ)=(a4+b4)sin2θcos2θ-a2b2(1-2sin2θcos2θ)=-a2b2+c4sin2θcos2θ=
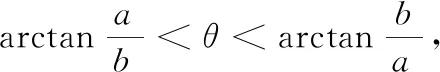
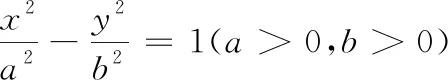
证明 同结论3,可得
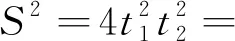
我们将椭圆改为抛物线,可得到如下结论.
结论5抛物线y2=2px(p>0)不存在内接菱形.
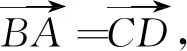
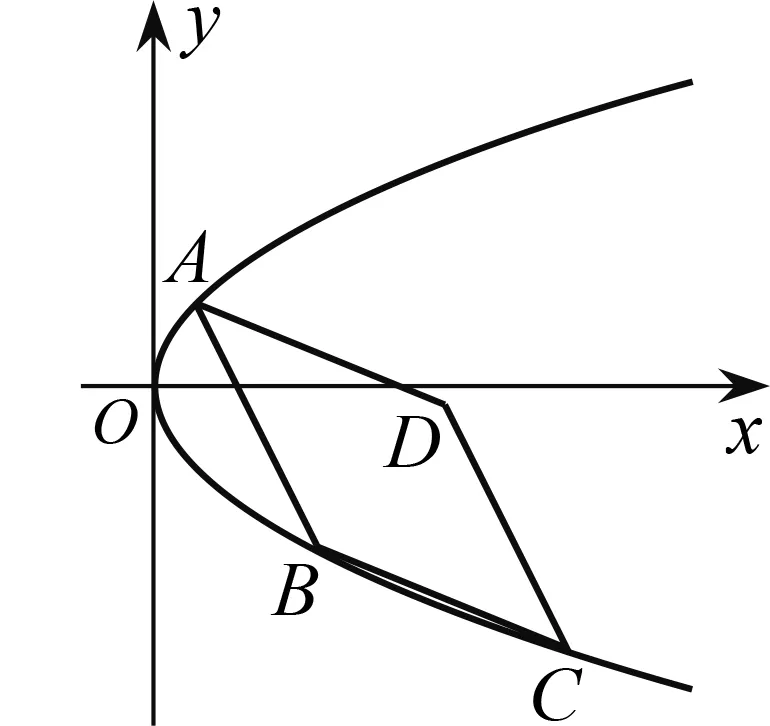
图3
若y2=y1,则x2=x1,点A与点B重合, 不合题意.若y2=y3,则x2=x3,点B与点C重合,不合题意.可见(*)式不能成立,所以假设抛物线y2=2px(p>0)存在内接菱形ABCD是 错误的,即抛物线y2=2px(p>0)不存在内接菱形.
猜你喜欢
数学物理学报(2022年4期)2022-08-22
中学生数理化·中考版(2021年10期)2021-11-22
成都信息工程大学学报(2021年3期)2021-11-22
昆明医科大学学报(2021年8期)2021-08-13
电子制作(2017年10期)2017-04-18
读写算·小学中年级版(2016年5期)2016-05-14
电测与仪表(2015年10期)2015-04-09
电气技术(2013年2期)2013-09-22
资本市场(2008年8期)2008-10-30
意林(2008年12期)2008-05-14

