用换元法探究一类最值问题的解法与推广

程元慧 (安徽省绩溪中学 245300)

对某种复杂的最值问题,如果从题目内部结构出发,通过等价变形,找到变量相等的条件后作换元处理,就能使均值不等式的运用有了用武之地．

例1(《数学通报》2012年第9期数学问题2080题)正数a,b,c满足a+2b+3c≤abc,求5a+22b+c的最小值．

例2(2008年全国高中数学联赛吉林省预赛试题)已知正数a,b,c满足2a+4b+7c≤2abc,求a+b+c的最小值．

按照例1的方法加以分析,同样可以得到下面的简单解法．

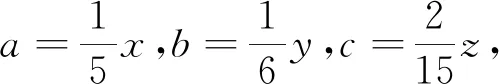
对上述两道例题的解法进一步分析,可将它们作如下推广:

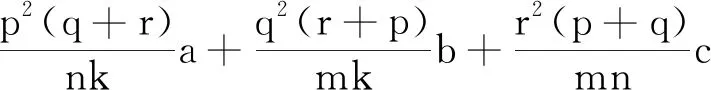
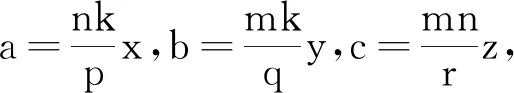
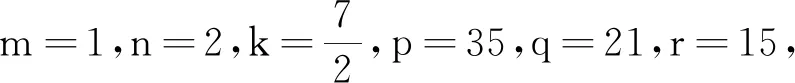
经典的数学问题总是存在着变的学问,或已知条件在变,或所求目标在变,但是不论怎么变,条件和目标之间总隐含着某种神秘的关系,只要在解题时用心观察,仔细思考,就会让这种关系浮出水面,从而打开解题的绿色通道．