基础隐喻数学观下的课堂新认知
张怡文 赵健滢 (南京师范大学教师教育学院 210023)
《普通高中数学课程标准(2017年版)》在课程性质中指出:“数学源于对现实世界的抽象,基于抽象结构,通过符号运算、形式推理、模型构建等,理解和表达现实世界中事物的本质、关系和规律.”[1]数学课程中抽象的内容和表现形式,容易成为学生构建新的数学认知的难点.基础隐喻能以来自生活实物中的经验为来源,依据具体经验与抽象的数学知识之间的某种相似性,建构相关内容的隐喻投射,帮助学生理解抽象的数学概念及数学运算的内涵.本文以基础隐喻为理论基础,创设以生产线、配制酒精溶液为背景的系列化基础隐喻,推动数学知识生活化、形象化发展.
1 概念界定
隐喻,是语言学中的一种修辞手法,以两物之间的相似性进行间接暗示的比喻,从而传递出更富意蕴的内在表达.同时,它也是一种认知现象,用个体对某一实物的经验去理解另一类实物的概念.隐喻认知就是利用在源域中形成的认知经验对靶域进行认识[2].
在隐喻的观点下,数学本质上是一个网络[3].基础隐喻是数学隐喻网络的一个重要组成部分.Lakoff和Núez根据隐喻与数学的关系,认为基础隐喻将数学外的源域(如实物)同数学中的靶域(数学概念或意义)相联系[4].
“定义域是盛着点的容器”是一个经典的基础隐喻的例子,以容器作为数学外的实物源域,去理解数学中抽象的定义域的概念.容器内能放物体是学生已有的认知经验,助力学生构建对定义域内能放点的认识,将生活实践中的具体经验用于认知抽象的数学概念.
2 相关研究
文[4]根据隐喻与数学的关系,区分了基础隐喻和连接隐喻.文[3]从认知心理学基础、数学观和数学教育观三方面剖析数学教育中的隐喻.文[5][6]分别以专家型、熟手型教师作为研究对象,研究数学课堂教学中的隐喻语言.文[7]挖掘隐喻本质,得出具身认知、人际交往、情境场域这三种教师学习经验的隐喻表征路径.文[8]利用具身认知理论,发现隐喻思维有益于对数学抽象内容的理解.
现有研究以思辨研究为主,聚焦在隐喻本质内容,包括结构隐喻、方位隐喻及本体隐喻,鲜少有学者研究隐喻的课堂落实案例.故本文以数学隐喻网络下的基础隐喻为出发点,来设计能真正落到实处的教学案例.
3 教学案例
3.1 求复合函数的解析式
两个函数y=f(u)和u=g(x),如果通过中间变量u,y可以表示成x的函数,那么称这个函数为函数y=f(u)和u=g(x)的复合函数,记作y=f(g(x)).
求复合函数的解析式,其本质是对对应关系的深度理解.在函数概念从初中的“变量说”拓展到高中的“对应说”的过程中,“对应关系”的概念就像“函”字所表示的未知盒子,对于学生来说仍是陌生的.代入法、配凑法和换元法是解决此类问题的常见方法.但是,学生缺乏对“对应关系”的深度理解,在解题过程中往往面临知其然而不知其所以然的窘境.因此,本文以基础隐喻为理论支撑,创造性地引入原料、生产线、产品等一系列基础隐喻,借助生活中的生产线问题形象化地阐释计算中的数学内涵(表1).

表1 生产线问题的基础隐喻
例1设函数f(x)=2x-1,则函数f(x+1)=,f(f(x))=.
分析教师引导学生将f想象成一条生产线,原料A在生产线f的作用下变成原来的两倍减一,得到一个2A-1的产品.当学生对以生产线为源域的基础隐喻有了初步了解,教师再次引导学生考虑原料为x,x+1,f(x)的情况.
例2设函数f(x)满足f(x+1)=2x+1,则函数f(x)=.
分析教师通过基础隐喻启发学生转化问题,将抽象的求解对应关系的问题转化为形象的生产线对原料x+1的操作过程.通过配凑法,将原式改写为f(x+1)=2(x+1)-1,使学生能直观地看出生产线f的操作过程是将原料变成了原来的两倍减1,那么以x为原料得到的产品即2x-1.
3.2 求复合函数的定义域
学生初学复合函数时容易混淆定义域的范围与内函数的范围,而教师在讲解时往往难以用形象的语言解释解法的缘由.文[9]以映射、管制的语言解释解法过程,但这样的解释对学生而言仍然略显抽象.为了更形象化地解释这一问题,本文创造性地引入预加工过程、原料、原料规格、生产线、产品等一系列基础隐喻,以原料规格作为问题突破口,帮助学生理解求复合函数定义域的整个计算过程(表2).

表2 原料规格问题的基础隐喻
例3已知函数f(x-1)的定义域为[-2,3],求函数f(2x+1)的定义域.
分析教师首先需要提醒学生,定义域[-2,3]指的是函数f(x-1)中x的范围,引导学生借助整体思想将圆括号中的内函数x-1视作原料,其范围即原料的规格.原料规格这一基础隐喻便是连接前后两个定义域范围的桥梁.解题过程分为四步:
第一步 预加工过程,即从x的范围得到x-1的范围为[-3,2].
第二步 明确原料规格,原料规格即 [-3,2].
第三步 确定新原料并列式,2x+1作为原料需要符合原料规格,即-3≤2x+1≤2.
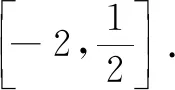
3.3 平面向量基本定理
在学习平面向量基本定理之前,学生已学习过共线向量基本定理,初步体验了用“少”来表示“多”的思想.但是,由“一维直线”上升到“二维平面”,对于学生来说是一个思维的跨越.
在平面向量基本定理的学习中,对于基底的理解,学生可能会存在困惑.实际上,基底暗含了数学中基本量的思想.“基本量思想是数学思想,我们在遇到一串量的时候,首先想到能不能从中选出几个量作为基本量,而其余的量都可以用基本量来表示或计算.”[10]
基本量的思想在高中数学乃至高等数学中都有着重要的作用,本节课为学生领悟这个思想提供了一个宝贵机会,教学中应抓住并利用好这个机会.对于基本量的教学,本文引入以生活中的“配制酒精溶液”问题为源域的基础隐喻来帮助学生理解基本量的价值(表3).

表3 配制酒精溶液问题的基础隐喻
例4引入基本量的教学情境.
在生物实验室中,要用到不同含量的酒精.例如在鉴定脂肪的实验中,要用体积分数为50%的酒精洗去浮色;灭菌消毒需要体积分数为75%的酒精;观察植物细胞的有丝分裂时,需要体积分数为95%的酒精.但是,无论体积分数是多少的酒精,都可以由“乙醇(可以看作是100%的酒精)”和“水(可以看作是0%的酒精)”通过不同的比例混合后得到.“乙醇”和“水”就是酒精全体中的两个基本量,可以由它们来产生任意含量的酒精.
教师引出了基本量后,需要引导学生思考:是否能用75%的酒精和水得到任意含量的酒精?答案是否定的,如95%的酒精就无法得到.因此对于基本量的选择,是需要符合一定要求的.直观来看,75%的酒精中含有水,因此75%的酒精和水之间是有交叉的,不是互不相关的.
类比于生活中的任意含量的酒精,在数学中,平面上有无数个向量,教师可启发学生思考:能不能从中选基本量进而生成任意的向量?
借助共线向量基本定理,即“位于同一直线上的向量可以由位于这条直线上的一个非零向量表示”,教师提示学生将“一个非零向量”视作基本量,通过数乘运算得到这条直线上的任意向量.由直线到平面,学生便自然猜想到平面上基本量的个数应为2.
那么,怎样的两个向量能表示出平面上所有的向量呢?教师进一步启发学生根据前面例子中“乙醇”和“水”两个基本量互不相关的特点,猜想出作为基本量的两个向量之间需要满足的关系.
4 教学启示
数学具有抽象性是普遍的共识.对学生而言,由于数学抽象能力还未达到一定高度,在初学数学知识时容易遇到认知壁垒.教学过程中的基础隐喻能作为他们认知抽象的数学概念的“脚手架”,帮助打破认知壁垒,让抽象的概念在具体经验的基础上得以生长.
以生活化的生产线问题创设的基础隐喻,能帮助学生克服学习“对应关系”概念的认知困难,引导学生在生活经验的背景下去理解数学概念;以配制酒精溶液为背景的基础隐喻,更能契合平面的二维特征,帮助学生理解找基本量的目的及基本量的特点.
基础隐喻,以生活中熟悉的实物为切入点,能增进学生对数学概念的理解,为教师在教学过程中突破数学抽象性这一教学难点提供了思路.基础隐喻在真实课堂中的运用,是帮助学生更好地发展数学认知的一次尝试.以具体的经验来源作为源域,拉近了抽象的数学概念与现实生活之间的距离.

