顺应“三新”趋势探索变式——数学变式征集活动解析几何专题试题选登

【精选变式题组】

【母题1】设A1,A2是圆的一条直径的两个端点,P1P2是与A1A2垂直的弦,则直线A1P1与A2P2的交点P的轨迹方程为________.

【变式1】(方法变式)将母题题设中的“圆”换为“椭圆”

设A1,A2是椭圆长轴的两个端点,P1,P2为与A1A2垂直的直线与椭圆的两个交点,则直线A1P1与A2P2的交点P的轨迹方程为________.

【变式2】(方法变式)将母题题设中的“圆”换为“双曲线”

【变式3】(方法变式)将题设的“圆”换为“抛物线”,以抛物线y2=2px(p>0)为例

已知抛物线y2=2px(p>0)的焦点为F,准线与x轴的交点为C,P1,P2为与x轴垂直的直线与抛物线的两个交点,则直线P1F与P2C的交点P的轨迹方程为________.

【母题2】已知圆C:x2+(y-2)2=4,过坐标原点作圆C的弦OM,求OM中点P的轨迹方程.

【变式1】(知识变式)特殊位置的点O(0,0)变为非特殊位置A(2,3)

已知圆C:(x-1)2+(y-1)2=9,过点A(2,3)作圆C的任意弦,则这些弦的中点P的轨迹方程为________.

【变式2】(方法变式)直接法求轨迹方程

( )

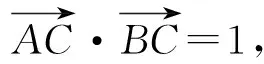
A.圆 B.椭圆

C.抛物线 D.直线

【变式3】(综合变式)曲线方程由圆变为椭圆

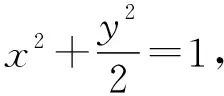
【变式1】(知识变式)由距离之差为常数变为距离之和为常数

已知F1,F2是定点,且|F1F2|=8,若动点M满足|MF1|+|MF2|=8,则动点M的轨迹是

( )

A.椭圆 B.直线

C.圆 D.线段

【变式2】(方法变式)由距离之差为常数变为距离之和为常数并融入三角形

已知在△ABC中,B(-6,0),C(6,0).若三角形ABC的两边AB和AC上的中线CE与BD之和为30,则三角形重心G的轨迹方程为________.

【变式3】(综合变式)由距离之差为常数变为距离之和为常数并融入分类讨论的思想

( )

A.椭圆 B.线段

C.不存在 D.椭圆或线段

【母题详解及答案】

【母题1】【解题策略】本题考查利用交轨法求轨迹方法,运用数形结合等方法来解决,落实基础性的考查.

【解题思路】【解法1】点拨:建立适当的平面直角坐标系,确定圆的方程,然后设出点的坐标,直线A1P1与A2P2的方程,利用交轨法求得点P的轨迹方程.

如图,以圆心为坐标原点O,以A1A2所在直线为x轴,建立平面直角坐标系xOy.

设A1(-r,0),A2(r,0)(r>0),则圆的方程为x2+y2=r2.

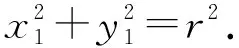
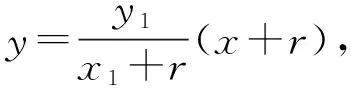
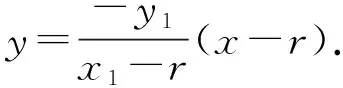
整理得x2-y2=r2,即为点P的轨迹方程,轨迹为等轴双曲线.

【解法2】点拨:解法1给出的是常见的求解轨迹的方法——交轨法,但并不是最佳解法.注意到解法1中利用条件P1,P2关于x轴对称,和P1,P2在圆上坐标满足x12+y12=r2,我们还可以将两个条件合二为一利用圆的参数方程表示P1,P2.

设P(x,y),P1(rcosα,rsinα),则P2(rcosα,-rsinα),

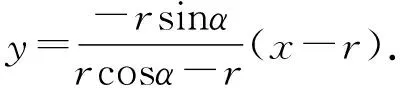
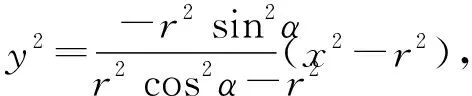
整理得x2-y2=r2,即为点P的轨迹方程,轨迹为等轴双曲线.

(作者单位 姓名:贵州省贵阳市第一中学 李 寒)

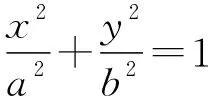
【变式3】y2=2px

(作者单位 姓名:山东泰安英雄山中学 尹承利)

【母题2】【解题策略】本题可分别采用直接法、定义法、相关点法求解.

【解题思路】【解法1】(直接法)设P(x,y),C(0,2),依题意知|OP|2+|CP|2=|OC|2,即x2+y2+x2+(y-2)2=4,

整理得x2+y2-2y=0,即x2+(y-1)2=1,

经检验,坐标原点不符合题意,否则不存在弦OM,

∴点P的轨迹方程为x2+(y-1)2=1(y≠0).

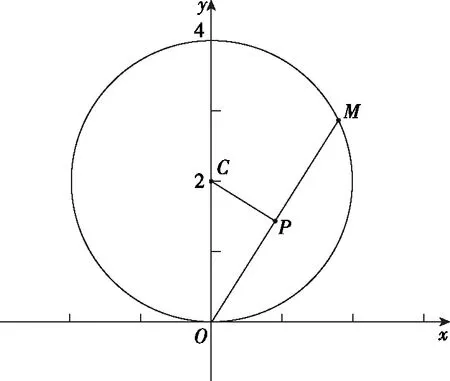
【解法2】(定义法)如图,作OC的中点为N,N(0,1),则NP为△OCM的中位线,

∴点P的轨迹是圆,方程为x2+(y-1)2=1,

经检验,坐标原点不符合题意,否则不存在弦OM,

∴点P的轨迹方程为x2+(y-1)2=1(y≠0).

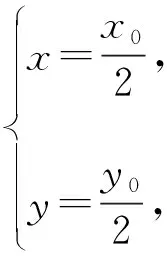
整理得x2+y2-2y=0,即x2+(y-1)2=1,

经检验,坐标原点不符合题意,否则不存在弦OM,

∴点P的轨迹方程为x2+(y-1)2=1(y≠0).

(作者单位 姓名:曲靖经开区第一中学 林之鸿)

(作者单位 姓名:河北定州中学 赵伟娜)

【变式2】A

(作者单位 姓名:曲靖经开区第一中学 林之鸿)

【变式3】2x2+y2-2ax-by=0

(作者单位 姓名:河北定州中学 赵伟娜)

【母题3】【解题策略】本题既可用坐标法求解,也可以用双曲线的定义求解.相应解题步骤的思维导图如下:

【解题思路】【解法1】点拨:坐标(直接)法求解

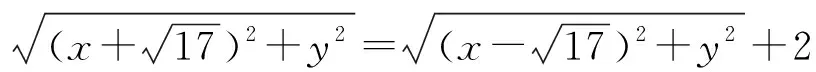
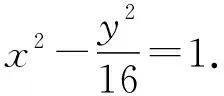
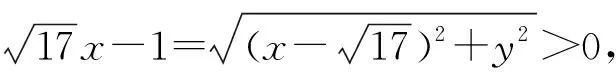
【解法2】点拨:定义法求解

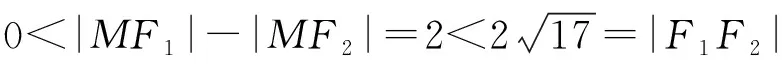
【变式1】D

【变式3】D