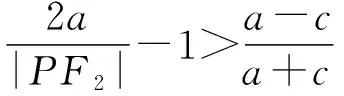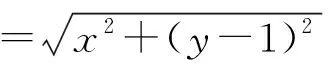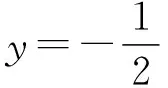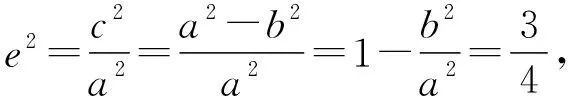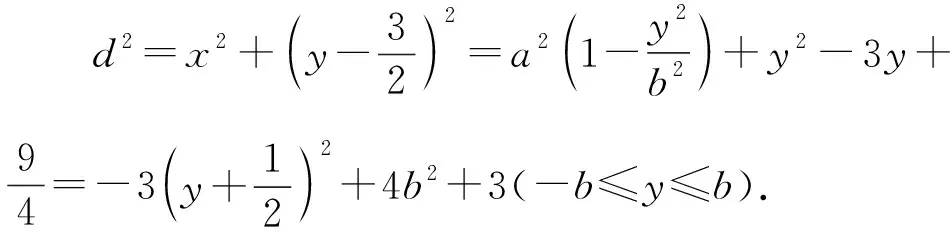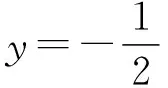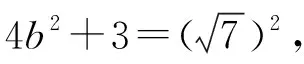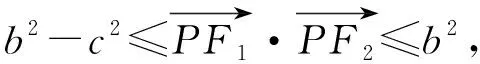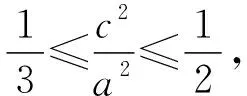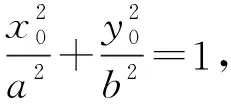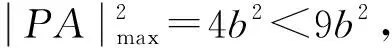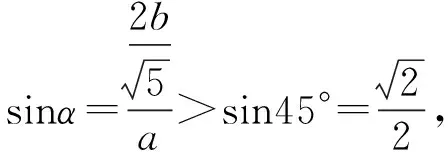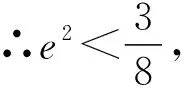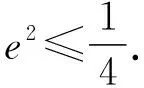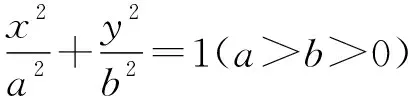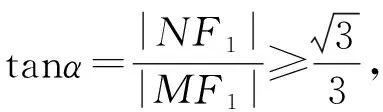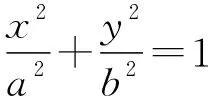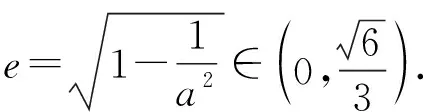突出理性思维 培养关键能力
——椭圆几何性质中的范围问题
秦 俭 林 方
(1.湖北省武汉市华中师大一附中;2.湖北省武汉市湖北大学附属中学)
题型一:与椭圆边界性质有关的范围问题
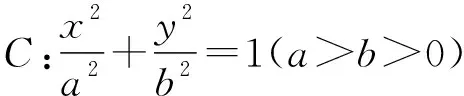


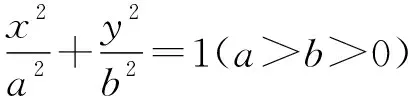
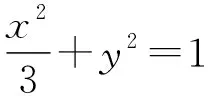


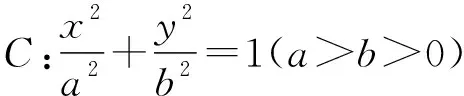
题型二:与椭圆几何性质有关的范围问题
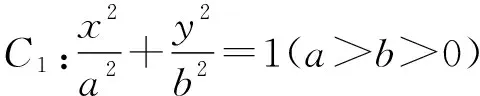


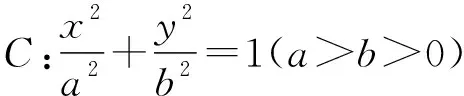

【答案与详解】
【题1】设P(x0,y0),


因为-b≤y0≤b,

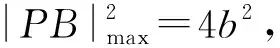
即|PB|max=2b,符合题意,
由b2≥c2可得a2≥2c2,
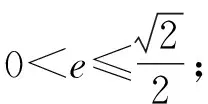


显然该不等式不成立,故选C.


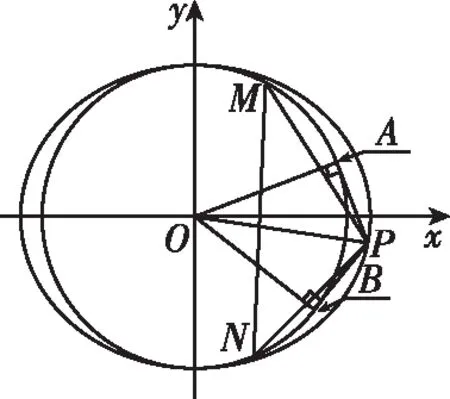
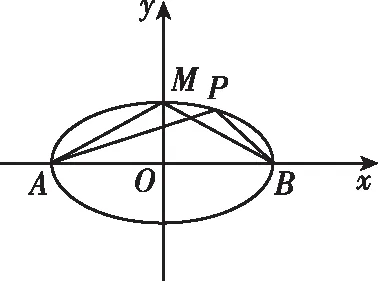
由椭圆的几何性质,知a-c<|PF2| 即e2+2e-1>0且e2+1>0, 【题3】由已知得到P(0,1), 设Q(x,y)是椭圆上的任意一点, 所以x2=3(1-y2), 又因为-1≤y≤1, 【题4】依题意可设椭圆的标准方程为 设椭圆上的点(x,y)到点P的距离为d, 则当y=-b时,d2有最大值, 从而d有最大值, 解得b2=1,所以a2=4, 【题5】设点P(x,y), 因为0≤x2≤a2, 即b2-c2≤c2≤b2, 【题6】易知A(0,b),设P(x0,y0), 若在C上存在点P,使得|PA|=3b, 则等价于|PA|max≥3b, 则a4+9c4-9a2c2≥0, 整理得9e4-9e2+1≥0, 【题7】由题意,如图, 若在椭圆C1上不存在点P, 使得由点P所作的圆C2的两条切线互相垂直, 则只需∠APB>90°, 等价于∠APB的最小值大于90°, 当点P位于C1的长轴端点时,∠APB的值最小, 即设∠APO=α>45°, 因为a2=b2+c2,则3a2>8c2, 【题8】连接OP, 当P不为椭圆的上、下顶点时, 设直线PA,PB分别与圆O切于点A,B,∠OPA=α, ∵存在M,N使得∠MPN=120°, ∴∠APB≥120°,即α≥60°. 又α<90°,∴sinα≥sin60°. 又P是C上任意一点, 证明:设P(x0,y0),半焦距为c, 由椭圆的对称性,不妨设y0>0,x0≥0, 此时tan∠APB<0,故∠APB为钝角, 又当y0最大,即P为短轴的上顶点时, tan∠APB最大,即∠APB最大. 当0 设上顶点为M,则∠AMB≥120°, 当m>3时,此时焦点在y轴上, 设右顶点为N,则∠ANB≥120°, 综上所述,m的取值范围是(0,1]∪[9,+∞). 【题10】由椭圆的对称性知|NF1|=|MF2|, 且|MF2|+|MF1|=2a. 因为|MN|=|F1F2|, 所以四边形MF1NF2为矩形, 设∠NMF1=α, 因为2a=|MF2|+|MF1|=2c(sinα+cosα), 证明:设点P(x0,y0),当切线的斜率存在时, 过点P作椭圆的切线方程为y=k(x-x0)+y0, 令m=y0-kx0, 与椭圆方程联立消y整理得(1+a2k2)x2+2kma2x+a2(m2-1)=0, 当切线的斜率不存在时,P也在圆x2+y2=a2+1上. 因为圆x2+y2=a2+1上任意一点向椭圆C所引的两条切线互相垂直, 所以当直线3x+4y-10=0与圆x2+y2=a2+1相离时,∠APB恒为锐角, 解得1