对一道高档导数题求解的心路历程
王安寓
(江苏省南京市六合区实验高级中学)
在高三复习过程中,我们师生撒遍各市模考题.2023届如皋期初调研试卷第16题是一道含lnx,ex的导数压轴题,看我抽剑战天涯,运用文韬武略战而胜之.
一、题目呈现及分析
【题目1】(2023·如皋期初·16)已知关于x的不等式aeax≥lnx对任意x≥1恒成立,则实数a的取值范围是________.
分析:题目1将自然对数、指数函数、参数巧妙揉合在一道试题中,命题设计新颖,条件简洁,目标明确,题目短小精悍而又内蕴丰富,是一道考查能力的高档题目.
题目1的条件有二:①x≥1是不等式成立的大前提,相当于函数的定义域,可考虑边界值和某些特殊值(数感);②关于x的不等式aeax≥lnx是题设主干,既含有两个变量x,a(x是主元,a是参数),又含有lnx,ex,且参数a既嵌入ex的指数中又作为其倍数,结构奇异,不易展开联想(虽然有y=lnx与y=ex互为反函数,但很难应用上).
题目1的待求简单:参数a的取值范围.这是研究不等式aeax≥lnx对任意x≥1恒成立时的充要条件.
如何处理不等式aeax≥lnx是整个试题求解的难点.联想常用处理不等式恒成立的方法,能否找到突破口?常用恒成立求参问题的一个好方法是分离参数法,但题目1中的参数a既嵌入ex的指数中又作为其倍数,难以分离;常用恒成立求参问题的另一个方法是构造一个合适的函数,研究函数的最值,由最值构造不等式,通过解不等式求解参数的取值范围.而题目1中的函数aeax,lnx该如何组合变形,才能便于研究函数的单调性求最值?粗略观察,构造新函数很困难.
两种常用方法都陷入幽谷.
二、题目1求解的心路历程
笔者再读题目1,盯着它,审视它,该从何处破解?
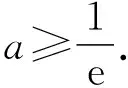
解法一(数感):显然当a=0时,
不等式aeax≥lnx不恒成立,∴a≠0.
令x=1,得aea≥ln1=0,∴a>0.
令x=e,得aeae≥lne=1,
两边取自然对数得lna+ea≥0,
设f(a)=lna+ea,a>0,
显然f(a)在(0,+∞)上单调递增,
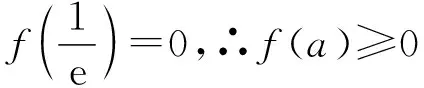
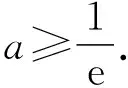
评注:数感是指对数据的敏感性,借助对数的敏感性取数检验或判断,是数感的一种合理应用,但是数感毕竟是特殊值检验,并不能保证答案的准确性,只能说,由特殊值所得结果将待求参数范围大大缩小了.
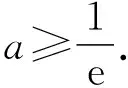
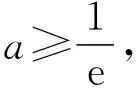
重新读题,重新审视它,重新思考.冷冰冰的“数”背后还有直观的“形”.从形上看,y1=lnx与y=ex相隔银河而望,银河的边界是直线y=x+1与直线y=x-1,如图1,而y2=aeax是由y=ex的图形伸缩变换而得,仍然先由特殊值缩小a的取值范围得a>0,再考虑a对y2图象的影响.

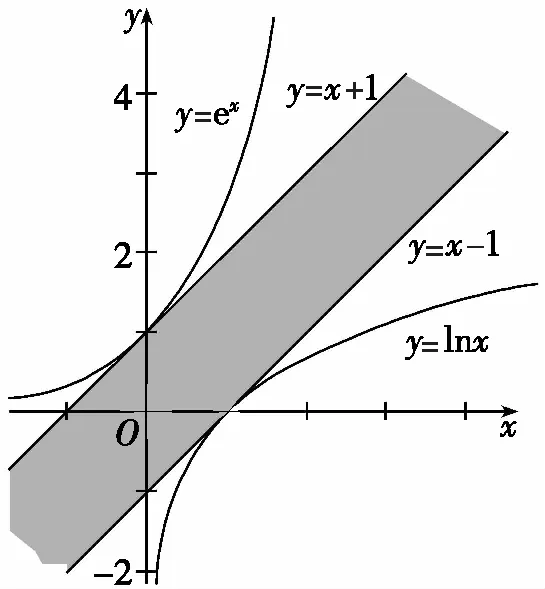
图1
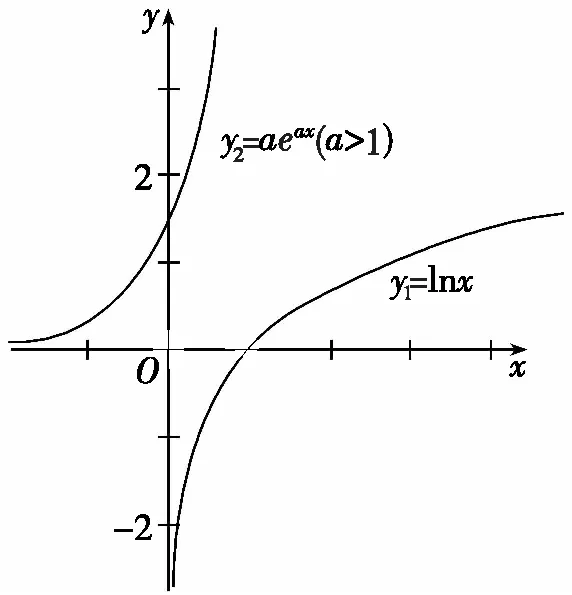
图2

图3

解法二(相切法):显然当a=0时,
不等式aeax≥lnx不恒成立,∴a≠0.
令x=1,得aea≥ln1=0,∴a>0.
当a=a0时,设y1=lnx与y2=a0eax相切于点P(x0,y0),x≥1,
则y0=a0ea0x0=lnx0,

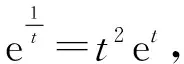

显然F(t)在(0,+∞)上单调递增,
且F(1)=0,∴F(t)=0的解有且只有t=1,
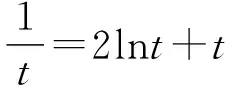
随着a的增大,y2=aeax逐渐远离y1=lnx,
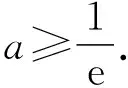
评注:解法二是动态分析静态求解,先由a的几何意义(伸缩)观察图形,得到临界位置—相切,再由“切”通过导数构造方程组,然后消元、取对数、构造函数解方程,最后由a的几何意义得到a的范围.此解法思维量大,运算繁琐.
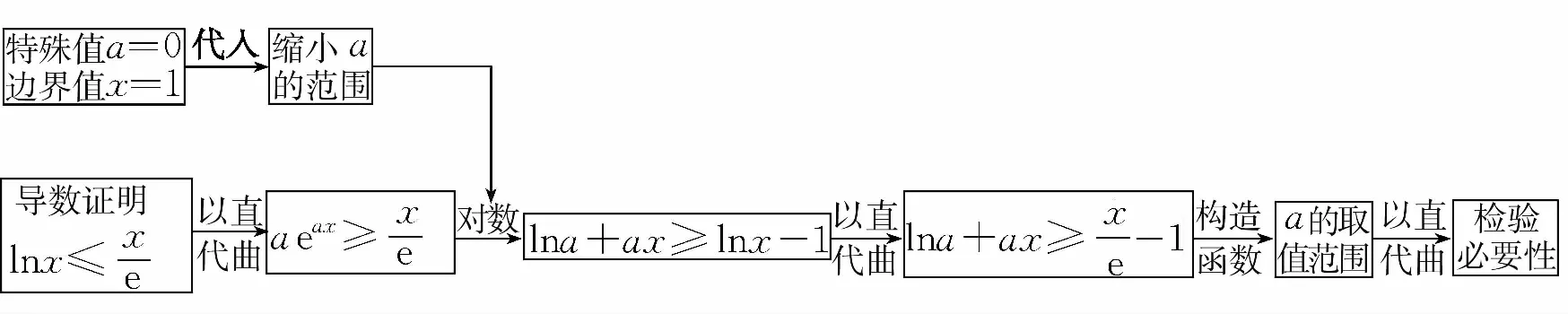
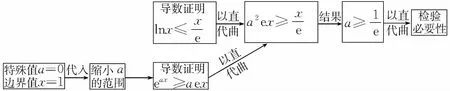
解法二的求解过程分为四个逻辑段.第一个逻辑段:由特殊值缩小a的范围;第二个逻辑段:由相切构造方程组;第三个逻辑段:消元解方程组;第四个逻辑段:由a的几何意义结合临界值得到a的取值范围.其思维导图如下:

心路历程三:解法二的核心是“相切”,由“切”借助导数构造出方程组,难点是解方程组.消元法是解方程组的常用手段,而消元后的方程仍显复杂,再通过取对数、构造新函数解方程.此方法思维量大,运算繁琐,有没有更好的方法呢?
解法二的核心是“相切”,而“切”中的切线是“化曲为直”的一种方法.题目1能用吗?
我们期望找到y=lnx的一条切线y=kx+b,使得lnx≤kx+b,且aeax≥kx+b.这条切线在何方?我们知道y=lnx的切线有无数条,应该选择哪一条?首先否定y=x-1.由图1可以预见,当正数a逐渐变小时,y=aeax逐渐躺平,会有y=aeax的部分图象在直线y=x-1下方.我们期望也找到一条“躺平”的直线,与y=lnx相切.因为y=lnx图象是确定的,所以切线也应该是确定的.
另一方面,aeax≥kx+b两边取自然对数得lna+ax≥ln(kx+b),再次出现ln,这个对数较复杂,我们期望ln(kx+b)经过对数运算后化为“lna+ax(含x的式子)”的形式,这就必然要求y=kx+b中的常数b=0,这样就转化为lnx≤kx,且aeax≥kx,后一个式子取自然对数得lna+ax≥ln(kx)=lnk+lnx,再应用lnx≤kx,得lna+ax≥lnk+kx,所以a≥k.下面就是如何求k.

解法三(以直代曲):仿解法二得a>0.
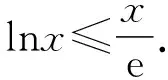

由g′(x)>0得x>e,
由g′(x)<0得1≤x ∴g(x)在[1,e)上单调递减, 在(e,+∞)上单调递增, ∴当x=e时,g(x)取极小值, 也是最小值g(e)=0, 评注:解法三的难点是选择什么样的“直”代“曲lnx”,求解的过程只是展示思维的结果,而看不到是如何想到的. 心路历程四:解法三中“以直代曲”只代换了lnx,能否同时“以直代曲”代换eax? 解法四(两面夹):仿解法二得a>0. 再证eax≥aex,x≥1. 设f(x)=eax-aex,x≥1, 则f′(x)=aeax-ae, ∴eax≥aex,x>0, 心路历程五:解法三“以直代曲”化简条件不等式aeax≥lnx,反复代替,思维逻辑段多,虽然较解法二有了很大改善,但还是不尽如人意.能更简单些吗?命题人想让我们怎么解?再回想分离参数法解决不等式恒成立问题,题目1的难点是如何分离参数.我们能否从结构形式上改造所给不等式,努力让不等式两边的式子“同构”?注意到ax=lneax,因此,在不等式aeax≥lnx的两边同乘x,不等式化为axeax≥xlnx,即eaxlneax≥xlnx,就能达到“同构”的目的,然后就能引入相应的函数,研究函数性质,简化所给不等式,为分离参数做好准备. 解法五(分离参数):在不等式aeax≥lnx的两边同乘x, 得axeax≥xlnx,即eaxlneax≥xlnx, 设函数h(x)=xlnx,x≥1, 则h′(x)=1+lnx>0, ∴h(x)在[1,+∞)上单调递增, 由h(eax)≥h(x)得eax≥x, 两边取自然对数得ax≥lnx, 由H′(x)>0得1≤x 由H′(x)<0得x>e, ∴H(x)在[1,e)上单调递增, 在(e,+∞)上单调递减, 评注:解法五的难点是如何“同构”.同构时要有眼光,同时公式要熟,还要有大胆的尝试精神. 解法五的求解过程分为四个逻辑段.第一个逻辑段:乘x同构不等式;第二个逻辑段:引入函数h(x),利用导数研究函数h(x)的单调性,简化条件不等式;第三逻辑段:取对数,分离参数;第四个逻辑段:引入新函数H(x),利用导数研究函数H(x)的单调性、极值(最值),得到参数a的取值范围.其思维导图如下: 由解法五,我们看到“分离参数法”这一求解不等式恒成立的方法,题目1也是能运用的,只是分离参数不易想到. 心路历程六:解法五告诉我们题目1能用分离参数法求解,那么能用“引入函数,研究函数最值”求解吗?这也是求解恒成立问题常用的通性通法.实际上,也是可行的,只是运算量和思维量较大. 解法六(最值法):仿解法二得a>0. 设P(x)=aeax-lnx(x≥1), 显然P′(x)在[1,+∞)上单调递增, 由P′(x)>0得x>m, 由P′(x)<0得1≤x ∴P(x)在[1,m)上单调递减, 在(m,+∞)上单调递增, ∴P(x)在x=m处取得极小值, 笔者查了网上的解答,也有应用解法六求解的,但其解答过程是将不等式写为方程,其过程是错误的,或者是有待商榷的. 由题目1中的解法二、三、四、六,我们可以看到题目1的自变量x的取值范围可以拓展到x>0,我们得到以下题目2. 【题目2】已知关于x的不等式aeax≥lnx对任意x>0恒成立,则实数a的取值范围是________. 题目2的解答可参见题目1的求解. 笔者思考:题目1为什么要将自变量x的范围缩小到x≥1?是不是也在暗示考生用特殊值法(题目1之解法一)求解?还是为考生挖一个陷阱:代端点值出错?笔者不加妄猜. 将指对互化,可以得到如下题目: 将题目1的解法三中的“直”代换lnx,得到如下题目:

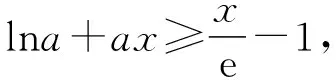
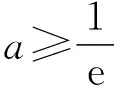

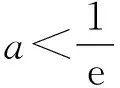
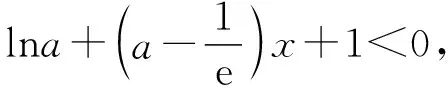
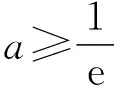
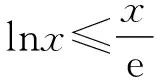
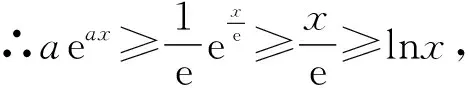
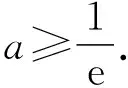

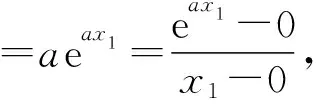
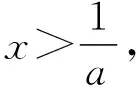
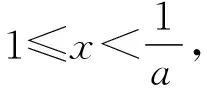
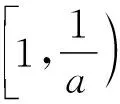
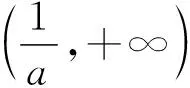
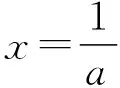
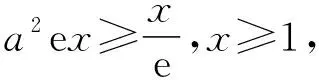
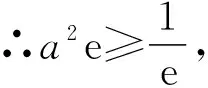
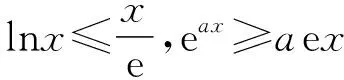
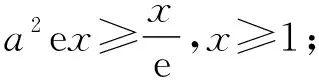
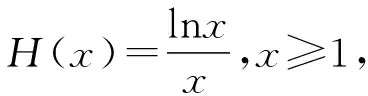



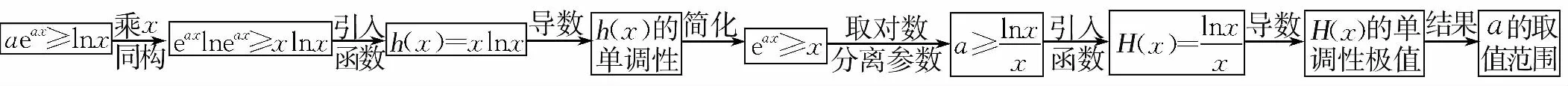

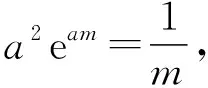
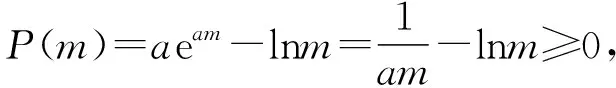

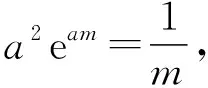
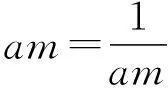
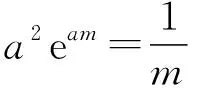

三、拓展