实践性作业:推动学生思维向更深处漫溯
——以“大树身高是多少”为例
江苏省徐州市睢宁县第二中学
孙红梅
《义务教育数学课程标准(2022年版)》指出:动手实践、自主探究、合作交流是学习数学的重要方式.数学学习要实现从书本知识到生活知识的华丽转身,需要在具体的实践当中运用所学的知识,不断地发展数学能力与数学素养.实践性作业就是从学生的“学”开始,抵达数学的“用”,在参与中不断发展操作能力,获得思维的进阶、能力的提升.数学实践性作业既是数学课堂知识的有效强化,也是学生数学生活的充分体验.在实践中,可以不断地发展学生的问题意识,将数学知识与实际生活密切地联系起来,培养学生解决问题的能力.
1 丰富实践猜想,让思维启航
数学伴随着人类生活的始终,是人类思维不断发展、分化的结果,也是人类劳动的重要工具[1].在数学作业设计中,教师要关注数学知识与实际生活的联系.如,近期校园的中心花园新种植了一棵高大的香樟树.这棵郁郁葱葱、茎直挺拔的大树顿时成为了学生关注的焦点.这棵香樟树有多高,也成为了学生关心的问题之一.利用已有的知识进行猜测与验证,是让学生实现数学知识向实际生活转变的内在学习逻辑.
1.1 基于知识的联系性
九年级“锐角三角函数”是初中数学知识的重点,也是难点.在正常的教学活动与作业设计中,教师一般都是直接出示题目,根据已有数据,利用知识原理进行计算,帮助学生巩固知识,使学生具备基本解题能力.从知识的联系出发,将本课的数学方法运用到生活中,基于知识与生活的联系,将这种能力转化为数学实践,不仅能够考查学生对知识的掌握程度,还能够不断指向学生解决问题能力的发展,帮助学生建构起“锐角三角函数”的知识支架.
1.2 基于生活的丰富性
知识来源于生活,服务于生活.在具体的生活实践中,“锐角三角函数”运用范围较广,广泛存在于人们的生产生活中.如,施工队铺设斜坡台阶、船舶离泊应用、车辆测速装置应用等,都需要用到锐角三角函数知识.但这些知识在书本上是“静默”的,需要教师根据知识运用到生活的具体路径,帮助学生实现知识的迁移,让“静默”的知识生动起来,活泼起来,“立”在课堂中央.因此,将一些生活中不能直接测量的数学问题,通过知识的转换,变成可“测量”的问题,既考查了学生解决问题的能力,也丰富了学生学习数学的场景,促进了学生思维的发展.
1.3 基于方法的多元性
解决“大树身高是多少”的方法很多.比如,“测影长法”,即借助同一时间段物体的高度与影长之间的比例关系,通过建立相似三角形,利用“相似比”进行测量;“标杆测量法”,即将“梯形问题”转换为“三角形问题”,采取相似比列方程的方式解决问题;“镜中倒影法”,即根据镜面对称性质,借助三角形相似原理进行对应边的计算,得出结论;还有“直接测量法”等.数学实践活动的作业设计应该是开放的,能够让学生根据学习能力与方法运用选择不同的解决路径.
2 开启实验活动,让思维扬帆
中学阶段学生已经经历了形象思维向抽象思维的过渡,但是对于一些概念性的知识,如果没有经历生活化的建构,就容易处于一种“似懂非懂”的境地.教师搭建实践性作业通道,有助于学生思维活动扬帆远航,让学生在了解知识、运用知识的同时,通过实践性作业深刻感受知识存在的价值与意义,实现知识的有效迁移.
2.1 确立实验目标
在“大树身高是多少”的作业设计时,教师需要从科学的实验方法入手,让学生的思维“活”起来.一是通过具体的操作,利用已有的知识理解测量柱状物体高度的方法,发现其知识依据;二是通过学生的实践参与,不断地发展学生的问题意识,将学生的数学思维从知识向生活过渡;三是借助小组活动,培养学生合作探究的意识.“大树身高是多少”的问题意义不在于具体地了解大树的高度,而是让学生运用数学思维方法,经历“锐角三角函数”知识的建构过程,实现知识的有效迁移,获得能力的有效发展,指向发散性思维的进阶发展与运用.
2.2 进行小组分工
在中学数学实践性作业的实施过程中,教师要关注团队合作的作用.怀特海在《教育的目的》一书中指出:“教育要从个体走向群体,要在集体中发挥大家的智慧,在相互赋能中共同发展.”[2]“大树身高是多少”数学实践作业需要在小组合作学习中完成对“测量”方法的运用.首先,以学习小组为单位,确定测量大树的身高的作业.组长制定本小组测量方案,并组织组员共同研讨,优化方案.其次,准备测量用具.在测量的过程中,测量用具有显性的物质工具,如标杆、卷尺、记录单等;也有隐性的测量用具,如风向、光线、天气等.再次,进行小组成员间的任务分工.有的负责方案设计,有的负责工具准备,有的负责测量结果记录,有的负责表格填写,有的负责数据计算.最后,进行小组总结.根据小组的活动过程,每名小组成员完成一份作业报告.在数学实践性作业的小组分工中,一般是将课堂学习小组分工迁移到实践性作业分工中,这样一方面便于课堂学习有效向课后学习过渡,另一方面也有利于指向小组学习的评价.
2.3 实施操作验证
在具体的操作实验过程中,对于“大树身高是多少”这个问题的探究,学生一般能够运用已有的知识,联系生活经验进行具体的操作探究.主要包括四种方式.
第一种方式(如图1)是将树根与树梢分别确定为A和B,然后将树的投影另一端设置为C,再测量A和C的距离;然后拿一根标杆DE进行投影,测量标杆DE的长度及其影长DC′;最后利用△ABC∽△DEC′,计算得出大树的高度.

图1
这个实践操作活动,有利有弊.优点在于操作简单,易于测量;缺点在于操作实践耗时较长,易受天气的影响.在这个过程当中,教师可以引导学生思考有没有什么方法能够解决测量中遇到的问题.学生进行小组讨论,借助“比”的性质,还可以优化测量方法.
第二种方式中,小组成员也利用了“太阳”,但是巧妙地利用了“同一时间段,物长与影长比值一定”的性质,以小组成员身高为参照物,测出大树身高,如图2.在这个小组活动中,为了更加接近树高的精准数值,小组4名成员先后作为“参照物”上场,测出大树的高度分别为15.7 m,15.9 m,15.5 m和15.6 m,经过计算平均值,得出大树高度为15.7 m.
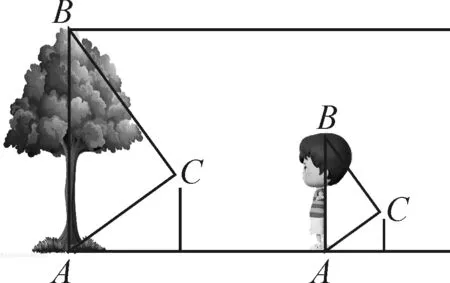
图2
第三种方法则显得“简单粗暴”,小组成员找来了三根竹竿,小组成员将竹竿绑在一起,然后将竹竿在与大树平行位置立起来,通过测量竹竿的长度得出大树的高度.在实践操作中,学生的观察由于受到视线的影响,误差较大.为了解决这一问题,小组成员决定在教学楼五楼的走廊观察,但是距离较远,同样影响了测量的精度.
第四小组则是在地面任意一高度设置高为CD的测角仪,测量得到大树树梢B的仰角为a,而DE等于AC,AC直接通过卷尺测量就可以精准得到具体的数值,如图3.然后通过正切求出BE,进而求出AB.在小组的实际操作中,组员为了能够让数值更为准确,还设置了不同位置的点C,通过几组数据求出平均值,得出大树的高度为15.7 m.

图3
数学实践性作业的本质就是让学生进行自主实践,在具体的实践活动中发现问题,解决问题,验证猜想.在实践过程中,教师也需要进行有效的指导.如,有的小组在测量时,没有“太阳”,怎么办;竹竿长度不够,如何解决;测角仪的使用是否科学;等等.这些都应该纳入实验操作的关键环节予以必要的关注,把实验活动引向成功.让学生不仅知道在操作过程中做了什么,而且要知道为什么做这些,不断培养学生思考、推理、想象能力.
2.4 结论展示交流
当实验操作结束后,进行展示交流可以有效地将活动引向思维的发展.在展示交流中,一是展示优秀的作业报告,作业报告既要记录实验的主要操作过程,也要得出接近大树高度的测量结果;二是教师要从知识的转换与应用角度进行评价,让学生能够在运用知识的过程中总结出不同的方法与规律,指导学生学以致用;三是在小组交流讨论中,不断让学生在借鉴当中完善实践活动,能够在更丰富、更广阔、更多元的思维活动中获得数学能力的发展与进阶,进而提升对当下知识的理解与运用能力.
3 感受活动价值,让思维抵达
实践性作业是以学生为主体、知识为载体,以能力发展为目标的综合性活动.在中学实践性作业设计中,需要从学生数学核心素养的发展出发,通过具体的实践活动,感受活动的价值,使学生的思维抵达具体的实际生活.
3.1 指向数学抽象与逻辑推理
在“大树身高是多少”的数学实践活动中,数学抽象要从数量与数量关系出发,在具体对大树身高知识的研究当中抽象出普遍规律,并且让学生通过具体的数学知识予以呈现.在这样的学习过程中,学生的理性思维得以发展,抽象能力得以培养,问题意识得以强化,有利于学生将具体的数学知识在实际活动中形成知识结构.实践性作业需要学生设计,设计的过程就是逻辑推理的过程[3].设计的活动必须符合测量物体高度的一般方式.在准备测量用具的过程中,也需要学生从探究“大树高度”这一知识的本源出发,发现实验的基本目标,掌握实验的基本形式,推理探究的基本过程,建构准确的实验结论,进行有效的表达与交流.
3.2 指向数学建模与数学运算
数学建模是指在具体求大树高度的过程中,从数学的视角提出大树身高是多少的问题,运用已有的数学思想进行分析,用精准的数学语言进行描述.这个过程就是模型建构的过程.教师还需要从学生的数学经验出发,但又不囿于已有的经验,能够不断地进行创新.实践性作业离不开计算,“大树身高”需要具体的运算,在这一过程中,学生需要准确地掌握相关的运算法则,选择合适的运算方法,求得准确的运算结果,得出真实的实践结论.
3.3 指向直观想象与数据的分析
直观想象主要表现在探究过程中空间想象与感知能力的发展.在解决大树身高是多少的过程中,基本上都需要运用到几何图形.在实践过程中,学生通过具体的图形来进行分析、推理、论证,有助于发现解决问题的辅助手段.最后是数据的分析.学生通过研究能够获得有效的数据,这些数据的作用显然不是仅仅获得大树的身高,还要基于这些数据能够在生活中解决实际的问题.比如,通过不同年份大树身高的变化,分析了解大树的生长情况.在数学实践性活动中,“活动”只是知识的载体,更需要从能力发展与品格提升角度进行综合考虑,指向学生的全面发展.
总之,初中实践性作业需要从学生必备品格与关键能力的发展出发.摒弃传统的作业观,在“双减”背景下,真正指向学生综合能力的发展;设计出更丰富的、更有趣的、更多元的实践性作业,让学生在实践过程中增长知识、发展思维,提升能力.体验完整的数学化生活,既是课程的使然,也是时代的要求.

