巧用“两招”,破解数列不等式问题
2023-03-31 05:48施冰洁
语数外学习·高中版下旬 2023年12期
施冰洁

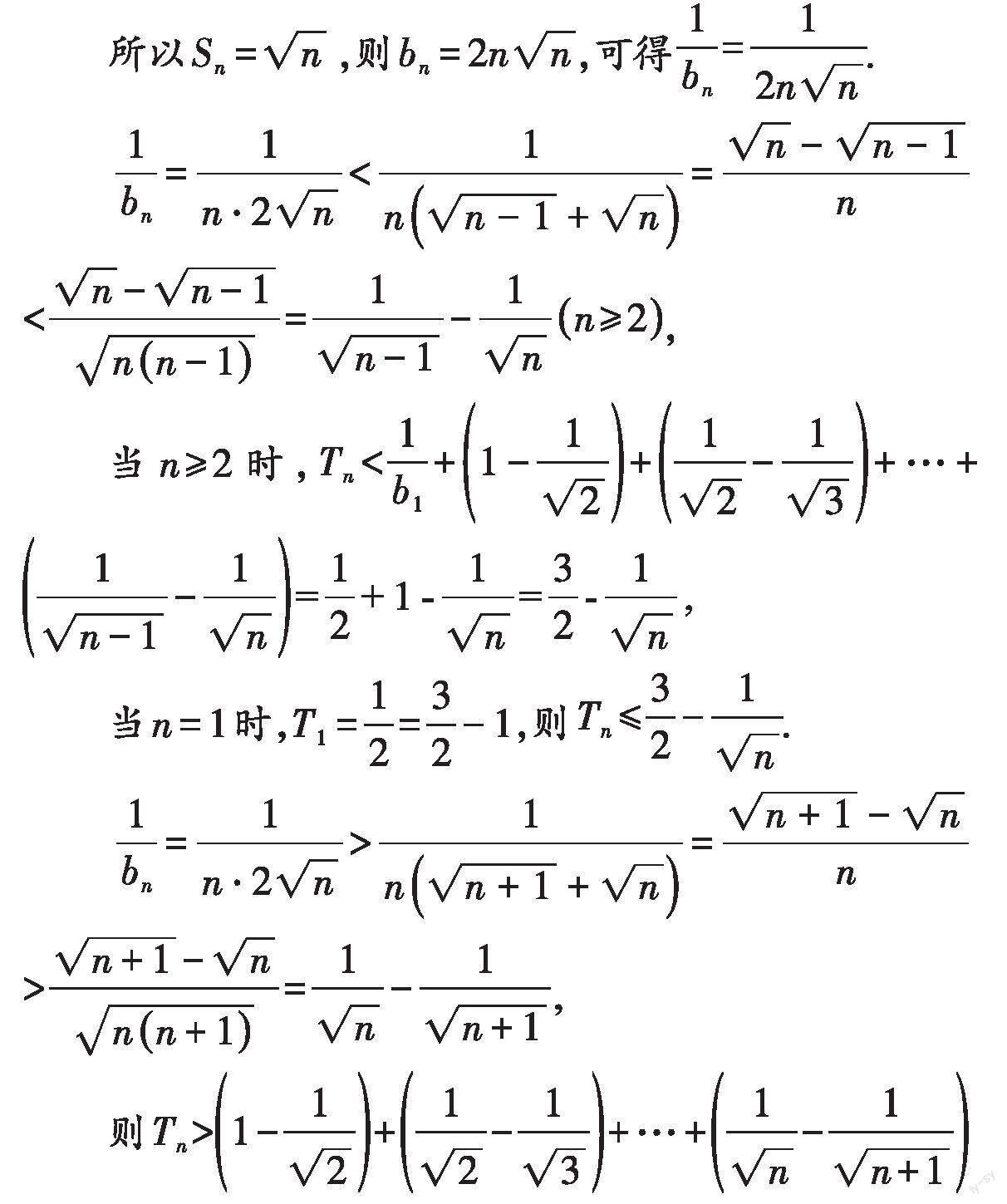

数列不等式问题具有较强的综合性,需综合运用数列、不等式、函数等知识求解.很多同学在解题时不知如何下手.下面结合例题,介绍两个解答数列不等式问题的“妙招”,以供参考.
一、放缩不等式
运用放缩法求解数列不等式问题主要有两种思路,一是将数列的通项公式进行放缩,以将其裂为两项之差,或将其变形为等差、等比数列的通项公式的积与和,再运用裂项相消法、错位相减法、分组求和法等求数列的和;二是先对数列进行求和,然后将所求的和进行放缩,从而证明不等式.
解得[a1=1],即[S1=1],
因为[S2n]为等差数列,所以[S2n=S21+n-1=n],
(1)若[f(x)≤ax+1]在[[1,+∞)]上恒成立,求[a]的取值范围;
二、构造函数
数列是一个特殊的函数,其自变量为正整數.在解答数列不等式问题时,可仔细研究数列各项的变化规律,以判断出数列的单调性,从而根据数列的单调性证明不等式.还可以根据题意构造出合适的函数;然后研究函数的单调性;再利用函数的单调性、最值来证明数列不等式.
虽然数列不等式问题较为复杂,但是我们只要仔细研究数列不等式的结构特征,对其进行合理的变形,研究数列的单调性,灵活运用不等式的性质或重要不等式来对不等式进行合理的放缩,就能顺利证明不等式.
猜你喜欢
新高考·高三数学(2022年3期)2022-04-28
新世纪智能(数学备考)(2021年11期)2021-03-08
河北理科教学研究(2020年3期)2021-01-04
新世纪智能(数学备考)(2020年11期)2021-01-04
中学生数理化(高中版.高二数学)(2020年9期)2020-10-27
中学生数理化(高中版.高二数学)(2020年9期)2020-10-27
河北理科教学研究(2020年2期)2020-09-11
河北理科教学研究(2020年1期)2020-07-24
中学生数理化·高一版(2019年9期)2019-10-12
数学大世界(2017年15期)2017-06-21

