谈谈进行三角恒等变换的技巧

李志辉

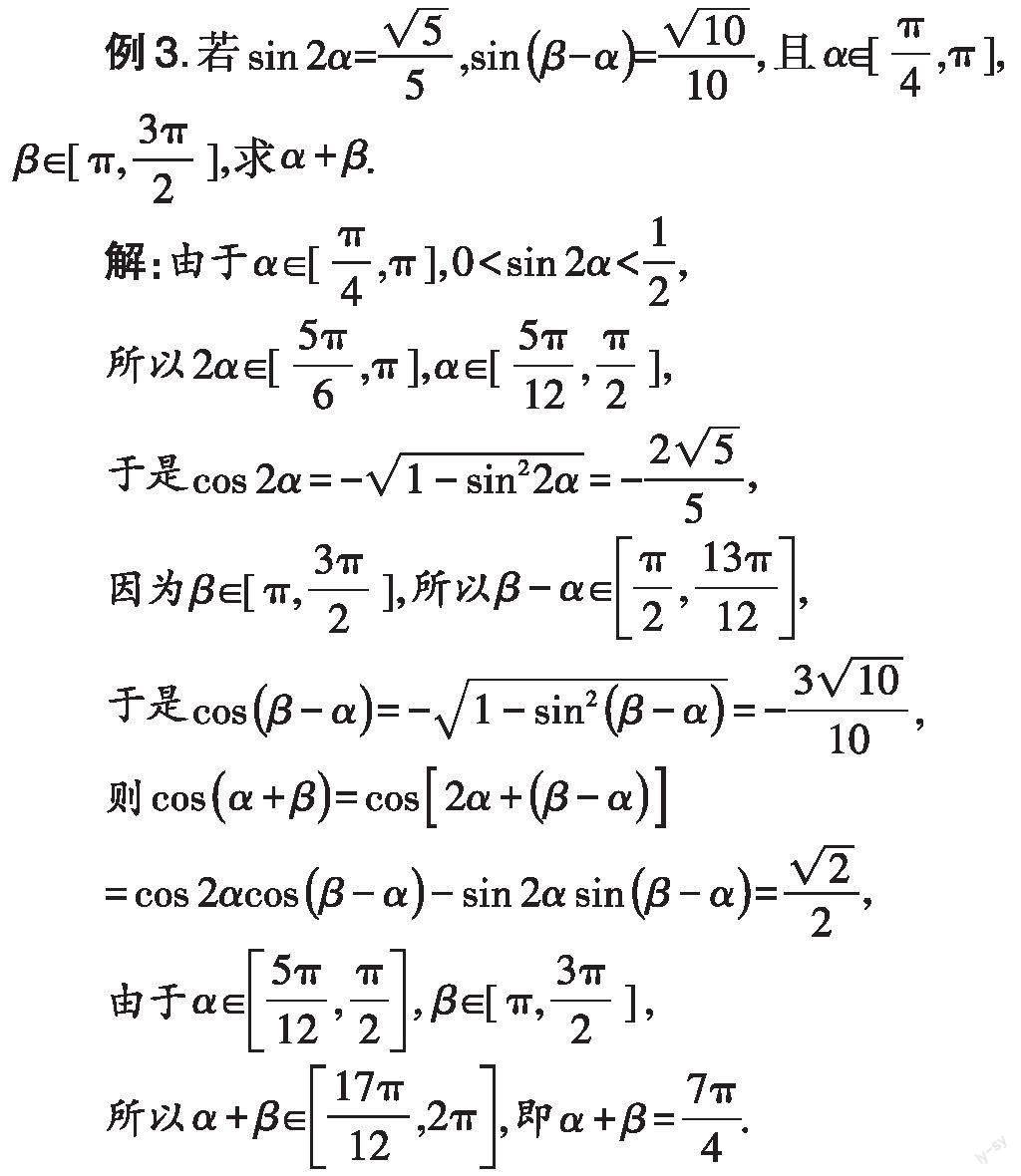
在解答三角函数化简问题、求值问题、证明问题时，经常会用到一些进行三角恒等变换的技巧.熟练掌握一些进行三角恒等变换的技巧，不仅能提高解答三角函数问题的速度，還能发现三角函数公式之间的内在联系，加深对三角函数公式的理解.接下来，通过几个例题，介绍三种进行三角恒等变换的技巧.

一、将异名函数化为同名函数

将异名函数化为同名函数时，往往要先化简所求的式子，将其中的函数名称统一；再将已知关系式中的函数名称与目标式中的函数名称统一.

二、将异次化同次

[=-sin3+cos3+sin3-cos3-1+2cos3=-1].

该函数中含有根式，且含有二次式，需作升幂、降幂处理.于是根据同角的三角函数关系式：[sin2α+cos2α=1]，将函数式中的“1”进行变换，配凑出完全平方式，即可通过开方，将根式化为一次式.再根据降幂公式，将二次式化为一次式，便能将异次化同次.

三、将异角化同角

对于含有多个不同角的三角函数式，通常需通过拆角、补角，将异角化为同角，以减少函数式中角的个数，将函数式化为最简形式.在解题时，要先仔细观察各个角之间的异同；然后进行拆角与补角，如[α=α+β-α]、[2α=α+α]、[2α=α+β+（α-β）]等；再根据两角的和差公式、二倍角公式进行三角恒等变换.

解答本题，要先确定已知角[β-α、2α]与未知角[α+β]之间的关系；然后进行拆角、补角.仔细观察，可发现[α+β=2α+β-α]，利用诱导公式以及两角和的余弦公式，即可求得[α+β]的余弦值.

在进行三角恒等变换的过程中，有时候需同时运用几种技巧，才能使问题获解，同学们需根据已知关系式、目标式的结构特征进行合理的选择.同时还要善于发掘题目中的隐含信息，利用三角函数值确定角的取值范围，以获得正确的答案.