基于协相关性和傅里叶变换-差分吸收光谱法的臭氧浓度在线测量研究

郑海明，姚鹏辉

(1.广东海洋大学 机械与能源工程学院，广东 阳江 529500；2.华北电力大学 能源动力与机械工程学院，河北 保定 071003；3.河北省机电一体化中试基地，河北 石家庄 050000)

1 引 言

天空中浅棕色且带有辛辣刺激气味的气体便是光化学烟雾。其主要成分为臭氧，是由大气中的氮氧化物和挥发性有机物等经光化学反应形成。大气中的氮氧化物和挥发性有机物则主要来源于机动车尾气和化工生产等[1,2]。我国臭氧浓度近年来总体呈缓慢上升态势，臭氧已成为仅次于PM2.5影响空气质量的重要因素。PM2.5与臭氧协同控制已成为我国“十四五”时期环境治理的工作重点，而对臭氧的准确检测则是控制的前提。

臭氧在常温下是1种淡蓝色的气体，它具有特殊臭味，微溶于水，易溶于四氯化碳和碳氟化合物。臭氧是1种强氧化剂，能和许多物质发生氧化反应[3,4]。目前臭氧的监测方法很多，包括碘量法、比色法、化学发光法以及IDS分光光度法等[5,6]，均存在测量不准确、不方便携带且没有相应标气用于实验研究的缺点。

本文搭建了1套在线监测臭氧浓度的臭氧发生装置，并基于协相关性和傅里叶变换-差分吸收光谱法，可对臭氧浓度进行在线监测研究。

2 实验原理

2.1 臭氧发生原理

在臭氧发生器中进行臭氧合成时会发生非常复杂的物理化学反应过程，包括氧原子的形成、臭氧分子的形成与扩散以及臭氧分子的分解等过程。放电时，一定能量的电子使氧分子离解为原子，氧原子再与氧分子碰撞生成臭氧分子，臭氧分子向发生器外扩散时遇到其他的微放电脉冲后引发臭氧分解反应。具体反应为：

(1)

(2)

(3)

(4)

式中M代表反应气体中任何气体分子。

2.2 协相关性和傅里叶变换-差分吸收光谱法

评价变量x和y间线性相关程度的方法之一是通过相关系数ρxy进行描述，其定义为：

(5)

式中：E表示求取均值或数学期望；μx、μy分别为x、y的均值或数学期望；σx、σy分别为x、y的标准差；|ρxy|的大小表明x、y的相关程度。

差分吸收光谱技术以Lambert-Beer定律为基础，吸收截面是分子本身特有的描述气体吸收光强度的量。为了确定这个量，须采用实验的方法进行测量，即在某个温度及压强下，测量1束光通过长度为L且充满一定浓度的待测气体吸收池前、后的吸收光谱[7～9]，再根据以下公式便可得到吸收截面：

(6)

式中N(p,T)代表气体的分子密度，其定义为：

(7)

通过分析不同气体分子吸收光谱的快变部分来得到各组分气体浓度[10]，可由(8)式决定：

(8)

傅里叶变换(Fourier transformation)的核心思想是把信号从时域转化到频域从而体现其频率特征的过程[11，12]。其变换公式为：

(9)

傅里叶变换法就是对式(9)两边进行数值滤波，然后进行傅里叶变换，最后求得浓度的1种方法[13,14]。浓度C计算公式为：

C=RA′(λ)/[Rσ′(λ)×L]

(10)

3 实验装置

3.1 臭氧标气发生装置

为了能够方便准确地研究臭氧相应性质和浓度反演，使用德国SICK公司S710分析仪监测氧气浓度，根据式(1)～式(4)间接推导出臭氧浓度。所创建的臭氧发生装置结构如图1所示。

图1 臭氧标气发生装置Fig.1 Ozone gas generator1—变压器； 2—进气管； 3—出气管； 4—风扇；5—臭氧发生管； 6—流量计； 7—流量调控阀；8—氧气源；9—氮气源；10—箱体；11—出气口

臭氧发生装置包括配气装置和臭氧发生器，其中臭氧发生器有2组，并联在电路中。对2个并联的臭氧发生器分别进行开闭时，产生的臭氧浓度会瞬间发生变化，用于对臭氧发生的浓度进行快速调节。在氧气源与氮气源顶部设置流量调控阀，用于控制气体流量，可对臭氧发生的浓度进行缓慢调节。检测系统用于监测臭氧发生前、后氧气的含量进而可推导出臭氧的浓度。

3.2 光谱分析实验装置

为了研究差分吸收光谱-傅里叶变换原理在线监测臭氧浓度的准确性，排除在特定吸收波段320～350 nm的其它因素干扰，搭建了如图2的实验平台。实验中氙灯发出紫外光经透镜准直，进入样品池，被测量区另一端的透镜汇聚后由单色仪接收信号，单色仪信号则由计算机进行分析处理。样品池长度150 mm、外径40 mm、内径25 mm，材料为聚四氟乙烯，两侧装有透紫外至可见光的石英玻璃窗，另有接口与臭氧标气发生装置相连。

图2 光谱分析实验装置Fig.2 Spectrum experiment device

4 实验结果与分析

4.1 臭氧标气产生

由于现有气体配置厂家并没有臭氧标气的配备和储存，只能对其进行即产即测的研究形式。实验中氧气流量设为10 sccm(standard cubic centimeter per minute,每分钟标准毫升)，氮气流量分别为500、700、1 000、1 200、1 400、1 600、1 800和2 000 sccm，共得到16组数据，如表1所示。

根据式(1)～式(4)，选取氮气流量1 000～2 000 sccm时的数据计算臭氧转化，得到图3。

由图3可以看出，臭氧的浓度具有很好的线性变化，并且精度小于0.1 ×10-6。继续进行下一步实验，即在臭氧特征吸收波段320～350 nm做差分吸收光谱-傅里叶变换分析。

4.2 臭氧吸收光谱的线性相关分析

实验时在流动状态下进行实验数据的采集，采集器的参数如波段和步长的不同，采集时间也不相同。尤其对宽带吸收的气体来说很难把握所采集数据的稳定性，此外还包括光源的不稳定和大气中各种散射如米散射、瑞利散射等的干扰，使得背景谱和吸收谱的选取很难抉择。实验选取了不同波段不同步长下多组实验数据进行分析。对波段200～300 nm(步长1 nm)，215～300 nm(步长0.1 nm)，250～260 nm(步长0.01 nm)以及波段320～350 nm(步长0.1 nm,2次)，各进行了10次重复采集。

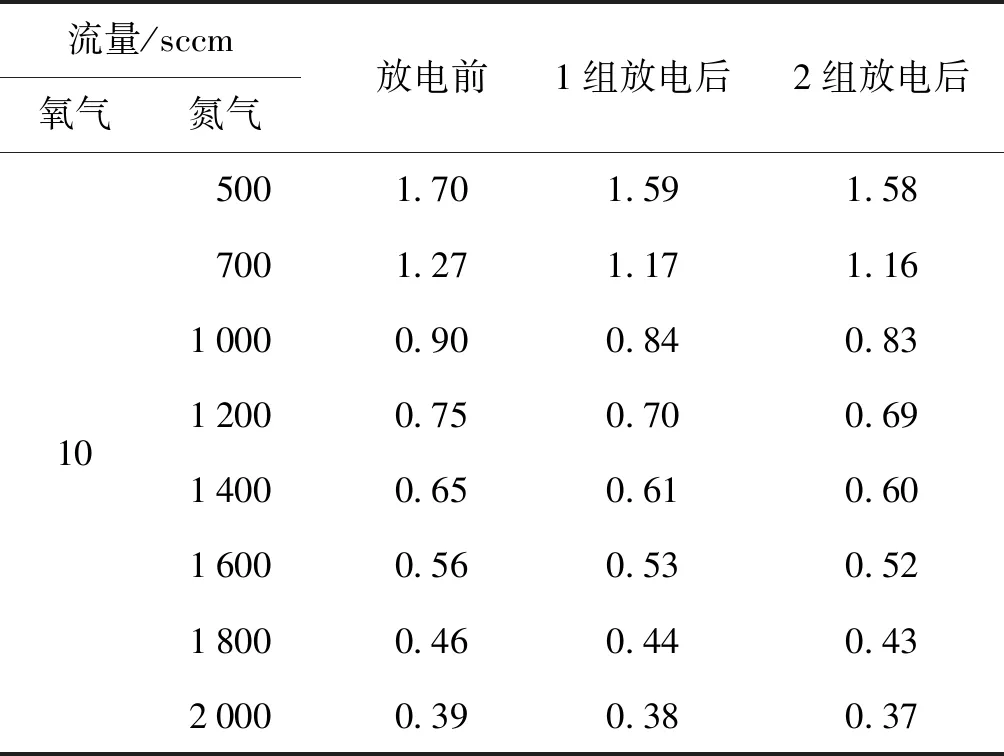
表1 臭氧发生装置氧气含量数据Tab.1 Ozone generator data record (%)

图3 臭氧浓度变化曲线Fig.3 The curves of ozone concentration

实验中每组数据都不相同，其中有变动较大的1组或多组数据，但其总体走势基本一致。造成这种现象的原因可能有：1) 光源的不稳定。尽管实验时使用了稳压电源，但无法排除微小的波动；2) 气流的不稳定。实验时采用数字式流量计，尽量减小其影响；3) 各种散射的存在，无法硬性改善。这样就很难选出臭氧浓度反演的最佳数据，因此进一步采用协相关性的处理办法对采集到的数据进行处理分析，以确定哪组数据最适合浓度反演。在每次实验得到的10组数据中进行两两相关性分析，并将10组相关系数求和。

实验结果如图4，相关组为基础相关组(例如横坐标为1，代表第1组与其他9组分别进行相关分析)。

图4 相关组与其他组相关系数求和柱方图1Fig.4 Column chart 1 of the sum of correlation coefficients between related groups and other groups

图5 相关组与其他组相关系数求和柱方图2Fig.5 Column chart 2 of the sum of correlation coefficients between related groups and other groups

显然，只有相关性较大或数组之间重复性较高时，其和较大(约等于10)。通过两两相关的计算以及相关系数的求和比较，可以看出第2组数据与其它9组实验数据的协相关系数之和很接近10，且系数之和最大，为最优组，因此选取该组数据进行后续计算。此次实验完成最优组选取后，其它实验是否也是如此，需要进一步验证。如图5(柱方图2)所示波段215～300 nm、步长0.1 nm实验数据处理结果。通过比较，可以看出第9组数据与其他9组实验数据的协相关系数之和最大，因此选取该组数据进行计算。另外，图5每一组相关系数求和较图4中数据更接近于10，说明图5的实验状况要优于图4的实验状况，更有利于气体浓度的反演，而实际情况下只需尽量保持工况稳定即可。

随后对其它几次实验做同样的处理，并找出最优组和最劣组。由表2可得，每次实验的最优组为随机分布，但总的来说出现在后几组的机率较大，说明平时进行多次实验后选择1组实验数据进行臭氧浓度的反演是有效的，但不一定都出现在后面几组，结果往往具有偶然性，这也是造成臭氧浓度反演不稳定的原因之一。

表2 不同实验数据处理结果Tab.2 Different experimental data processing results

为使计算结果更准确，进行协相关性处理是最直接有效的。根据Hitran数据库查得常温下臭氧吸收截面后，将其5个峰值点与图5中最优组和最劣组臭氧吸收截面的计算结果进行比较，如表3所示。

由表3数据可以看出，计算误差均小于10%，在标准允许误差范围内，说明实验系统的可行性和计算的准确性。另外通过最优组和最劣组的比较可以看出，虽然257.2 nm处的最劣组优于最优组，但总体来说对多组数据进行协相关性分析有利于计算准确性的提升，即证明在进行数据的计算时经协相关性分析可优化臭氧浓度的反演过程。

4.3 臭氧光谱的差分吸收光谱-傅里叶变换研究

根据差分吸收光谱原理，可在320～350 nm特征吸收波段排除臭氧以外其它组分的干扰，也可减小由于光源发光的不稳定，以及在大气中一般存在的各种散射如米散射、瑞利散射等的影响。随后运用傅里叶变换和逆傅里叶变换解决噪声干扰问题，对处理后的信号再次进行傅里叶变换并建立最大幅值与标气浓度之间的相应曲线方程，这样就能够快速、准确的计算出臭氧浓度。如图6，为臭氧吸收截面与差分吸收截面曲线。可以看出臭氧在320～350 nm波段的吸收很微弱，直接反演臭氧浓度有一定的难度，这也是为何要进行2次傅里叶变换并去除噪声信号的原因，同样对于吸收微弱的波段去除噪声的干扰是很有必要的。

选取图6中差分吸收截面最高吸收峰，发现各峰之间的间隔约为2 nm，拟定300 nm为1个吸收周期进行傅里叶变换和逆傅里叶变换。如图7为原始信号与处理后信号对比。噪声信号是随机的，不重合部分表示噪声干扰较大。

表3 不同吸收截面数据对比Tab.3 Comparison of different absorption cross section data 10-17 cm2

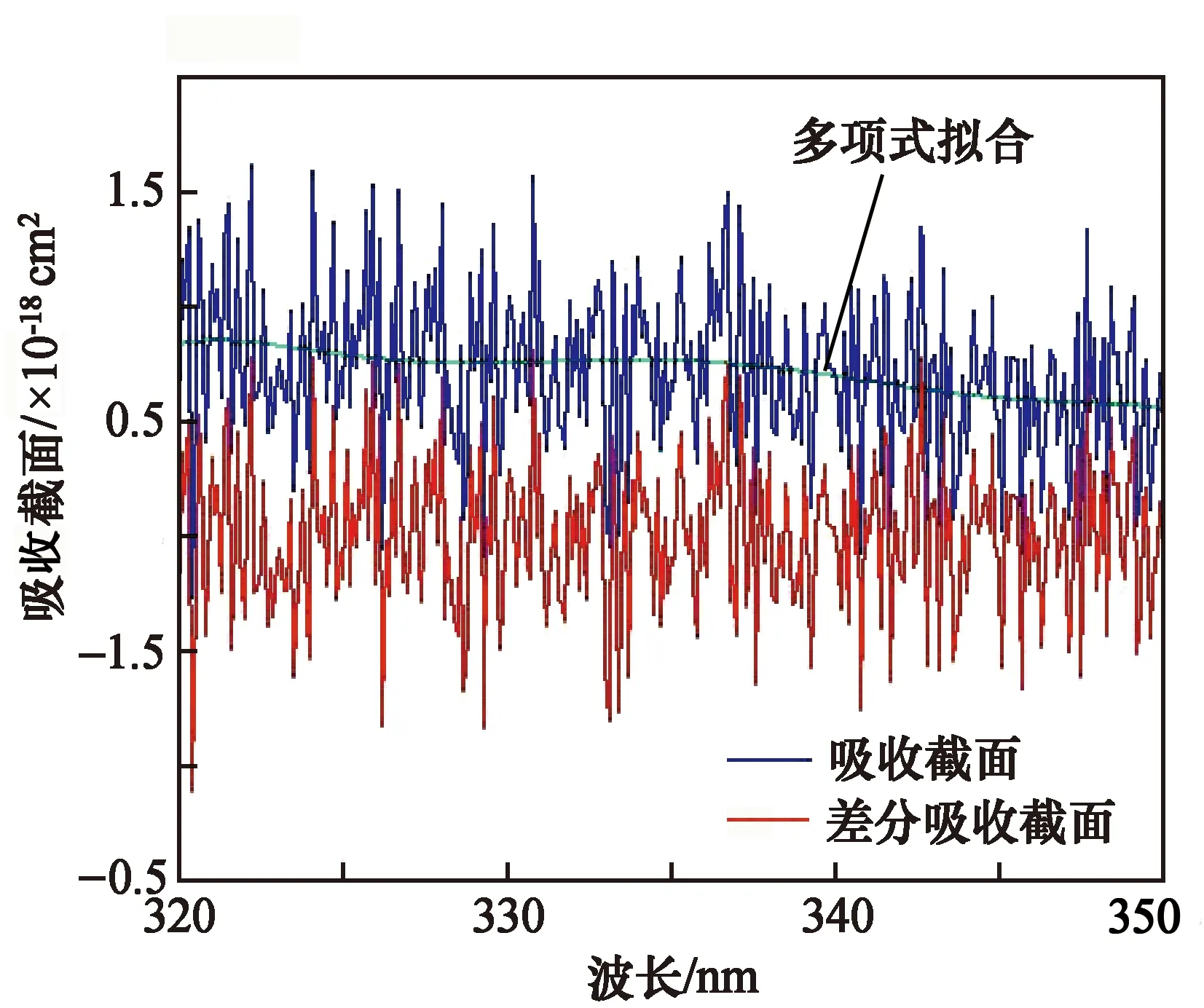
图6 臭氧吸收截面与差分吸收截面曲线Fig.6 Ozone absorption cross section and differential absorption cross section curve

图7 信号处理对比曲线Fig.7 Contrast of signal processing curves

将处理后的信号再次进行傅里叶变换计算，拾取其中最大值，建立了如表4所示的变换幅值最大值与臭氧浓度的对应关系(前2列)。

对表4中的前2列数据分别进行一次和二次拟合，得到拟合曲线分别为：y=105.2x-8 610(相关系数R2=0.992 7)和y=-4.003x2+775.9x-3.67×104(相关系数R2=0.993 6)，其中x代表傅里叶变换最大幅值，y代表臭氧浓度。选取相关系数R2=0.993 6的曲线作为臭氧浓度反演方程，其反演结果见表4的后2列，反演误差小于6%。

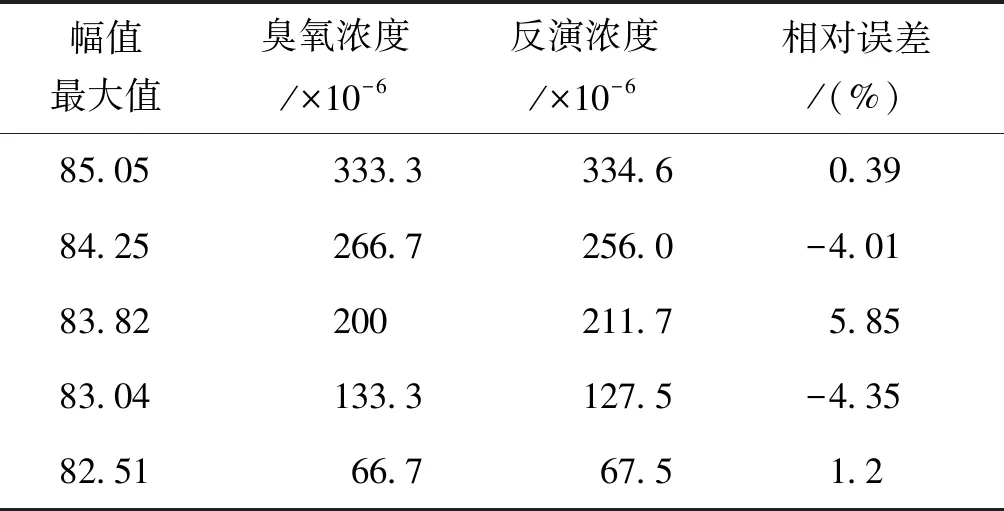
表4 变换幅值与臭氧浓度对应关系Tab.4 Corresponding relationship between transformation amplitude and ozone concentration

5 结 论

创建了一套能够用于实验室在线监测臭氧浓度的发生系统，然后应用协相关性对实验测得的多组背景谱和吸收谱进行分析，得到最优背景谱和吸收谱，优化了臭氧吸收截面和浓度的反演。最后采用差分吸收光谱和傅里叶变换法成功建立了臭氧浓度反演方程。

尽管优化了臭氧吸收截面的反演过程并成功建立了臭氧浓度反演方程，但在优化处理过程中需要采集多组数据，耗时较长；在噪声信号的处理问题上仍然有误差并且频率的选取有一定的偶然性。