铯喷泉钟C场的测量与计算

刘洪康，刘 昆，韩 蕾，房 芳，陈伟亮，郑发松，戴少阳，左娅妮，李天初,

(1.北京理工大学光电学院，北京 100081； 2.中国计量科学研究院，北京 100029)

1 引 言

SI单位“秒”，作为国际单位制的基本单位中最早量子化的单位之一，测量准确度在7个基本单位中最高。铯喷泉钟作为复现秒定义的基准装置[1～3]，不确定度达到10-16量级[4，19]。

铯喷泉钟采用激光冷却技术[5]将铯原子冷却到μK量级[6]，并利用原子上抛下落过程中两次与微波相互作用，实现Ramsey跃迁[7]。为保证原子在与微波相互作用和自由飞行时不受外部磁场影响，需要设计性能良好的磁屏蔽系统，使磁屏蔽内部磁场降到nT量级。同时在磁屏蔽内部需要建立一个弱磁场，以便在微波与原子相互作用时为原子提供一个量子轴方向，即C场[8]。C场的磁感应强度小且均匀，可以使处于简并状态的原子基态能级发生塞曼分裂[9]。为了使C场尽可能均匀，要把通电螺线管组成的C场组件放置在屏蔽效果良好的多层磁屏蔽的中心，而且在C场线圈上下两端增加电流可调的补偿线圈。本次实验中为NIM6铯喷泉钟[10]的喷泉钟磁屏蔽做了新的设计[11]，磁屏蔽系数达到104量级。

C场分布是确定二阶塞曼效应引入不确定度的关键，二阶塞曼频移是喷泉钟评定中最大的频移项[12]，所以C场分布的测量和计算方法十分重要。在不破坏铯喷泉钟物理真空系统前提下，C场的测量只能使用间接测量方法，常用的有两种，喷泉管顶端低频天线法[13]和微波激励法[14]。其中微波激励法就是改变向上向下光的失谐频率，将原子上抛到不同高度，利用磁敏跃迁|F=3，mF=1〉至|F=4，mF=1〉的频移计算磁感应强度。此处得到的磁感应强度是原子飞行路径上经时间加权后的平均磁感应强度。

为了获得C场不同高度的磁感应强度分布，需要对时间加权的平均磁感应强度进行去加权计算。本文针对去加权计算引入了两种计算方法，先用仿真数据对两种去加权计算方法进行了理论验证，最后利用微波激励法和两种去时间加权方法对铯喷泉钟C场的不同高度的磁感应强度进行了测量和计算。

2 测量原理

C场在各个高度的磁感应强度的微波激励测量方法就是改变向上向下光的失谐频率，将原子上抛到不同的高度获得不同上抛高度磁敏跃迁的Ramsey条纹，并确定Ramsey条纹的中心峰的跃迁频率。铯原子超精细能级|F=3，mF=m〉与|F=4，mF=m〉之间有7个σ跃迁(m=-3,-2,-1,0,1,2,3)，根据Breit-Rabi公式[15]，跃迁频率为：

(1)

式中：νhfs=9 192 631 770 Hz，为铯原子基态无干扰跃迁频率；x是Ramsey场无量纲参量，与磁场磁感应强度B成正比：

(2)

νz=ν1-νhfs+ο(B2)

(3)

式(3)中的磁场应为冷原子飞行路径上经时间加权的平均值。

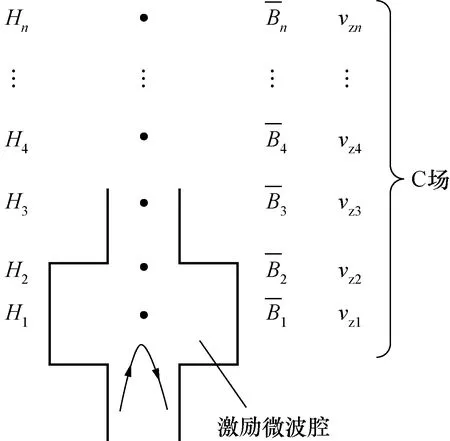
图1 C场不同高度的磁感应强度测量方法示意图Fig.1 Schematic diagram of the measurement method of magnetic induction intensity at different heights of C field

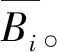
3 去时间加权计算方法

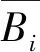
3.1 一级近似计算方法

随飞行时间的平均磁场满足：

(4)

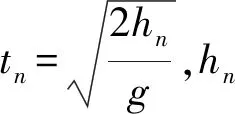
n=1,2,3，…

(5)

式中：Δtn,k为原子上抛到高度hn过程中，所经过第k个C场点Bk的作用时间，记为：

(6)

边界条件为：h0=0。转换为矩阵形式为：

(7)

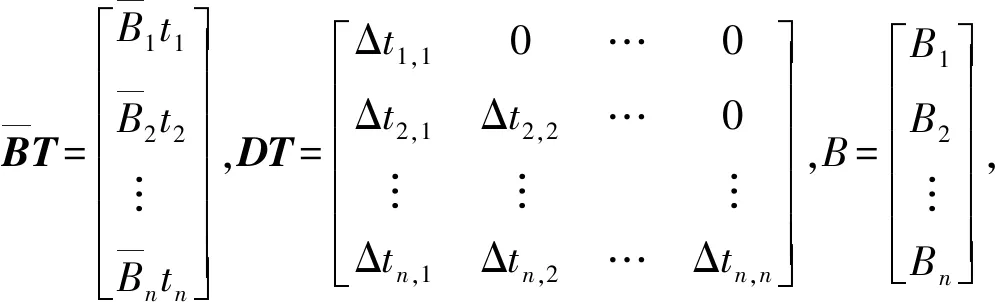
(8)

3.2 二级近似计算方法

第一种方法包含大量如式(6)对上抛时间的计算，相对繁琐。当上抛高度间隔一致时，进一步简化，可以省略掉上抛时间的计算，直接构建出转化矩阵。因为此方法使用了两次近似，所以称此方法为二级近似方法。

具体来说，原子上抛到高度hn(n=1,2,3,…)时，测量得到的平均磁场转化为高度积分：

(9)

时间t与高度x的关系可由自由落体公式推出：

(10)

对式(10)求导得：

(11)

然后代入到式(9)得：

(12)

再将式(12)离散展开为：

(13)

初始值设为：h0=0。当相邻两上抛高度的差即Δh恒定时，hn=n×Δh，代入到式(13)中可得：

(14)

此时，高度信息也抵消掉，随时间的平均磁场值直接跟上抛测量次数n相关，式(14)中定义：

(15)

fn,k为离散化系数，由于离散化前式(12)中的系数满足：

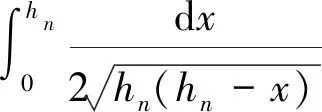
=1

(16)

而离散化处理时，离散化系数的和不等于1，需要将fn,1,fn,2,…,fn,n归一化处理，转化为Fn,1,Fn,2,…,Fn,n，即：

(17)

可得到矩阵表达式：

(18)

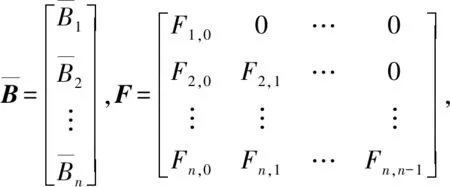
(19)

3.3 两种计算方法的理论验证

一级近似方法在式(5)处离散化时进行了一次近似，而二级近似方法在式(13)处离散化和式(17)处归一化处理时进行了两次近似，从近似程度上来讲，一级近似方法比二级近似方法更加准确。

但从计算强度上来说，一级近似方法构建的矩阵DT较为复杂，使得程序的编写更加繁琐。而二级近似方法在满足每次测量增量相同的条件下，便可忽略上抛高度及上抛时间等参量的计算，构建矩阵F可以直接使用自然数构建，因此程序更加简洁，通用性更好。

考虑C场随高度变化周期性波动的情形，以偏置120 nT，幅值0.5 nT的sin函数来仿真磁场随高度变化的波动，其周期代表波动频率。周期越小，波动越剧烈；周期越大，波动越平缓。仿真图形如图2所示。

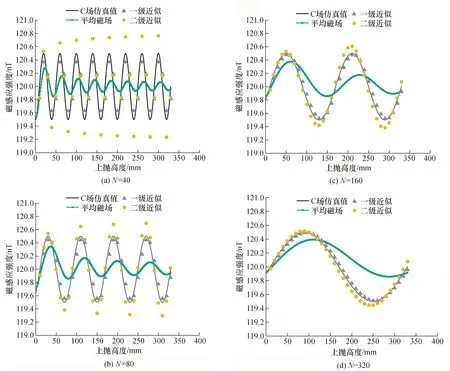
图2 仿真不同波动周期的磁场验证两种去时间加权算法的有效性Fig.2 Simulation of magnetic fields with different fluctuation periods verifies the effectiveness of the two de-time weighting algorithms

图2中，仿真了4种不同的波动周期，分别为N=40,80,160,320，C场不同高度磁感应强度仿真值如图2(a)、图2(b)、图2(c)、图2(d)中细线所示，高度以激励微波腔中心为原点。利用式(14)可以计算得到经时间加权的平均磁感应强度值，如图2中粗线所示。设置上抛高度的间隔为10 mm，通过两种算法计算得到C场推算值，一级近似方法和二级近似方法分别如图2中三角形散点和圆形散点所示。

由图2中结果可以看出，磁场波动越剧烈，两种算法的差异就越大，N=40时两组推测值相差最大，最大值为0.40 nT；波动越平缓，差异越小，N=320时两组推测值差异最小，最大值为0.12 nT。因此，在C场波动比较平缓的情况下，两种方法所得推测值差异并不大。波动程度相同的情况下，尤其是在N=40的极值点附近，二级近似算法所得推测值比一级近似算法波动更剧烈，且一级近似算法所得结果更接近于真实值。

4 实验测量与数据处理

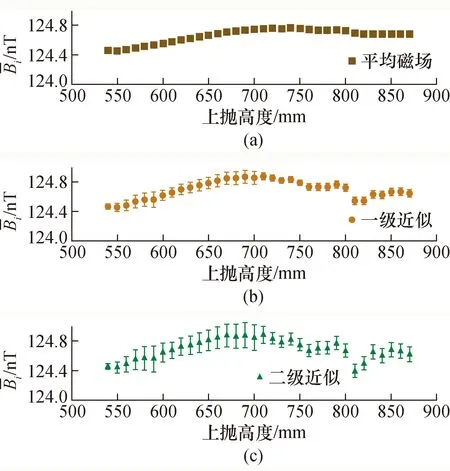
图3 不同方法获得的磁感应强度Fig.3 Magnetic field strength obtained by different methods

通过对两种去时间加权算法编写程序，分别得到式(8)、式(19)中的DT矩阵和F矩阵，其值为：

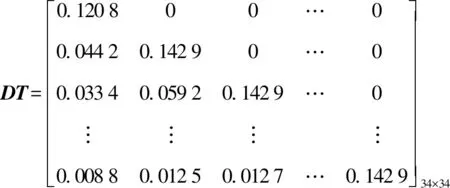
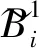
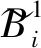
图4比较了两种算法的相对差值，从图3和图4的结果来看，两种算法计算存在一定差别，特别是在极值点附近，二级近似算法计算结果波动更大一些，而且标准不确定度也大一些。两种方法所得结果的相对差值最大为0.11%，实验结果与理论计算一致。这主要由近似程度不同造成。

根据式(1)和式(2)，可以得到铯原子喷泉钟二阶塞曼频移计算公式为：

(20)

式中：〈B2〉为原子干涉期间感受到的磁感应强度平方的时间加权平均值。

根据式(20)和蒙特卡洛方法计算出两种算法下的磁感应强度分布的估计值，可以得到两种算法下二阶塞曼频移的差值为3.7×10-18，远小于铯原子喷泉钟的10-16量级的不确定度，因此两种算法均可在喷泉钟实验中使用。

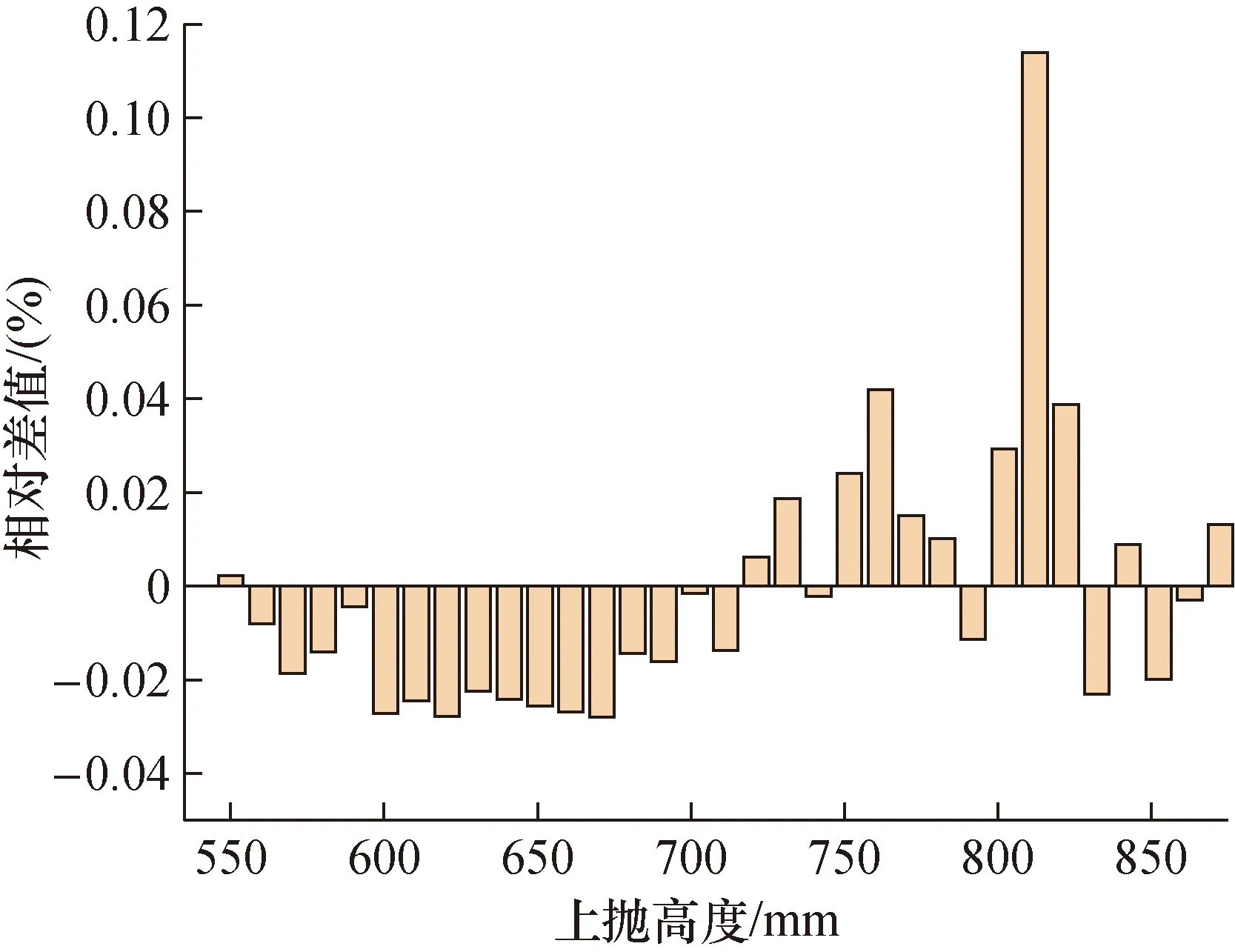
图4 两种方法所得结果的相对差值Fig.4 The relative difference between the results of two methods

5 结 论

微波激励法测量铯喷泉钟实验中C场的磁感应强度得到的是经时间加权的磁感应强度的平均值。本文针对去时间加权，在不同近似程度上引入了两种计算方法，并在理论上对两种算法进行了仿真验证。最后，使用微波激励法测量了NIM6铯喷泉钟的C场分布，对经时间加权的磁感应强度平均值进行了不确定度评定。利用蒙特卡洛方法计算了两种去时间加权算法下的C场的估计值及其不确定度。结果表明，两种算法得到的结果相差不大，两种算法均可在喷泉钟实验中应用。