音速喷嘴一元流动模型详解及其激波计算

沈昱明, 田 童

(上海理工大学,上海 200093)

1 引 言

文丘里音速喷嘴(以下简称喷嘴,或CFVN),作为传递基准或工作基准,常用于对气体流量计的标定或计量、校准。音速喷嘴的临界背压比,或最大允许下游压力一般通过实验方法确定[1]。文献[2]讨论了最大背压比(maximum back pressure ratio,MBPR)与喷嘴的几何尺寸、雷诺数和气体参数的影响,并用A14喷嘴进行了实验；文献[3]使用CFD数值模拟讨论了音速喷嘴下游管路对临界背压比和流出系数的影响,发现在喷嘴的扩散段出现激波现象；文献[4]采用实验方法研究了提高临界背压比的方法；文献[5]从一元等熵流动理论出发,证明了音速喷嘴的临界流流量公式,但其证明过程存在瑕疵；文献[6]对一种二维长方形喷管进行了实验研究,以确定喷管扩散段中产生的激波参数。

本文从一元等熵流动理论出发,从数学上推导了:当喷嘴达到临界背压比时,喷嘴喉部(最小截面处)的流速为当地音速,质量流量达到最大值。推导过程弥补了文献[5]的瑕疵。详细阐述了临界压比、临界背压比,以及出口压力和背压的关系,并给出了相应的一元等熵流动理论计算模型。详细推导了实际条件下音速喷嘴的质量流量公式。本文还从气体动力学基本方程出发,讨论了喷嘴扩散段产生激波的机理,并作了详细计算,包括激波产生的位置、激波前、后的马赫数和压力;采用数值模拟方法和文献[6]提供的实验数据,对计算结果进行了验证。从计算和实验结果知,在较大背压比范围内,音速喷嘴扩散段将产生激波,并伴随产生压力波动。当喷嘴工作在设计条件时,喷嘴内部不产生激波,这时音速喷嘴达到稳定的工作状态。

2 音速喷嘴的一元等熵流动模型

2.1 临界流证明

当背压足够小时,通过喷嘴的质量流量达到最大值;喷嘴喉部达到临界流速,即音速。文献[5]的证明流量公式仅在喷嘴喉部,失去了一般意义。

设气体为完全气体,或称为理想气体,则理想气体在喷嘴中作一元等熵定常流动时,经过喷嘴的质量流量qm和喷嘴任意截面上的流速c分别为:

(1)

(2)

(3)

式(3)说明:当达到临界压比γ*时,式(1)取得最大值,p*为临界压力。

将式(3)代入式(2),得到临界流速为:

(4)

2.2 一元等熵流动方程

无论是否达到临界流,对于理想气体一元等熵定常流动而言有式(5)所示关系(产生激波除外)。

(5)

式中:ρ为喷嘴任意截面上的气体密度;T为气体绝对温度;R为气体常数。未知量为p、ρ、c、T,因此式(5)所示方程组封闭。

产生激波后,熵增加,滞止压力减小,但总能量保持不变。激波后的滞止压力p0d与激波前喷嘴上游滞止压力p0u(即p0)的关系在第5.2节讨论。激波前后的滞止温度不变,即T0=T0d。激波后仍满足等熵流动,故将p0d、T0d、ρ0d代入(5)式,即可计算激波后的流动参数。

3 实际条件下的质量流量公式

3.1 ISO 9300中流量公式

ISO 9300标准中,理想气体和实际条件(real conditions)下气体的最大质量流量分别为[1]:

(6)

(7)

3.2 公式推导

根据连续性方程,流过喷嘴的质量流量为:

qm=Aρc

(8)

考虑实际条件,通过引入压缩性系数Z对完全气体状态方程进行修正[1,7]:

p=ZρRT

(9)

将式(9)代入式(8),得到:

假设喉部达到音速,即Mant=1。引入Cd’(考虑粘性等非理想气体因素影响)和C*(考虑实际气体种类的影响,取代C*i),得到实际条件下气体的最大质量流量为:

(10)

4 临界压比与背压比

4.1 定义

ISO 9300的2.48和2.49条分别定义了临界压比和背压比(back-pressure ratio,BPR)。其中,临界压比γ*是指当经过喷嘴的气体质量流量达到最大值时,喷嘴喉部静压力与喷嘴滞止压力之比[1],由式(3)计算得到。对于空气等双原子气体,γ*=0.528 3。背压比是指喷嘴出口静压力与喷嘴上游滞止压力之比[1]:

(11)

式中:pe为喷嘴出口断面上的气体压力;Mae为出口断面上的马赫数。

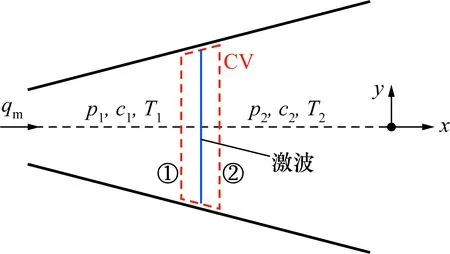
当喷嘴出口气流达到超音速时,称为设计条件[8～12]。当背压比高于设计条件时,pe=pb;而当背压比低于设计条件时,pb

4.2 最大背压比

第2节已证明,当喷嘴刚好达到临界条件时,喷嘴喉部达到音速,流过喷嘴的气体质量流量达到最大值,此时的背压比即称为最大背压比(maximum back pressure ratio,MBPR)[2];ISO 9300则称为最大允许下游压力(maximum permissible downstream pressure)[1],其含义与MBPR是一致的。而文献[4]则称其为临界背压比(critical back pressure ratio,CBPR)。无论是MBPR还是CBPR,均是指喷嘴背压与喷嘴上游滞止压力之比;临界背压比≠临界压比,不能使用式(3)计算。由于临界背压比容易与临界压比相混淆,故本文采用MBPR的表述。

ISO 9300给出了最大允许下游压力MBPR的计算公式(Re>2×105)为[1]:

(12)

当喷嘴喉部达到音速时,出口界面上的马赫数Ma2仅与喷嘴面积比有关,由式(13)计算。

(13)

图1 文丘里音速喷嘴的RmbpFig.1 MBPR for CFVN

5 激波产生机理与计算

5.1 空气动力学工作机理

为了便于验证,本文采用文献[2]中A14喷嘴进行讨论。喷嘴的结构参数为[2]:喉部直径d=0.8 mm,扩散段长度l=8.4d,扩散段半角θ=2.5°。

图2 文丘里喷嘴的压力、马赫数曲线Fig.2 Pressure and Mach number curve for CFVN

当背压比进一步降低,直至在喉部刚好产生临界流,如图2中③所示。这时,pe=pb,扩散段仍全部为亚音速。

继续降低背压,如图2(a)中④、⑤所示,这时仍然满足pe=pb。但是,这种情况下,在喷嘴的扩散段中的某处产生激波。这时,连接喉部的扩散段一部分为超音速,一部分为亚音速;压力出现间断性[8～10]的突变而迅速上升,这种现象称为流体过渡膨胀[10]。之后,流动仍为亚音速。喷嘴扩散段产生激波后,由于熵的增加,式(1)、式(2)和式(5)不适用全部喷嘴。

进一步降低背压,如图2中⑥所示。此时,激波刚好出现在出口端面上。这种情况下,扩散段内不出现激波,且全部为超音速,满足pe=pb,及满足式(1)、式(2)和式(5)。从式(13)的解知,当喉部达到音速时,出口马赫数Mae有2个解,分别为图2中③和⑥所示曲线。

(14)

5.2 激波计算

假设喷嘴扩散段中产生的激波为正激波,且不考虑激波厚度。激波控制体(control volume,CV)如图3所示。

图3 喷嘴扩散段激波分析控制体Fig.3 Control volume for shock wave analysis of nozzle diffusion section

控制体CV基本方程,即:连续性方程、动量方程和热力学第一、第二定律方程,如以下式(15)所示[9,12]。

(15)

由式(15)可导出激波前、后的压力、温度和马赫数等参数:

(16)

式中下标u、d分别表示激波前、后参数。

y=1.087 3x-0.058 1

(17)

图4 激波前、后热工参数关系图Fig.4 Thermal parameters before and after shock

利用式(17)可以大大简化求解激波后压力。根据理想气体状态方程,可以导出激波前、后的气体密度关系式:

(18)

从图4知:1)激波后流动一定为亚音速;2)激波后温度高于激波产生前;3)激波后,压力间断性地急剧上升(平方关系);4)激波后的滞止压力小于喷嘴上游滞止压力。

6 数值模拟与实验验证

6.1 数值模拟验证

以A14喷嘴为模拟对象,对其进行建模和网格划分,建立二维柱坐标下的可压缩粘性气体的连续性方程、N-S方程、能量方程和气体状态方程,并引入标准k-ε模型与标准壁面函数法。[3]

在喷嘴入口条件加入p0=0.101 3 MPa的滞止压力;喷嘴出口条件加入pb=0.051 0 MPa的背压(同pe), 即背压比pb/p0=0.503。 模拟得到压力云

表1 激波前后的压力和马赫数Tab.1 Pressure and Ma before and after shock

图与速度云图如图5所示。从图中可以观察到,喷嘴喉部达到0.528临界压比;在离喉部下游约4.5 mm区域,云图均有突变,说明这个区域产生了激波。

图5 A14喷嘴背压比为0.503的压力、马赫数云图Fig.5 Pressure and Ma at BPR is 0.503

根据数值模拟数据,得到喷嘴轴线上的压力分布如图6所示。从模拟结果可以看到,在激波后,压力还经历1次波动。图6同时给出了一元流动理论计算结果,可以看到压力的变化趋势基本吻合(扩散段压力回升段最大误差约18%)。

图6 A4喷嘴压力沿轴线分布曲线数值模拟与理论计算比较(背压比0.503)Fig.6 Simulation and theoretical value of A4 mozzle pressure distribution curvealong the aixs

6.2 实验验证

文献[6]对1种二维缩放喷嘴(two-dimensional convergent-divergent nozzle)进行了实验研究。二维缩放喷嘴是1种由几段行线与宽度为101.3 mm的二维长方形结构的喷嘴,喷嘴的行线如图7所示。

图7 实验喷嘴的几何结构[6]Fig.7 Nozzle flap geometry for experiment[6]

本文针对以上二维缩放喷嘴,运用一元流动理论进行了计算,计算结果如图8和表2所示。

表2 本文与Craig A其它实验数据[6]比较Tab.2 Comparison between the calculated results based on 1D theory and other Craig A experimental data[6]

图8 一元流动理论计算结果与Craig A实验数据[6]对比Fig.8 Comparison between the calculated results based on 1D theory and Craig A experimental data

扩散段压力回升,一元流动理论计算结果均大于数值模拟和实验值。可能是一元流动模型未引入流动阻力和气体边界层影响,因此压力计算结果高于实际值。

7 总 结

本文阐述了背压比、临界压比、临界背压比等一些容易混淆的概念;从气体一元流动理论出发,从数学上证明并推导了实际条件下音速喷嘴的流量公式;从气体流动的基本方程出发,讨论了喷嘴扩散段中产生激波的机理,并对激波前后参数作了计算。一元流动理论计算和数值模拟均发现,在较大背压比范围内,或只要未达到设计条件,扩散段必产生激波,并伴随出现压力波动现象。由于扩散段中气体为亚音速流,因此,这种压力波动会向喷嘴上游传播,对于喷嘴的质量流量稳定是不利的。只有当背压比足够小,且达到设计条件:pb<(pe)min,这时,喷嘴扩散段中全部为超音速,喷嘴出口端面压力达到最小,且不再变化,下游侧的压力任何波动都不会向喷嘴上游传播。实验证明:此时,喷嘴流动参数不再有任何变化。

感谢上海理工大学黄伟民教授在论文撰写过程中给予的指导和帮助。