基于改进注意力机制的认知障碍病程分类

李梅梅, 胡春海, 周 影, 宋 昕

(1.燕山大学 电气工程学院,河北 秦皇岛 066004；2.东北大学 秦皇岛分校,河北 秦皇岛066000)

1 引 言

阿尔茨海默症(Alzheimer’s disease, AD)俗称老年痴呆,是发病进程缓慢、随时间不断恶化的神经退化性疾病,综合的发病概率占据痴呆症中的60%～70%,其真正成因至今尚不明确,且治疗费用昂贵。早期轻度认知功能障碍(early mild cognitive impairment, EMCI)是介于正常衰老(normal subject, NC)与AD之间的过度发展阶段,研究显示认知障碍(mild cognitive impairment, MCI)受试者以每年约10%～15%的速度发展为临床AD,如何对其予以早期精准诊断并进行正向干预是急需解决的问题。

随着电子医疗影像技术的进步和发展,作为目前最普遍的一种医学图像形式,磁共振图像(magnetic resonance imaging, MRI)能够清晰地显示所检测的软组织和结构形态,且对比于其它医疗图像成像方式,可避免对身体造成电离辐射的影响。而对阿尔茨海默症而言,MRI图像分析在反映AD和MCI患者脑组织萎缩情况有出色的表现。目前,越来越多的学者倾力于通过深度学习和大量医学图像数据相互结合对AD分类进行综合研究[1]。

近年来,很多学者以MRI和信息特征提取相结合为基础进行阿尔茨海默症的分类研究。文献[2]利用选择自编码算法对受试样本信息中提取正电子发射断层扫描(PET)、MRI、脑脊液检测(CSF)等数据特征,对AD和NC、MCI和NC以及AD和MCI进行二分类,达到较好的分类效果；文献[3]在研究中利用分类SAE对PET、MRI数据进行高度的信息特征提取,并将AD、pMCI、sMCI、NC之间进行四分类,分类的平均准确率达到46.3%的水平；文献[4]运用CNN特征学习的方法,对预先训练好的卷积模型进行了图像的特征提取,并在AD、MCI与NC分类中取得较好的结果；文献[5]提出了一种基于多尺度下皮层厚度差异的脑网络构建方法，该方法解决了网络构建中仅考虑脑区均值间关系而忽略脑区内局部特性的问题；文献[6]从MRI图像中提取AD相关区域的判别性图像块作为输入数据,利用3D-CNN进行训练,得到了91.09%(AD与NC)和76.90%(EMCI与LMCI)的准确率。

本文旨在提高计算机辅助诊断效率,同时促进疾病的病理生理机制研究。提出了基于改进SE(squeeze-and-excitation)模块二维双路径融合网络的分类方法。采用SE注意力模块,自动提取相关特征；结合双路径网络,构建特征图的差异性,利用特征图中区域差异性实现网络的不平衡关注,以实现网络性能的有效优化；鉴于样本图片四周信息少中心信息量大的特点,在网络中加入缩减系数模块,增加图片有用信息占比；对通道注意模块的权重函数设计,增大特征图间差异,联合二维双路径网络,增大网络倚重点,提升分类性能,减弱模型过拟合现象。

2 基于SE模块二维双路径融合网络

2.1 通道域注意力机制

通道域注意力机制[7～9],为每一个通道特征区域增加权重表达其所受关注度,其公式为：

(1)

通道注意力机制为图片产生的多个通道信号增加特有权重,该权重的大小与相关度成正比。SE模块可以模拟卷积神经网络(CNN)中特征图的通道,卷积后得到具有各通道特点的特征,使用SE模型可标定各特征通道权重。SE模块主要由挤压(squeeze),激励(excitation)和注意(attention)3部分组成。挤压函数对每个路径内的特征图进行全局平均池化操作，将每个通道用一个数值表示，公式见式(2)；激励函数是在得到sequeeze的通道表示后, 通过2层全连接层实现对每个通道的重要性进行预测,公式见式(3)；将SE模块获得的对应通道权值与通道值相乘, 实现依赖于尺度函数,有利于增强网络对关键通道域的注意力,公式见式(4)。

(2)

s=Fex(z,W)=σ(g(z,W))=σ(W2δ(W1Z))s

(3)

(4)

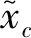
2.2 模型结构

深层次的网络有利于挖掘图像更多细节信息,但不利于训练,单一小卷积核造成冗余信息多等问题,对VGG16模型进行改进,本网络较VGG16减少后三层卷积,同时增加并行模块。图1所示网络模型的基本结构。

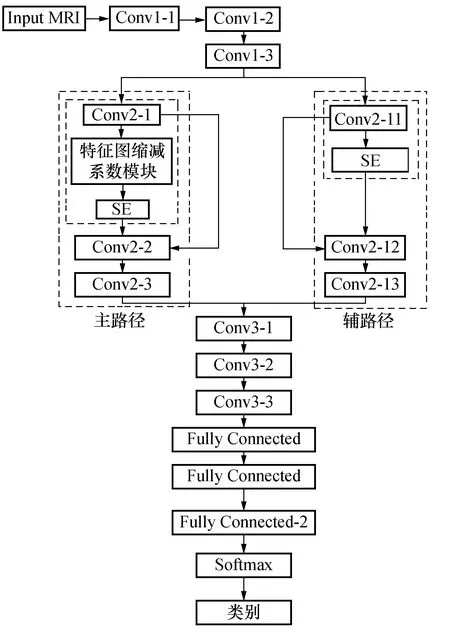
图1 SE模块二维双路径融合网络的模型结构图Fig.1 Model structure of SE module two dimensional dual path fusion network

如图1所示,网络中加入SE注意力模块,其中Conv2-11、Conv2-12和Conv2-13的卷积核大小为 5×5,其它卷积核大小为3×3。针对原始图像四周有用信息少,中心区域像素丰富的问题,采用大卷积核降低小卷积造成的冗余信息,同时采用valid方式,减少特征图周边无用信息,增加中心有用信息占比。本文将表1并行网络中由Conv2-11、Conv2-12和Conv2-13三卷积组成的路径称为辅路径,Conv2-1、Conv2-2和Conv2-3三个卷积组成路径称为主路径。

2.3 缩减系数模块及SE的嵌入方式

为减少冗余信息,在主路径中,将第一个卷积层输出特征图沿图像边缘切割,剪切系数为k。假设输入MRI图像的高度为Hin，从中裁剪的上边缘全黑像素高度为hin，输入模块的特征图高度为Hi，通过式(5)算得：

(5)

式(5)可分别计算AD、NC和EMCI三类数据所有样本的缩减系数。k的值由式(5)计算求得，为保留更多图像信息，由原始图像计算数据集的最大缩放系数k取值为8，若增大裁剪区间会裁减掉部分有用信息。为探讨k值变化对分类结果的影响，将k取整处理，其计算过程如下：

[Wo,Ho]=[k∶Wi-k,k∶Hi-k]

(6)

式中Wo和Ho表示经减模块计算后特征图的宽和高。

主路径中使用小卷积核,冗余信息较多,因此将经过主路径中的第一个卷积层的特征图进行压缩运算,将经过压缩系数模型的输出特征图作为SE模块的输入,输出权重与经过主路径的第一卷积输出特征图按通道相乘,作为第二卷积层的输入。在辅路径中,将卷积层的输出连接SE模块,即可获得通道权重系数,再与原特征图融合,形成第二个卷积层的输入。为放大中心有用信息占比,将主路径和辅路径的最终输出特征进行相加融合,辅路径中使用较大卷积核,最终输出特征图居中且比主路径中输出特征图小,因此为方便后续进行特征融合,在辅路径输出特征图融合前加入zeropadding层。

主路径中Conv2-1输入尺寸为m×n,通道c的特征图为x,经缩减系数后的尺寸为m1×n1,通道c1的特征图为x1,以及通过SE模块的输入长度为1×1,通道数为c1的权重图M(x1)；M(x1)在每一条通道处的取值为F(i)(x1),M(x1)和F(i)(x1)结合方式见式(7)：

F(o)(x1)=M(x1)·Fn(i)(x1)

n=1,2,3,…,c1

(7)

式中:k表示通道数;F(o)(x1)代表下一层卷积层输入。

3 通道注意模块的权重函数设计

设计类激活映射(class activation mapping, CAM)中全局平均池化层的权重计算函数(new meight module, NW),并将其添加到网络中。同时,最后一层卷积后增加CAM中最大池化计算权重层(max pooling weight layer, MPW),用以观察整个网络特征变化,提高分类性能。

3.1 权重函数设计

对特征图进行全局平局池化操作后输入2层的神经网络。此时,得到1×1×C主通路的权重张量,其中C为通道数。辅路第一卷积层的输出特征图作为CAM中平均池化层的输入,得到1×1×C辅路的权重张量。

为弥补2分支网络单独使用的缺陷,同时,为找出差异显著且信息量显著的特征图,对2通路的权重张量做以下处理：

(1)当数据量较大时,避免权重相同或者极度接近的情况,对2个张量做差处理,为避免出现负权重,对做差后的值进行加绝对值操作,如式(8)所示。其中,X1为主路径输出权重值大小,X2为辅路径输出权重值大小；

Fabs=|X1-X2|

(8)

(2)由于本文对图片均进行归一化处理,导致系数均介于0～1之间,因此对Fabs进行指数处理,使得所有权重值大于1,如式(9)所示。

X=eFabs

(9)

(3)将所获得的权重分别与主路径的第2层卷积层的输出特征图及辅通路的第2层卷积层的输出特征图按照通道相乘再相加,做为下一级输入。

3.2 权重函数的嵌入方式

NW模块内部结构如图2虚线部分所示,每条路径均进行全局平均,并对2支路进行权重函数设计。NW模块、MPW模块及缩减系数模块嵌入方式见图3。图3中虚线区域为两条路径,左支为主路径,将此模块的输出作为NW模块的输入；右支为未加入缩减系数模块的辅路径。2条路径均通过全局平均池化操作,获取各通道权重系数。将最终得到的权重值与2条路径中的第2层卷积输出特征图按通道相乘,再相加融合,即为权重函数的嵌入过程。在辅路径输出特征图融合前加入zeropadding层,方便后续特征融合。

图4为MPW模块内部结构。网络层数较多,更深层次的语义信息增多。因此,首先将MPW模块嵌入全连接层前,使得网络中最后一个最大池化层的输出特征图为MPW模型的输入,以获取权重；再将最后一个最大池化层的输出特征图按通道相乘,做为全连接层的输入。

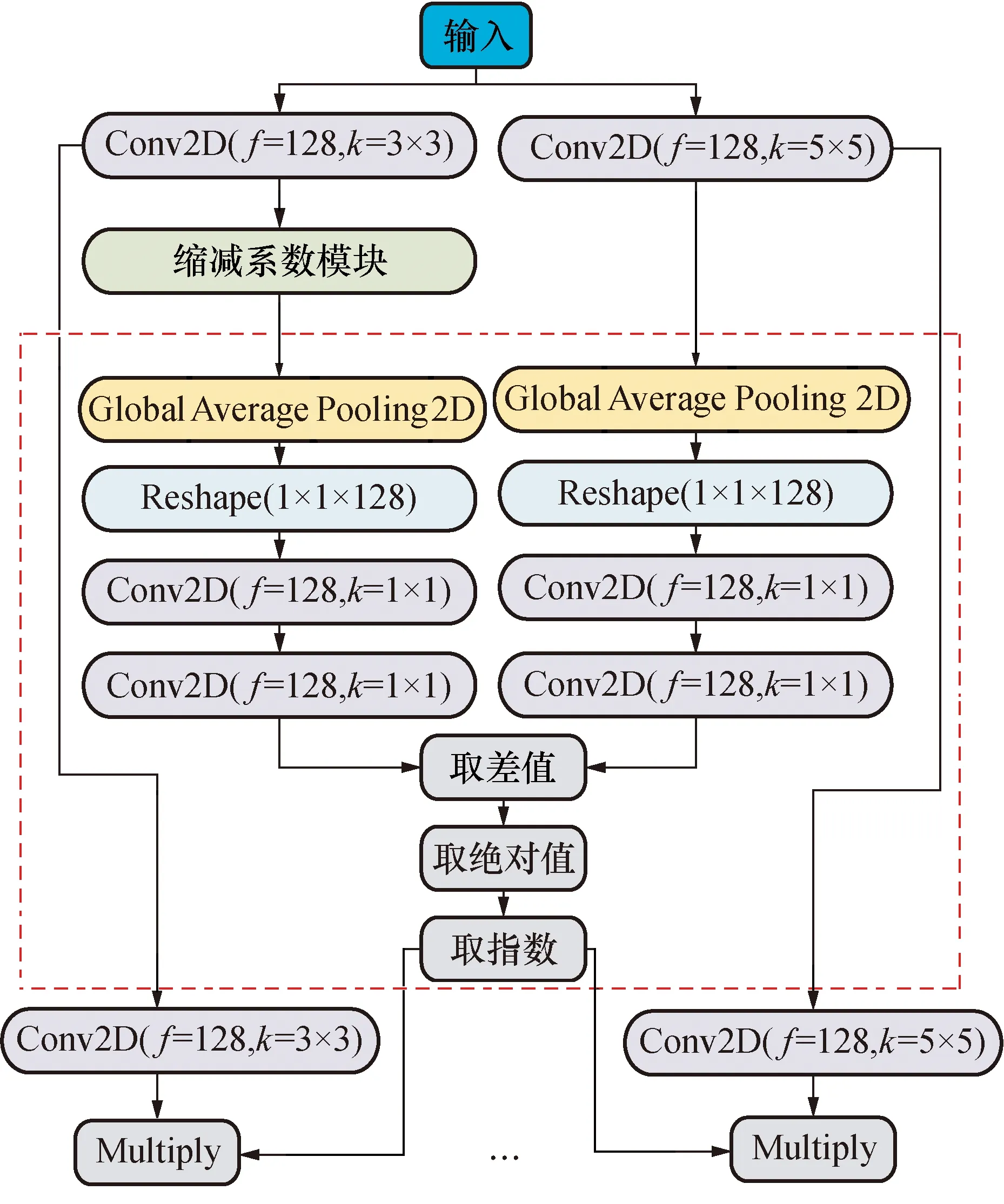
图2 NW模块内部结构图Fig.2 Internal structure diagram of NW module

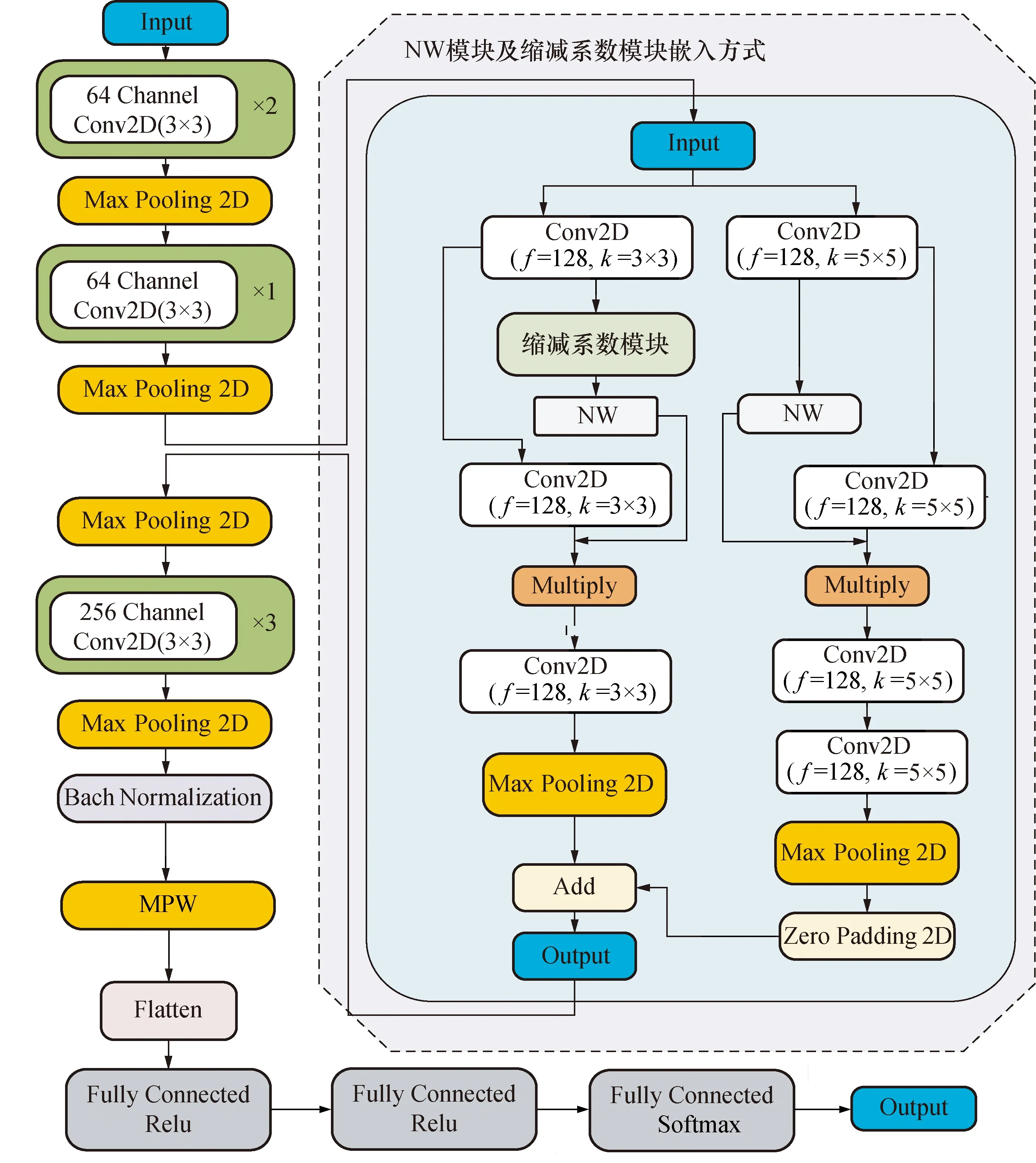
图3 NW模块、MPW模块及缩减系数模块嵌入方式Fig.3 NW module、MPW module and scaling factor module embedding method

图4 MPW模块内部结构Fig.4 Internal structure diagram of MPW module

4 实验及结果分析

4.1 数据获取

本文实验所用的T1加权图像来自于ADNI数据库[10,11],共选择329个ADNI样本作为本实验数据。如表1所示该数据集共包含110位患病样本(AD)、109位早期轻度认知障碍(EMCI)和110位正常样本(NC)。为尽可能展现海马体位置,实验中沿冠状面进行切片,并按照6:2:2的比例划分训练集,验证集和测试集。

表1 样本基本信息表Tab.1 Table of basic information about the sample

4.2 实验方法

实验所用设备为带有Titan X GPU的系统,主机运行系统为Ubuntu 16.04。学习架构为Tensor Flow 2.0。图像预处理部分包括头动矫正、配准、颅骨剔除、图像增强和分割等步骤[12]。同时每类样本均进行归一化处理,以此减轻后续网络训练负担。图5为本文实验流程图。

图5 本文方法实验流程图Fig.5 The flow chart of the experiment of this paper

4.2.1 AD vs. EMCI分类任务

调节缩减系数模块参数可提升特征图中有用信息占比,减少卷积后产生的冗余信息。在网络中加入缩减系数模块,k值为2、5、7、8的4种情形下,对AD和EMCI进行分类并评估网络性能。

在本实验中,学习率设定为0.7×10-4。每个模型完成200个epoch的训练,并将batch size设置为128。表2展示了4种k值测试集的分类结果。图6为AD与EMCI四种情况下验证集的ROC曲线。

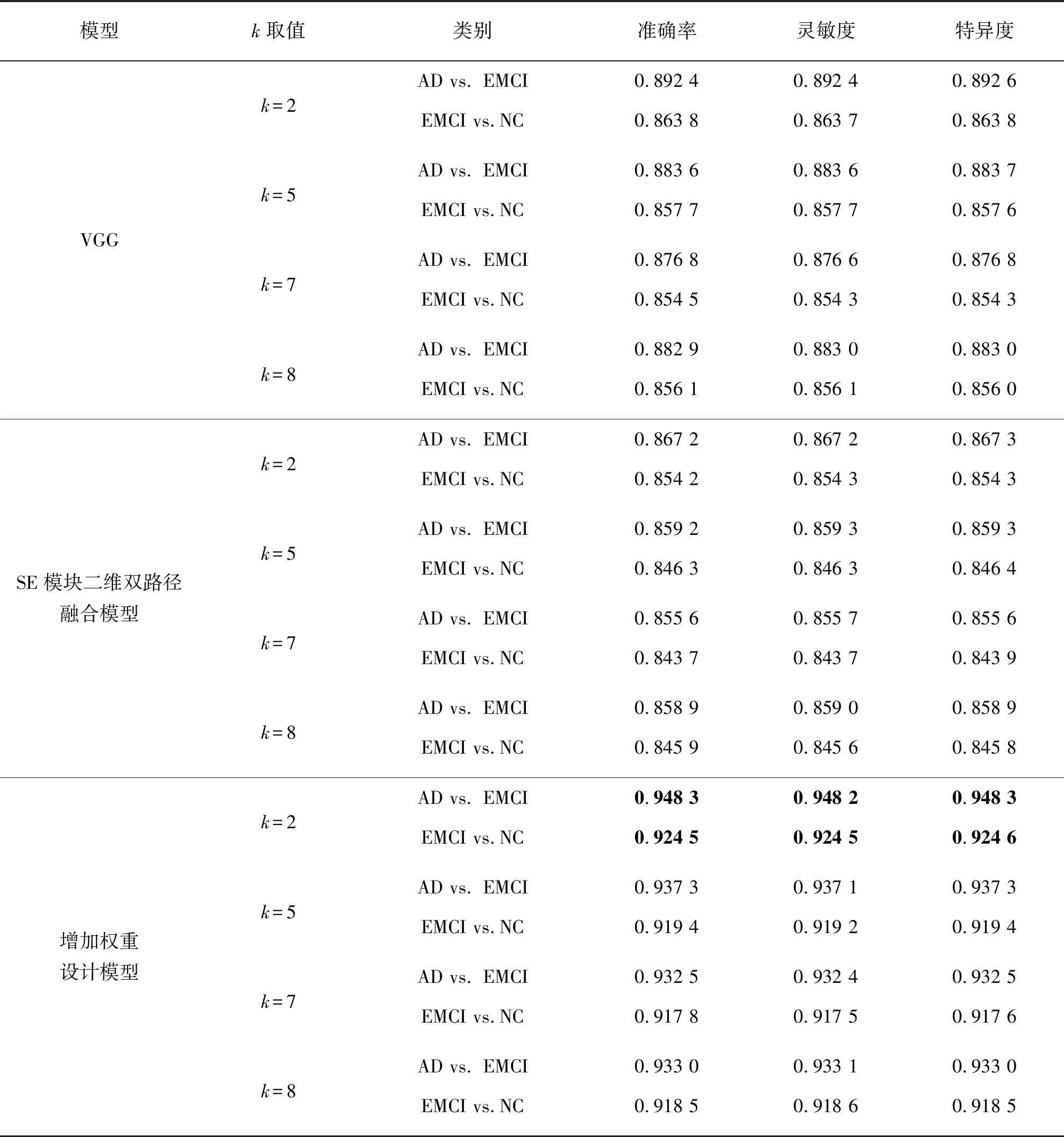
表2 3个模型测试集分类结果Tab.4 Classification results for the three model test sets

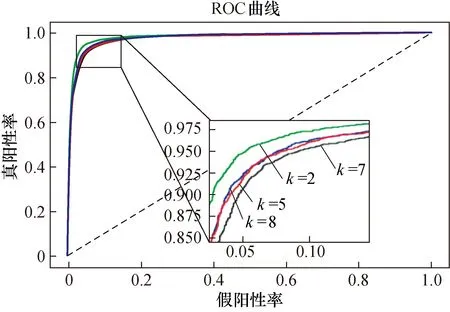
图6 AD vs. EMCI四种模型的ROC曲线图。Fig.6 ROC curves of the four AD vs. EMCI models.

为更加直观地表示模型4在个参数下的分类效果,图7分别比较了4种情形下分类模型在验证集上的准确性、灵敏度和特异性结果,横坐标的取值范围为[1～9],间隔为1,纵坐标的取值范围为[0.93～0.95],间距为0.01。

4.2.2 NC vs. EMCI分类任务

对NC和EMCI分类中采用k值不同进行上4次试验,试验中,学习率设置为0.7×10-5。对每个模型进行200个epoch的训练,并将batch size设置为128,其中测试结果如表2所示。

在辅路径中卷积拥有较大的卷积核,而大卷积核会丢失较多信息,因此,未加入缩减系数模块,输出实数的权值不会随k值的变化而变化。而在MP中,使用小卷积核,这会使得冗余信息增多,因此,该路径中加入缩减系数模块,随着k值的增大,有用信息在特征图中心的比例增大,使得MP输出的实际权值增大,即X2的值增大。因此如图7和8所示,随着k值的增加,2种分类任务的准确率均呈现先下降后上升的趋势。

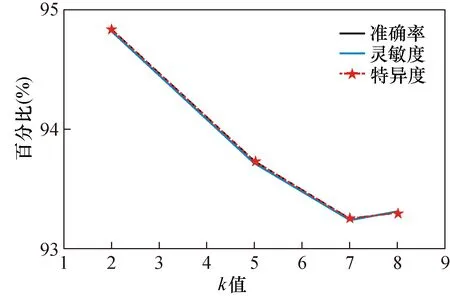
图7 ADvs.EMCI四种情况下结果趋势图Fig.7 Results trend chart of AD vs. EMCI in four cases

4.3 实验结果分析

本文分别对改进的网络模型、SE模块二维双路径融合模型以及VGG模型进行AD,EMCI和NC二分类。在AD vs. EMCI和NC vs. EMCI分类任务中,如表2所示,将加入权重设计后的模型与VGG16模型及基于SE模块二维双路径融合模型分类结果比较。当k值为2时,增加权重设计的SE模块二维双路径融合模型其AD vs. EMCI分类准确率为0.948 3,NC vs. EMCI分类准确率为0.924。

图9显示了AD vs. EMCI分类中3种模型下的准确率对比折线图。可以看出,增加权重设计的模型在k值为2时分类准确率，相较于SE模块二维双路径融合模型和VGG模型分别提高了8.11%和5.59%。

图8 NCvs.EMCI四种情况下结果趋势图Fig.8 Results trend chart of NC vs. EMCI in four cases

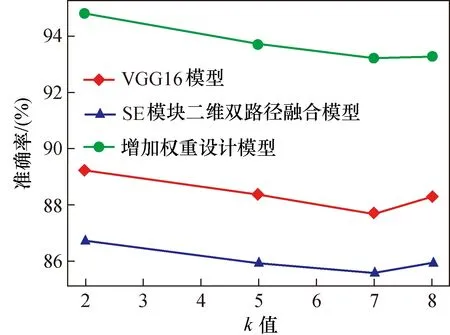
图9 3种模型的精度对比折线图Fig.9 Line chart of accuracy under three models

同时为验证所提出方法的优越性,将本文提出的改进网络模型与现有先进方法进行对比,表3中其它模型数据集均采用ADNI,由于NC vs. EMCI分类更具有临床意义,因此,表3仅对该组分类结果进行对比分析。本文提出的方法准确度远高于其它先进方法。

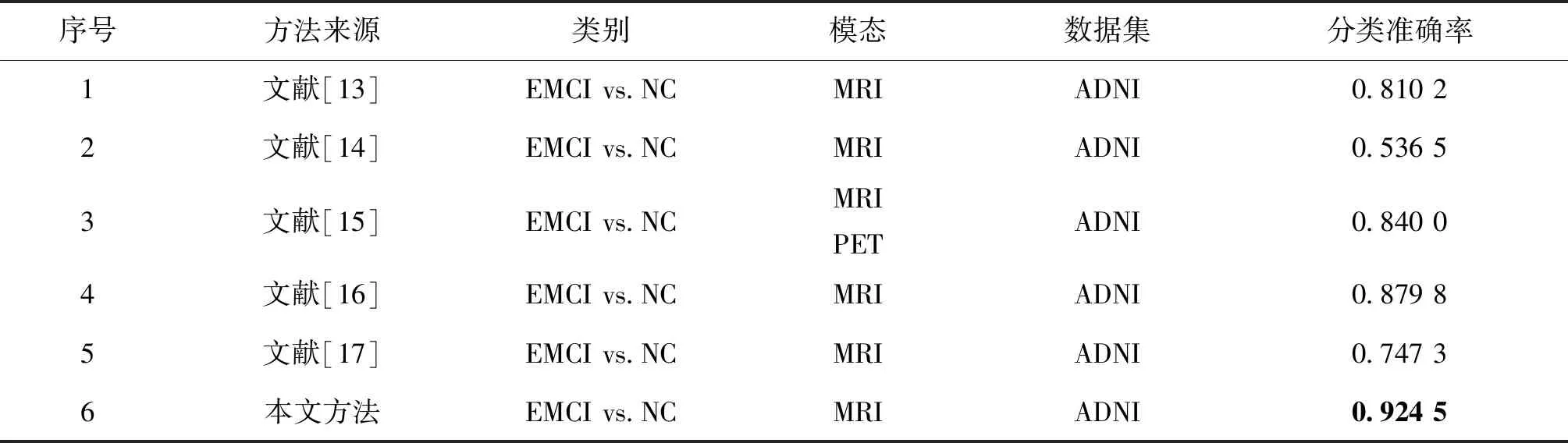
表3 近5年多种方法EMCI vs.NC分类准确率对比结果Tab.3 Comparative results of EMCI vs.NC classification accuracy of various methods in recent five years

6 总 结

本文针对早期阿尔茨海默病患者大脑病变程度较轻,导致分类效果差的问题,提出了基于SE模块的二维双路径融合网络模型,同时提出了权重函数设计算法,通过构建通道注意模块的权重函数,增大特征图差异,提高权重差距,联合二维双路径网络,增大网络倚重点,以实现网络性能的优化。与现有方法对比,所提出改进的网络模型在阿尔茨海默病的早期分类中达到更高的指标,有效证明改进网络性能的可行性。