整合·关联·逆向：初中数学结构化复习的设计与思考——以“一次函数”单元复习课为例

吴玥霞

(浙江省桐乡市求是实验中学 314500)

复习课的目的是温故知新，融会贯通.《浙江省中小学学科教学建议》案例解读指出：复习课要根据学生的认知特点和规律，通过对已学知识的系统回顾，建构完整的知识结构，优化认知结构；在问题的解决过程中，运用分析、讨论、归纳、总结等过程，优化解题方法，提高解题能力，适当渗透数学思想方法，有效发展学生的数学思维能力.

1 审视教学常态，复习设计缺乏结构化思考

1.1 学习材料的确定缺乏精准性

学习材料是数学复习教学的重要资源和活动载体.结构关联的学习材料，容易让学生主动建构认知结构体系.然而部分教师对学习材料的选取较为随意，未加筛选、重组与整合，直接拿来使用，对教材整体的编排意图理解不到位，对学生的真实学情了解不清楚，对学习目标的确定不精准，导致“理”(梳理)不到位、“练”不具针对性、“测”无及时反馈.

1.2 学习内容的设计缺乏整体性

学习内容的设计是学生学习活动的重要保证.整体关联的内容设计，能使学生的学习过程形成一个稳定的认知结构.然而部分教师对认知结构的理解不够全面，忽视知识的整体性、内在的关联性以及对内容理解的深刻性，使得教学呈现点状化、碎片化、狭窄化的零散现象，导致学生难以形成学科的“整体观念”，常常出现知识遗忘率高、基础不扎实、解决综合题的能力薄弱、学习的迁移度低等问题.

1.3 评价任务的设计缺乏过程性

学习评价是对学生学习效果进行的价值判断.多维实证的评价设计，能让学生在意义建构的过程中调节好学的精度，促进数学素养的提升.然而部分教师只注重知识和技能的评价，而忽视了三维目标要求下形成的知识结构、方法结构、思维结构的评价点.这种限于“浅层学习”的单一评价，导致学生难以获得对学科的本质理解，难以实现知识的应用迁移.

针对以上现实情况，教师要着眼于知识关联，着力于数学思维，着重于学习能力，通过结构化教学培养学生的数学核心素养，这是数学复习教学的应然之举[1].

2 回归教学本源，复习设计建构结构化路径

数学学科本质是让学生理解数学概念、把握数学思想、感悟数学思维、追求数学理性精神.数学教学须回归学科本质，而结构化教学是一种新的教学视角，是一种回归本源的教学实践[1].复习设计以结构化理论为方法论，以构建结构化学习为目的，以课程目标为指引，遵循数学学科的结构特质，把握知识内在逻辑关联，通过对学习材料的整合设计、学习活动的关联设计、评价任务的逆向设计，让学生在自主活动中进行有意义的建构，从而实现层级目标结构化、知识(包含过程、方法、思想)结构化、评价任务结构化，逐步形成结构化复习设计的基本范式，发展学生结构性思维，提升学生的数学素养(图1).

图1 初中数学结构化复习设计路径图

3 立足实践架构，复习设计蕴涵结构化策略

“结构化”包含两层含义，即结构化教学和结构化思维，前者是手段和路径，后者是目标和价值取向(图2)[2].在实践层面，复习设计构建“整合·关联·逆向”三个环节，整合是前提，关联是关键，逆向是保障.通过实施内容材料结构化、教学进程结构化和评价输出结构化等策略，让学生经历“理解(隐性思维显性化)→重构(显性思维结构化)→呈现(结构化思维形象化)”的思维过程，实现数学思维从零散状向结构化的转化[2]，从而形成“设计—实施—评价—改进”的教学活动闭环.接下来本文结合“一次函数”的章节复习课，来阐述结构化的复习设计策略.

图2 结构化策略图

3.1 学习材料的整合设计

学习材料的整合设计是指在适切的目标指引下，使学习材料设计从“零碎”走向“整合”.可以通过“明晰—研判—统整”这一路径设计复习学习材料(图3).

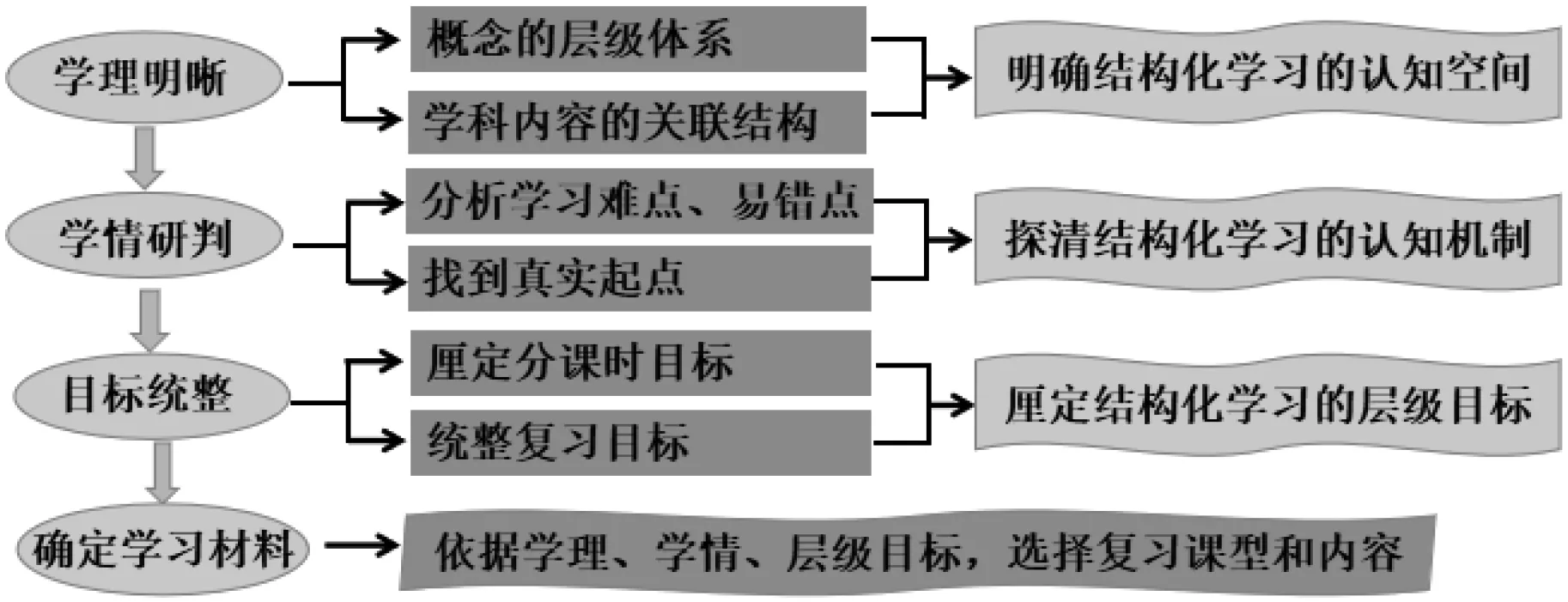
图3 学习材料的“整合”设计策略图

3.1.1学理明晰——明确结构化学习的认知空间

解读教材要着眼于数学整体知识结构的建构，将零碎的知识“嵌入”到“单元”视野之中，通过对课时内容与本单元、本领域、相关领域和学科外内容的关联性结构分析[3]，梳理分析概念层级体系，理解概念、单元、大概念的横向和纵向的知识结构网，明晰结构化学习的认知空间.

函数是初中数学的重要内容，属于“数与代数”领域，而一次函数是学生初中阶段学习的第一类具体函数，是函数的特例，具有函数的通性，为后续学习其他类型函数提供研究思路和方法.因此在进行复习设计时，须对本章教材内容、知识结构进行关联分析和梳理(图4).

图4 “一次函数”整章知识结构图

3.1.2学情研判——探清结构化学习的认知机制

分析研判学生在学习过程中存在的知识难点、困惑点以及易错点，找到复习学习的真实起点，弄清学生的相异构想，突出以生为本.

从一次函数的学习过程来看，学生对一次函数、正比例函数的表达式以及待定系数法、函数图象的画法掌握较好，但是对一次函数表达式中k，b的理解，性质的简单应用以及与图形类、生活类结合的综合应用，学生感觉难度很大，出现的错误也较多.

3.1.3目标统整——厘定结构化学习的层级目标

厘定章节的分课时目标，将一个个的“小目标”融合到单元目标，把一个单元知识层面上“知道”、思维层面上“理解”、技能层面上“操作”进行统整.然后根据学理和学情精准设定大概念下的复习分层目标.在制定目标时，将内容结构、方法结构、素养结构融入目标结构之中，形成层级式目标结构图，见表1.

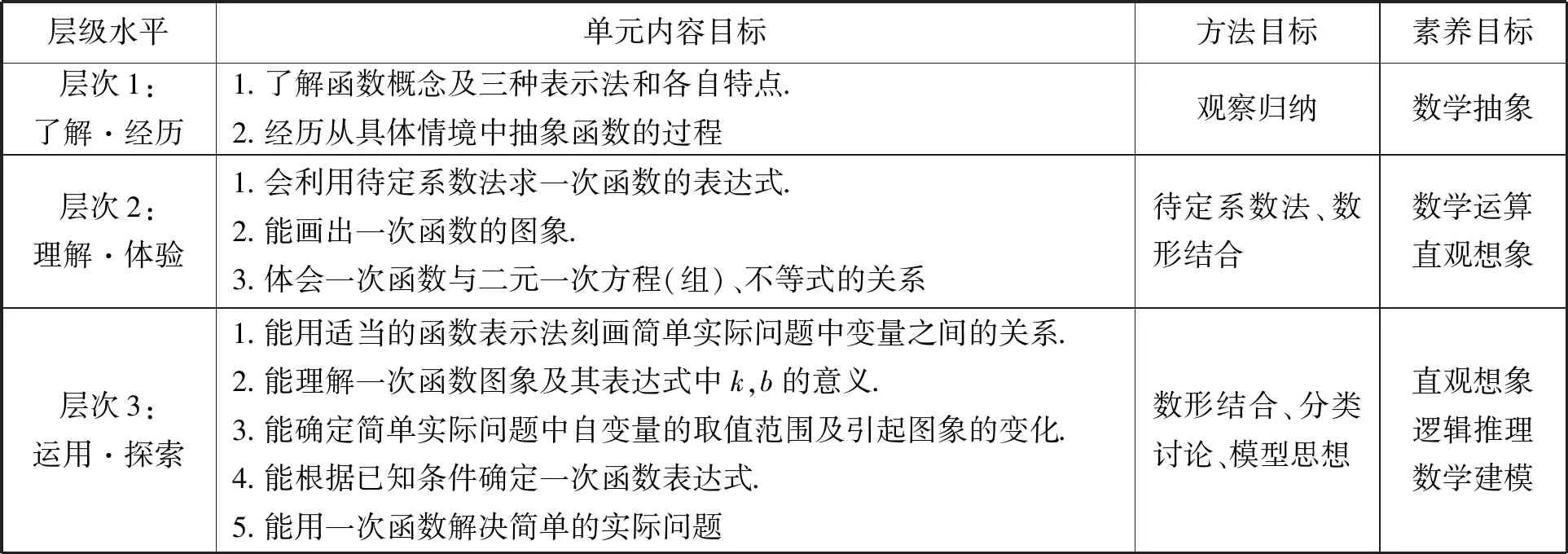
表1 “一次函数”单元复习层级目标

3.1.4学习材料的确定

依据层级式目标，拟定复习课型(基础复习课、专题复习课)和主题内容，然后寻找与之相适应的复习材料.

根据以上三方面的分析，一次函数单元复习设置1节基础复习、2节专题复习，见表2.

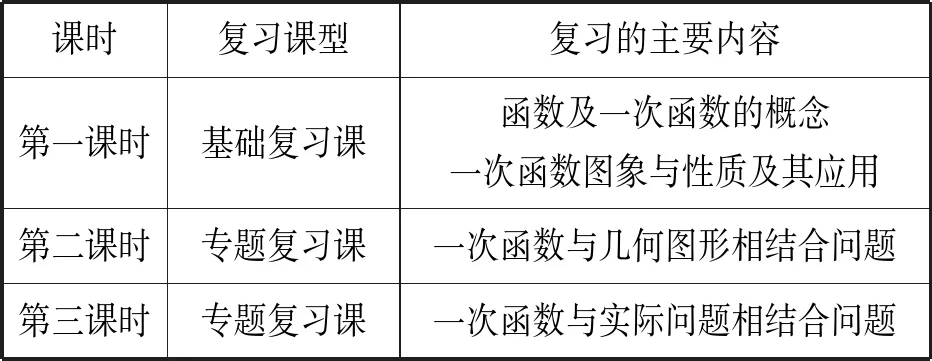
表2 “一次函数”单元复习课设置情况

3.2 学习活动的关联设计

学习活动的关联设计是指基于知识结构、认知结构，围绕思维结构为核心的素养结构发展目标，设计学的结构、教的结构、素养结构，使学习活

动从割裂走向关联.横向上通过“驱动—关联—提炼”三个递进序列，纵向上通过“问题—活动—方法”三个平行要素得以实现(图5).

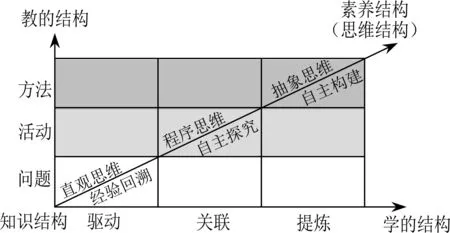
图5 学习活动的“关联”设计策略

3.2.1问题驱动——形成研究系列

问题引领是以核心问题、基本问题、问题串等作为学习内容，解决的是学什么；“问题驱动”在核心问题的驱动下，解决怎么教.教师可以把问题融入情境中，依据情境知识设计连续、递进的子问题串，让学生在直观感知的思维状态下，激活原有的知识经验，使研究逐步走向深入，形成研究序列.

如笔者的公开课“‘一次函数’单元复习课”第一课时，问题设计如下．

探究1已知一次函数y=(m+2)x+3-n满足以下条件，分别求m,n的值．

问题1：它是正比例函数？

为了帮学生打开思路，教师呈现了问题1，接下去就让学生根据已有学习经验和知识积累来提问.于是，学生纷纷提出如下一些问题：

问题2：它是一次函数吗？

问题3：它的图象与y轴的交点在x轴的下方吗？

问题4：它的图象经过第一、二、三象限吗？

问题5：它的图象不经过第四象限吗？

问题6：它的图象与直线y=2x+1平行吗？

问题7：它的图象经过(0，3)和(2，2)吗？

……

探究2把以上问题解决后，针对问题情境7得到的函数解析式，继续启发学生思考：又可以设计哪些问题呢？

生1：可以求与x轴的交点坐标和与y轴的交点坐标.

生2：可以求与坐标轴围成的三角形面积.

生3：可以求两个交点之间的距离.

生4：可以设计求取值范围的问题.

生5：可以设计不等式的问题.

……

探究3为了进一步拓宽学生思维，笔者又在以上题目的基础上，生成以下3个问题：

问题1：若点P(x，y)是线段AB上的一个动点(不与A，B重合)，设△OPA的面积为S.求S关于x的函数解析式.

问题2：请你画出S关于x的函数图象.

问题3：在直线AB上是否存在点OP，使直线OP把△AOB分成面积相等的两部分？如能，请求出OP的解析式；如不能，请说明理由.

通过这样的问题设计，使学生了解知识点之间的横纵联系，加深对知识的理解，进一步完善了知识结构，提高其数学能力.学生不但领略知识解决的全过程，承担起问题解决者的角色，而且还总结问题，了解怎样围绕知识点出题.笔者始终认为教师也应该引导学生揣摩题目是如何设计的，而不是仅仅强化学生如何解题.

3.2.2活动关联——着力自主构建

弗兰登塔尔将数学学习活动概括为“数学化”，即将实际问题抽象为数学问题、数学问题符号化、数学原理形式化、数学理论应用化.教师结合复习学习材料，通过设计关联性的学习活动，凸显知识情境与核心元素的关联，建立知识表征与思想方法的关联，注重知识过程与工具创造的关联[4]，自主构建数学知识之间的逻辑链条，实现数学内部结构的系统化.

如笔者的公开课“‘一次函数’单元复习课”第一课时，活动设计如下(表3)：

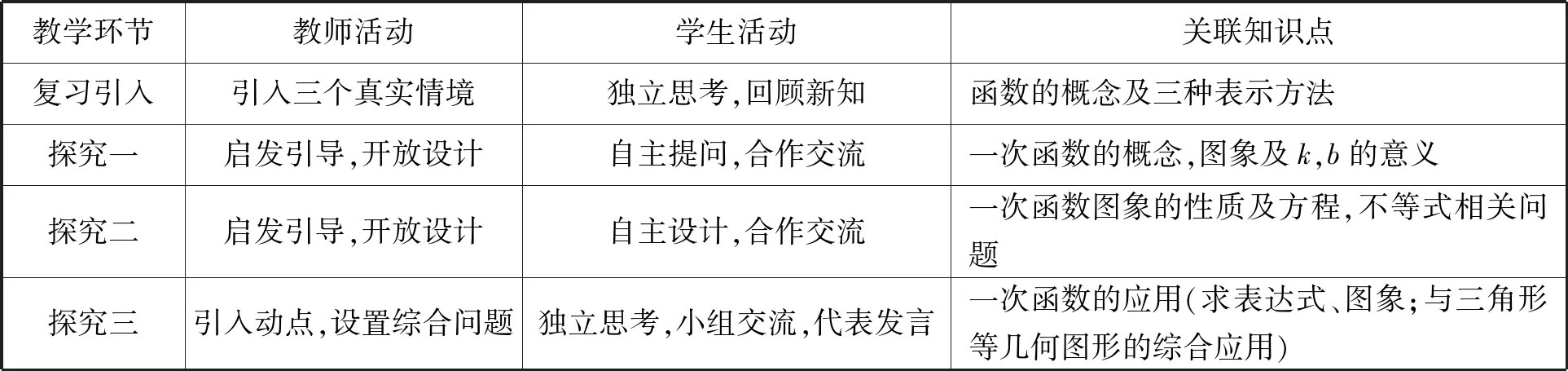
表3 “一次函数”单元复习课第一课时活动设计

通过设计关联性的学习活动，把复习材料经过“数学组织化”“逻辑的组织化”，在学习过程中不断引导学生实现知识点、线、面、体的多向关联(横向、纵向、横纵向)，从而感悟单元学习路径，生长出新的数学认知结构.

3.2.3方法提炼——发展结构思维

数学方法指在数学问题解决过程中所采取的步骤、程序和实施办法，是数学思想的表现形式和得以实现的手段.在具体内容的学习过程中，适时对数学思想方法及知识形成的过程结构加以归结、梳理.在建构知识体系的同时，思想方法也得到内化，促进结构化思维发展.通过创建结构化的学习活动，实现思维可视化，创新学习路径，帮助学生在大脑中形成结构功能良好、迁移能力强的认知结构.

一次函数与后续学习的函数有着相同的研究方法和研究过程，因此在“‘一次函数’单元复习”第一课时进行方法提炼时要做好以下三方面：

(1)知识内容方法的结构化(表4)

(2)单元学习路径的结构化

一次函数的单元学习路径：生活事实—函数概念—一次函数的概念—一次函数的图象—一次函数的性质—一次函数的应用

(3)数学思想方法的结构化

生活事实—函数概念：通过观察、分析、归纳等数学方法抽象得出概念；

函数—一次函数：从一般到特殊的研究方法；

一次函数的图象—性质：数形结合、从特殊到一般的研究方法得出性质；

一次函数的性质—应用：类比、迁移、转化，其中蕴含着函数思想、方程思想等.

3.3 评价任务的逆向设计

评价任务的“逆向”设计是指评价设计先于学习活动设计.评价任务的设计必须与目标相匹配，重点关注学生在学习过程中表现出来的知识结构、认知结构和思维结构，实现学习与评价同步，使得评价从“估计”走向“实证”.可以借助SOLO体系结构和结构化学习评价框架，通过“循环—介入—分析”这一路径实现.

3.3.1练测循环——助推核心素养发展

循环，即递进、上升，包括知识学习的方法、思想、情感、价值等循环.学生到底会不会学，学到什么程度，可以通过“练”这个环节来检测.通过不断循环练测，加深理解、促进内化、拓宽视野、增进知识以及认知、思维、素养等结构的完善与发展.

如在“‘一次函数’单元复习”第一课时，复习到探究一中问题6的环节时，教师及时让学生总结“在同一平面直角坐标系中，直线y=kx+b与直线y=mx+n的位置关系有哪几种，需满足什么条件?”之后，教师出示下面两题：

(1)直线y1=2x-1与直线y2=-x+5的交点坐标为，当x满足时，y1

A.相交 B. 平行 C. 重合 D.无法判断

3.3.2量表介入——精准评价学习活动

依据评价标准开发结构化学习的表现性评价表，包括评价的维度、评价的内容、学习表现等.评价维度分知识结构、认知结构和思维结构，分别对应的评价内容一是数学的概念、知识的记忆、理解和概括、应用等，二是学生的认知发展水平和数学认知结构，三是学生的思维水平和学科素养[4].学习表现分为A优秀、B良好、C合格.然后根据学生课堂的表现来评价目标的达成度，对学生的学习进行定性和定量评价(表5).

表5 “‘一次函数’单元复习”第一课时学习表现性评价表

3.3.3评价分析——调节学评优化学教

通过对学习过程中的表现观察评价和学生学习结果的多元评价，教师对照评价标准，开展定量和定性相结合的分析评价，综合分析学生在学习过程中的知识建构情况、认知结构的完善情况和结构化思维的发展情况.

综上所述，单元复习教学需要教师从数学学科的整体系统性、结构关联性的本质特征出发，通过对学习材料的整合设计、学习活动的关联设计、评价任务的逆向设计，让学生以整体关联的结构化学习任务为驱动，经历结构化的创造性学习活动，自主建构知识结构体系，促进结构性思维的发展，促使核心素养的提升.