基于化归思想的高中数学课堂教学思考

马海燕

⦿新疆乌鲁木齐市兵团第二中学

化归思想是处理数学问题的重要策略，其能化复杂为简单、化未知为已知、化非常规为常规，从而获得解决问题的思路.在高中数学教学中，教师要灵活运用化归思想，将问题从高维转化成低维，促使学生更好地理解和解答问题，加深学生对问题的认识，增强学生的思维能力.

1 基于化归思想的高中数学课堂教学策略

1.1 深挖教材内容，巩固基础知识

教师在培养学生化归思想时，应从教材入手，对教材中的定义、公式、例题进行分析，让学生明白化归思想的来源以及如何体现.教师在备课中，应对教材中的基础内容进行细化，让学生在初次接触新知识时能将新旧知识联系起来，将思想从旧章节平稳过渡到新章节中，实现思想上的转化.运用化归思想要以扎实的基础知识为前提.教师一定要让学生先将每一个章节的知识吃透，这样才能在不断吸收新知识的过程中保持思路畅通.

1.2 注重思想引导，培养探究兴趣

教师可以结合一些经典案例来引导学生运用化归思想，归纳法是高中数学中常用的解题办法，运用该方法时只需要观察简单的样本就可以推导出复杂的规律，适用于解决复杂问题，教师可以在归纳法教学中让学生接受化归思想.例如，“摸球问题”是经典的数学问题，在纸箱中装入2个白球、3个黑球，然后列举出可能出现的情况.对于这一问题的解决，穷举法显然是缺乏代表性的，数学归纳法更加适用.在解决问题后，教师可以询问学生：归纳法与穷举法有什么区别？如果样本数量不断扩大，还能用穷举法吗？这样就强化了学生对化归思想的认识和认可.化归思想使学生有了自主探究的可能，教师在应用化归思想时，应引导学生打开自己的思路对问题进行转化，灵活运用所学知识，这样就给了学生很大的自主发挥空间，培养了学生主动探究的兴趣.

1.3 把握化归原则，避免生搬硬套

运用化归思想应遵循以下几个原则：一要确保化归的规范性与有效性，应用化归方法必须有明确的对象、设计好的目标和合适的方法，解题时必须紧盯化归目标，盲目的化归只会走入死胡同；二要确保逻辑上的正确性和转化的等价性，转化时的前因后果应是必要的、充分的，转化后的结果应是原题的结果；三是设计合理的转化方案，实现同一转化目标可能需要采取多种转化方法，简捷合理的转化方案是必要的，但要避免生搬硬套.

2 化归思想的应用实践

2.1 数形转化

数与形的互相转化是高中数学的重要知识，也被称为数形结合思想.在数形转化中，学生可以利用几何知识来解决代数问题，或借助数量关系来研究几何图形的性质.几何与代数的结合，成为高中数学中的重要一面，这也体现了化归思想.

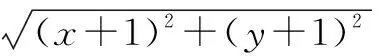
分析：这道题从表面上看是关于数的问题，但实际上却与“形”密切相关.在求解时，可以将原问题视为求点(x,y)到点(-1,1)的距离，即求点(x,y)到直线x+y+1=0的距离.到了这一步，学生即可通过其熟悉的点到直线的距离公式求得答案.

在这一问题的处理中，巧妙地对题干进行了转化，把代数问题转化成了平面几何问题，这样做的好处就是避开求最值时要考虑条件的满足等问题，简化了解题过程，降低了解题难度.同时，例1的难度较低，从这样基础性的数形转化思想入手，可以逐步培养学生的化归思想，为后续学习打下良好的基础.

2.2 正反转化

正反转化即当从正面入手解决问题的难度较大时，不妨从问题的反面进行考虑，通过求补集的方式逆向解决原问题.灵活运用正反转化可以解决很多难题.正反转化最常见的就是空间几何问题，如物体的空间截图、运动轨迹等，把三维空间问题转化成二维平面问题，利用平面几何的公式、定理、定义把待求解的问题不断简化，可以有效降低解题难度.

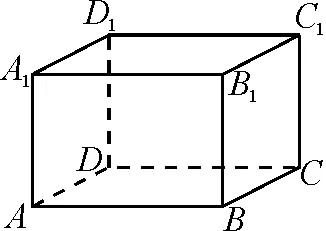
图1

例2在长方体ABCD-A1B1C1D1中(如图1)，已知AB=a,BC=b,AA1=c，且a>b>c.现有一物体从A点出发，沿着长方体ABCD-A1B1C1D1的表面运动到C1，求物体在运动过程中的最短路程.

分析：在这道题目中，可以将长方体ABCD-A1B1C1D1视为正六面体，将最右侧平面BCC1B1与最后侧平面CDD1C1展开，得到两个俯视图(图2和图3).通过平面几何中两点之间线段最短原理可以求出最短的路程是|AC1|，|AC1′|，|AC1″|之一.

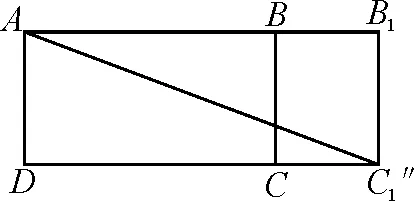
图2

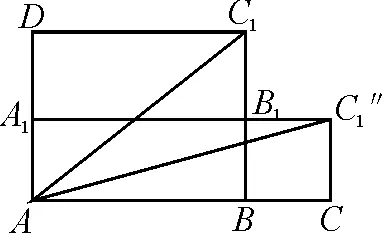
图3

最值问题的解答，通常需要转化成函数，但这道题目是空间几何问题，题干也没有给出函数式，所以转化成函数是不可取的.平面几何求最值的方法比较多，因此通过化归思想可以简化成二维平面问题，简化解答步骤.

2.3 一般与特殊转化

一般与特殊之间的转化既可以是从一般途径寻求解决特殊问题的方法，也可以是从特殊情况入手解决共性问题.

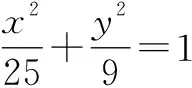
分析：在这道题目中，点B是运动的，因此很难直接得出sinA，sinC，sinB的精确值，但可以将这个一般性的问题特殊化，如将点B放到椭圆短轴的顶点，这样就可以利用正弦定理来解答问题.

2.4 局部向整体转化

对较复杂的数学问题，可以从总体上去把握.

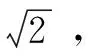
综上，高中数学教学中有大量可以应用化归思想解决的问题，教师在教学中应把握好转化的切入点，引导学生将困难问题简单化，使学生不但解决问题，更要掌握解决问题的思路.

3 结语

应用化归思想解答数学问题可以有效降低解题难度，为学生打开新的解题思路.教师在教学中应注意巩固学生的知识基础，为应用化归思想做好知识积累，并对化归思想在不同知识点中的应用方法进行探索，改善课堂教学质量，最终提升学生的解题准确率.