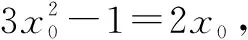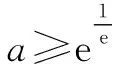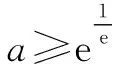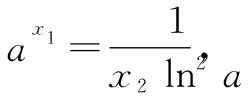基于思维导图的高考试题解法研究——2022全国甲卷文科数学第20题的探究

代锦春

⦿云南师范大学附属世纪金源学校

代红军

⦿昆明市官渡区第六中学

朱俊霖

⦿西南大学数学与统计学院

1 题目呈现

(2022全国甲卷文科数学第20题)已知函数f(x)=x3-x,g(x)=x2+a，曲线y=f(x)在点(x1,f(x1))处的切线也是曲线y=g(x)的切线.

(1)若x1=-1，求a；

(2)求a的取值范围.

2 解析

本题第(1)(2)问分析及解答过程如下.

对于第(1)问，已知函数f(x)与函数g(x)的公切线与f(x)切点的横坐标为x1=-1，可以从以下三个角度求参数a的值. 角度一，写出f(x)在x1=-1处的切线，可以选择联立切线方程与y=g(x)，借助Δ=0求a；也可以借助两函数在两切点处的导函数值相等，建立x1=-1与x2的关系式，再由切点(x2,y2)同在切线与函数g(x)上，建立a的方程求a.角度二，设出g(x)在点(x2,y2)处的切线，先探究x1=-1与x2的关系，再由切点(-1,0)在切线上，建立关于a的方程求a.角度三，分别用f(x)与g(x)的切点表示公切线，根据两切线斜率相等、截距相等构建关于x2与a的二元方程组，从而解出a的值.相应的思维导图如图1所示.

图1

角度一：写出f(x)在x1=-1处的切线.

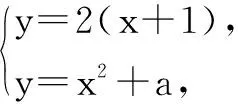
解法2-1：由f′(-1)=2，可知f(x)在x1=-1处切线l的方程为y=2(x+1).

因为切线l与曲线y=g(x)相切于点(x2,y2)，所以g′(x2)=f′(-1)，即2x2=2，得x2=1.

由于点(x2,y2)同在切线l与曲线y=g(x)上，故将点(x2,y2)代入l的方程，得y2=2(x2+1)=4.

因此g(x)与l相切于点(1,4)，代入y=g(x)，得4=12+a，解得a=3.

角度二：设出g(x)在切点(x2,y2)处的切线.

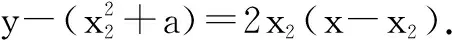
由切线l与曲线y=f(x)相切于点(-1,0)，得f′(-1)=g′(x2)，即2=2x2，则x2=1，从而l：y-(1+a)=2(x-1).再由点(-1,0)在切线l上，将点(-1,0)代入直线l，解得a=3.

角度三：分别用f(x)和g(x)的切点表示公切线.

解法4：f(x)在x1=-1处的切线l方程为

y=2(x+1). ①

点评：解法1中利用Δ=0来构建关于a的方程求a，仅适用于g(x)为二次函数，具有一定的特殊性.在处理公切线问题时，常常借助两函数在各自切点处的导函数值即为公切线的斜率，从而得到两切点横坐标的关系；再由切点同在切线与函数图象上，建立方程组进行求解.

对于第(2)问，在此问中，f(x)的切点由定点变为了动点，类比第(1)问的探究方法，可以从以下三个角度去求参数a的范围.角度一，用f(x)的切点表示公切线，将切线与y=g(x)联立，借助Δ=0得出a与x1的关系，进而去求a的范围；还可以先探究两切点横坐标之间的关系，由g(x)的切点同在切线与y=g(x)上，构建关于a与x1的等式，进而求a的范围.角度二，用g(x)的切点表示公切线方程，先探究两切点横坐标之间的关系，由f(x)的切点同在切线与y=f(x)上，构建关于a与x1的等式，进而求a的范围.角度三，用f(x)与g(x)各自的切点坐标表示公切线，借助公切线的两种表达形式的斜率、截距相等得出关于a与x1的等式，进而求a的范围.相应的思维导图如图2所示.

图2

角度一：用f(x)的切点表示切线.

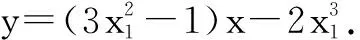
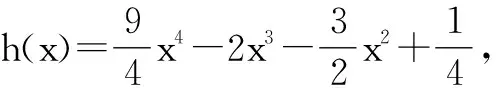
当x变化时，h′(x)，h(x)的变化情况如表1所示.

表1

所以a∈[-1,+∞).

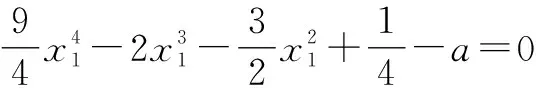
要使r(x)存在零点，即曲线y=γ(x)与x轴有交点，则r(x)min≤0，即-1-a≤0，所以a∈[-1,+∞).

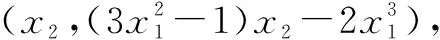
下同解法1-1或解法1-2.

角度二：用g(x)的切点表示公切线方程.

下同解法1-1或解法1-2.

角度三：用f(x)与g(x)的切点表示公切线.

解法4：曲线y=f(x)在点(x1,f(x1))处的切线l的方程为

设直线l与曲线y=g(x)相切于(x2,g(x2))，切线l的方程为

以下同解法1-1或解法1-2.

点评：从第(1)问中函数f(x)切点确定求参数a的值，到第(2)问中函数f(x)切点变化求参数a的范围，是从特殊到一般的过程，渗透了逻辑推理的核心素养，由参数求值问题过渡到参数求范围问题渗透了函数与方程的数学思想.本题第(1)问中处理两曲线公切线问题的思考角度在第(2)问中仍然适用.此外，在处理求参数范围的问题时，需先构建含有参数的等式，再转化为两曲线存在交点或函数存在零点的问题去求参数范围.

3 变型题

已知函数f(x)=x3-x,g(x)=x2+a，曲线y=f(x)在点(x1,f(x1))处的切线也是曲线y=g(x)的切线，则a的取值范围为.

秒杀法：图象法.

函数f(x)=x3-x的图象固定，函数g(x)=x2+a的图象随a的变化而沿着y轴方向变化，曲线y=g(x)与曲线y=f(x)的几类位置关系如图3～7.

图3

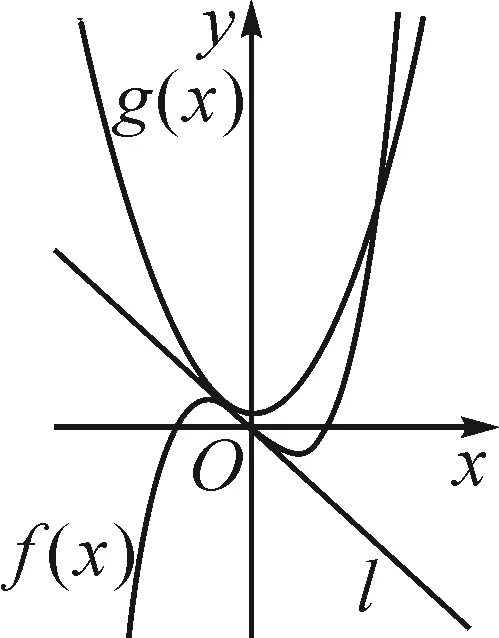
图4

图5

图6

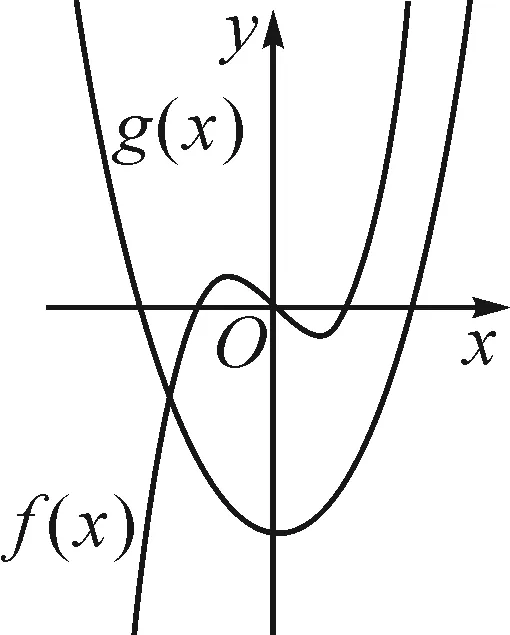
图7

直观观察两函数图象公切线的存在情况，可以发现，当f(x)与g(x)的相对位置属于前四种情况(图3～6)时，两函数图象均能找到公切线.当f(x)与g(x)的相对位置属于图7所表示的情况时，在两函数图象交点左侧，f(x)的导函数值恒为正值，而g(x)的导函数值恒为负值，不可能存在公切线；在两函数交点的右侧，由于g(x)图象恒在f(x)图象下方，所以也不可能存在公切线.综上，当f(x)与g(x)的位置关系属于图7所表示的情况时，两函数不存在公切线.

当函数f(x)与函数g(x)的图象在y轴右侧有共同切点的公切线时，设参数a的值为a0，当a≥a0时，f(x)与g(x)均存在公切线；当a

由点(1,y0)同在y=f(x)与y=g(x)上，得f(1)=g(1)，即0=1+a0，解得a0=-1.

由图象可知，当a≥a0=-1时，f(x)与g(x)存在公切线；当a<-1时，f(x)与g(x)不存在公切线.

综上，a∈[-1,+∞).

点评：在求解参数范围问题时，通常可以使用图象法寻找临界值进行求解，虽然在解答题中不够严谨而存在瑕疵，但在客观题求解中是常见方法.

链接1若直线y=kx+b是曲线y=lnx的切线，也是曲线y=ex-2的切线，则k=.

分析：分别设出直线与两曲线的切点坐标，求出导数值，得到两切线方程，再由两切线重合得斜率和截距相等，从而求得切线方程.

链接2(2018年天津卷理科第20题)已知函数f(x)=ax，g(x)=logax.

分析：两个函数的公切线问题可转化为二元方程组解的问题，通过消元，将方程组化为方程.而方程是否有解的问题可归结为连续函数的零点存在问题，即只要在区间上存在两个自变量，其函数值异号即可.

证明：曲线y=f(x)在点(x1,ax1)处的切线l1的方程为y-ax1=(x-x1)ax1lna.

有解.

1-x1lna=x2lna(lnx2-1).

再由⑤得x1lna+lnx2=-2ln(lna),故有

1+2ln(lna)+lnx2=x2lna(lnx2-1).

⑦

下证方程⑦有正实数解.

令r(x)=xlna(lnx-1)-lnx-2ln(lna)-1,则r(e)=-2ln(lna)-2≤0.那么由零点存在定理可知,只要找到一个x0>0,使r(x0)≥0即可.