“同构法”构造函数在解题应用中的一点商榷
姚顺禹 王恩普
⦿江苏省淮阴中学教育集团淮安市新淮高级中学
1 引言
在研究函数与导数中的一类恒成立问题时,如果能够在不等式的两边构造出相同的结构,借助于函数的单调性,剥去复杂的“外衣”,从而简化运算过程,通常把这种方法称为“同构”.对于同一个问题,由于角度不同,可能构造出的相同结构对应的函数略有差异,正是因为这一点,使得“同构法”引起了很多人的关注与研究.在学习同构法的过程中,有学生对其中的一种借助同构关系构造函数的解法产生了疑问.笔者查阅了多本期刊和网络资料,发现利用同构关系构造函数解决问题的时候,有些推理过程值得商榷,下面以2020年高考数学山东卷第20题的第(2)问为例,来做一些研究.
2 试题呈现
已知函数f(x)=aex-1-lnx+lna.
(1)当a=e时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;
(2)若f(x)≥1,求a的取值范围.
本文中只研究第(2)问借助同构关系构造函数的解法,首先来看下面的解析.
解析:由题意可知,函数f(x)的定义域为(0,+∞),且a>0.
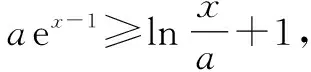
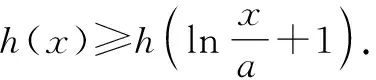
设g(x)=x-lnx+lna,则
当0
若x-lnx+lna-1≥0在(0,+∞)上恒成立,则只需g(x)min=g(1)=lna≥0,可得a≥1.
评注:上述过程采用了同构的思路,相比较直接求导研究最值的方法而言,避开了利用隐零点解决问题的过程,相对简单并且容易理解.
3 问题思考

前文已经提到,本题的恒成立问题有很多解决方案,此处仅对上文提及的同构法处理此类问题给出相应的改进方案.
改进方案一:分类讨论
解法1:由题意可知,函数f(x)的定义域为(0,+∞),且a>0.
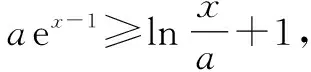
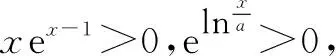
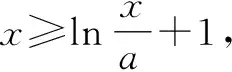
以下过程同原解答过程.
解法2:由题可知,函数f(x)定义域为(0,+∞),a>0.
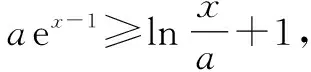
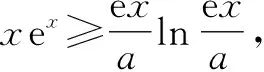
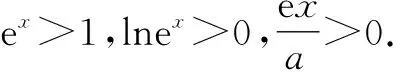
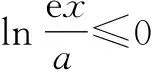

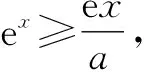
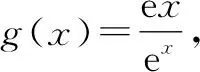
当0

评注:上述两种解答过程中利用同构“脱去外衣”的前提是在同一个单调区间内,如果不在同一个单调区间内,则要进行分类讨论.由于部分区间显然可以保证不等式恒成立,因此只需考虑在同一个单调区间内的情况,最后将两类情况综合即可.
改进方案二:改变同构形式
解析:由题意可知,函数f(x)的定义域为(0,+∞),且a>0.
由f(x)≥1,得aex-1-lnx+lna≥1,于是有ex+ln a-1≥lnx-lna+1,变形得
ex+ln a-1+x+lna-1≥lnx+x.
即ex+ln a-1+lnex+ln a-1≥x+lnx.
设g(x)=x+lnx,则有g(ex+ln a-1)≥g(x).
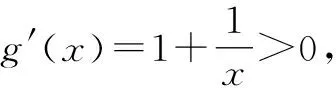
由g(x)的定义域为(0,+∞),得ex+ln a-1>0,且x>0.
所以ex+ln a-1≥x,即x+lna-1≥lnx在(0,+∞)恒成立.
以下过程同原解答.
评注:这样的同构形式与原解答的形式的区别在于,构造后g(ex+ln a-1)≥g(x)中的ex+ln a-1与x恰好都在所构造函数的同一个单调增区间内,可以顺利得出ex+ln a-1≥x,进而解决问题.
4 反思
《普通高中数学课程标准(2017版)》指出:逻辑推理是得到数学结论、构建数学体系的重要方式,是数学严谨性的基本保证,是人们在数学活动中进行交流的基本思维品质.在本文开头的解法中,如果只看结果与答案一致而忽视了过程的逻辑性,这对于数学学习是极其不利的.平时在解题过程中,必须要认真审视每一个步骤是否符合思维逻辑,培养用批判性思维考虑问题的习惯,勇于怀疑,敢于质疑,严密论证,科学推理,同时也能进一步促进创造性思维的形成.

