高精度轴类零件的砂带确定性修形方法*

胡 皓，陈学蕾，孙梓洲，戴一帆，关朝亮

(1. 国防科技大学 智能科学学院, 湖南 长沙 410073; 2. 超精密加工技术湖南省重点实验室, 湖南 长沙 410073;3. 国防科技大学 装备综合保障技术重点实验室, 湖南 长沙 410073)

金属轴类零件被广泛应用于各类旋转机械，涵盖了轻型和重型设备、常规精度到超高精度的各类零部件，其中精密机床的主轴就是高精度轴类零件的代表之一[1]。轴类零件的形状精度和尺寸精度是影响其工作性能的主要因素。圆(柱)度误差是衡量轴类零件形状的重要指标，关系到轴类零件的配合精度和回转精度[2]。随着超精密制造技术的发展，特别是航天、航空及国防等工业水平的提高，一些超精密轴类零件的圆度误差已达到0.1 μm的量级，圆柱度误差进入了1 μm的量级[3-5]。现有的超精密轴类零件的加工方法中主要有超精密外圆磨削为代表的传统加工方法，以及定心往复超精研、电化学机械光整、磁流体研磨、双平面方式超精研抛等非传统加工方法[6-9]。对于传统机械加工方法，轴类零件的最终精度一般由靠超精密的机床来保证，由于加工的“母性原则”，用一台超精密机床加工出来零件的精度不会高于机床自身的精度，目前超精密外圆磨削机床的加工精度只能达到0.2～0.3 μm的圆度误差，更高形状精度的轴类零件往往只能通过手工研磨获得。手工研磨为非确定性加工,精度收敛过程不精确，对操作者的要求很高,操作者需参照轴的测量数据进行研磨，研磨后再进行测量，并迭代多次，因此效率较低，人力成本高,难以实现经济的批量生产[10]。因此，急需除传统车削磨削加工工艺以外的可控柔体抛光新方法[11]，利用加工的“进化原则”，用精度相对较低的机床设备，加工出比机床自身精度更高的轴类零件。砂带抛光具有较高的生产效率，较好的加工表面质量，生产成本低，适用范围广等优势，已成为精密、超精密加工的可行方法之一[12]。将砂带研抛应用到轴类零件形状精度的确定性修形上，在制造过程中尽可能避免手工研磨,实现实用经济的超精密轴类零件的数字化、自动化加工，对进一步提高零件的加工精度以及精密、超精密测量和加工设备的研发具有重要意义。本文创新性地将光学确定性加工方法应用于轴类零件的加工，这种确定性加工方法有望突破机床自身的加工极限，利用非超精密机床加工高精度主轴。

1 轴类零件确定性加工原理

轴类零件的确定性加工原理基于计算机控制光学表面成形技术[13](computer controlled optical surfacing, CCOS)，即在去除函数和初始面形误差确定的条件下，通过准确的驻留时间算法解算出去除函数在工件表面各个位置的驻留时间，用数控系统控制不同位置的驻留时间以实现不同的去除量，从而实现圆柱零件形状误差的确定性收敛。

基于振动砂带辅助研抛的轴类确定性加工原理如图1所示，工件轴线和接触轮轴线平行，接触轮与轴类零件以恒压法向接触，外圈覆有硬度HA70橡胶的接触轮在接触压力下与工件之间能形成矩形的接触区域。接触轮被曲柄连杆驱动以一定的频率沿轴线方向振动来提供材料去除主运动，在振动的同时接触轮能沿着轴线方向进行伺服移动，通过和主轴旋转的联动伺服控制，接触轮能够遍历整个轴的表面。因为振动接触轮在单位时间内和恒定压强下去除工件表面材料的量是恒定的，因此在机床主轴的伺服控制下，工件不同位置在研抛区域中驻留不同的时间可以被去除不同量的材料，实现误差高点多去除，误差低点少去除，从而实现形状误差的确定性修整。相比传统车削磨削，该方法由于砂带在气缸的推动下始终以恒压与轴接触，即使接触轮沿轴线运动时有直线度误差、安装工件的主轴存在回转误差，以及传统加工中其他运动误差带来的影响，均可被气缸在恒压下的微位移所补偿。修形过程中砂带的磨损现象较为明显，为保证修形过程中的高材料去除效率和高去除稳定性，砂带需以一定的速度做更新运动，以保持研磨区域内磨粒有稳定的研抛状态。

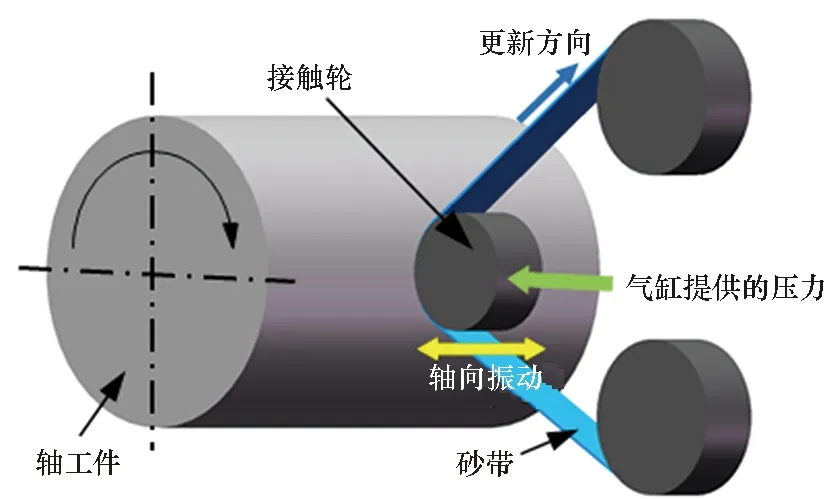
(a) 振动砂带辅助确定性修形三维示意图(a) 3D schematic diagram of vibrating belt assisted deterministic figuring

(b) 接触轮和工件之间接触示意图(b) Schematic diagram of the contact between contact wheel and workpiece图1 振动砂带辅助确定性修形示意图Fig.1 Schematic diagram of vibrating belt assisted deterministic figuring

2 轴类零件确定性加工仿真

形状误差为实际几何形状相对于理想几何形状的偏差，轴类零件的圆柱度误差为实测圆柱面要素对其理想圆柱面的变动量，当与圆柱度误差带形状一致的两同轴圆柱面紧贴包容实际圆柱面要素时，当其半径差为最小值时，这个最小值为圆柱度误差[14]。轴类零件形状误差的确定性修整是一种高点去除法，要确定性修整圆柱工件的形状误差，就需要将工件不同位置的相对位置关系进行测量与表达[15]。最小二乘圆柱法在求解理想圆柱面轴线的过程中，需要全部采样点的测量数据参与计算，进行重复测量以保证数据一致性，并且理想圆柱面轴线的位置能在多次测量中保持不变或者变动很小[16]，因此本文选用最小二乘圆柱法评定圆柱度误差。

图2(a)所示为经过1～15每转波动数高斯滤波的工件圆柱度误差分布，图2(b)为将圆柱工件沿着其中一条母线切开，将圆柱面展开为一个平面，圆柱表面误差对应表达则为平面的误差，将该平面作为初始误差表面进行确定性加工，当该误差平面收敛为绝对平面时，理论上会得到理想的圆柱面和圆轮廓。图2(c)为确定性轴类零件加工中的一个去除函数。去除函数可以理解为单位时间内，接触轮上的砂带在轴表面某一处位置产生材料去除量的分布矩阵。去除函数的获得方法为保持工件固定不动，利用覆有砂带的振动接触轮在工件表面某一位置定点磨削一段时间后，轴表面在该位置会产生一个去除斑点，通过圆柱度仪的检测和后期的提取得到。对去除函数以及初始误差分布利用脉冲迭代法[13]求取驻留时间进行仿真加工，得到的残差如图2(d)所示，仿真加工结果表明，仿真加工前后圆柱度误差从0.76 μm收敛到0.29 μm，验证了该确定性加工方法能实现柱面的确定性修形。

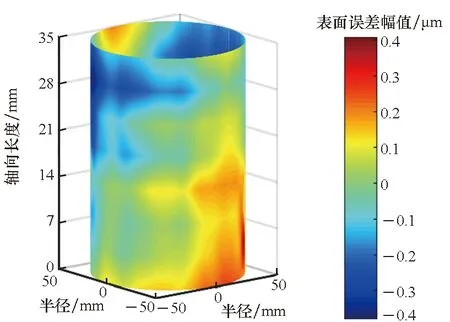
(a) 轴表面误差分布(a) Error distribution of shaft′s surface

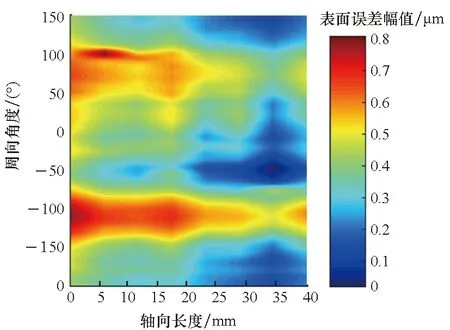
(b) 轴表面误差沿母线展开分布(b) Error distribution of expanded shaft′s surface cut by the generatrix

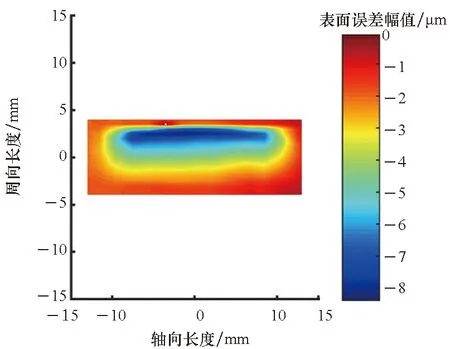
(c) 去除函数二维形貌(c) 2-D morphology of the removal function

(d) 仿真加工后残留误差(d) Residual error after simulated machining图2 仿真加工前的面形与加工后的残留误差Fig.2 Surface error distribution before and after simulated machining

3 确定性研抛实验平台介绍

3.1 砂带研抛实验平台介绍

依据图1所示的确定性修形原理示意图，轴类工件砂带确定性研抛方法的原理验证设备如图3(a)所示，该系统由一台经过改造的普通车床和一个振动砂带研抛机组成。机床的主轴被替换为具有伺服电机驱动的液体静压主轴，机床的Z轴安装了伺服电机和光栅线位移传感器，通过数控系统可以实现Z轴和C轴的伺服联动。砂带振动研抛装置安装在机床的Z轴溜板上，可随Z轴溜板共同移动；砂带研抛装置如图3(b)所示，由接触轮、砂带、振动模块、气缸、砂带轮、卷带轮等组成，外圈覆有橡胶的接触轮在气缸弹出时与零件接触并产生形变，形成一个矩形的研抛区域，通过精密调压阀的控制能保证在加工过程中接触轮与工件之间压强保持恒定，同时接触轮与工件之间的压力可调。接触轮在曲柄连杆的带动下可以沿着轴线方向进行振动以提供材料去除的主运动，砂带轮和卷带轮的旋转用来实现抛光区域内砂带的更新。机床Z、C两轴联动使得接触轮能到达轴表面的每一处位置。C轴在伺服电机的驱动下进行不匀速转动，可以控制轴表面不同位置在加工区域内的驻留时间长短，通过在轴表面指定位置的定量去除实现轴类工件的确定性修形。

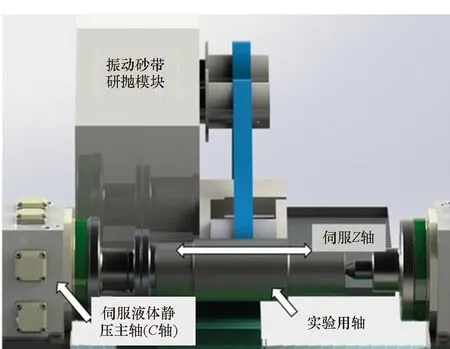
(a) 确定性砂带研抛机床(a) Abrasive belt-based polishing system

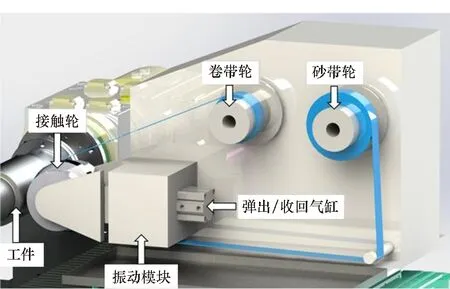
(b) 砂带研抛装置实物图(b) Abrasive belt polishing device图3 用于原理验证的砂带确定性研抛设备Fig.3 Abrasive belt deterministic figuring system used for principle verification

3.2 测量设备介绍

图4所示为Taylor Hobson Talyrond 565H主轴回转型圆柱度仪，其测量不确定度为30 nm，主轴测量角度分辨率为0.02°。安装在超精密气浮转台上的工件经过调平调心后[17]随转台回转，带有精密传感器的探针从底部到顶部检测若干个圆柱横截面上的圆轮廓，在一个圆截面上，圆柱度仪可以获得圆周上每个采样点的径向变动量，在后置算法中可获得单一圆截面上的轮廓和整个圆柱面的轮廓。

图4 圆柱度仪与工件Fig. 4 Cylindricity meter and the workpiece

4 轴类零件确定性修形抛光实验

4.1 确定性修形实验

为了验证外圆柱面确定性修形方法的可行性，利用上述砂带研抛装置对实验工件进行了确定性修形实验。实验工件为一根经过精密外圆磨削后的45#钢工件，其直径为100 mm，有效加工长度约为35 mm。利用如图4所示的圆柱度仪对修形实验前的工件从底部到顶部每隔5 mm测量一个圆轮廓，利用自带测量软件合成得到实验前的初始圆柱度误差分布，得到的初始圆柱度误差分布如图5所示，其圆柱度误差为0.76 μm。接触式测量中会不可避免地出现噪点，部分噪点会被测量软件自动滤除，被滤除的部分以白色的形式出现在彩色的表面测量轮廓中。

图5 加工前工件圆柱度误差测量结果(0.76 μm)Fig.5 Measurement results of workpiece′s cylindricity before machining(0.76 μm)

在加工前还需要在与被加工工件相同材料和半径的轴上制作并提取出去除函数。在制作去除函数以及后续的修形过程中，需要保证砂带的更新速度和接触压力恒定，恒定的加工参数能保证去除函数的长时稳定性，利于实现高精度修形。在砂带粒度不变的前提下，振动频率越高、接触压力越大、更新速度越快，去除函数的材料去除效率越高，接触轮在轴上每一处位置停留的时间也更短。在满足机床动态特性和砂带长度等因素的前提下，选用去除效率较高的加工参数组合。去除函数制作参数，即砂带粒度为5 μm，接触轮振动频率为7 Hz，接触压强为0.1 MPa，砂带更新速度为9 mm/s。图6所示为提取出的去除函数三维形貌。

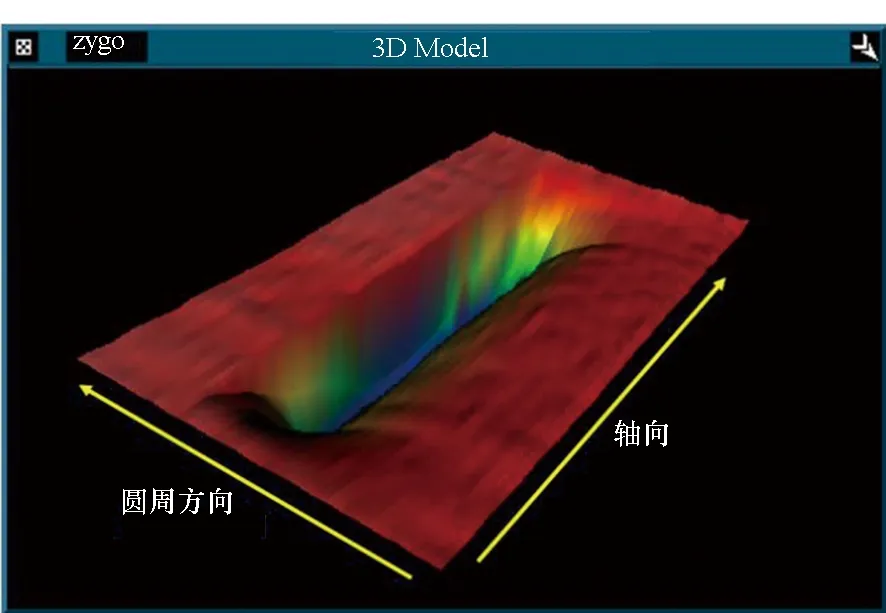
图6 提取出的去除函数Fig.6 Extracted removal function

利用此去除函数和之前已获得的工件表面误差分布，通过脉冲迭代法解算驻留时间，生成数控程序，进行了25 min左右的加工。加工过程中使用的工艺参数与制作去除函数的参数完全相同。

4.2 实验结果与分析

在经过加工后使用圆柱度仪对相同位置处的圆轮廓进行检测，测量得到了加工前后的圆柱度误差结果和圆截面上的圆度误差结果。加工后轴表面的形貌如图7所示，圆柱度误差从修形前的0.76 μm改善到0.35 μm，误差收敛比为2.17；加工前后所有截面上的圆度误差测量结果如图8所示，经过修形实验后，工件的平均圆度误差由0.42 μm收敛至0.11 μm，收敛比达到了3.82。选取其中一个截面上的测量轮廓进行对比，如图9所示，可以看到加工前圆轮廓上幅值较大的圆度误差已经得到有效收敛,但是轮廓上出现较多空间波长较短的误差分量。

图7 加工后工件圆柱度误差测量结果(0.35 μm)Fig.7 Measurement results of workpiece′s cylindricity after machining(0.35 μm)

图8 加工前后各截面上的圆度误差对比Fig.8 Comparison of roundness error of each section before and after machining

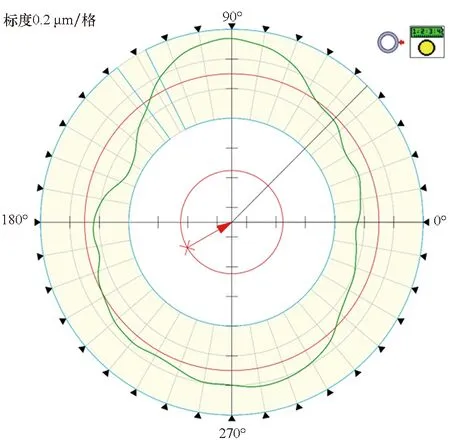
(a) 加工前的截面圆度误差(0.46 μm)(a) Roundness of one section before figuring (0.46 μm)

(b) 加工后的截面圆度误差(0.12 μm)(b) Roundness of one section after figuring (0.12 μm)图9 加工前后工件同一截面圆度误差测量结果Fig.9 Roundness of one section before and after figuring

5 结论

为了实现轴类零件圆柱度误差和圆度误差的确定性收敛，改善其形状精度，本文基于CCOS原理，创新性地将砂带研抛用于轴类零件的可控柔体抛光中。本文对柱面确定性修形的原理进行了介绍，并通过加工仿真验证了柱面确定性研抛可以使轴类零件的形状精度提高，在搭建的原理验证加工平台上进行了修形实验，得到的主要结论如下：

1)在柱面确定性研抛中，砂带轴向振动以提供材料去除主运动，通过机床主轴的伺服控制实现了工件不同位置在研抛区域不同的驻留时间，去除不同量的材料，从而实现圆柱度误差的确定性修整。

2)仿真结果验证了利用砂带确定性研抛外圆柱面的可行性，经过实际修形后，工件最终的圆柱度误差从0.76 μm改善到0.35 μm，所有圆轮廓的平均圆度误差从0.42 μm收敛到0.11 μm，加工精度已优于超精密外圆磨削。实验结果同时验证了确定性修形方法可使轴类零件形状精度进一步提升的可行性。但随着精度的进一步提升，圆度误差进入0.1 μm范围，逐渐趋近所使用圆柱度仪的测量精度极限，因此需要使用其他测量设备或方法来进行准确的柱面误差轮廓构建。

3)与其他确定性加工方法一样，随着迭代加工次数的增加，此种确定性修形方法也会在外圆柱面引入更多的中高频误差[18]和边缘效应[19]，并且从圆柱度误差和圆度误差数值以及轮廓形状的演变来看，在同一根轴上如果经过多次确定性修形，精度收敛会趋近极限，该精度极限与选择的工艺参数以及轮廓的误差分布有很大的关系，这些将留待后续进行研究。