电磁脉冲对高频结构的热效应分析*

袁玉章，孟 进，朱丹妮，王海涛，崔言程

(海军工程大学 舰船综合电力技术国防科技重点实验室， 湖北 武汉 430033)

高功率微波(high power microwave，HPM)技术[1-3]是从20世纪70年代逐步发展起来的一门新兴学科，是离子体物理、脉冲功率技术及电真空技术等相结合的产物。高功率技术发展至今，输出功率的进一步提高受到了材料特性和加工工艺等限制，各类型的高功率微波源均出现了射频击穿和脉冲缩短现象[4-9]。

对于Cerenkov型器件束波互作用区高频结构的射频击穿，有学者认为高频结构表面吸附气体的脱附电离是重要原因。此外，研究人员发现，金属材料表面距离相近的“微凸起”会对与其间隙垂直的射频磁场分量造成较为明显的场增强，在强射频磁场的作用下，该效应可能会使微凸起的温度急剧上升，导致其熔融蒸发。

针对高功率微波系统中由于微波的热损耗引起的气体脱附问题。本文就电磁脉冲对高频结构的热损耗进行理论分析、数值计算和仿真研究。本文可为高功率微波源的气体脱附以及射频击穿的研究提供参考与指导。

1 慢波结构的温升公式

(1)

其中，k是热导率，αd是热扩散系数。式(1)和初始条件、边界条件一起构成了完整的热传导方程。格林函数法在求解时将偏微分方程变为积分方程从而便于理论分析和数值计算，因此本文采用格林函数法[13-15]进行求解。

由于实际中的金属壁都不是理想导体，电磁波沿金属波导结构传播时会有功率损耗在波导壁上，电磁波将沿传输的方向逐渐衰减，电磁波在非理想导体中的衰减由切向磁场带来，进入波导壁的电磁波能量集中在波导壁的薄层中很快衰减并全部转化为焦耳热，从而加热金属壁。

考虑一维热传导模型，如图1所示，仅考虑温度在r方向的分布。此时由射频磁场带来的单位面积功率损耗为：

(2)

图1 一维模型示意图Fig.1 Diagram of one-dimensional model

单位体积的功率损耗为：

(3)

完整的热传导方程为：

(4)

采用格林函数法进行求解，对于r=0的平面，温升公式可化为：

(5)

(6)

2 数值计算与仿真研究

2.1 数值计算

金属材料的趋肤深度等参数与电磁脉冲频率紧密相关，对于频率f=9.38 GHz，脉宽100 ns的电磁脉冲，其在不锈钢、铜和铝中的趋肤深度等参数如表1所示。

表1 微波源常用材料的电参数(f=9.38 GHz，tp=100 ns)Tab.1 Electrical parameters of materials commonly used in microwave sources(f=9.38 GHz，tp=100 ns)

从表1可以看出，对于不锈钢材料，不满足在温升公式推导时的假设，不适用化简后的式(6)，须直接对式(5)进行数值积分求解其温升。

表2为常温下铜、不锈钢和铝的部分特性参数。

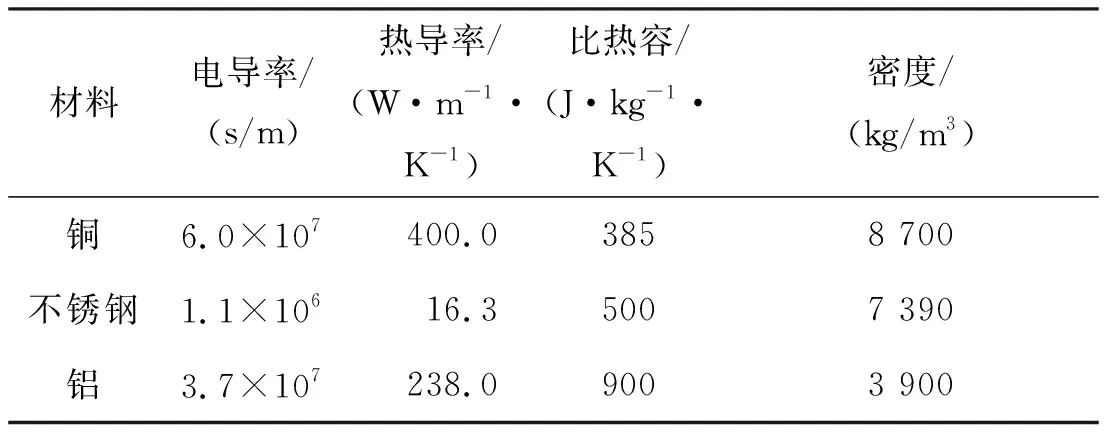
表2 常温下铜、不锈钢和铝的部分特性参数Tab.2 Partial characteristic parameters of copper, stainless steel and aluminum at normal temperature

下面对式(5)进行数值求解，定义积分项J，如式(7)所示。

(7)

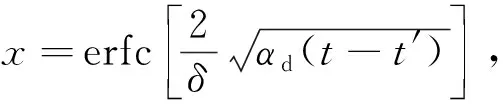
(8)

令F(x)=xex2erfc(x)，根据辛普森求积公式可知：

(9)

式(9)便是电磁脉冲对管壁加热温升的数值求解公式。

对于高功率微波源，束波互作用的模式多以TM01模式为主。式(10)是圆波导TM01模式的场表达式，可以看出其磁场只有角向分量，根据式Js=n×H可知，高频结构侧面的电流是径向的。

(10)

对于二周期1 MV·cm-1的试件(注入功率为2 GW)，图2为当传试件中传输 TM01模时，其中的磁场矢量分布，可以看出磁场分量平行于试件表面。图3是试件的表面磁场分布，从图中可以看出，试件最大峰值磁场位于表面，约为H‖=

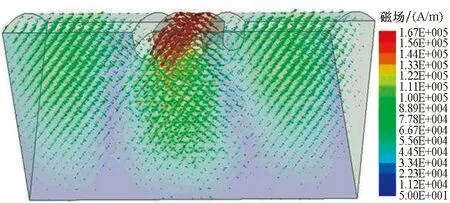
图2 TM01模式注入慢波试件时试件中磁场分布的矢量图Fig.2 Vector diagram of magnetic field distribution in slow wave structure when injected in TM01 mode

图3 二周期 1 MV·cm-1试件表面磁场分布Fig.3 Magnetic field distribution ion the surface of two periodic 1 MV·cm-1 slow wave structure

167 kA/m。此时用式(6)计算得到铜、不锈钢和铝试件的表面温升分别为3.4 ℃、113.6 ℃和5.4 ℃，利用式(9)得到的温升分别为2.8 ℃、21.7 ℃和4.4 ℃。结果表明，由于不锈钢材料的特性不满足推导过程的假设，采用式(6)计算温升得到的结果有很大误差。同时，上述分析计算结果表明单个百纳秒的电磁脉冲导致的高频结构加热温升不明显。

根据电磁脉冲的脉宽和试件表面的磁场分布，通过式(6)，便可计算得到高频结构的温升。在HFSS软件中导出高频结构表面的切向磁场仿真结果，计算功率2 GW、脉宽100 ns的电磁脉冲对不锈钢材料高频结构的加热温升。该1 MV·cm-1试件及相应区域的加热温升计算结果分别如图4和图5所示。

图4 二周期1 MV·cm-1矩形试件示意图Fig.4 Schematic diagram of two periodic 1 MV·cm-1 rectangular slow wave structure

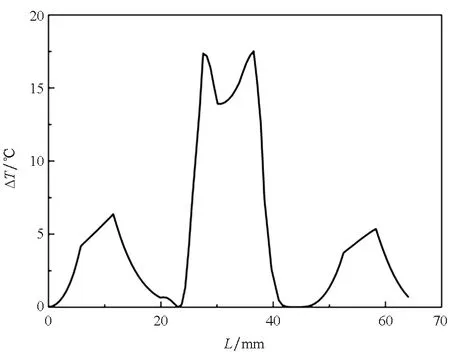
图5 二周期1 MV·cm-1不锈钢试件对应的表面温升Fig.5 Surface temperature rise of two periodic 1 MV·cm-1 stainless steel slow wave structure

从图5可以看出，单脉冲导致的温升不高，但当系统重频工作时，温升造成的释气可能会使高频结构倒角处的局部气压升高，而爆炸发射产生的电子轰击该处的气体层形成等离子体，造成射频击穿和脉冲缩短。接下来利用商业软件COMSOL对上述理论计算得到的结果进行验证。

2.2 仿真研究

利用商业软件COMSOL对微波的热损耗进行仿真研究，结果与数值计算进行对比[16]。

利用该软件的微波加热模块研究一定频率和功率的电磁脉冲注入高频结构时的加热温升效应。分析该问题须求解两个方程：与电磁场相关的麦克斯韦方程和与温度场相关的热传导方程。图6所示为求解模型的网格剖分，采用正四面体网格，真空区域的最大网格设置为导波波长的1/5。

图6 COMSOL模型的网格剖分Fig.6 Mesh division of the COMSOL model

通过波端口注入功率2 GW的纯TM01模，图7所示为试件中磁场的矢量分布，可以看出磁场在试件表面最大且只有角向分量，与理论计算和图2所示的仿真结果一致。

图7 试件中磁场的矢量图Fig.7 Vector diagram of the magnetic field in the slow wave structure

电磁脉冲的能量通过内表面耦合到试件中，将其内表面的损耗设置为热源。由于脉宽仅100 ns，因此将试件外壁设置为绝热边界，忽略与空气的散热过程。

图8所示为电磁脉冲结束时试件的温度分布，可以看出最高温度出现在磁场最大处，结果与理论计算一致。

图8 100 ns时不锈钢试件的温度分布Fig.8 Temperature distribution of stainless steel slow wave structure at 100 ns

对铜、不锈钢和铝在2 GW、9.38 GHz、100 ns 电磁脉冲注入情形下的温升进行了仿真研究。图9所示为仿真和理论计算结果的对比。可以看出对试件温升在电磁脉冲结束时达到最大值，且理论和软件仿真结果一致性较高。

图9 试件最高温度随时间的变化Fig.9 Variation of maximum temperature distribution of the slow wave structure with time

2.3 重频运行时的情况

当系统重频运行时，如图10所示，电磁脉冲循环加载于高频结构。假设电磁脉冲的脉宽为100 ns，由于脉宽较短，在脉冲持续时间内忽略散热效应，而在脉冲间隔中，需考虑散热效应，本文考虑的重频为1～30 Hz。

图10 重频运行下脉冲加热示意图Fig.10 Diagram of pulse heating in the case of repeated frequency

由于结构区域没有散热等外部冷却，仅考虑热传导，热传导方程如下：

(11)

(12)

边界条件为：

(13)

其中，rb为电磁脉冲温升的作用区域，T0是材料的初始温度，Tm为求解区域的最大温度。根据方程(11)～(13)可得：

(14)

对结果进行进一步化简可得：

=(Tm-T0)erf(x)+T0

(15)

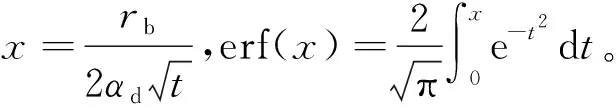
由式(15)可知，电磁脉冲间隔中的冷却与材料的热扩散率、冷却时间和温升作用的区域有关。

在电磁脉冲脉宽100 ns，试件表面最大射频磁场H‖=157 kA/m 时，对铜、不锈钢和铝材料试件在不同重复频率情况下的表面温升进行计算。研究中发现作用区域对金属材料温升的影响较为明显，根据实验结果合理选择参数，在重频10 Hz和30 Hz时铜、不锈钢和铝材料试件的最大温升计算结果如图11所示。在电磁脉冲持续时间里，温度上升，前一个脉冲结束后，试件表面温度缓慢下降直到下一个脉冲到来。由于材料特性等原因，单脉冲对铜和铝试件的温升作用低，且在脉冲间隔时温度降低较为明显，几乎没有温度升高的趋势。而对于不锈钢材料，当重复频率较高时，表面温升有可能达到气体热脱附的阈值[17]。

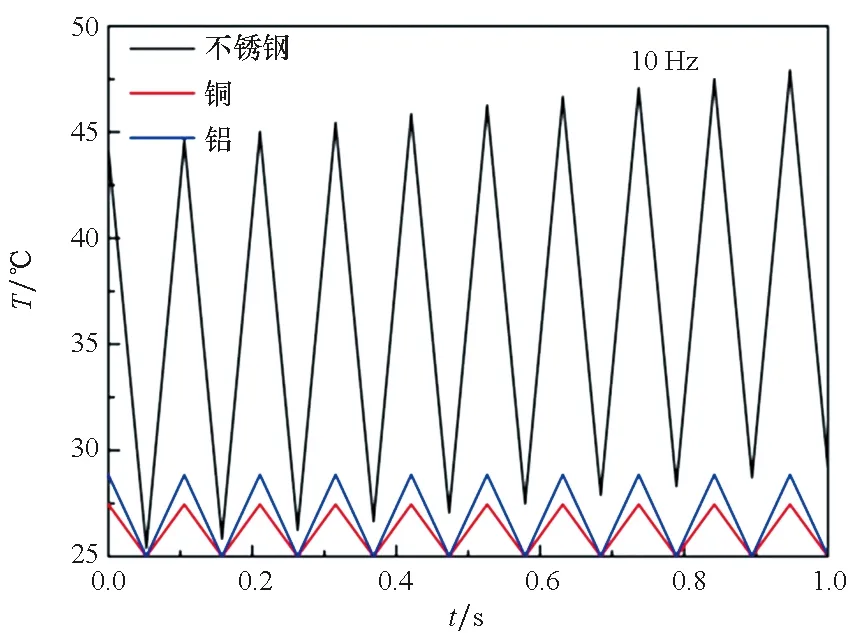
(a) 10 Hz

(b) 30 Hz图11 典型重复频率时三种金属材料的表面温升Fig.11 Surface temperature rise of three metal material at typical repeated frequency

高功率微波源中的热效应包含本文研究的微波热损耗导致的温升及电子束轰击收集极产生的温升效应等，是一个综合的结果，热效应对于射频击穿的影响需要进一步研究分析。

3 结论

本文对 HPM 源中高频结构的热损耗通过理论分析、数值计算和仿真分析等方法进行了研究，得到了如下结论：

电磁脉冲对金属材料的加热温升式(6)有适用范围，对于不锈钢等材料，须用数值方法进行求解；以二周期 1 MV·cm-1试件为例进行的求解结果表明：脉宽100 ns 的单脉冲对不锈钢试件的温升效应明显高于其他材料；当系统工作在高重频时，电磁脉冲的温升作用有可能使金属材料达到气体脱附的阈值从而引发气体脱附形成局部高压；COMSOL软件的仿真研究结果和理论计算结果符合良好。