多核数字信号处理器矩阵乘卷积算法性能评测*
王庆林,裴向东,廖林玉,王浩旭,李荣春,梅松竹,李东升
(1. 国防科技大学 计算机学院, 湖南 长沙 410073;2. 国防科技大学 并行与分布处理国防科技重点实验室, 湖南 长沙 410073)
随着人工智能+(artificial intelligence+, AI+)的快速发展,深度学习技术逐渐在各个领域实现了技术落地。作为一类代表性深度神经网络,卷积神经网络(convolutional neural networks, CNNs)被广泛应用在各种场景中,如自动驾驶[1]、视频处理[2]、科学计算[3]等。在CNNs中,卷积层占据了大部分的计算开销,从而使得卷积层的优化成为CNNs网络性能的关键,目前成为学术界和工业界研究的热点。
实现卷积层计算的方法主要有直接卷积[4-5]、快速傅里叶变换(fast Fourier transform, FFT)卷积[6-9]、Winograd卷积[10-11]、矩阵乘卷积[12-14]四种算法。直接卷积算法根据卷积层的定义直接进行实现,为获得较高的性能,通常需要针对卷积核大小、卷积步长等卷积参数进行优化。FFT和Winograd卷积算法分别通过FFT和Winograd转换来降低卷积复杂度,因此这两种算法也常被称为快速卷积算法。尽管如此,快速卷积算法通常只适用于部分卷积配置,如Winograd算法通常只适合于卷积核大小为3×3的情况。矩阵乘卷积算法是将卷积计算转换为通用矩阵乘操作,是实现卷积计算的通用算法,是PyTorch[15]、TensorFlow[16]等深度学习框架以及cuDNN[17]、oneDNN[18]等神经网络库首要提供的算法。矩阵乘卷积算法可分为显式算法和隐式算法。如果矩阵转换和矩阵乘融合为一体,则无须存储完整的转换矩阵,称为隐式算法,否则称为显式算法。本文主要聚焦显式矩阵乘卷积算法,构建完整的转换矩阵,通过调用已有的矩阵乘函数库来实现卷积计算,为各种卷积参数配置提供高性能实现基础。
FT-M7032是国防科技大学面向E级计算自主研发的一款异构通用多核数字信号处理器[19](digital signal processors, DSP),由32个通用DSP核和1个16核ARMv8 CPU构成。在主频为1.8 GHz时,全芯片的单精度浮点峰值性能高达11.06 Tflops/s,在科学计算和人工智能等领域具有巨大的潜力。在FT-M7032中,计算能力主要由32个通用DSP核提供。为了降低芯片面积和功耗,通用DSP核采用基于超长指令字的顺序执行架构,并采用软件控制的存储作为片上缓存,然后基于直接存储器存取(direct memory access,DMA)部件进行不同存储层次之间数据的传输。然而,面向CPU、GPU等芯片的已有算法在FT-M7032上没法直接运行或者没法实现高的性能。因此,针对多核DSP的体系结构进行算法优化是FT-M7032发挥高性能计算的必要措施。
面向FT-M7032处理深度学习应用的需求,本文结合其体系结构特征,在详细分析了FT-M7032芯片上实现显式矩阵乘卷积算法的各种技术路径的基础上,提出了一种面向多核DSP架构的高性能并行显式矩阵乘卷积实现算法ftmEConv,并采用了不同的卷积配置对算法进行了详细性能评估。测试结果显示,ftmEConv性能均超过了FT-M7032芯片上的其他显式矩阵乘卷积实现方法,获得了高达7.79倍的加速,最高达到了42.90%的多核DSP峰值性能。同时,针对算法开销进行了详细分析,也为后续面向FT-M7032的算法优化指明了方向。本文工作对于推动FT-M7032在人工智能领域的应用,以及面向FT-M7032的算法与应用优化,均具有重要的意义。
1 相关定义
1.1 卷积定义
本文的研究范围仅限于二维经典卷积,故令卷积的输入特征图为I[N][Cd][Hi][Wi][L],输入卷积核为F[C][Kd][Hf][Wf][L],卷积的输出特征图为O[N][Kd][Ho][Wo][L]。其中,N表示输入特征图的数量,Hi/f/o和Wi/f/o分别表示空间上的高度和宽度,L表示硬件向量处理单元并行处理的数据宽度,Cd和Kd分别表示输入通道和输出通道的分块数,输入通道数为C=Cd×L,输出通道数K=Kd×L。卷积计算中的步长大小标记为S,填充大小标记为P,则输出特征图的高度和宽度分别为:Ho=(Hi+2×P-Hf)/S+1,Wo=(Wi+2×P-Wf)/S+1。基于以上参数表示,深度学习领域中的卷积定义如下:

Fcd×L+cl,kd,hf,wf,kl)
(1)
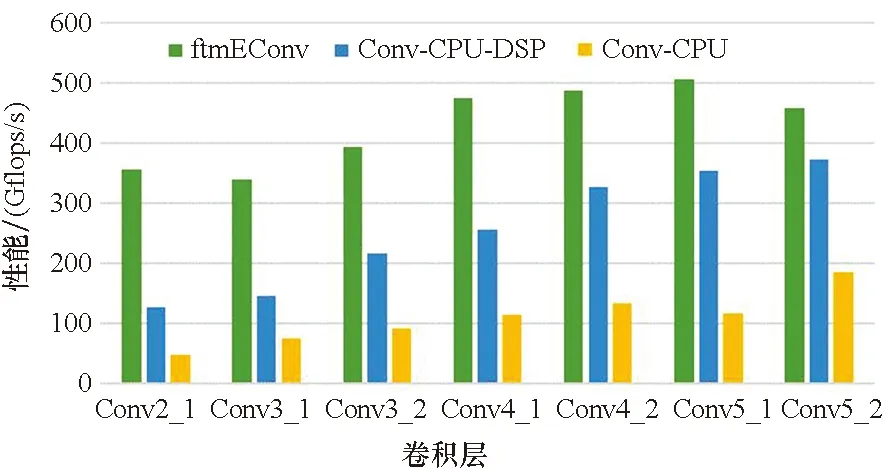
其中,0≤n 矩阵乘卷积算法是将卷积操作直接转换为通用矩阵乘计算。根据第1.1节卷积的定义,矩阵乘卷积的算法大致分为四步,如算法1所示。第一步(Step 1)是输入特征图转换,根据卷积操作的计算过程将输入特征图I转换为A矩阵。该步骤将单个通道特征图上的一个卷积点计算以及多输入通道上的累加操作所需来自I的全部元素转换为A矩阵的一行,称为im2row (image-to-row)操作;如果转换为A矩阵的一列,则称为im2col (image-to-column) 操作。本文后续讨论中主要涉及im2row操作,A矩阵常采用A[M′][K′]表示,其中M′=N×Ho×Wo,K′=Cd×Hf×Wf×L,同时也根据算法的设计讨论需求采用其准确的数据布局A[N][Ho][Wo][Cd][Hf][Wf][L]表示。第二步(Step 2)将卷积核F转换为B[K′][N′]矩阵,其中N′=K。第三步(Step 3)执行矩阵乘操作C=A×B,其中C矩阵大小为M′×N′。第四步(Step 4)将C矩阵转换为卷积的输出特征图O。 算法1 原始矩阵乘卷积算法Alg.1 Original matrix multiplication-based convolutional algorithm FT-M7032是国防科技大学面向E级计算自主研发的一款异构通用多核DSP,由一个16核ARMv8 CPU和4个GPDSP簇构成,其整体架构如图1所示。ARMv8 CPU上运行Linux操作系统,负责进程与外设管理以及多芯片之间的通信,单精度浮点峰值性能为281.6 Gflops/s。4个GPDSP簇提供主要的计算能力支持,其中每个GPDSP簇由8个通用DSP核和大小为6 MB的全局共享内存(global shared memory, GSM)通过交叉开关网络连接而成。片上GSM带宽约为307.2 GB/s。当DSP内核主频为1.8 GHz时,单个GPDSP簇可以提供高达2.76 Tflops/s的单精度浮点计算能力。CPU与4个GPDSP簇共享全局内存空间,但每个GPDSP簇只能访问对应的局部DDR内存空间。单个GPDSP簇对应的内存空间理论带宽为42.62 GB/s。 图1 FT-M7032芯片的整体架构Fig.1 Architecture of FT-M7032 FT-M7032中单个DSP核的微架构如图2所示,主要由标量处理单元(scalar processing unit, SPU)、向量处理单元(vector processing unit, VPU)、指令调度单元(instruction fetch unit, IFU)以及DMA部件等构成。SPU负责标量计算与流程控制,主要包括标量处理部件(scalar processing elements, SPE)和64 KB标量存储(scalar memory, SM)。SM与寄存器之间的访问带宽为28.8 GB/s。VPU负责向量计算,主要由16个向量处理部件(vector processing elements,VPE)与768 KB向量存储(vector memory, AM)构成。每个VPE包含3个浮点乘累加(floating point multiply accumulator, FMAC)部件、1个位操作(bit processing, BP)单元以及2个Store/Load部件,支持6条对应指令并行执行。16个VPE以单指令多数据(single instruction multiple data, SIMD)的方式协作运行,一次可以处理32个单精度浮点数据(FP32),即对于FP32数据,L=32。AM每个周期可以向向量寄存器提供 512 B数据,即AM与向量寄存器之间的带宽为921.6 GB/s。 图2 FT-M7032中DSP单核微架构Fig.2 Micro-architecture of each DSP core in FT-M7032 对照矩阵乘卷积算法的详细步骤以及FT-M7032的体系结构可知,在FT-M7032上实现高性能矩阵乘卷积算法主要有三种方法。 第一种方法是将矩阵乘卷积算法的四个步骤全部运行在FT-M7032的16 核ARMv8 CPU上,其中第三步的矩阵乘通过调用ARMv8 CPU上的BLAS库来完成。该方法的优点是能够在FT-M7032上快速实现矩阵乘卷积算法,且工作量较小。但是该方法没有充分利用FT-M7032中GPDSP簇强大的计算能力,毕竟GPDSP簇的性能远高于16核ARMv8 CPU的性能。为便于后续的讨论与分析,统一将该方法标记为Conv-CPU。 第二种方法是将Conv-CPU中的矩阵乘迁移到其中一个GPDSP簇上执行,即第三步的矩阵乘通过调用GPDSP簇上的BLAS库来完成。为了保证CPU对四个簇的平衡控制,该方法实现其他三个步骤时,均只运行在单个GPDSP簇对应的四个CPU核上,即执行第一、二与四步骤时,并行的线程数均为4。为便于后续的讨论与分析,统一将该方法标记为Conv-CPU-DSP。 第三种方法是将矩阵乘卷积算法的四个步骤全部运行在FT-M7032的GPDSP簇上。与前面两种方法相比,该方法既能充分利用GPDSP簇的计算能力,也能基于DSP中的DMA部件提升DDR的访存效率。难点在于如何面向多核DSP的体系结构高效实现im2row、transformF以及transformO等访存密集型操作。 本文面向FT-M7032的矩阵乘卷积算法实现将采用第三种方法,拟基于AM与GSM相对DDR的高带宽属性,通过调用DMA操作、向量Load/Store操作的方法来高效实现im2row、transformF以及transformO等访存密集型操作,并通过集成已有的矩阵乘算法来高效完成矩阵乘操作。为便于后续的讨论与分析,将本文基于第三种方法的实现统一标记为ftmEConv。 基于第3节的分析,并结合FT-M7032的体系结构特征,本文提出了面向多核DSP的矩阵乘卷积算法ftmEConv,由六个步骤构成,如算法2所示。第一步(Step 1)将CPU 缓存中的内容写回DDR中。第二步(Step 2)调用DSP端函数__im2row( )完成输入特征图的转换。第三步(Step 3)调用DSP端函数__transformF( )完成卷积核的转换。第四步(Step 4)调用DSP端函数__gemm( )完成矩阵乘的计算。第五步(Step 5)调用DSP端函数__transformO( )完成输出特征图的转换。第六步(Step 6)作废CPU Cache中的内容,完成卷积运算。 算法2 面向多核DSP的并行矩阵乘卷积算法ftmEConvAlg.2 Parallel matrix multiplication-based convolutional algorithm on multi-core DSP (ftmEConv) 总的来说,ftmEConv的主要操作过程(输入特征图转换、卷积核转换、矩阵乘以及输出特征图转换)均运行于通用DSP核上,通过有效挖掘通用DSP核的潜力来提升矩阵乘卷积的性能。同时,ftmEConv的设计也使得数据在CPU端与DSP端之间的转换开销大幅降低,过程中仅需进行一次DSP读转换(Step 1)和CPU读转换(Step 6)操作即可。 结合GPDSP簇的体系结构特征,本文提出了面向多核DSP的im2row算法的并行实现方法, 如算法3所示。该实现方法充分利用了片上AM和GSM相对DDR的高带宽特性,将输入特征图进行分块后传入AM空间,然后基于DMA函数先后完成两个维度的转换操作。具体为:在分块参数计算方面,鉴于深度学习中主流CNNs所处理的输入特征图空间维度相对较小等因素,同时根据片上AM和GSM空间大小的估计,本文决定将I传入片上空间最小粒度设置为Wi×L,即不在Wo维度上进行分块。根据Wi、Hi、S以及P等参数计算将I传入AM空间扩展后的特征图空间大小W′i=(Wi+2×P+S-1)/S×S、H′i=(Hi+2×P+S-1)/S×S(第1行),从而使得填零后的特征图每行首个元素与每个通道首个元素均可以成为按步长S横向滑动后的卷积窗口中的首个元素。在算法3设计中,由于扩展后的分块输入特征图I′am和转换后的矩阵A′am/gsm分别存储在不同片上空间中,因此计算分块参数时,以I′am和A′am/gsm中的存储空间需求最大值来进行约束。同时,按以下原则来进行分块大小的调整:先设置N、Cd、Ho维度上的分块大小Nb、Cdb、Hob分别为1;在片上空间限制下,尽可能先增大Hob;如果Hob=Ho,再尽可能增大Cdb;如果Cdb=Cd,然后尽可能增大Nb。 算法3 im2row操作的并行实现Alg.3 Parallel implementation of im2row algorithm 通过算法3中第3~9行的for循环,将输入特征图I划分成形状为[nb][cdb][hib][Wi][L]的众多子块I′ddr,然后采用多个DSP核分别调用im2row_kernel()函数来并行处理不同的子块。 im2row_kernel()函数是本方案中实现im2row功能的核心函数,一共由五步构成,如算法3中第11~16行所示。下面以nb=1、cdb=1、Hib=Hi=3、Wi=3、Hf=Wf=2、S=2以及P=1为例进行每一步的详细介绍,如图3所示,其中每一个元素表示一个长为L的向量。 图3 im2row_kernel()的实现实例Fig.3 An implementation example for im2row_kernel() 第一步(第12行的Step 1):根据P的情况进行AM空间的初始化。如果P不等于0,则意味着卷积计算过程中需要对特征图空间进行补零操作,本文通过对AM空间提前进行快速置零初始化来实现补零操作;如果P等于0,则跳过此步的初始化。如图3中所示,由于P等于1,则需将AM空间初始化为零。 第二步(第13行的Step 2):调用nb×cdb次DMA函数将输入特征图的子块Iddr[nb][cdb][hib][Wi][L]传入AM空间,并完成补零与扩展操作,从而将传入的输入特征图子块扩展为AM中的I′am[nb][cdb][h′ib][W′i][L],其中h′ib表示传入的hib经过补零与扩展后的大小。在图3中,W′i=6、h′ib=6;“0”表示补零后产生的向量,这是卷积计算的需求;“x”表示扩展后行和列中的无效向量元素,扩展后的子块在Step 3中即可通过一次DMA函数调用完成Wf维度的铺平转换。 第三步(第14行的Step 3):调用一次DMA函数将AM空间中的I′am[nb][cdb][h′ib][W′i][L]传输到GSM中,转换成Agsm[nb][cdb][h′ib][Wo][Wf][L]。在本步实现中,将I′am[nb][cdb][h′ib] [W′i][L] 当作I′am[nb×cdb×h′ib×W′i][L]来处理,通过合理设置DMA函数调用中的源块数、源块大小、源偏移量、目的块数、目的块大小以及目的偏移量来实现Wf维度的转换,其中通过将目的偏移量设置为负值来把矩阵中间扩展的“x”去掉。 第四步(第15行的Step 4):调用nb×cdb×Hf次DMA函数将GSM空间Agsm[nb][cdb][h′ib][Wo][Wf][L]传输到AM空间中,变成Aam[nb][hob][Wo][cdb][Hf][Wf][L],其中既涉及Hf维度的铺平转换,也涉及多个维度(如hob×Wo维度与cdb维度)之间的转置。 第五步(第16行的Step 5):调用一次DMA函数将Aam[nb][hob][Wo][cdb][Hf][Wf][L]传输回DDR空间A[N][Ho][Wo][Cd][Hf][Wf][L]中对应位置。 对于1×1卷积来说,F与B完全相同,因而不需要进行任何转换;对于其他如3×3等的卷积来说,需要对F进行格式转换,本文的实现如算法4所示。在分块方面,由于Hi和Wi通常较小,在实现中仅需根据AM空间大小在C和Kd两个维度进行分块。单个GPDSP簇中8个通用DSP核并行将F分块后的子块传入AM空间(第6行),完成格式转换(第7行),然后传出到DDR中B的给定位置(第8行)。 算法4 卷积核张量的并行转换Alg.4 Parallel transformation of filter tensors 由于面向FT-M7032芯片的软件生态尚不完善,特别是如BLAS等数学库均没有成熟的版本,本文先根据文献[20]构建了基于N′维度并行的矩阵乘实现函数TGEMM。然后,在TGEMM与不规则形状矩阵乘函数库ftIMM[19]之间根据N′的大小进行选择,如算法2中第7~11行所示。在TGEMM实现中,每个DSP核一次处理N′维度上的分块大小为96,只有N′≥8×96=768时,才能保证单个GPDSP簇中8个DSP核都能分配到相应的计算任务。为充分发挥单簇中所有DSP核的并行计算能力,只有当N′≥768时,才调用TGEMM函数;否则,调用ftIMM中的优化实现。 在完成第4.4节矩阵乘函数调用后获得矩阵C[M′][N′],还需将其转换成卷积的输出特征图格式。本文提出了如算法5所示的输出特征图张量并行转换算法。在分块方面,由于主流CNNs中的K相对较小,因而根据片上AM空间大小,仅在N和Ho×Wo两个维度上进行分块。单个GPDSP簇中8个通用DSP核并行将分块后多个C子块传入AM空间(第6行),完成格式转换(第7行),最后传出到DDR中O的给定位置(第8行)。 算法5 输出特征图张量的并行转换Alg.5 Parallel transformation of output feature maps tensors 本节主要涉及ftmEConv与第3节所介绍的Conv-CPU、Conv-CPU-DSP之间的性能对比。其中,Conv-CPU所有部分均运行在FT-M7032的16核ARMv8 CPU上,矩阵乘部分直接调用OpenBLAS v0.3.1[21]中的cblas_sgemm函数实现;Conv-CPU-DSP中转换部分运行在FT-M7032中一个GPDSP簇对应的4个ARMv8 CPU核上,矩阵乘部分则直接采用ftmEConv中矩阵乘的实现(第4.4节)。同时,三种算法实现均在相同的带宽下运行,即所有内存空间均分配在一个GPDSP簇匹配的局部内存空间。 在本节中涉及三个指标来表示卷积的性能,第一个是完成卷积计算的时间T,第二个是卷积计算所到达的计算性能Pconv,第三个是卷积计算在单个GPDSP簇上所实现的计算效率Econv。三个指标之间的相互关系如式(2)与式(3)所示,其中Peakgpdsp表示单个GPDSP簇的峰值性能。 (2) (3) 本小节首先对运行在FT-M7032中一个GPDSP簇上ftmEConv实现的时间开销进行深度剖析,然后对ftmEConv、Conv-CPU以及Conv-CPU-DSP三种实现中占比相对较大的输入特征图转换进行性能对比分析。 当N=32、Hf=Wf=3、Hi=Wi=28、S=1以及P=0时,ftmEConv中各部分开销的占比随C=K取不同值的变化情况如图4所示。ftmEConv的开销主要由输入特征图转换(输入转换)、卷积核转换、矩阵乘以及输出特征图转换(输出转换)四部分组成。当C=K取不同值时,最耗时的始终是矩阵乘GEMM与输入转换im2row两部分。随着C=K增大,矩阵乘部分的占比逐渐增大,最大达到了92.41%,因而矩阵乘的性能是决定矩阵乘卷积性能的关键因素。尽管如此,输入转换im2row部分也始终占据一定比例的开销。在图4所示的测试中,输入转换im2row部分开销占比在5.77%~33.83%之间。 图4 ftmEConv在不同通道数设置下的开销分析Fig.4 Overhead analysis of ftmEconv with different channel sizes 当N=32、Hf=Wf=3、Hi=Wi=28、S=1以及P=0时,ftmEConv、Conv-CPU-DSP以及Conv-CPU三种实现中输入转换im2row部分的性能随C=K取不同值的变化情况如图5所示。 图5 三种实现在不同通道数设置下的输入特征图转换性能Fig.5 Input transform performance of three implementations with different channel sizes 本文采用有效带宽来衡量输入转换部分的性能,即采用输入转换部分的理论数据访问量(等于I和A两个张量大小之和)除以其耗时。ftmEConv中的输入转换部分实现了24.9~29.97 GB/s的性能,对应的DDR带宽利用效率为58.42%~70.32%。同时,ftmEConv中输入转换部分显著优于Conv-CPU-DSP与Conv-CPU两者的实现,分别实现了高达3.23倍与3.75倍的性能加速。 本小节将采用不同的卷积参数配置对ftmEConv、Conv-CPU-DSP以及Conv-CPU三种实现进行全面的性能评测。 当C=K=384、Hf=Wf=3、Hi=Wi=28、S=1以及P=0时,三种实现性能随N不同取值的变化情况如图6所示。ftmEConv的性能Pconv达到了555.08~686.78 Gflops/s,对应的计算效率Econv为20.08%~24.84%。相比Conv-CPU-DSP,ftmEConv实现了1.43~1.61倍的性能加速,主要来源于面向多核DSP的三个转换过程的性能优化。相比Conv-CPU,ftmEConv实现了4.73~5.13倍的性能加速,除了三个转换过程的优化外,也得益于占比最大的矩阵乘部分的性能提升。 图6 三种实现在不同输入特征图数量设置下的性能Fig.6 Performance of three implementations with different numbers of input feature maps 当N=32、Hf=Wf=3、Hi=Wi=28、S=1以及P=0时,三种实现性能随C=K取不同值的变化情况如图7所示。ftmEConv的性能Pconv随着C=K增大而逐渐增大,最终达到了1 186.10 Gflops/s,计算效率Econv也达到了42.90%。相比Conv-CPU-DSP与Conv-CPU,ftmEConv分别实现了1.24~2.10 倍与4.87~7.79倍的性能加速。 图7 三种实现在不同通道数设置下的性能Fig.7 Performance of three implementations with different channel sizes 当N=32、C=K=384、Hf=Wf=3、S=1以及P=0时,三种实现性能随Hi=Wi取不同值的变化情况如图8所示。ftmEConv的性能Pconv随着Hi=Wi减小而逐渐降低,当Hi=Wi=7时,Pconv为263.60 Gflops/s。主要原因是随着Hi=Wi减小,矩阵乘的维度M′快速变小,使得矩阵乘的性能逐渐降低,从而影响了ftmEConv整体的性能。尽管如此,ftmEConv仍然在所有测试卷积层上获得了优于Conv-CPU-DSP与Conv-CPU两种实现的性能,相应的性能加速比分别为1.19~1.58与2.41~5.07。 图8 三种实现在不同输入特征图大小设置下的性能Fig.8 Performance of three implementations with different input feature maps sizes 当N=32、C=K=384、Hi=Wi=28、S=1以及P=0时,三种实现性能随Hf=Wf取不同值的变化情况如图9所示。ftmEConv的性能Pconv在Hf=Wf=1时最低,在Hf=Wf=9时最高,相应的计算效率Econv分别为16.96%与29.35%。相比Conv-CPU-DSP,ftmEConv在Hf=Wf=1时获得了最大3.87倍的性能加速,主要是输入转换与输出转换部分的开销占比较大造成的。与Conv-CPU相比,ftmEConv获得了4.41~6.23倍的性能加速。 图9 三种实现在不同卷积核大小设置下的性能Fig.9 Performance of three implementations with different kernel sizes 在本小节,采用典型网络Resnet18[22]中的卷积层来进行三种实现之间的性能对比测试,结果如图10所示。在图10中,横坐标表示来自Resnet18中的不同配置卷积层,其中N均设置为128。与第5.3节的性能对比分析结果相似,在所有测试的卷积层上,ftmEConv均优于Conv-CPU-DSP与Conv-CPU两种实现。具体而言,ftmEConv获得了348.42~512.87 Gflops/s的性能,计算效率为12.60%~18.55%;相比Conv-CPU-DSP与Conv-CPU,分别实现了1.22~2.85倍与2.80~7.09倍的性能加速。 图10 三种实现在Resnet18网络层上的性能Fig.10 Performance of three implementations for convolutional layers of Resnet18 本文针对飞腾异构多核DSP的体系结构特征与矩阵乘转置操作的特点,提出了一种面向多核DSP架构的高性能并行显式矩阵乘卷积实现算法ftmEConv。ftmEConv由输入特征图转换、卷积核转换、矩阵乘以及输出特征图转换四个并行化部分构成,四个部分均运行在通用多核DSP上。ftmEConv通过有效挖掘多核DSP的潜力来提升各个部分的性能,同时大幅降低了CPU端与DSP端之间的转换开销。实验结果显示,ftmEconv能够显著加快FT-M7032芯片上的矩阵乘卷积操作,其计算效率最高达到了42.90%;与FT-M7032芯片上的其他实现相比,获得了1.18~7.79倍的性能加速。该项研究对于推动国产DSP在人工智能领域的广泛应用具有重要意义。 下一步将研究面向多核DSP的其他卷积算法实现,以期进一步提升FT-M7032芯片上的卷积实现性能。1.2 矩阵乘卷积算法

2 FT-M7032体系结构
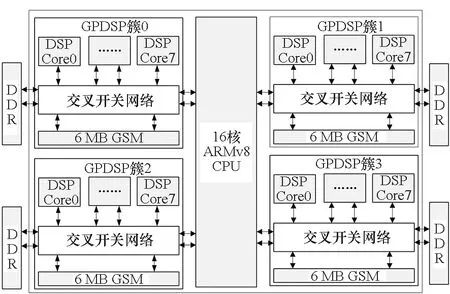
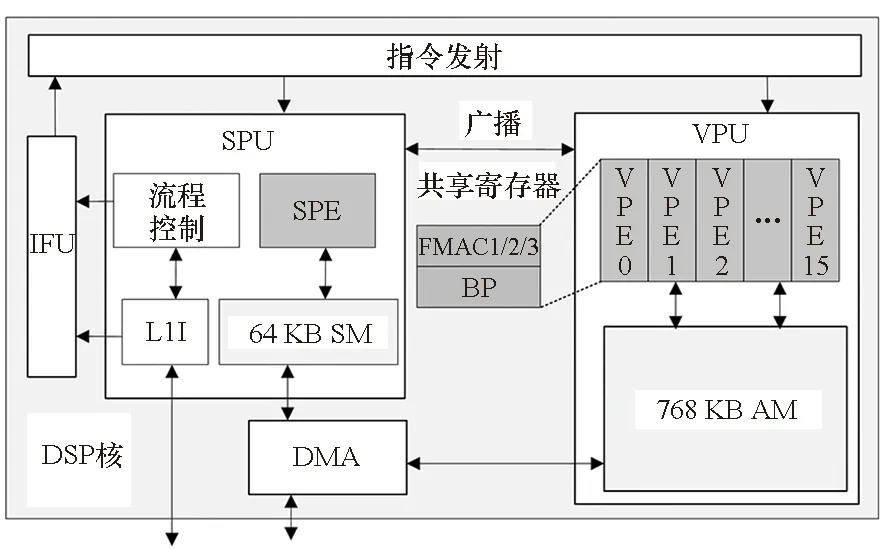
3 面向FT-M7032的矩阵乘卷积实现分析
4 面向多核DSP的矩阵乘卷积算法优化
4.1 ftmEConv算法整体设计

4.2 输入特征图转换

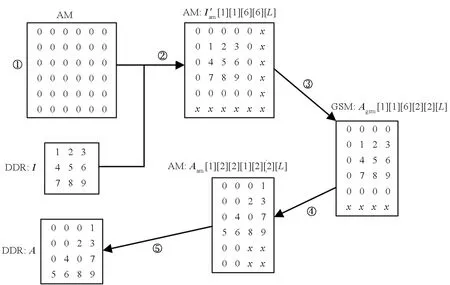
4.3 卷积核转换

4.4 矩阵乘
4.5 输出特征图转换

5 性能评估
5.1 实验设置
5.2 ftmEConv的开销剖析
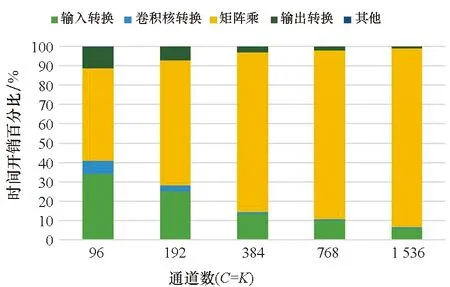
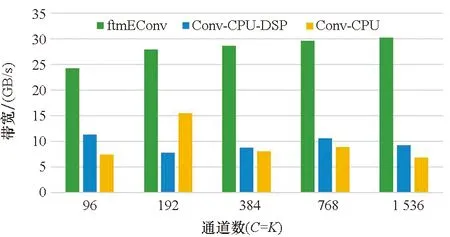
5.3 不同实现的性能对比

5.4 在典型网络上的性能测试
6 结论

