考虑多性能参数的引信弹簧可靠性评估*

杨承强，顾晓辉，潘守华

(1. 南京理工大学 机械工程学院， 江苏 南京 210094； 2.北方特种能源集团西安庆华公司， 陕西 西安 710025)

引信是弹药实现有效毁伤目标的关键组件，其可靠性失效不仅会耽误战机甚至可能造成人员伤亡。弹簧作为一种常用的储能元件，在引信中主要起到限制隔爆件运动或为击针运动提供能量的作用，是影响引信可靠性的重要零件。根据在引信中作用效果的不同，弹簧主要有三种失效模式：疲劳断裂、应力过强和应力松弛[1]。

国内外众多学者对弹簧的可靠性进行了许多研究[2-3]。Manouchehrynia等[2]以汽车螺旋弹簧在随机载荷下的疲劳可靠性预测为基础，提出了一种估计应变寿命的概率模型，能有效预测弹簧的疲劳寿命；Ceyhanli等[4]对重型汽车的抛物线板簧静强度和疲劳寿命可靠性进行了试验和数值分析，得出该板簧在车辆试用期间可以安全使用的结论；付涛等[5]对高服役应力弹簧进行了疲劳试验，并提出了一种基于支持向量机的弹簧疲劳寿命威布尔可靠性分析方法；王建平等[6]在不同温度和初始载荷下对斜圈弹簧进行了加速退化试验，并将Arrhenius方程理论与应力松弛理论相结合，研究弹簧参数与其寿命的关系。目前弹簧的可靠性评估大多针对工作状态下的弹簧，而引信弹簧大部分时间处于贮存状态。虽然有涉及弹簧贮存寿命的研究，但缺少对其贮存期间可靠度变化的预估。当前弹簧可靠性的研究往往只考虑应力损失率，缺乏对弹簧其他性能参数的考虑。弹簧作为高可靠性、长寿命产品，若只考虑单一性能参数，在进行试验时，获得的退化数据往往过少，导致可靠度评估结果不准确。

针对上述问题，本文提出一种基于修正Arrhenius模型的弹簧多元可靠性评估方法，以恒定应力加速退化试验为手段，考虑弹簧多个性能参数，并根据修正的Arrhenius方程获得贮存温度下的退化轨迹曲线，同时采用Anderson-Darling统计量检验退化量的分布，建立基于多元正态分布的可靠度模型，通过与其他可靠度模型的对比，验证了该方法的准确性。

1 试验方案设计

1.1 试验对象

试验对象为引信圆柱螺旋弹簧，其长度为17.5 mm，线径为0.40 mm，外径为4.05 mm，节距为1.9 mm，采用轴向安装方式，安装后的装配长度为5.8 mm。

1.2 试验应力与样本量的选择

实践经验[7-8]表明，该弹簧在随引信贮存时，热应力是影响其性能退化最主要的因素，因此本试验选择温度作为试验加速应力。加速应力的选择应遵循最高试验温度下与贮存温度下失效机理保持一致的原则[9]。该材料的弹簧工作温度范围理论上为-100～200 ℃，因此最高试验温度确定为160 ℃。基于统计分析和试验成本的考虑，设置4个试验应力水平数，分别为T1=120 ℃、T2=130 ℃、T3=150 ℃、T4=160 ℃。

从理论上讲，样本量越大，最后估计的结果也越准确。但样本量太大，会导致试验成本(时间成本和人力成本)大大增加。经综合考虑，在每个试验温度下投入8个样本，共n=32个样本。

1.3 性能退化参数与失效阈值的确定

1.3.1 应力损失率

弹簧常用的性能退化参数是应力损失率[10]，其定义为：

(1)

式中：δ为应力损失率，Pt为试验后的弹簧弹力，单位为N；P0为弹簧初始弹力，单位为N。

供应方所给弹簧的规格要求规定了弹簧安装后的弹力范围，经计算应力损失率后考虑到安全性，向下取整得到失效阈值为7%。

1.3.2 永久变形率

弹簧应力松弛过程从宏观角度出发实际上是一个由弹性应变向塑性应变转换的过程[11]。在应力松弛过程中，弹性应变εe和塑性应变εp的和为一个常数c，即：

εe+εp=c

(2)

因此，选择永久变形率作为另一个退化性能参数，其定义为：

(3)

式中：ε为永久变形率；Lt为试验后弹簧的长度，单位为mm；L0为弹簧初始长度，单位为mm。

根据摸底试验，将ε=5%作为永久变形率的失效阈值。

1.4 试验检测时间

有试验表明[12]，弹簧前期退化快，后期退化慢。因此，为更好拟合弹簧的退化轨迹曲线，前期检测频率高，然后检测频率慢慢降低。具体的检测时间见表1。

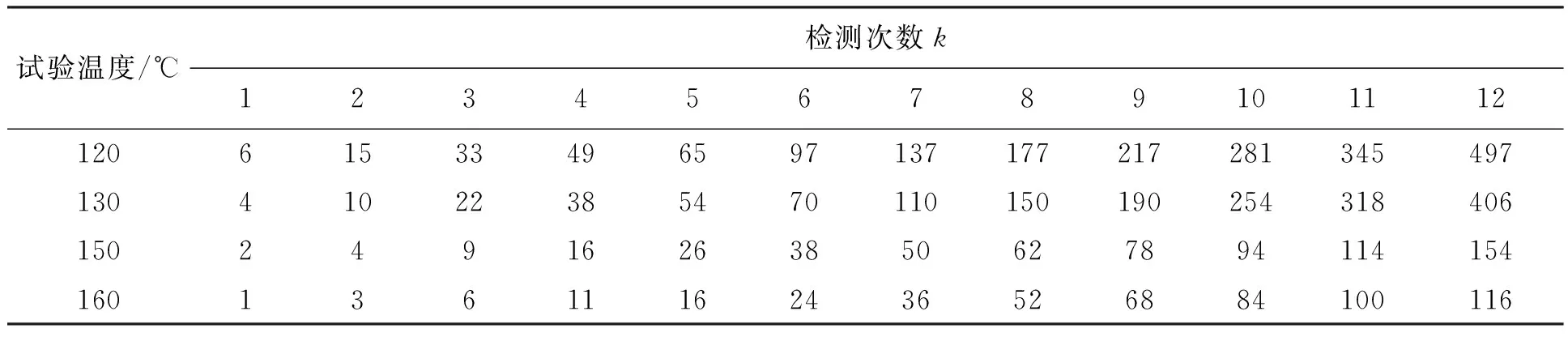
表1 性能参数检测时间Tab.1 Degradation parameters detection time h

1.5 试验设备

恒温干燥箱(XMTD-9000，DHG型恒温数显干燥箱)1台、数显式压力仪(精度为0.1 N)1台、视频显微镜1台、台式计算机1台和游标卡尺1把。

试验设计了专用安装夹具，共32个。夹具材料为LC4硬铝材料，其由套筒、盖板、螺栓、螺母和防松垫圈组成，如图1所示。套筒内径略大于弹簧外径，盖板下侧有一圆形凹槽，直径与弹簧外径相等，起固定弹簧的作用。该安装方式能最大程度上模拟弹簧在引信中真实的安装状态。套筒的槽深为夹具关键尺寸，该尺寸采用精加工以减小夹具不同而产生的差异。

图1 夹具与安装Fig.1 Fixture and installation

1.6 数据测量

从同一生产批次的圆柱螺旋弹簧中，随机抽取32个，平均分为4组分别放入120 ℃、130 ℃、150 ℃、160 ℃的恒温干燥箱中，按表1中的时间取出，并在室温下冷却3 h后进行测量[13]。

弹簧应力用数显式压力仪进行测量。先寻找弹簧压缩的起始点，然后将弹簧置于测量夹具中，使测量探头压缩弹簧到规定值，然后读取稳定显示的压力读数。

弹簧长度采用计算机视觉的方法测量。将弹簧置于游标卡尺上，然后用视频显微镜进行拍照。在台式计算机上打开长度测量程序，先进行长度标定(标定距离为15 mm)，然后选取弹簧两端即可得到其长度，最后通过重复测量取均值来减小人为误差。该测量方法的精度达0.001 mm。

1.7 数据处理

按式(1)和式(3)计算每个样品在各检测点的应力损失率δ和永久变形率ε，其退化曲线如图2所示。

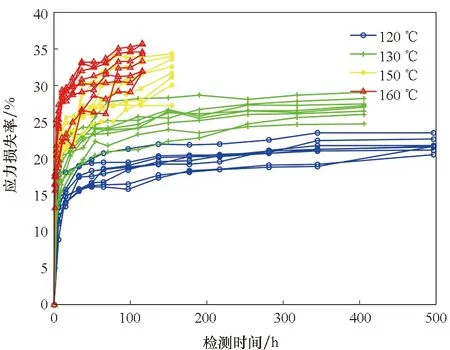
(a) 应力损失率(a) Stress loss rate

(b) 永久变形率(b) Permanent deformation rate图2 性能参数退化曲线Fig.2 Performance parameter degradation curve

检验加速应力下贮存失效机理的一致性，相当于检验退化轨迹曲线的形状是否近似[14]。从图2可以看出两个性能参数在各加速应力下的退化轨迹曲线是相似的，并且通过计算Spearman秩相关系数可验证该结论。

2 基于修正Arrhenius模型的回归分析

2.1 性能退化轨迹方程

经分析可知[15]，弹簧的两个性能退化过程可表达为：

yz=azln(t)+bz

(4)

式中：yz为弹簧第z(z=1,2)个退化过程的退化量；az为第z个退化过程的退化速率；bz为第z个退化过程的模型常数；t为退化时间，单位为h。

(5)

式中：yijzk为第i(i=1,2,3,4)个应力水平下第j(j=1,2,…,8)个样本第z(z=1,2)个退化过程第k次检测的退化数据。

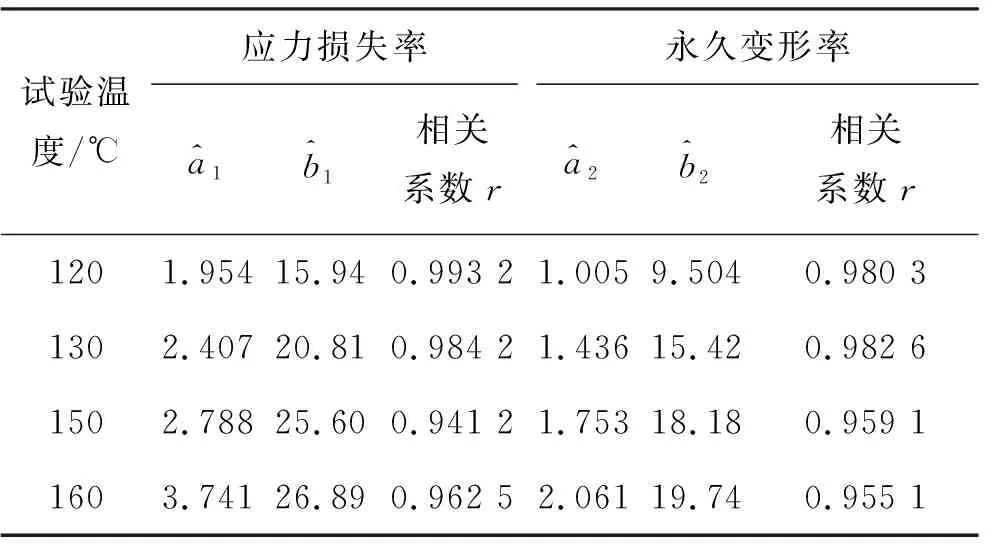
表2 退化轨迹模型的参数估计值Tab.2 Parameters estimate of degradation curve model

设显著水平为0.01，查相关系数临界表得r0.01=0.834 0。表2中的相关系数均大于0.834 0，因此4组退化轨迹方程的线性回归效果显著。

2.2 修正Arrhenius模型

由于加速应力为热应力，所以加速模型首选Arrhenius模型，即：

(6)

式中：a为退化速率；A为Arrhenius常数；Ea为活化能；T为绝对温度；R为玻尔兹曼常数。

数据分析时，发现反应速率a与1/T并不是一条很好的直线。经研究后得知[16]，这是由于Arrhenius模型的前提假设认为活化能Ea是与温度无关的常数，这在一定温度范围内是正确的。然而大量实践表明[17-18]，对于温度范围较大或较复杂的反应过程，活化能Ea与温度T有关。 因此，采用修正的三参数Arrhenius模型作为加速模型[19]：

(7)

式中：E0为试验活化能，与温度无关；m是[-2,2]之间的整数或半整数。

对式(7)两边取对数，并令Y=lna，c=ln (A)，d=-E0/R，可得：

Y=c+mlnT+d/T

(8)

(9)

经计算得到性能参数退化速率的加速方程。此时，退化速率的残差平方和分别为I1=0.015 2、I2=0.017 6。

a1=exp(-7.118+2lnT-1 631/T)

(10)

a2=exp(-6.857+2lnT-1 969/T)

(11)

式中：a1和a2分别是应力损失率和永久变化量的退化速率。

式(4)中的b可以看作1 h后的退化量，根据修正的Arrhenius方程可得：

(12)

采用上述同样方法，可得：

b1=exp(22.33-2lnT-2 971/T)

(13)

b2=exp(23.54-2lnT-3 618/T)

(14)

此时，残差平方和分别为I3=0.010 7，I4=0.051 0。

贮存弹药的库房一般会严格控制温度，因此设弹簧随引信贮存的环境温度为T0=25 ℃，按式(10)、式(11)、式(13)、式(14)可计算出弹簧在贮存温度T0下性能参数的退化轨迹方程，并得到在25 ℃下弹簧的性能退化曲线，如图3所示。

图3 在25 ℃下弹簧的退化轨迹曲线Fig.3 Degradation trajectory curve at 25 ℃

μ1=0.302 5ln(t)+2.640

(15)

μ2=0.126 0ln(t)+1.001

(16)

式中：μ1和μ2分别表示应力损失率的退化均值和永久变形率的退化均值；t为弹簧贮存时间，单位为h。

3 多性能参数的可靠性评估

根据修正的Arrhenius方程外推获得弹簧在温度T0=25 ℃下的退化轨迹方程，由此就可预估弹簧在贮存期间的可靠度变化。

3.1 退化量分布的检验

正态分布和威布尔分布是可靠性评估中最常用的分布类型。采用Anderson-Darling(AD)检验[20]，对不同试验温度Ti下样品性能参数的退化量分布进行拟合优度检验。应力损失率δ和永久变形率ε的AD统计量和p值的计算结果分别见表3和表4。

表3 应力损失率的AD检验Tab.3 AD test of stress relaxation rate

表4 永久变形率的AD检验Tab.4 AD test of permanent deformation rate

表3和表4中的p值均大于显著水平0.05，并且应力损失率和永久变形率的正态分布AD统计量均值为0.349 4和0.387 3，分别小于其威布尔分布的AD统计量均值0.419 2和0.468 5，所以样品应力松弛和永久变形退化数据的最优分布均为正态分布，即：

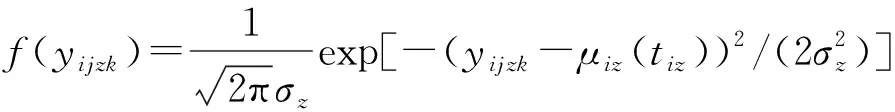
(17)

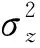
3.2 基于二元正态分布的可靠度模型

记Y=(δ,ε)T表示弹簧性能参数向量，根据退化量分布检验的结果，可得应力损失率和永久变形率两个性能参数的向量服从二元正态分布，即：

(18)

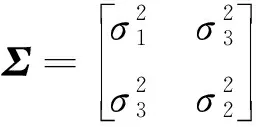
Cov(yZ,yz)=E[(yZ-E(yZ))(yz-E(yz))]

(19)

按式(19)计算性能参数退化数据的协方差为：

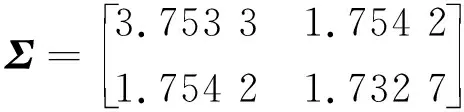
(20)

在给定性能参数失效阈值的情况下，对式(18)积分可以得到弹簧在t时刻的可靠度模型，即：

Rr(t)=P[δ≤7,ε≤5]

(21)

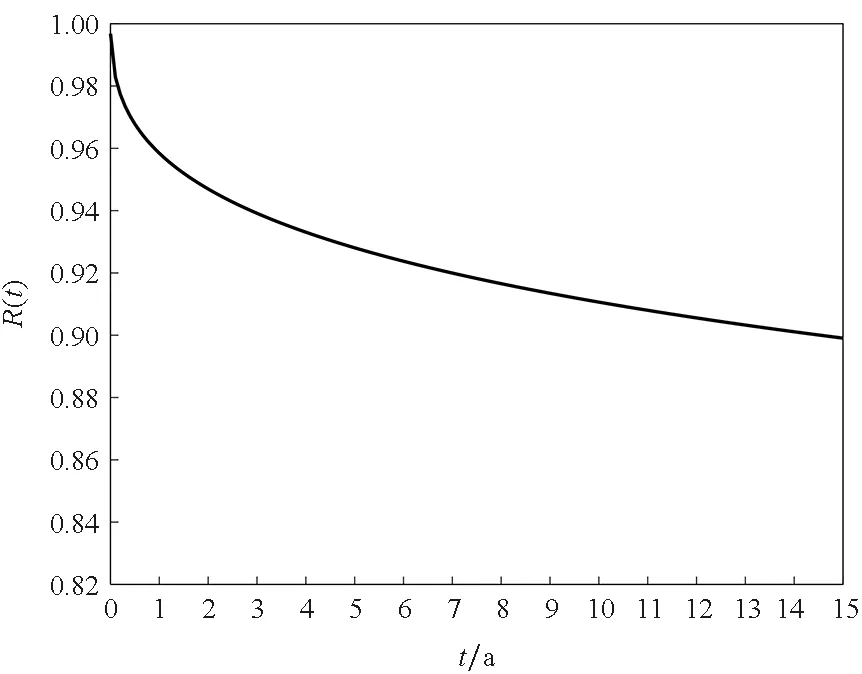
由此，根据式(21)给出在15 a内弹簧的可靠度随贮存时间的变化，如图4所示。

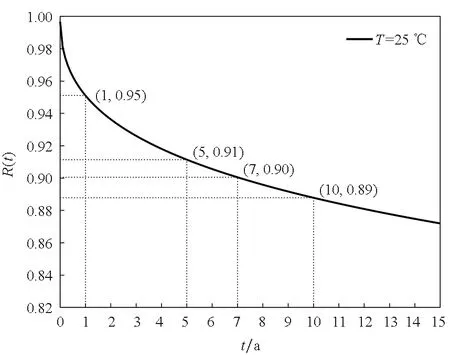
图4 双参数相关的可靠度曲线Fig.4 Two-parameter reliability curve

从图4可知，该弹簧贮存1 a后，其可靠度从1降到0.95左右，之后进入缓慢退化阶段。当可靠度为0.90时，该弹簧的贮存寿命为7 a，基本满足引信贮存需要。在贮存7 a后，维护人员需密切关注引信中弹簧的性能退化情况，及时采取相应的处理措施。

可靠度分析情况如图5所示。从图5中可以看出，弹簧在T0=25 ℃下贮存时，其可靠度曲线不同于一般的可靠度曲线(S形曲线，分为平稳期—速降期—平稳期)，而是L形曲线(速降期—平稳期)。①弹簧的性能失效阈值较低，通常都在10%以下，远低于其他产品的失效阈值(如橡胶圈的失效阈值在30%左右)，这导致退化量分布离阈值近，所以弹簧一开始就是速降期；②在贮存初期，弹簧退化速率快，但持续时间短，所以其可靠度曲线的速降期时间也很短；③该引信弹簧个体差异较大(退化量方差较大)，而且退化到一定程度后开始非常缓慢地退化，所以其可靠度曲线的平稳期非常长，并且可靠度几乎永远不会到0。

(a) 弹簧的可靠度分析(a) Spring reliability analysis

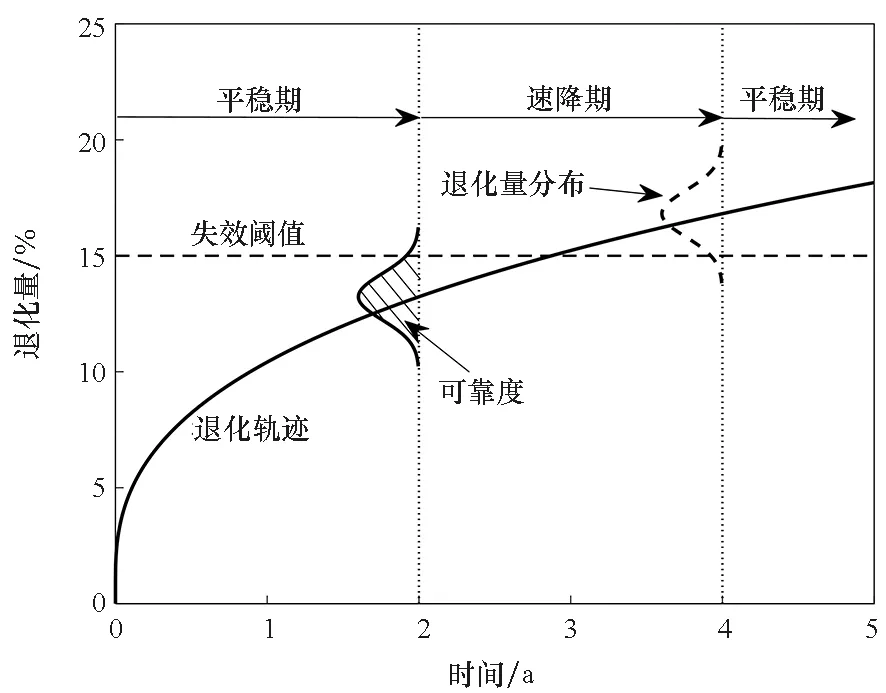
(b) 其他产品的可靠度分析(b) Other product reliability analysis图5 可靠度分析Fig.5 Reliability analysis

4 评估结果分析

若只将应力损失率作为性能参数，根据式(15)、式(17)、式(20)可以得到应力损失率δ的可靠度模型：

(22)

式中：Φ(·)表示标准正态分布的累积概率函数。

由此，根据式(22)可以得到弹簧应力损失率的可靠度曲线，如图6(a)所示。

(a) 应力损失率(a) Stress loss rate

(b) 永久变形率(b) Permanent deformation rate

(c) 两者独立(c) Both independent图6 可靠度曲线Fig.6 Reliability curve

若只将永久变形率作为性能参数，根据式(16)、式(17)、式(20)可以得到永久变形率ε的可靠度模型：

(23)

由此，根据式(23)可以得到弹簧永久变形率的可靠度曲线，如图6(b)所示。

当应力损失率和永久变形率互相独立时，根据式(22)、式(23)可以得到在两者独立情况下的弹簧可靠度模型：

Rv(t)=Rs(t)·Rt(t)

(24)

根据式(24)可以得到弹簧两个性能参数独立时的可靠度曲线，如图6(c)所示。

通过上述讨论，可以比较弹簧应力损失率的可靠度Rs(t)、永久变形率的可靠度Rt(t)、两者独立时的可靠度Rv和两者相关时的可靠度Rr，曲线对比如图7所示。

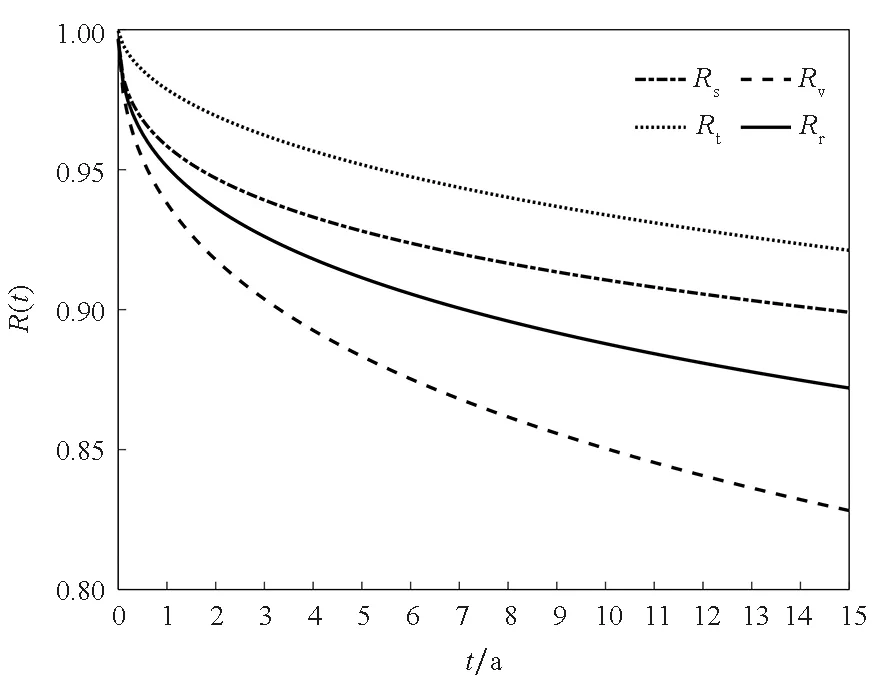
图7 可靠度曲线对比Fig.7 Reliability curve contrast

从图7可以看出，不论哪个可靠度曲线，其共同特点是：前期可靠度快速下降，后期缓慢下降。因此，为了更好保证引信可靠性，建议对采购的弹簧进行环境试验筛选，避免给引信装配性能退化过快的弹簧，从而降低引信故障率。

对比双参数相关的可靠度Rr与单参数的可靠度Rs和Rt可以看出，用单参数的可靠度会高估弹簧贮存期间的可靠性，所估计的弹簧贮存寿命偏长，这将导致维修不及时，可能造成安全隐患。

对比双参数相关的可靠度Rr与双参数不相关的可靠度Rv可以发现，两个参数独立会明显低估弹簧贮存期间的可靠性，导致引信提早更换，造成资源浪费，降低经济效益。考虑相关性后的可靠度Rr更加接近工程实际。

综上可得，本文的可靠度模型相比其他模型可以较准确地预估弹簧贮存期间的可靠度变化，不仅能提高引信的安全性，而且考虑了其经济性。

5 结论

1) 通过恒定应力加速退化试验，获得弹簧应力损失率和永久变形率的退化数据，并对数据展开统计分析，利用修正的Arrhenius方程进行外推计算，得到弹簧在贮存温度T0=25 ℃时的退化轨迹。

2)采用Anderson-Darling统计量验证样品退化量最优分布为正态分布，并基于二元正态分布得到弹簧双参数相关的可靠度模型。

3) 通过与其他可靠度模型对比，表明本文建立的可靠度模型能更好地反映弹簧实际的可靠度变化，对研究弹簧在贮存条件下的可靠度具有一定的参考价值与指导意义。