广义S变换和阈值分割联合抗频谱扩展-压缩移频干扰*

李 欣，罗富友，袁 天

(中国人民解放军31203部队， 广东 广州 510000)

线性调频 (linear frequency modulation, LFM)信号具有大时宽带宽积特性，有效地解决了雷达作用距离和距离分辨率的矛盾，并且通过接收时的相参处理，降低了非相参干扰的干扰效果，在现代雷达系统中得到了广泛的应用[1]。移频干扰利用LFM信号的距离-多普勒耦合特性，通过对雷达信号进行频率调制，来产生超前或滞后的假目标，是一种有效的相参欺骗干扰样式[2]。

固定移频干扰在对抗LFM信号时，由于频移量固定，频移特征会被雷达用于干扰识别和对抗。针对固定移频干扰的这一缺陷，在当前研究中，提出了步进移频干扰[3]、随机移频干扰[4]、N阶频谱扩展-压缩(spectrum spread and compression， SSC)盲移频干扰[5-7]等干扰样式。这些改进的移频干扰样式针对固定移频干扰易被雷达识别的缺陷，通过增加干扰特征的复杂度，提高了雷达进行干扰识别和对抗的代价，尤其是文献[8]中提出了一种特征隐藏的固定移频干扰方法，进一步增加了干扰对抗的难度。

与移频干扰技术的蓬勃发展相反，移频干扰的对抗技术呈现出一定的滞后性，文献[9]提出利用移频干扰信号中心频率的变化，补偿移频所引起的距离偏差，从而得到目标的真实距离，但是只适用于对抗固定移频干扰，并且对文献[8]中的移频特征隐藏干扰无效。文献[10]提出构建过完备原子库，利用稀疏分解实现对移频干扰的抑制，但是当干扰与回波信号在时间上重叠时，该方法无法重构回波信号，并且改进的多次移频干扰在频移原子中的非稀疏性，也导致该方法失效。文献[11]提出了基于盲源分离和脉冲分集的移频干扰对抗方法，但是盲源分离方法需要多通道雷达来满足盲源分离中的列满秩条件，而脉冲分集方法会增加雷达信号发射和处理的难度。文献[12]根据干扰信号和回波信号时频特征的差异，利用经典脉冲压缩方法和简明分数阶傅里叶变换，提出了经典时频相关移频干扰识别方法和尺度时频相关移频干扰假目标识别方法，在干信比大于0 dB、移频量大于瞬时带宽的15%时，对假目标识别正确率接近100%，但该方法只能用于对抗基本移频干扰，对改进的移频干扰技术无效。文献[13]针对不具备调频斜率捷变的LFM脉冲多普勒雷达，提出利用真实回波、移频干扰相参积累和二维分数阶傅里叶变换峰值差异，对干扰进行鉴别的方法，但该方法在目标存在加速度时，对干扰的识别准确率下降，且同样不适用于改进的移频干扰技术。文献[14]提出通过正交极化辅助天线扩展接收通道，利用盲源分离算法对干扰信号和回波信号进行分离，而后通过频率鉴别的方法识别干扰和回波，但该方法对硬件有一定要求，且盲源分离算法计算量较大。文献[15]提出在两个相邻发射脉冲间进行调频斜率抖动调制，利用调频斜率抖动后，假目标峰值距离变化而真实目标峰值不变的特性，实现对干扰的鉴别，但该方法增加了信号处理的复杂度，且只适用于抑制单假目标干扰，当假目标数量较多时，很难利用峰值距离的变化将假目标全部鉴定出来。文献[16]提出运用盲源分离与卷积神经网络组合抗主瓣干扰，但该方法对样本和计算量具有较高的要求。文献[17-20]中，Ge等运用盲源分离方法与分布式雷达、数字阵雷达和极化多通道雷达等新体制雷达结合实现对雷达主瓣干扰的抑制，文献[21]在多基地雷达系统中提出使用相关聚类的方法实现欺骗干扰的抑制，文献[22]在FDA-MIMO雷达中提出使用协方差矩阵重构的方法来抑制距离假目标，但以上方法均需要满足相应的硬件需求。

N阶SSC盲移频干扰无须估计雷达信号的调频斜率，仅通过控制时延即可实现盲移频干扰，可以对抗脉冲调频斜率捷变雷达，具有较强的工程应用价值。本文首先分析N阶SSC移频干扰的干扰原理，之后根据干扰信号与回波信号在时频分布特征的差异，利用图像处理中的阈值滤波方法构建时频滤波器，实现对干扰的抑制。

1 N阶SSC盲移频干扰的原理

假设雷达发射的幅度归一化LFM信号为：

(1)

假设目标为点目标，所在距离为R，则回波信号波形可表示为：

jπK(t-tr)2]

(2)

式中，tr=2R/c，c为光速。

设雷达发射信号为正调频信号，并且产生的假目标超前于真实目标，则N阶SSC干扰信号可表示[5]为：

sj(t)=[s(t-tr-td)]N[s*(t-Δt-tr-td)]N-1

exp{j2π[f0+(N-1)KΔt](t-tr-td)+

jπK(t-tr-td)2+jΔφ}

(3)

式中，Δφ=2π(N-1)f0Δt-π(N-1)KΔt2，N为频谱扩展的阶数，Δt为干扰产生时所设定的延时，td为干扰机转发的系统延时。

该干扰的原理如图1所示。

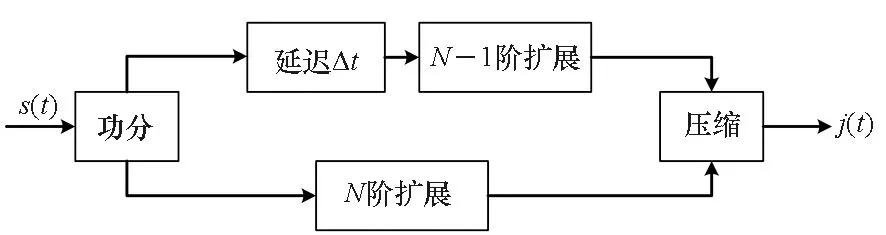
图1 N阶SSC移频干扰产生原理Fig.1 Schematic diagram of Nth order SSC shift-frequency jamming

雷达进行解线调处理时的参考信号为：

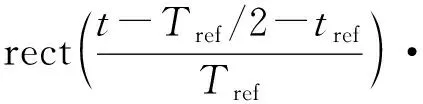
exp[j2πf0(t-tref)+jπK(t-tref)2]

(4)

式中：Tref为接收窗的宽度，通常Tref>T；tref为接收窗的起始时刻。

雷达进行解线调处理实际是将接收信号的共轭与参考信号相乘，经过解线调处理后，雷达信号和干扰信号的表达式为：

exp[-j2πK(tr-tref)t-j2πf0(tr-tref)+

(5)

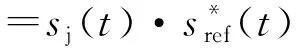
exp{j2πK[tref+(N-1)Δt-(tr+td)]t+jΔφ1}

(6)

式中，

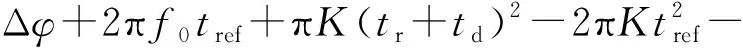
2πf0(tr+td)-2π(N-1)KΔt(tr+td)

根据解线调处理的原理可知，式(5)和式(6)输出频率峰值对应的时刻分别为：

tr=tref-fr_peak/K

(7)

tj=tref-fj_peak/K=tr+td-(N-1)Δt+td

(8)

从式(6)可以发现，若忽略干扰机的系统延时，N阶SSC盲移频干扰引入了(N-1)KΔt的频移量，输出的假目标相对于目标回波的延迟量为(N-1)Δt，即N阶SSC盲移频干扰可以通过控制扩展阶数和时间延迟在固定的位置形成假目标，而常规移频干扰则需要估计雷达信号调频斜率，通过精确控制频移量来实现在预定位置形成假目标，当调频斜率发生变化时，干扰参数也需要相应的变化。同理，滞后假目标干扰的产生原理为：

j(t)=[s(t-Δt-tr-td)]N[s*(t-tr-td)]N-1

(9)

此时，引入的移频量为-NKΔt。

从上述分析可以发现，N阶SSC盲移频干扰无须对雷达参数进行估计，只需要控制延迟时间，即可在预定距离形成假目标，具有较强的灵活性和工程应用价值。但是，根据式(3)可知，干扰信号与雷达信号在脉冲宽度上是失配的，并且N阶SSC盲移频干扰在本质上仍是基于固定移频干扰，即干扰信号与雷达信号存在频率差，这一频率差由脉冲截断的长度来进行控制，避免了对雷达信号调频斜率的估计。

2 基于广义S变换和阈值滤波的干扰抑制方法

根据上一节的分析可知，经过解线调处理后，移频干扰信号与雷达信号存在一个固定的频率差，但是由于目标的距离信息未知，即解线调处理后目标回波对应的频率未知，因此无法利用频域滤波来进行干扰抑制。通常欺骗干扰所形成的假目标的能量高于真实目标回波，即干扰信号在时频图像中将占据强能量区域，因此对接收信号的时频图像进行阈值滤波，可以将回波所占据的时频区域选择出来，进而实现对干扰的抑制。

2.1 基于广义S变换的回波时频图像获取

S变换是由Stockwell在1996年提出的一种具有良好时频聚集性的时频分析方法[23]，并且在随后的研究中，通过对基本S变换的窗函数增加调节因子，改善了S变换的分辨率调节能力，在时频面上表现出更好的能量聚集性和时频分辨能力，这些改进的S变换统称为广义S变换(generalized S transform, GST)[24]。这里选用文献[25]中所提出的GST作为工具来获取时频图像，对于一个确定的信号x(t)，其GST表达式为：

(10)

式中，λ和p为分辨率调整因子。

GST为线性可逆变换，广义S逆变换(inverse generalized S transform, IGST)可表示为：

(11)

雷达接收信号可表示为：

z(t)=sr(t)+aj(t)+w(t)

(12)

式中：a为干信比(jamming to signal ratio, JSR)对应的幅度比；w(t)为接收机内噪声，服从零均值高斯分布。

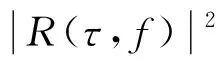
2.2 基于Tsallis交叉熵的分割阈值确定方法

对于得到的灰度图像，需要选择合适的阈值构建时频滤波器，将干扰信号所占据的时频区域分割出来。噪声信号经过解线调处理和GST后，其能量分布于整个时频平面内，并且对应的灰度值也较低。同时，由于干扰能量强于回波能量，因此在进行阈值分割时，可将噪声和回波所占据的时频区域视作背景，图像分割的目标就是寻找最佳阈值将干扰所占据的时频区域从背景中分割出来。

设图像I1的灰度级为L，图像大小为M×M，图像的灰度直方图为H=(h0,h1,…,hL-1)，hi表示图像中灰度值为i的像素值出现的次数，将图像视作一个随机分布，则灰度值为i的像素在图像中出现的概率可表示为：

(13)

式中，Qq(x)=(x1-q-1)/(1-q)。

设t0为一个合适的分割阈值，将图像分为背景区域和干扰区域两部分，分别用C0和C1表示，则C0和C1包含的像素级出现的总概率[27]分别为：

(15)

(16)

同样可得C0和C1对应的平均灰度级为：

(17)

(18)

则C0和C1的广义Tsallis交叉熵为：

(19)

(20)

根据Tsallis交叉熵的伪叠加性，可得阈值分割前后总的Tsallis交叉熵为：

(21)

式中，I2表示分割后的图像。

最佳分割阈值可通过遍历所有的灰度值，计算相应的Tsallis交叉熵，找出最小交叉熵对应的灰度值得到最佳分割阈值为：

Popt=argmin[D(I1|I2)]

(22)

根据计算得到的最佳阈值，即可设计时频滤波器。

(23)

利用得到的时频滤波器对R(τ,f)进行时频滤波，即可滤除干扰对应的能量，之后再进行IGST，得到干扰抑制后的信号，再做快速傅里叶变换(fast Fourier transform, FFT)即可得到脉冲压缩的结果。整个算法的流程如图2所示。

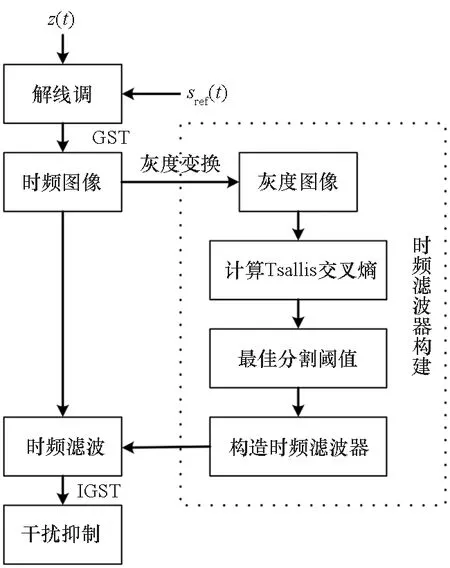
图2 干扰抑制方法流程Fig.2 Flow chart of the jamming suppression method

3 仿真与分析

雷达发射带宽B=10 MHz、脉冲宽度T=50 μs的LFM信号，采样频率fs=20 MHz，则采样点数M=1 000。设干扰信号的频谱扩展阶数为4，假目标相对真实目标的时间差为Δtj=[-20,-10,-5,10,15] μs，则当干信比JSR=20 dB和信噪比SNR=0 dB时，经过解线调处理后，雷达接收信号的脉冲压缩输出如图3所示。

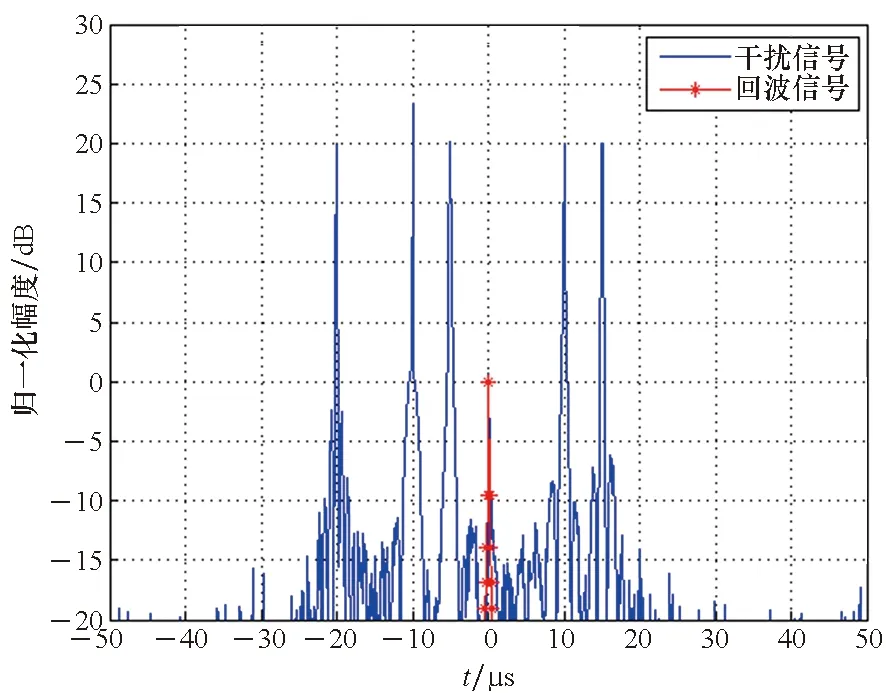
图3 接收信号脉冲压缩结果Fig.3 Pulse compression result of received signal

从图3可以发现，经过脉冲压缩后，N阶SSC移频干扰可以在预设的时刻形成假目标，并且假目标的峰值远高于真实目标，使雷达无法识别真实目标。

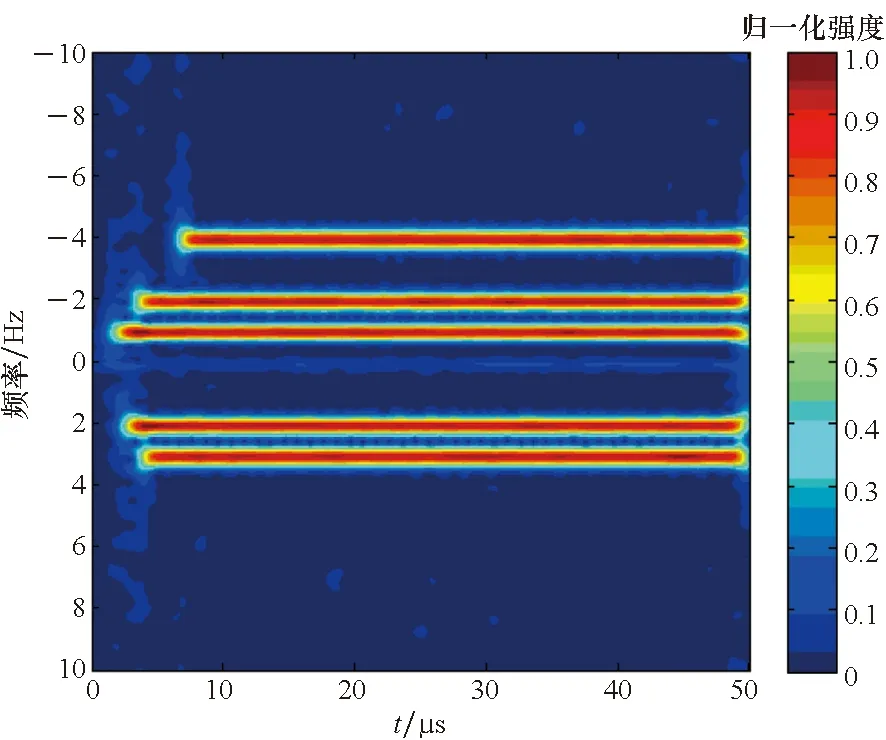
取λ=0.09和p=0.11，则雷达接收信号做GST后对应的时频图像和灰度图像如图4所示。灰度图像对应的灰度直方图如图5所示。

(a) 时频图像(a) Time-frequency image

(b) 灰度图像(b) Gray level image图4 接收信号的时频图像和灰度图像Fig.4 Time-frequency and gray level images of received signal

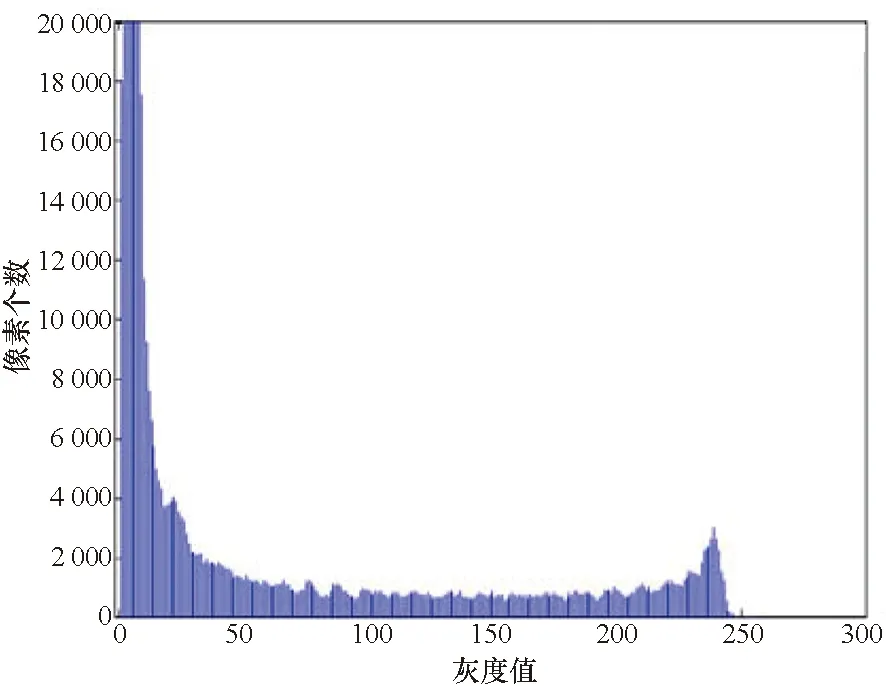
图5 灰度图像对应的灰度直方图Fig.5 Grey level histogram of gray level image

根据图像的灰度直方图，遍历所有灰度值对应的Tsallis交叉熵，搜索交叉熵最小值对应的灰度值即可得到最佳分割阈值，交叉熵的计算结果如图6所示。

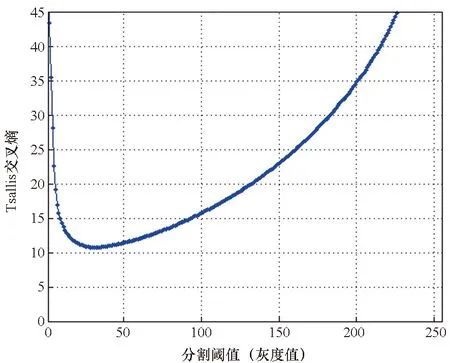
图6 不同分割阈值的Tsallis交叉熵Fig.6 Tsallis cross entropy of different segment thresholds

根据灰度直方图可以发现，灰度直方图表现出一定的双峰特性，但是其谷底较为平坦，不能直接应用双峰特性来选择阈值。应用基于Tsallis交叉熵的阈值分割方法计算得到的阈值Popt=31，即以灰度值31作为分割阈值来构建时频滤波器，将大于该阈值的时频区域滤除。滤波后的时频图像如图7所示。

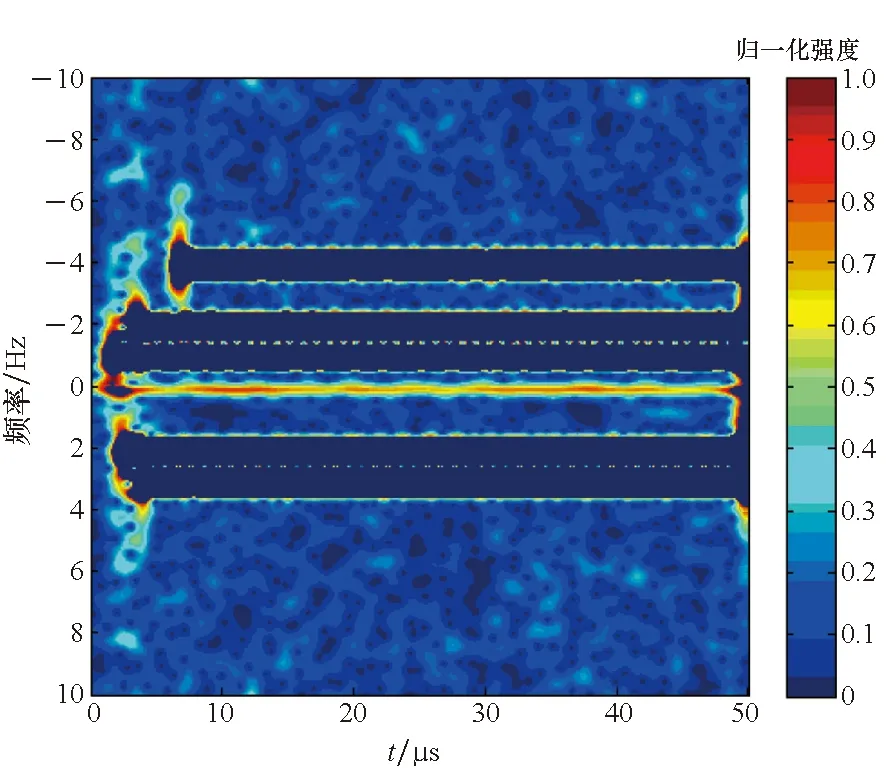
图7 阈值滤波后的时频图像Fig.7 Time-frequency image after threshold filtered

从图7可以发现，经过阈值滤波后，干扰信号所占据的时频区域已经被滤除，目标回波所占据的时频区域在图像中已经较为明显。对图7做IGST和FFT即可得到干扰抑制后的脉冲压缩结果，如图8所示。

图8 干扰抑制后的脉冲压缩输出Fig.8 Pulse compression result after jamming suppression

从图8可以发现，经过阈值滤波后，干扰信号所形成的假目标已经得到了抑制，与图3相比，在原来假目标所在距离单元，干扰抑制比可达30 dB以上，表现了较好的干扰抑制效果。

为了定量评估所提方法的抗干扰效果，这里引入相似系数和信干噪比(signal-to-interference and noise ratio, SINR)增益。相似系数的定义为：

(24)

式中，x(n)和y(n)为两个离散向量。

相似系数反映了两个向量的相似程度。根据式(5)可知，经过解线调处理后，回波信号为一个单频信号。以经过解线调处理后的信号为研究对象，计算干扰抑制前后的信号与式(5)的相似系数。根据干扰抑制的原理，干扰被抑制后，输出信号中应当主要由回波信号、噪声和剩余干扰信号组成，如果干扰抑制效果较好，则输出信号与式(5)的相似程度会提高。经过解线调处理的信号在干扰抑制前后与理论信号的相似系数如图9所示。

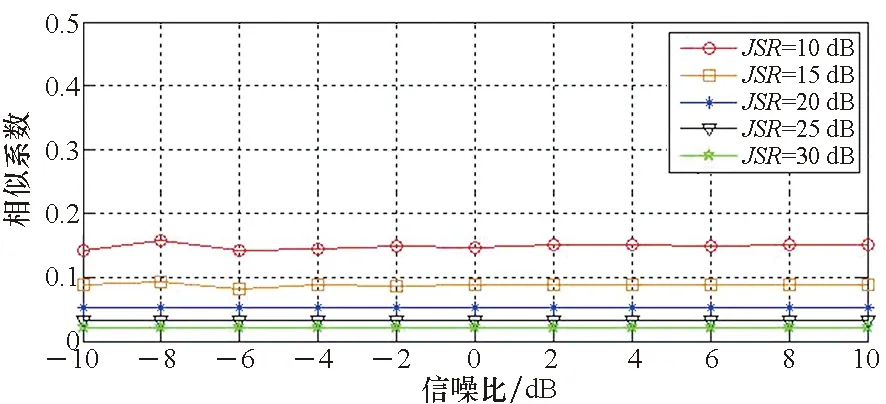
(a) 干扰抑制前相似系数(a) Similarity coefficient before jamming suppression

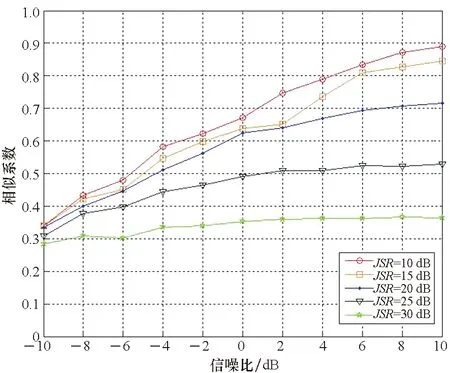
(b) 干扰抑制后相似系数(b) Similarity coefficient after jamming suppression图9 干扰抑制前后相似系数Fig.9 Similarity coefficient before and after jamming suppression

从图9可以发现，在干扰抑制前，输入信号与理论信号的相似系数都比较小，且干信比越大，输入信号中回波信号所占成分越少，相似系数越小；经过干扰抑制后，相似系数有了明显的提高，表明输出信号中，回波信号所占成分有了提高，体现了该方法对干扰的抑制效果。需要注意的是，干信比越小，经过干扰抑制后的相似系数越大，主要原因是由于这种情况下，干扰本身能量较低，经过时频滤波后，剩余干扰信号成分较少，对应的相似系数就越高。

但是单纯根据相似系数无法确定干扰抑制的效果，因此这里定义信干噪比增益为RG=SINR2-SINR1，SINR1表示抑制前的信干噪比，SINR2表示抑制后的信干噪比，均以dB为单位，则干扰抑制前后，信干噪比增益随信噪比的变化曲线如图10所示。

图10 信干噪比增益变化曲线Fig.10 Curve of the SINR gain

从图10可以看出:

1)随着信噪比的增加，信干噪比增益也逐渐提高，并且信干噪比增益数值较大，表明该方法具有较好的抗干扰效果。以前面仿真时所取的参数为例，JSR=20 dB和SNR=0 dB时，对应的信干噪比增益为26 dB左右，输出相似系数为0.65左右，此时干扰已经得到了很好的抑制。

2)当JSR≥20 dB和SNR≥0 dB时，信干噪比的增加已经不再明显，这主要是因为此时噪声相对于干扰来说，能量很小，所以在计算信干噪比时，主要取决于干扰抑制前后干扰的能量。

同时也注意到，在JSR≥20 dB和SNR≥5 dB时，该方法的信干噪比增益基本不随干信比变化而变化，以JSR=30 dB和SNR=10 dB时的输出信号来分析，输出信号对应的时频图像如图11所示。

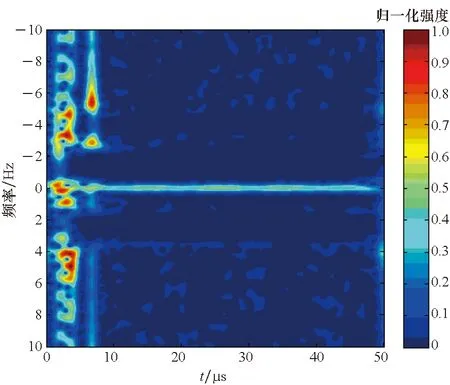
图11 输出信号的时频分布Fig.11 Time-frequency distribution of the output signal

从图11可以发现，经过时频滤波后，回波信号在时频图像中已经很明显地显示出来，表明此时仍有较好的抗干扰效果。但是从时频图像中可以发现，在图像左侧，有一些孤立的强能量点，其信号强度约为回波信号强度的2～3倍，对应的是干扰信号在时频图像中的边缘部分。这主要是由于GST为线性变换，本质上仍受限于不确定性原理，在边缘处时频聚焦性较差，导致时频滤波方法在边缘部分无法将干扰滤除。

4 结论

1)SSC移频干扰无须估计雷达信号调频斜率参数和精确设置干扰移频量，仅通过时延控制和乘法运算即可产生超前和滞后的假目标，具有较好的灵活性。

2)广义S变换具有较好的时频聚焦性，解线调处理的干扰信号和回波信号经过GST处理，在时频平面上具有明显的差异，这一差异为抗干扰提供了理论支撑。

3)基于Tsallis交叉熵的阈值分割方法具有较强的稳健性和较大的适用范围，对于JSR∈[10,30] dB的干扰都具有良好的抑制效果，干扰抑制比可达30 dB以上。

4)基于全局阈值分割和时频滤波的方法无法很好地滤除时频图像中的边缘部分，在后续研究中，应当引入局部阈值分割的方法，进一步提高干扰抑制的效果。

本文所提方法对于SSC移频干扰具有较好的抑制效果，并且从原理上对于常规的移频干扰也具有同样的对抗效果。但是该方法从本质上说，是基于干扰信号和回波信号在时频域的能量不同引起的灰度值差异来进行滤波器设计，当二者能量较为接近时，基于全局阈值滤波的方法将难以有效抑制干扰。针对这一不足，后续需要改进分割阈值获取算法或引入局部阈值分割的方法来进一步提高干扰抑制的效果。