基于频谱扩展-压缩(SSC)的移频干扰分析
徐志朝,张培瑶,姜 淼,刘 伟,曾大治
(北京理工大学,北京 100000)
电子对抗专题 doi:10.3969/j.issn.1673-5692.2016.05.002
基于频谱扩展-压缩(SSC)的移频干扰分析
徐志朝,张培瑶,姜 淼,刘 伟,曾大治
(北京理工大学,北京 100000)
欺骗干扰一般通过模拟雷达目标信号特征,使雷达获得假信息而丢失真实目标信息,达到欺骗目的。移频干扰作为欺骗干扰的一种产生方式,可以弥补延时转发式干扰在面对重频参差雷达、步进频雷达等新体制雷达时无法产生稳定前移假目标的缺点,而常规移频干扰必须了解被干扰雷达的调频斜率等先验知识,使其在面对调频斜率捷变雷达时,不能产生理想的欺骗干扰效果。本文主要阐述一种新的移频方式以及利用MATLAB分析其干扰原理及效果。
移频干扰;频谱扩展-压缩;调频斜率先验知识
0 引 言
欺骗干扰一般通过模拟雷达目标信号特征,使雷达获得假信息而丢失真实目标信息,达到欺骗目的。欺骗干扰的产生一般通过延时转发或者移频产生,以上两种方式的优点在于实现方法相对简单,而移频干扰主要是为了弥补延时转发式欺骗干扰不易产生前移假目标的缺点,但随着步进频雷达以及频率捷变雷达的出现,常规移频干扰很难产生有效地前移假目标,下面将通过常规移频干扰和基于频谱扩展-压缩(SSC)移频干扰的对比分析,验证SSC移频干扰可以在不获取雷达调频斜率前提下,产生有效的欺骗干扰。
1 普通移频干扰
线性调频信号在距离和速度间存在着强耦合,当信号具有多普勒频移时,压缩信号的主峰出现时间会相对无多普勒频移时超前或滞后,即可借助频率移动的手段,达到距离移动的目的,这构成了对线性调频雷达移频干扰的基础。
1.1 移频干扰原理分析
雷达在距离向发射线性调频信号,设雷达发射的线性调频信号表达式为:
式中:A0为信号幅度;fc为信号载频;Kτ为信号的调频率。首先分析匹配滤波器对不同多普勒频移的影响。在没有多普勒频移时,信号复包络为p(t),匹配滤波器的输出响应为:
当有多普勒频移时,其复包络为p(t)ej2πfdt,这时滤波器输出为:
式中:y(τ,fd)为模糊函数的一种定义方式。
为了研究的方便,设线性调频信号归一化包络为:
根据上式可得线性调频信号的模糊函数为:

1.2 移频干扰对雷达的影响
1.2.1 移频量与搬移距离之间的关系
移频造成的延时与移频量之间的关系为:
距离向匹配滤波完成脉冲压缩后的距离变化量为:
根据以上分析,假定雷达发射的雷达信号移频量为fd,那么干扰机发射的信号模型为:
信号经过雷达匹配滤波后会产生一个延时τ的假目标。
1.2.2 常规移频干扰验证
下面是通过MATLAB进行仿真验证的结果:
首先当雷达调频斜率不发生捷变时,设定如下参数。
真实目标在距离雷达2 000 m处,假目标与真实目标距离Δd=100 m(前移),带宽B=10 MHz,脉冲宽度Tp=50 μs,k=B/Tp,根据我们要移动的距离计算需要的移频量fd=1.33 MHz下面是进行常规移频时的效果图。
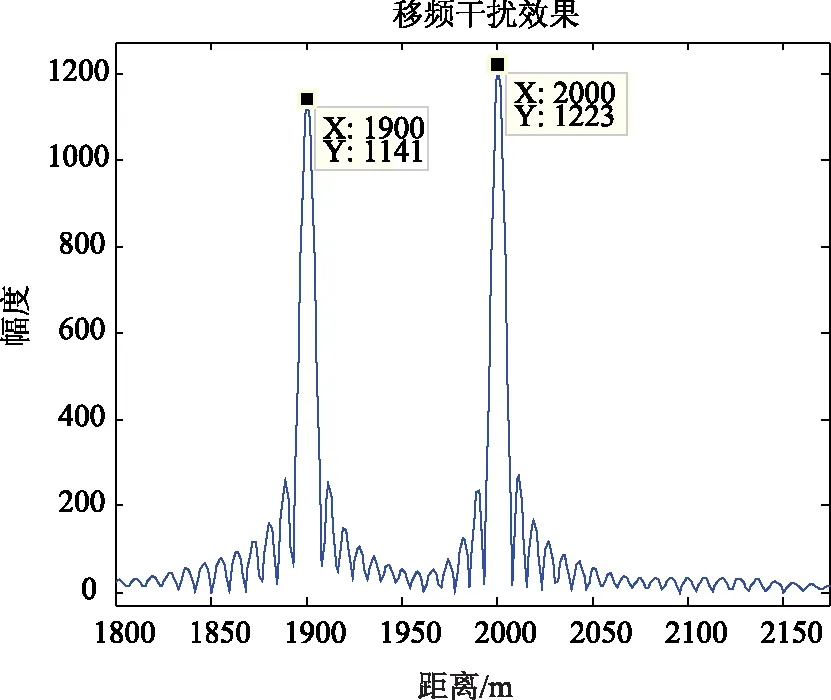
图1 常规移频干扰脉冲压缩结果
当调频斜率变为原来的三倍时,采用同样的移频量,得到的假目标位置如下图所示。
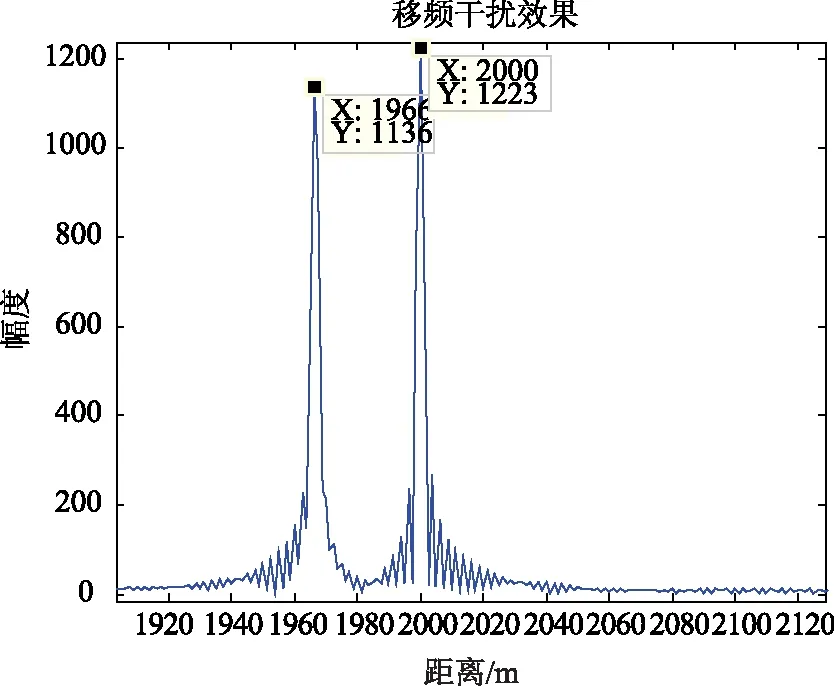
图2 雷达调频斜率捷变后常规移频干扰脉冲压缩结果
由以上两图可知,常规移频干扰可以产生前移假目标,由于干扰信号与雷达发射信号会有一定的失配,所以匹配滤波后假目标信号的幅度会略低于真实目标信号,而要获得距离固定的假目标,须实时获取雷达的调频斜率。
2 基于频谱扩展-压缩(SSC)的移频干扰
常规移频干扰首先是移频量依赖于对雷达调频斜率的侦测,可看出,要知道假目标距离差与移频量的一一对应关系,必须知道调频斜率。如果脉冲间调频斜率捷变,则固定移频干扰产生的假目标的距离也随之产生改变。在脉冲积累时,干扰产生的假峰由于不能在同一距离上获得积累而得到抑制。同样,在对付具有不同调频斜率的频率分集雷达时也会遇到同样的问题。这就是前面所述移频干扰方法在对付调频斜率捷变雷达时失效的原因。若要使得假目标信号可在同一距离上进行积累,必须使频移量随调频斜率的变化而变化,而实时获得调频斜率的准确测量值是不现实的,所以下面讨论一种无需获知雷达调频斜率即可获得距离稳定的假目标的理论基础即基于频谱扩展-压缩(SSC)的移频干扰理论基础。
2.1 SSC移频干扰基本原理
移频分为正向移频和负向移频,为分析方便,以下均以正向移频为例,线性调频信号重写为
则经过延时τ后,有
[j2π(f0t+μt2/2]exp(-j2πμτt)
[j2π(μτ2/2-f0t)]·exp[j2π(f0t+μt2/2]exp(-j2πμτt)
其中
上式两边同乘以s(t)s*(t-τ),有
s(t)2s*(t-τ)exp(-j2πμτt)exp[jφ(τ)]
整理得
(t-τ)exp[jφ(τ)]
由上式可见,等号左边即为常规移频干扰的数学表达式,只是取值范围略有不同,脉冲宽度减小τ,起始频率也变为f0+μτ,移频量为μτ,令等号右边为干扰信号sj(t),有
sj(t)=s(t)2s*(t-τ)exp[jφ(τ)]
由此得到移频干扰信号的另一种产生方式,SSC移频干扰产生方框图如下

所产生的移频干扰信号与常规移频干扰信号相比,最大的优点是干扰信号的产生并未求解调频斜率μ,避免了常规移频干扰对调频斜率参数检测的苛刻要求。由于Δf=μτ始终大于零,因此产生的假目标干扰总是超前于真实目标。与常规移频干扰信号相比,最大的优点是干扰信号的产生并未求解调频斜率μ,避免了常规移频干扰对调频斜率参数检测的苛刻要求。从上式也可以看出,干扰信号脉冲开始的一小段被截去,长度为τ,因此干扰脉冲宽度变为τ′-τ,如下图(a)所示。
若要产生负移频,即产生拖后的假目标。下面推导表达式。公式两边平方得
(-j2π2μτt)exp[j2φ(τ)]
两边同乘以s*(t),且将exp[j2φ(τ)]移到方程的左边,得
s(t)exp(-j2π2μτt)
可见,通过延时τ可获得2倍移频量μτ。
2.2 SSC移频干扰信号的匹配滤波器输出
这种脉冲宽度的变化使得干扰信号在匹配滤波后的输出具有了新的特性,不能直接套用常规移频干扰的结论,下面分析干扰信号在匹配滤波后的输出。
匹配滤波器冲击相应函数重写如下
h(t)=s*(-t)
则匹配滤波器输出为
so(t)=sj(t)·h(t)
当正移频时,因为Δf=μτ,代入上式得:
(t)*h(t)
可见,由于脉冲宽度被截短,SSC产生的移频干扰信号经过雷达匹配滤波器后的表达式不同于常规移频干扰的两段函数,而是变成三段函数。
在(-τ′+τ,0]范围内输出幅度衰减变为(1+(t-τ)/τ′),主瓣同时展宽,且输出频率也增加了一项-μτ/2,有一附加相位Δfτ/2。
第二段,即(0,τ]范围内,输出包络为一常数,为t-τ/τ′,不随时间的移动而产生变化,主瓣宽度也为一常数1-τ/τ′,输出频率为一线性调频信号。
第三段定义在(τ,τ′)范围内,表达式与常规移频干扰的表达式相同,具有相同的性质。
可以看到,由于是正移频干扰,因此峰值在第一区间,输出中没有固定频率,可以避免被识别,方法可以是使用SSC干扰,也可以在常规移频干扰的前面人为减少一个τ,达到去除干扰特征的目的。
为达到隐藏特征的目的,也可以对雷达信号进行时域截断处理,这样做虽然会损失一部分功率,但可以切实隐藏中心频点偏移的特征。但相比SSC移频干扰,时域截断移频干扰为了产生距离稳定的干扰目标,并且才可以讲中心频点准确搬移回原来位置,需要知道信号的调频斜率,然后实时获得雷达信号的调频斜率,这在现代战争复杂的电磁环境中是非常难的。
综合以上所描述的内容,SSC移频干扰具有很明显的优点,主要是:
a)无需调频斜率先验知识;
b)可以产生距离稳定的假目标,不易被雷达想干积累处理掉;
c)可隐藏移频干扰中心频点偏移的特征。
2.3 SSC移频干扰的物理解释
当信号表示成复数形式时,平方即倍频,因此对LFM信号进行平方运算,调频斜率增大一倍,而脉冲宽度没变,则带宽扩展一倍,当另一路经过延迟τ的信号到来时,取复共轭后两者相乘,则相当于把调频斜率又变回原来的值,得到移频干扰,移频量为μτ。
直观上,就是先将接收到的雷达信号调频斜率变大,经过一个很短的时间τ就可以达到很高的瞬时频率,当达到需要的瞬时频率时,再将调频斜率变为原来的初始值,得到移频干扰信号,干扰信号此的时瞬时频率比雷达回波瞬时频率增加一个μτ,当延迟τ不变的情况下,移频量Δf随着调频斜率的变化而变化,延迟τ不变,则假目标和真实目标的距离差就不变,避免了移频干扰受调频斜率先验知识的影响。
2.4 SSC移频干扰验证

经过仔细的观察,可以看出,干扰的波形相对于回波的形状有明显的变化,并且左右都变窄了,具体变窄的宽度应该是tau′=1.33×10-7s,接下来我们分析频域:为方便观察,右图为叠加对比后放大的效果图。
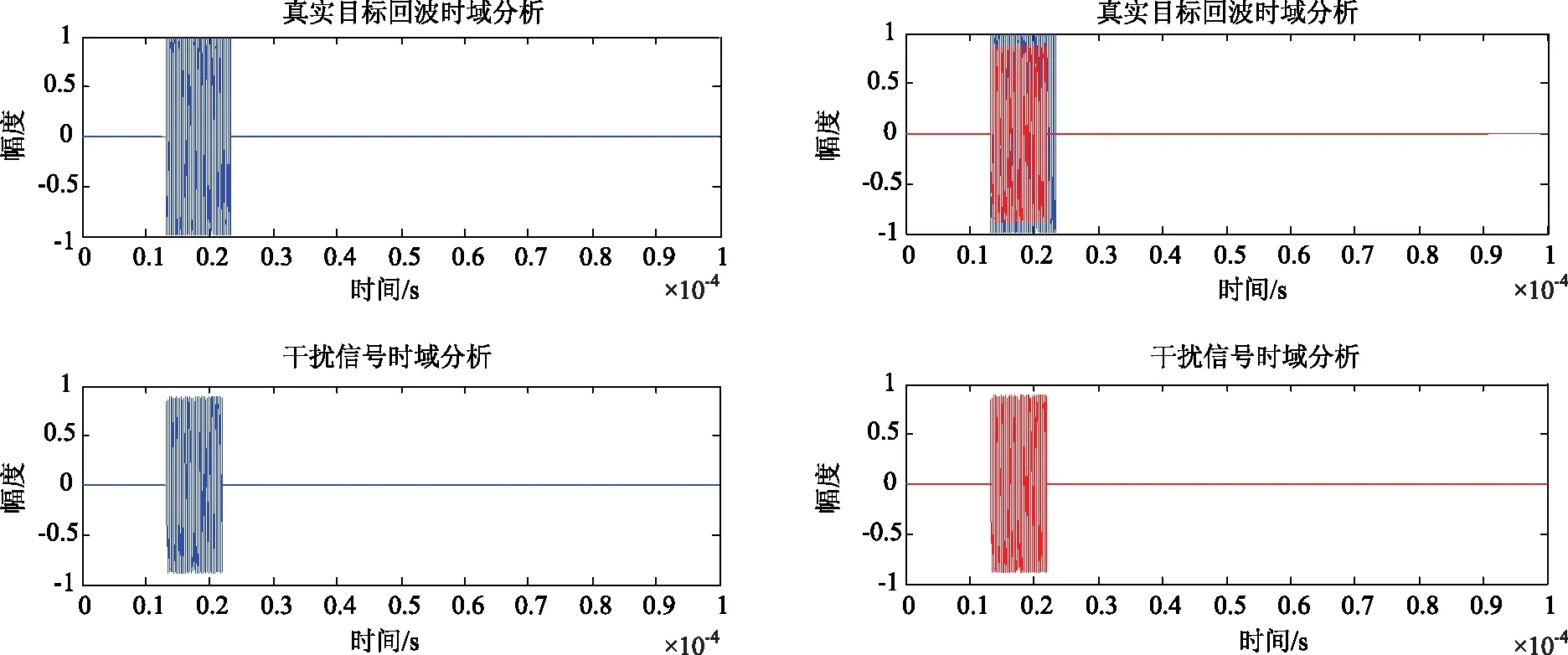
图3 SSC移频干扰信号频域分析
从频谱图来看,可以看出,频谱整个向右搬移了,移频量为Δf=1.33 MHz,接下来看匹配滤波后的频域波形,为方便观察,右图为叠加对比后放大的效果图。
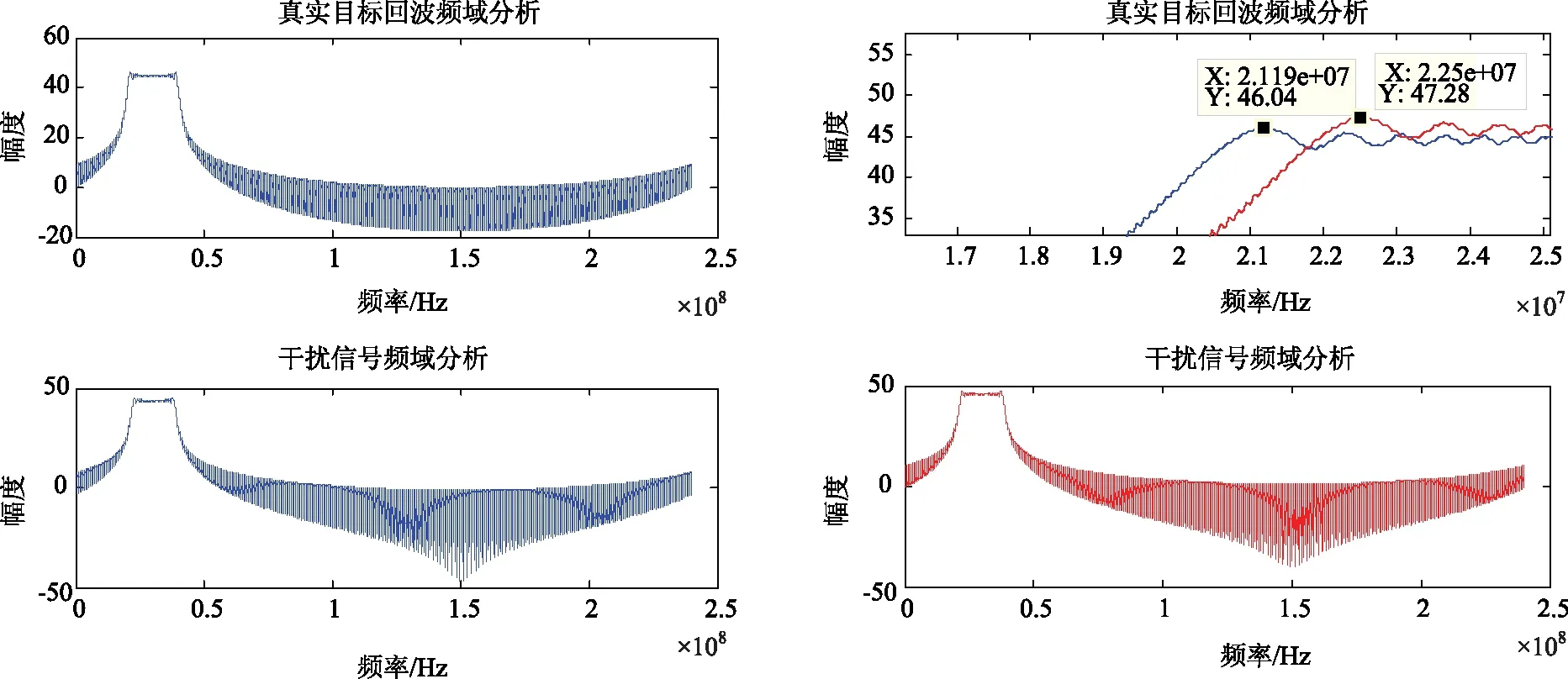
图4 SSC移频干扰信号频域分析

图5 SSC移频干扰信号脉冲压缩处理后的频域分析

为了验证SSC移频干扰对调频斜率捷变的雷达可以起到有效干扰,使雷达调频斜率变为原来的3倍时,假目标位置如下图所示,没有发生移动。
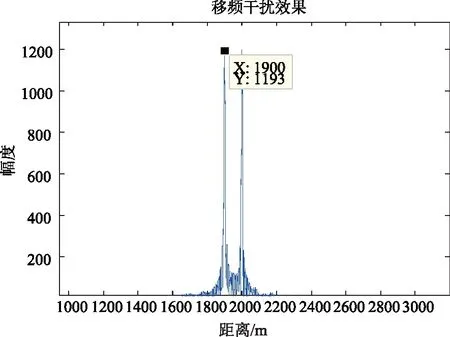
图6 SSC移频干扰效果
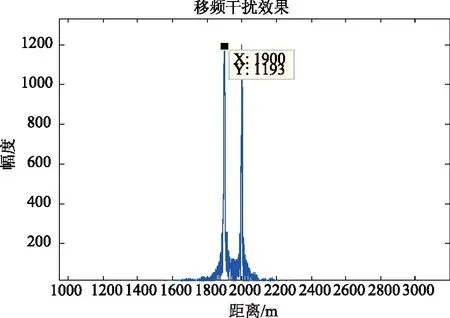
图7 雷达调频斜率捷变时SSC移频干扰效果
3 结 语
基于频谱扩展-压缩(SSC)的移频干扰不需要提前获取雷达的调频斜率信息,可以产生距离稳定的假目标干扰,在雷达相干积累处理中可以获得增益,不会被消除,从而弥补了常规移频干扰面对调频斜率捷变雷达时,不能产生有效欺骗干扰的缺点。
[1] 王玉军.线性调频雷达干扰新技术及数字干扰合成研究[D].西安电子科技大学.
[2] 王雪松.现代雷达电子战系统建模与仿真[M].电子工业出版社。
[3] Mark A.Richards.雷达信号处理基础[M].电子工业出版社.
[4] 金珊珊,王春阳,冯存前,田波.灵巧干扰及其对抗技术的研究现状与展望[M].舰船电子对抗
[5] 吴曼青.数字阵列雷达及其进展[J].中国电子科学研究院学报

徐志朝(1992—),男,硕士,主要研究方向为电子与通信工程;
E-mail:576295397@qq.com
姜 淼(1994—),山东人,硕士研究生,主要研究方向为信号与信息处理;
张培瑶(1992—),河南人,硕士研究生,主要研究方向为信号与信息处理;
曾大治(1977—),贵州人,副研究员,主要研究方向为系统仿真与实验验证技术;
刘 伟(1976—),北京人,工程师,主要研究方向为数字通信。
The Analysis of the Frequency Shift Jamming Based on Spectrum Extension-Compression (SSC)
XU Zhi-zhao, ZHANG Pei-yao,JIANG Miao, LIU Wei, ZENG Da-zhi
(Beijing Institute of Technology, Beijing 100000)
Deception jamming makes the radar get false information and lost the real target information by simulating radar target signal characteristic for the purpose of deception.As a way of producing deception jamming, frequency-shift interference can make up for the deficiency that delay forwarding interference cannot produce stable forward false target when facing the lowest frequency radar and the new system radar, such as the step frequency radar.Conventional frequency shift jamming must understand the prior knowledge about the slope of frequency modulation of the jammed radar and make it not produce ideal deception jamming effect when facing the frequency modulation slope agility radar.This paper mainly expounds a new way of frequency shift and uses MATLAB to analyze its interference principle and effect.
Shift frequency interference; Spectrum extension-compression; the frequency modulation slope prior knowledge.
2016-08-05
2016-09-20
:A
1673-5692(2016)05-463-07

