着眼知识结构 实施整体教学——和差积商变化规律的教学实践研究

郑东洪 方晨霞

一、问题来自学生学习的认识

人教版四年级上册数学教材安排了“积的变化规律”和“商不变的性质”的学习。积的变化规律对简便计算及后续解决小数乘法计算等起着重要的作用；商不变的性质主要是进行简便和小数除法计算以及对分数、比等内容后续知识产生正迁移。在四则运算中，不仅有乘除，还有加减，加减中有和差变化规律。

和差变化规律在小学数学的教材上并没有作为一个教学内容来呈现，但其的确有它的价值。那么孩子究竟对这部分知识掌握得怎么样呢？在学习积商变化规律之前，笔者对孩子进行了有关和差变化规律的前测。结果见图1。

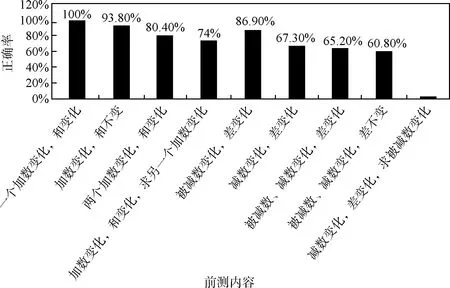
图1 前测结果分析

通过图1的前测结果来分析：孩子们对和的变化规律还是有一定的基础的，即使不上这一内容，孩子大多数也是有感觉的。差的变化规律虽然也有一定的基础，但是容易混淆，减数变化和差变化规律错误率高，说明孩子对减数和差反着变化不清楚。另外从前测数据可以看出，孩子对一种量的变化引发的结果变化还是掌握得比较好的，除了减数和差的变化关系，但两种量同时变化，从前测看，正确率还是比较低的。

我们的思考是：既然在孩子的学习路上需要这部分知识，而且孩子对这部分知识又不清楚，我们就不能忽视它。和差积商都有变化规律，从知识的产生、发展的角度来看，变化规律之间既有联系也有区别，我们可以尝试把和差积商变化规律作为一个知识整体，通过学习主题的重组集中进行教学。

二、改变源于知识结构化的思考

运算中的变与不变规律，教材是蜻蜓点水式的，给我们老师和学生的感觉是轻描淡写。那么学生学习真的是那么容易吗？这些规律又是独立存在的吗？它们之间有哪些内在的联系，教学中能实现关联并融会贯通吗？我们进行了深度的研究。

(一)学生学习的困难

教材上安排的积商变化规律的学习，是四年级上册的一个教学难点，之所以觉得这部分知识难，是因为变化规律多，孩子容易搞混淆。每一种运算都有自己的变化规律，以商的变化为例，就有以下几种：①被除数乘或除以一个数，商变了；②除数乘或除以一个数，商变了；③被除数和除数同时乘或除以一个相同的数，商不变；④被除数和除数同时乘或除以一个相同的数，商变了；⑤被除数乘或除以一个数，除数除以乘一个数，商变化。

孩子们不但要知道已知被除数变化、除数变化，商变化情况，还要知道商变化，被除数、除数变化情况。一个商变化就有如此多的类型，若四种运算规律合在一起，四年级的孩子抽象思维能力有限，极易搞混淆。同时学习四种变化规律，要求孩子都掌握并能正确应用，这对孩子来说也是个挑战。

(二)教学内容本质的再认识

积商的变化规律在教学上是一个难点。因为规律比较多，又有很大的相似性，学生容易混淆，以至于在作业时错误百出。根据对商变化类型的分析，学生需要掌握的变化规律很多，但细细思考，我们发现商的变化的根本是被除数乘或除以一个数，商发生了变化，除数乘或除以一个数，商变化。而商不变的本质还是因为被除数变，商跟着变，除数变，商反着变，最终商的变化抵消了。被除数和除数同时变化，而商变化是因为最终商的变化没有抵消。

将这些变化规律重新归类整理，我们认为商的变化规律孩子需要掌握的是：①被除数除以几，商随着除以几；②除数除以几，商反而乘几；③被除数除以几，除数也除以几，商不变或商变了。

其他的变化规律也是如此：

从和差积商的变化规律分析来看，变化规律可以分为两类：一类是变的规律，另一类是不变规律。而变与不变的规律中，和与积的变化规律相似，差与商的变化规律相似。但不论是变还是不变规律，其本质都是变化所引起的。所有的变化规律都是由一种量变化引发结果变化，两种量变化时结果可能变也可能不变，所以不论哪种规律，首先要让学生理解和差积商都是因为某个数怎么变而发生了变化。

(三)教学内容的整体性重构

通过对和差积商变化规律的本质思考，我们发现和差积商变化规律是有联系的，用一定的方式让孩子有联系地学习，能够让孩子更清晰地认识知识的本源，有意义的联系学习是学习数学的一种非常有效的方式，我们觉得这一部分内容可以作为一个有机整体，集中进行学习，便于学生对知识的沟通联系，辨别比较。所以我们打算在上三位数乘两位数这单元之前，对这四种变化规律内容用一定的方式恰当地组织起来集中学习，有利于孩子理解和迁移的知识结构，使学习内容不再简单孤立而碎片化。根据我们对这部分知识内容的思考，设计了表1所示的教学内容。

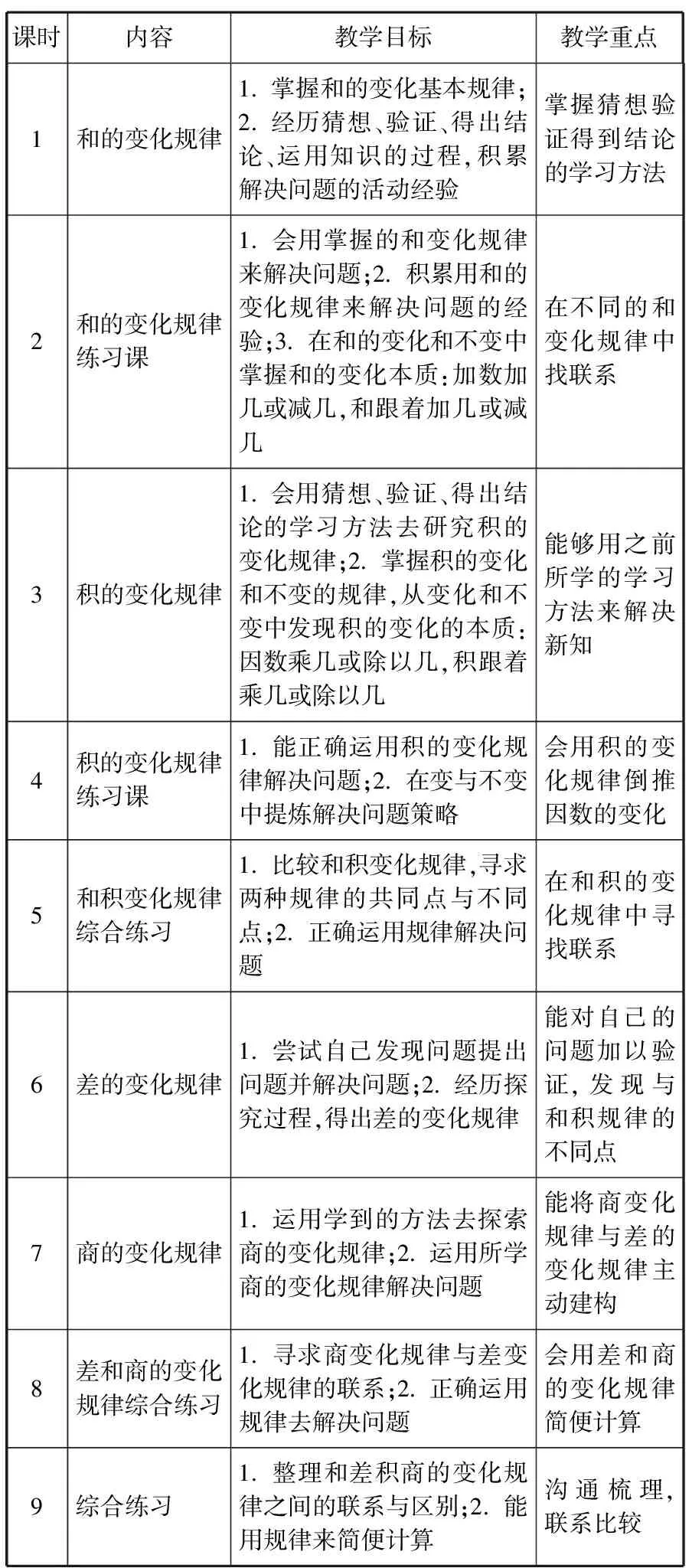
表1 教学内容安排表

三、重心在于主题式课堂实践

当我们有了前面这样的思考与分析，究竟这样的思考有价值吗？需要用实践去验证。于是，我们开展扎实的主题式课堂教学实践。

(一)重组知识，明确目标

和差积商变化规律的教学内容属于并列式内容，四种变化规律都有相似的教学目标，每一种变化规律要求孩子掌握的知识点也大致相似。

以和的变化规律为例，需要孩子掌握的内容如下：

知识方面：(1)一个加数增加几(或减几)，另一个加数不变，和也跟着加几或减几；(2)一个加数加几，另一个加数减相同的数，和不变；(3)一个加数加几，另一个加数减几(或加几)，和在变化；(4)已知一个加数加几，和减几，另一个加数怎么变；(5)能用和的变化规律解决实际问题：简便计算，错中求解等。

能力方面：经历猜想、验证、发现规律、运用规律的过程，提高发现问题、解决问题的能力。

(二)重构教学，由浅入深

我们把和差积商变化规律放在一起教学。从和的变化规律入手，孩子有基础，也容易理解和掌握。积的变化规律与和的变化规律类似，学生掌握容易一些，上完和的变化规律，接着上积的变化规律。差的变化规律有变化，放到积的变化规律之后，最后是商的变化规律。

从和差积商的变化本质来看，对每一种规律，我们都先让孩子理解一种量变化引起的结果的变化。孩子只有深刻理解一种量变化引发的结果的变化，才会对两种量变化产生的结果变化有深入理解。所以每种变化规律的教学，内容都由浅入深，凸显教学内容本质的一致性，体现学生学习的层次性。

(三)学习方式，融会贯通

除了知识的掌握上有很高的相似性外，在学习方式上也是互通的，猜想规律—验证规律—发现规律—运用规律是这部分知识的共同学习方法。

先研究和的变化规律比研究积的变化规律的优势是：对知识点的掌握不需要花很多精力，可以集中精力让孩子掌握猜想—验证—发现规律(图2)的学习方法。孩子经历猜测由无从着手到有方向合理验证，由教师帮助到自主进行，发现规律由单一到全面，有效促进教学效率的提高以及孩子学习能力的发展。学生在不断利用这些概念通过正迁移解决新问题的过程中，数学核心素养得到发展。

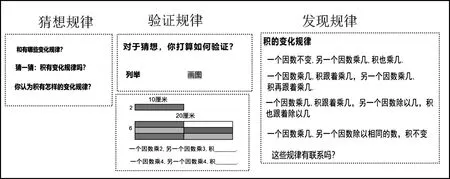
图2 教学过程图

(四)联系沟通，内合外联

如果每一个内容都是分散独立的教学，一定会给孩子增加记忆和理解的负担，有联系的学习则能提高学习效率。和与积的变化规律很相似，但也有区别。差、商的变化规律相似又有区别。

1.构建联系

我们在让孩子学习了和的变化规律之后，接着学习了积的变化规律，就是想让孩子主动建构和与积的变化规律之间的联系。

师：你认为积有怎样的变化规律呢？生：一个因数乘几，积也乘几。生：一个因数除以几，积也除以几。生：一个因数加几，积也加几。生：一个因数乘几，另一个因数除以几，积不变……

师：积是不是有这样的变化规律呢？你能验证这些猜想是否正确吗？以6×4为例进行研究。

孩子通过举例验证后，发现因数只有乘几除以几时，积才会乘几或除以几。

2.同中求异

在学习差的变化规律时，学生在猜测减数与差的变化规律时，一部分孩子会觉得减数怎么变，差也跟着怎么变，这是受和积变化规律的影响，通过验证和交流之后，发现减数与差的变化是相反的。除数和商也同样存在着相反的情况。而这一点正是孩子容易混淆的。

师：和差积商的变化规律中，哪些不变规律是一致的？生：和与积不变的规律是一致的，差和商的变化规律是类似的。生：我记住了和的变化规律，就记住了积的变化规律，我记住了差的变化规律，就记住了商的变化规律。

师：和积不变规律和差商不变规律之间有什么不同？生：和积中变化都是一致的，差和商中减数与差、除数与商是反着变的。

3.异中建同

虽然和差、积商是逆运算，它们之间有着相反的变化规律，但是，这些变化规律最终还是趋向一致的。

师：它们之间就没有联系吗？

生：和不变是因为两个加数变化，和的变化最终抵消了；减数变化差反着变，正因为反着变，差最终还是抵消了，所以最终的不变都是将和或者是差的变化最终抵消了。

只有在联系与对比中学习，学生才会对所学知识正确辨析，头脑中留下正确的知识。

(五)主攻疑难，凸显思维

在和差积商的变化规律这一知识体系的学习中，学生除了因规律多容易混淆之外，已知一种量的变化，结果的变化，逆向思考另一种量的变化，这是教学上的难点。如果只有一个不变量，那么逆向变化的难度并不大，难的是已知两种量在变化，倒推另一种量的变化。与此相对应的试题有：

(1)两数相加，一个加数减少12，要使和增加4，另一个加数应( )。

(2)两个数相乘，一个因数乘5，积除以2，另一个因数应( )。

(3)两个数相减，如果被减数增加32，要使差减少52，减数应( )。

(4)两个数相除，被除数乘16，要使商乘4，除数应( )。

逆向思维的题，对孩子来说是很难的，最难的是减法和除法。但对和差积商变化规律本质理解之后，学生能充分展现自己的思维。

以两个数相除，被除数乘16，要使商乘4，除数应( )为例。

复杂的题的变化是由基本的变化演变而来的，不论多复杂，都是对一种量变化而引发商的变化的运用。所以让孩子正确表达，展示自己的思维过程，既巩固了一般规律，也是正确解答复杂变化的必要措施。

(六)查漏补缺，及时练习

和差变化规律教材上没有，积商变化规律教学编写得很简单，配套练习很少，需要我们老师去设计一些练习，及时巩固课堂教学。根据我们的预设目标，这一部分知识，主要练习内容有两部分：(1)对变化规律的巩固；(2)增加了简便计算。根据教学内容，我们每节课后都设计相应的配套练习，通过不同形式的练习，及时了解孩子对知识的掌握情况，查漏补缺，发现孩子哪块知识掌握得不够好，就可以马上进行补救。

四、反思修正，且行且进

1.我们将和差积商变化规律放在一起教学，虽然增加了和差变化规律，但是在实践中用联系比较的学习主题式教学，方法上触类旁通，绝大多数孩子能够正确区分，掌握的规律不会混淆。

2.在教学中坚持让孩子理解一种量变化引发结果的变化是根本，是解决两种量变化结果变与不变的基础，也是解决逆向求其中一种量变化的基础。一切变化规律都是从一种量的变化开始。学生通过正迁移解决新的问题，数学核心素养不断得到发展。

3.要让变化规律解决问题成为孩子的思考习惯。和差变化规律很多时候在简便计算中发挥着重要的作用，当孩子看到题目要求用简便方法计算时，他会不自觉地想到运用这些变化规律，如果题目上没有要求简便计算，比如：在○里填上“>”“<”或“=”。

420×60○42×600

240×36○480×18

在这样的题目中，孩子能有意识地运用积不变规律去解决问题，这也是我们老师所希望的。路漫漫，我们将在已有实践基础上，不断探讨，找到更为有效的教学方法。