基于结构光和深度神经网络的3维面形重建

代金科,郑素

(1.西南石油大学 电气信息学院,成都 610500;2.西南石油大学 理学院,成都 610500)

引 言

在测量与恢复物体3维面形的领域,以传统结构光法为原理的3维测量有着重要意义,如位相测量轮廓术法(phase measurement profilometry,PMP)和傅里叶变换轮廓术法(Fourier transform profilometry,FTP)等等。这些经典方法对于3维面形的重建已经有了非常大的成效,PMP法能够进行针对于点的初相位求解,解决了被测对象面形的非均匀反射引起的偏差,测量的准确度为等效波长的1%～10%;FTP法只需获取单幅调制图就可以复刻出被测对象的3维面形,并且含有高速和高精度恢复的优点。但是PMP法对正弦光栅的稳定性和相移设备的精密性要求都较高,否则就会存在比较大的测量误差,其测量目标也只适合于小尺寸物体;而FTP法存在频谱混叠现象且缺乏迁移适用性,采用FTP法也有可能因为基准频和零频频谱掺杂导致无法进行准确的窗口式波过滤,从而无法正确恢复被测对象的面形结构。此类经典方法在解相位步骤时都会过于繁琐,亦或是噪声过大光源混杂,或在测量断崖式高度陡变物体等病态问题时,效果往往不尽如人意。

随着人工智能时代的到来,算法图像处理和神经网络于众多方面迅速兴起,其中非常多的算法和框架都被引入到了3维面形重建之中。MIN等人[1]利用最小二乘法测量3维物体面形粗糙度。GUO等人[2]以改进简化的反向传播(back propagation,BP)神经网络模型提高3维面形测量精度。本文作者通过对样本数据特征的采集和算法优化,训练一种深度神经网络模型来恢复物体的面形信息。

1 经典结构光法的面形恢复原理

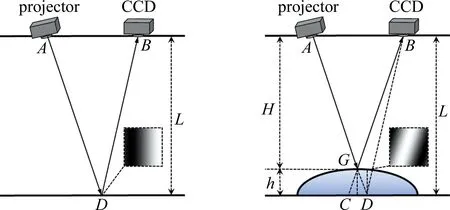
图1 结构光法面形恢复原理

通过相似三角形△ABG∽△CDG的几何关系,化简并最终得到物体表面一点(x,y)的高度h,计算过程如下：

(1)

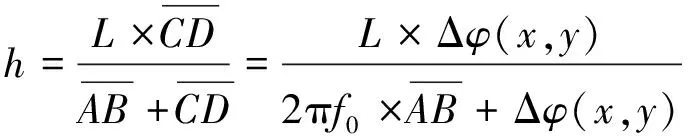
(2)

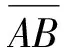
I(x,y)=R(x,y)·[A(x,y)+

B(x,y)·cosφ(x,y)]

(3)

(4)

式中,I(x,y)表示被测对象一点的光强值,R(x,y)表示被测对象表面非均匀反射系数,A(x,y)为背景光强度,B(x,y)为调制度,φ(x,y)为相位值,N为相移总步数,n为第1,2,3…步相移,In(x,y)为第n步相移时(x,y)点的光照强度。(3)式为CCD相机接收到的光强信息的表达式;分别设相移量为0,π/3,2π/3得到3个方程,并联立求解,可得相位表达式(4)式(过程略)。3步相移变化如图2所示,为一个相移方向上的条纹与调制条纹图。图中,φx,1表示投影条纹沿x方向上的第1步相移调制图,φx,2表示投影条纹沿x方向上的第2步相移调制图,φx,3表示投影条纹沿x方向上的第3步相移调制图。

图2 3步相移调制

不难看出,以PMP法还原高度信息,会在最后求取相位差时,包含一个反正切解相位的步骤,而通过相移法求得的相位值域会被限制在(-π,π)的区间上,故必须对其进行一个反正切运算,即解包裹处理,才能正确恢复出被折叠的真实高度信息,而此过程往往会使得计算过程变得冗杂而困难。所以,本文作者尝试以新的视角来思考这个问题,希望找到一个数学函数,来拟合物体的光强信息和此点高度值的直接关系。

2 深度神经网络的面形重建原理

2.1 深度神经网络的基本结构

深度神经网络(deep neural network,DNN)的结构如图3所示。网络框架由含32层中间隐藏层构成。层间激活函数为tanh,以σ表示,层间连接采用可有效防止模型过拟合的随机舍弃方式。每层隐含层含有18个记忆神经元,输入为单个像素点的9维光强特征,输出为此点的对应高度预测值。

图3 深度神经网络拓扑图

机器学习中的神经网络模型在本质上是一种标签学习算法[3],通过使用样本集训练学习模型f(·)：Rm→Ro,其中f(·)表示两集合间的映射逻辑关系,Rm和Ro分别表示有m和o个元素的集合。此种模型无需相机的标定和解包裹等繁杂过程,直接建立输入量和预测值之间的函数关系。Rm的下标m在神经网络模型中表示输入样本的特征维度数,Ro的下标o为模型预测值的维度数[3],即输入一条特征X=[x1x2…xm]T和标签y,神经网络通过学习训练,可以拟合出一个高纬非线性函数。在输入结点与输出结点之间,会存在一个层或者多层的非线性层,称为隐藏层。

图4是1维输出且只含有1层隐藏层的多层感知机[4](multilayer perceptron,MLP)。在此MLP结构中,样本特征由输入层导入,为一列代表样本特征值的神经元构成。信息传递途径隐藏层,上一层的信息经过下一层隐藏层中的结点进行加权求和：z=w1x1+w2x2+…+wmxn,其中参数wm为各输入项的加权值,加上一个偏置项后,由非线性单元进行z值的非线性转换。最右边的层叫做输出层,其收到的传递值是最后一个隐藏层经过非线性加权变换的输出值。而DNN的核心原理就是对MLP的横向方向进行隐藏层的层数拓展[5]。当网络结构确定后,神经网络的训练过程就是求解所有层间权重和偏置的过程,在整个神经网络模型训练完成后,即可对新的物体直接建立其光照强度和真实高度信息,如图5所示。

图4 多层感知器结构

图5 DNN 3维重建实现过程

DNN模型在本质上是一个处处可导的多元复合函数,在理论上能拟合出任意维度的超曲面,其训练过程是数据在网络中正向传播,再以反向传播求取函数梯度更新权重,以进行参数迭代求解目标函数最优解的过程。具体训练流程如图6所示。

图6 DNN训练流程图

2.2 DNN训练数据采集与预处理

通过改变条纹光的投影角度,增加了神经网络训练样本的特征维度。更多维度的光强信息训练,能使得模型鲁棒性增加[6],使得训练好的模型在投影系统参数(如环境光强噪声、测量深度等)强噪音的情况下能够精确复现出被测对象的3维面形。在条纹光的部署上,与传统N步相移法在单一方向上改变条纹光相位不同,将周期为T=8 pixel、变量区间为0～512 pixel的仿真余弦条纹以0°、45°和90°3个旋转角度,以15°倾斜角投影在被测物体上。由于被测对象的面形起伏,当正弦条纹光投影到被测对象上时,会让光栅条纹的相位发生调制型变化,再用CCD相机收集这些条纹光光强信息组,得到总共9幅条纹图,如图7所示。

图7 条纹投影调制模式

图7中,I0°,φ1,I0°,φ2,I0°,φ3为投影条纹光于0°旋转角下沿水平方向经3步相移调制后的调制条纹图。I45°,φ1,I45°,φ2,I45°,φ3为投影条纹光于45°旋转角下沿对角线方向经3步相移调制后的调制条纹图,以此类推。输入层以条纹调制前后总计9个光强信息作为训练集维度特征,分别记为F1～F9,输出值以每个点的真实高度值作为其自身标签,即y。投影仪本身不发生位置和角度改变,通过编码调整投影条纹的旋转角,可以得到同一点在不同条纹角度下的光强信息。单点光照强度的特征采集方式如图8所示。

图8 单点光照强度的样本采集

在图8的样本集表格中,y1～yi表示各样本点对应的真实高度值,即为样本标签。将每个样本数据写作计算机更易于处理的向量形式,以每个像素点在9幅调制图中所对应的光照强度值作为其特征值I1,1～I1,9。在训练时,若取训练集的一个像素点的特征值和标签值组成向量X1,作为神经网络的输入值,则其表达式为：

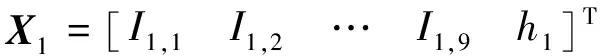
(5)

式中,X1表示此点是(1,1)位置的像素对应的样本点,I1,1～I1,9表示同一点在3种旋转角下3步相移的光强值,h1表示此点的真实高度值。对于一个分辨率为512×512的重建对象,一共具有512×512=262144个像素级样本,记为训练集S={X1,X2,…,X262144},以训练深度神经网络的拟合函数。

2.3 DNN的前向传播与代价函数

图9为简化的节点信息传递图。红色表示权重为负,蓝色连线表示权重为正,灰色连线表示随机舍弃[7]的层节点;方框中的绿色曲线表示激活函;a0,1表示神经网络输入层的第1个输入项,ω1,1表示a0,1项在第1层神经网络的第1个权重系数,b1,1表示第1层神经网络的第1个偏置系数,以此类推。经过激活函数将线性映射转换为非线性关系,得到神经网络第1层的其中一个输出a1,1,以tanh函数为线性转非线性的映射激活,其转换关系如下：

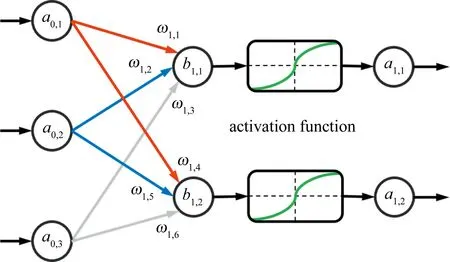
图9 简化的节点信息传递图

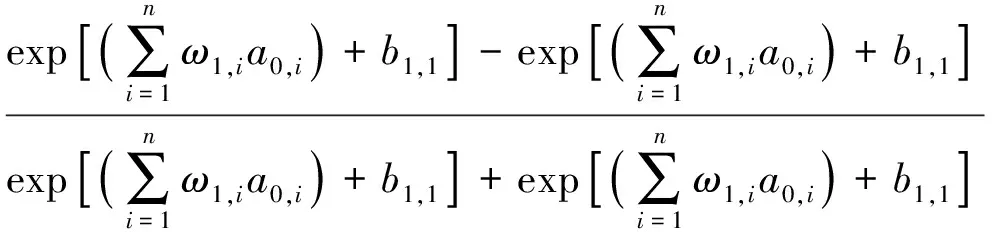
(6)

BP神经网络是一种采用梯度下降算法[8]进行学习的多层信息前向传递误差反向传播神经网络,根据深度信念网络[9]理论,BP神经网络隐层的神经结点数越多,就越可以以极大精度拟合任意连续超曲面。BP网络有特征光强值的前馈传导和逆向传播两个相互影响制约的步骤[10]。特征光强值的前馈传导步骤是：输入的特征光强值通过输入结点和随机舍弃的隐藏层逐一计算出各单元输出值。逆向传播步骤是：递归循环地计算模型预测值与样本标签高度值的残差,并根据代价函数最小化来自动调整每个神经元结点的权重比例和后续激活阈值[11],最后以全连接作为输出预测值[12]。将神经网络中的权重和偏置参数以和的形式记录,其中下标i和下标j分别表示此参数是属于第i层网络的j个权重或偏置参数。输入量A1为样本数据X1除去标签值h1的剩下部分,输入量A1的各分量在神经网络中传播时以an,m表示,其中n表示数值此刻正传递于神经网络的第n层,m表示此分量为A1的第m个特征数值。记神经网络第1层所有权重参数组成的系数矩阵为W1,所有偏置系数组成的偏置向量为B1,则神经网络第1层的层间线性矩阵映射关系如下：

W1A1+B1=

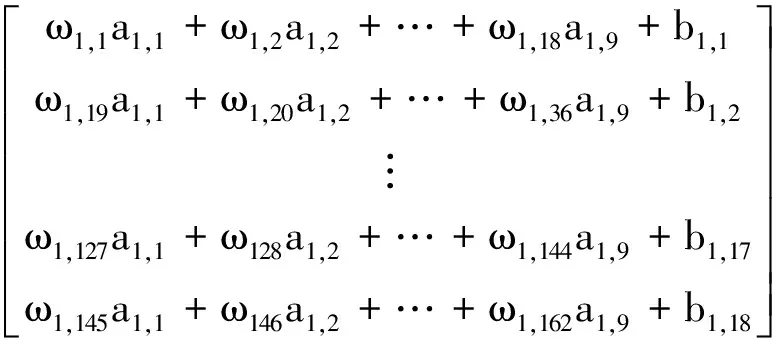
(7)

将上述结果记为Z1,再通过激活函数tanh对Z1的第1个分量z1,1为例,对于层间非线性软化的转换,可将(7)式简化,记Z1=W1A1+B1,其转换关系如下：

(8)

B2]…+B31}+b32,1〉

(9)

(10)

本文中以弹性网络[12]作为目标函数惩罚项,同时使用l1和l2范数进行正则化,将二者的优点都结合了起来,兼顾了拉索回归[13]和岭回归[14]的各自优势,其目标函数惩罚项Ω(W)的数学表达式如下：

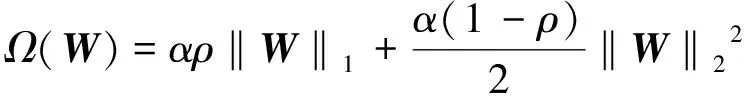
(11)

(12)

问题转化为求取目标函数最小值时对应的参数值,一旦将所有权重系数和偏置系数,神经网络模型就确定了。现在转化为如下数学问题：

(W,B)=arg minfobj

(13)

2.4 随机梯度下降迭代过程

本文作者使用非常适合处理万量级以上样本数的随机梯度下降[16](stochastic gradient descent,SGD)的迭代算法来求解上述问题,如本训练对象的512×512=262144个像素级样本。因SGD是针对每个样本进行逐一迭代的[17],所以SGD对样本集的特征缩放非常敏感,需要将样本特征即9维的光照强度信息,全部归一化到均值为0、方差为1的区间内。每次将样本集S={X1,X2,…,X262144}中的多个样本传入算法流程,以迭代方式更新参数值,其迭代公式如下：

(14)

2.5 反向传播求取梯度

神经网络的反向传播,是一种以链式法则求取函数梯度分量的过程[19]。通过增加电脑内存占用为代价,提高神经网络的训练速度。目标函数的梯度为：

(15)

式中,梯度的分量为目标函数的偏导数, 由于神经网络的层层复合,参数所在神经网络的层级越初级,其偏导计算式越繁琐：

(16)

反向传播即以占用更多内存为代价,如图10所示。算力较强的计算机,在DNN架构的设计策略上,可增加网络的宽度和深度[20],或使用不同的处理器,如在图形处理器上进行并行运算。在提高拟合精度的同时,还能显著减少神经网络的训练时间[21]。

图10 计算机内存使用示意

将各个链式中间项写入计算机内存,便可快速求解任意第p层的第q个权重的偏导数,让神经网络可以较为快速地迭代出收敛区间下的神经网络全参数。只要训练完成,迁移适用性也会变得非常强,这使得在测量新型面形时,无需再重复训练,而神经网络权值参数的优化更新,是一个可多次输入样本簇并迭代优化的过程。

2.6 多次训练至网络收敛

为了增加网络的泛化能力,本文作者使用了总计260×104个像素级样本点对神经网络进行参数训练,且对每类物体进行多个轮次训练,体现了神经网络的进阶学习性。如加入刀锋和波纹状样本进行训练,可强化神经网络对物体表面划痕或刮痕的重建鲁棒性,如图11a和图11b所示。加入随机噪点样本进行训练,可强化神经网络对表面含较多毛刺物体的重建鲁棒性,如图11c所示。

图11 不同类型的仿真训练物体

将两个呈共轭关系等阶梯状物体的像素点记为样本集送入神经网络再次迭代参数,既可优化神经网络在断崖式物体面形测量上表现,同时又优化了此类阶梯型样本数据在空间上分布不均衡所导致神经网络的欠鲁棒性,如图12和图13所示。

图13 倒置共轭阶梯

总共进行193个 轮次时均方误差(mean square error,MSE)达到一个收敛区间(1.0×10-8～1.0×10-9)。图14为深度神经网络模型输出高度值的MSE随迭代轮次的变化结果。图15为其它性能指标的参数走势图。当然,如此高的测量精度只是在理想样本集上精度的表现。在对实际物体进行测量时精度会降低1～2个数量级。作者将收敛的DNN模型储存起来,然后在真实物体数据集上进行面形重建实验。

图14 MSE收敛过程

图15 其它参数变化

因本文中重建物体面形的方法与其自身实验装置的耦合性较强,部分主要实验装置配置和神经网络的最优参数如表1所示。

表1 本文中的DNN训练参数与实验配置

3 深度神经网络的面形重建实验

本文作者使用相关软件进行仿真重建实验,以训练好的深度神经网络重建了软件中内置山峰函数的绝对值函数,还原结果和误差分布图如图16和图17所示。

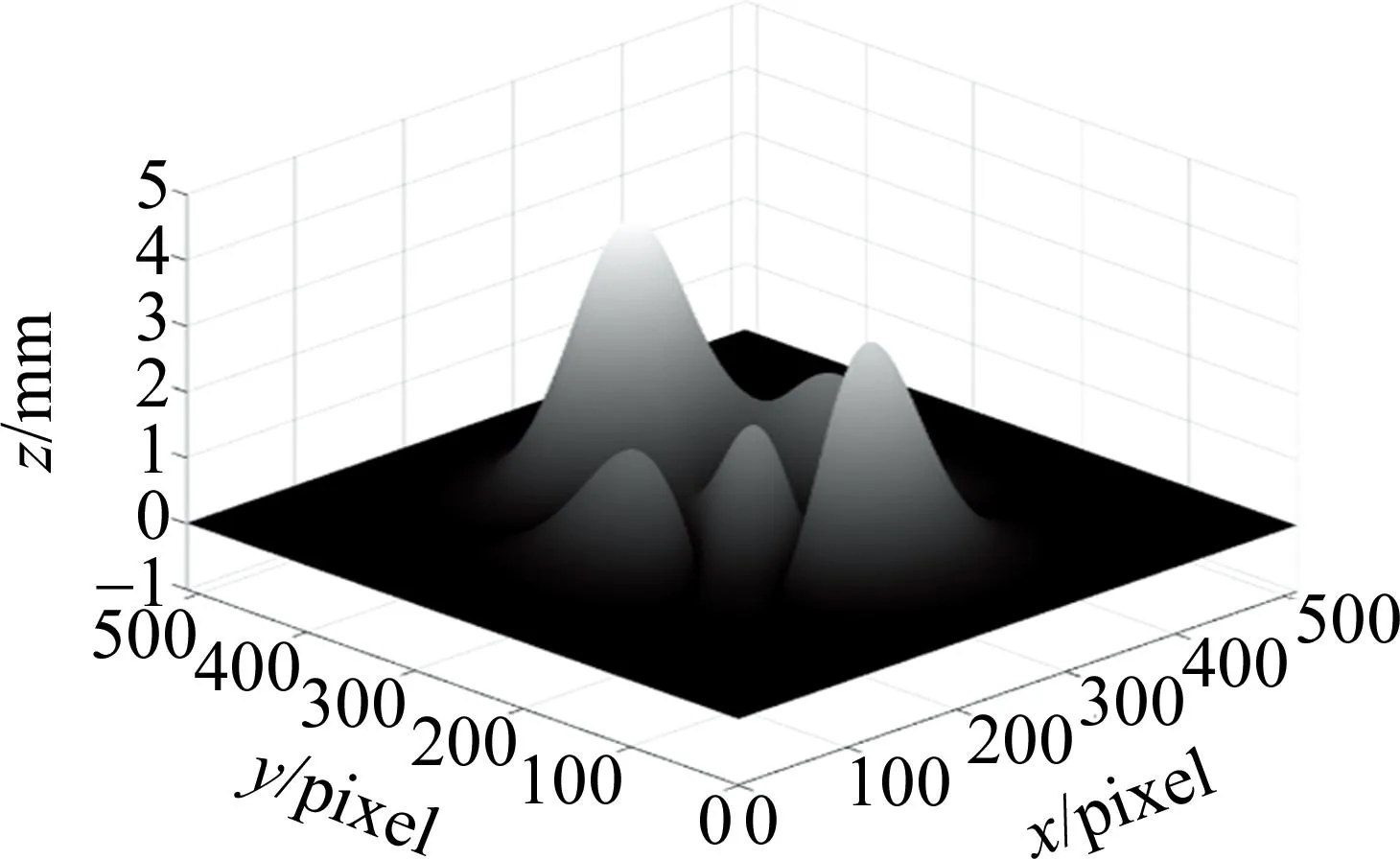
图16 山峰绝对值函数重建

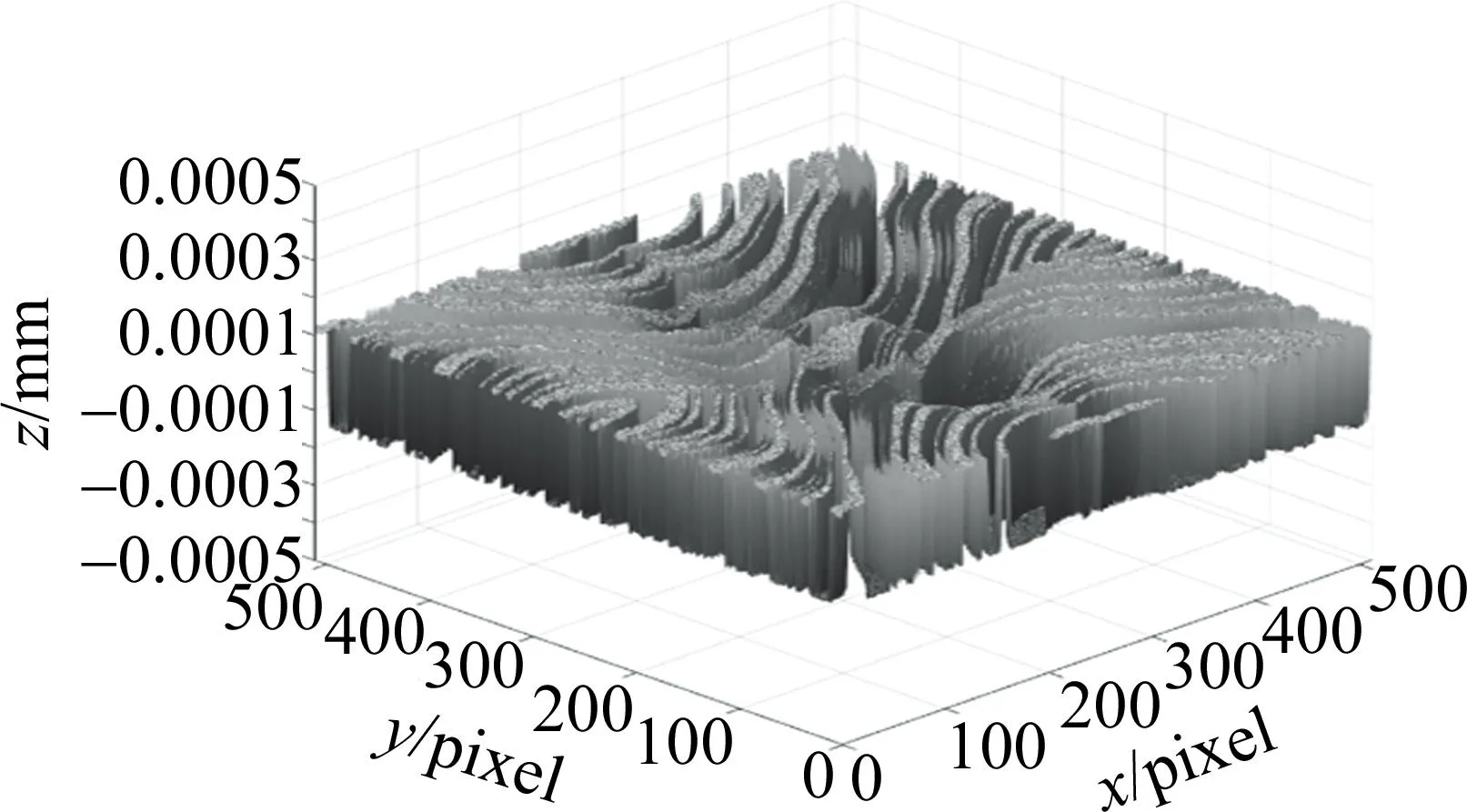
图17 重建误差分布

经典FTP法和PMP法的重建单点最大误差大于1.00 mm,MLP法的重建单点最大误差为1.00×10-2mm。GUO等人[2]的BP神经网络的平均重建时间为3.8 s,单点最大误差为0.34×10-3mm。本文中的DNN单点最大误差在1.42×10-4mm以下,重建时间达到了非常短的0.27 s之内。因为整个DNN的高度复原计算方法是对单点进行的直接映射关系预测,结构相对简单,也没有较大的区域性误差。本文中的DNN对于物体面形的重建从速度和精度上相较于其它方法都存在着优势,且对于反光材质的物品(如铁制镀漆物品)的还原结果也较为优良。

考虑到不同测量距离和测量环境对面形恢复精度的影响,对西南石油大学铁制校徽进行了对照重建实验,如图18所示。对本文中方法的面形重建能力进行了定量评价,具体数值如表2所示。

表2 不同条件下重建能力对比

图18 铁质校徽对照重建实验

本文中的DNN具有一定的迁移泛化能力,即一旦网络参数全部训练完毕,便可在无需再次训练情况下迅速重建物体面形信息。即使在光线干扰较强的室外,且测量距离小于10 m之内的情况下,对物体的重建平均误差不超过9.96×10-4mm。

为了验证本文中DNN在真实情况下的对物体面形恢复的效果,作者对太阳神鸟(仿品)和某观音饰品进行了真实试验,如图19和图20所示。

图19 太阳神鸟仿品重建

图20 观音饰品重建

同时,为了对比本文中DNN对物体面形恢复效能,作者以同等阶梯状物体的面形恢复效果作了横向对比。其中,样本规模是指参与训练的总样本数量,样本规模和训练轮数越大,在相同性能的计算机下耗费的计算资源和计算时间也就越大。对比结果如表3所示。

表3 不同方法重建阶梯状物体性能对照

4 结 论

本文中采用了以较多维度的相关参量作训练集来表征物体面形高度,即GUO等人[2]提出的进一步优化的方法之一。根据深度信念网络理念,只要模型训练的批次取得合适范围,训练后期步长足够小,并且整个模型有更多的神经结点和隐藏层层数,拟合任意连续超曲面都是可行的,甚至可以让损失无限趋近于0。特征维度增加之后,需要更高质量的样本集来训练神经网络,需要更精准的仪器和低噪声的光照环境中所收集的样本集来进一步提高面形恢复精确度。作者将相位测量轮廓术中的相移思想运用到神经网模型的样本集收集中,通过不同角度的条纹增加了单点光强信息的特征数,同时防止了神经网模型欠拟合。本文中的方法省去了传统相位测量轮廓术和傅里叶变换轮廓术的繁琐计算过程,优化了神经网络模型的训练样本采集方式,在实践中可降低计算时间和设备成本,为实时面形复原提供了一定的可行性。