基于Mach-Zehnder干涉仪的自相似激光器压缩系统设计

庞亮雨,张巧芬,高梓皓,陈楚浜,吴铭扬

(1.广东工业大学 机电工程学院,广州 510006; 2.广东工业大学 精密微电子制造技术重点实验室,广州 510006)

引 言

高功率超短脉冲[1]由于超强特性和较高的峰值功率而被广泛应用,如光时分复用通信[2]、金属玻璃激光切割[3]、纳米连接[4]等等。高功率超短脉冲可以通过价格昂贵的锁模激光器[5-8]直接产生,或者通过脉冲压缩技术[9-13]获得。大多数的锁模激光器[14]产生的脉冲脉宽低至几皮秒,再通过脉冲压缩方法来获得飞秒脉冲。在最近的研究中,不少学者通过级联单模光纤来获取峰值功率较高的超短脉冲,虽然能够获得峰值功率高的超短脉冲,但是脉冲基座较大[15-16]。马赫-曾德尔干涉仪(Mach-Zehnder interferometer,MZI)[17]作为脉冲压缩方法之一,其优点是在获取脉宽较窄的脉冲同时能够减小基座脉冲能量。自相似脉冲[18-21]能够在传输过程中保持波形不分裂且啁啾严格线性,非常有利于通过脉冲压缩技术来获得高功率的超短脉冲。基于此,本文作者研究设计了一种基于级联单模光纤的MZI的自相似锁模激光器脉冲压缩系统。

本文中将中心波长为1550 nm的高斯脉冲输入自相似锁模激光器中,主要研究了自相似脉冲的演化情况以及自相似脉冲在MZI的压缩特性。本文作者将具有不同2阶色散的单模光纤级联起来,分析了脉冲的峰值功率、半峰全宽等参数,优化设计了干涉仪上下臂的单模光纤的最佳长度,最后分析了3阶色散对于脉冲压缩的影响。

1 自相似脉冲产生及MZI的理论分析

自相似脉冲可由光纤激光器、色散渐减光纤或非线性渐增光纤产生,本文中采用掺铒锁模激光器来实现自相似脉冲的演化。分别构建激光器和MZI的数值分析模型,便于分析脉冲在演化和压缩时的传输特性。

1.1 自相似锁模激光器数值分析模型

自相似锁模激光器能够将任何类型的输入脉冲演化成自相似锁模脉冲。这种激光器由抽运光源、掺铒增益光纤(erbium-doped gain fiber,EDF)、滤波器、波分复用耦合器(wave division multiplexing coupler,WDM)、可饱和吸收体(saturable absorber,SA)、耦合器(output coupler,OC)、色散补偿光纤(dispersion compensation fiber,DCF)及单模光纤(single-mode fiber,SMF)组成,如图1所示。

增益光纤采用掺铒光纤,脉冲在增益光纤中的传输方程表示为[22]：

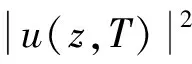
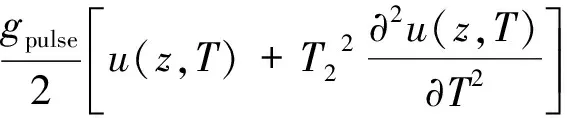
(1)

式中,z为光脉冲在光纤中的传播距离,u(z,T)为脉冲包络的慢变幅值,时间量度T在一参照系中随脉冲以群速度vg(T=t-z/vg)运动而测量,t为时间,βEDF,2为增益光纤的2阶色散,βEDF,2=23 ps2/km,γEDF为增益光纤的非线性系数,γEDF=4.7 W-1·km-1,gpulse为增益总量,gpulse=g0/(1+Epulse/Esat),小信号增益系数g0=30.4 /m,Epulse为光脉冲的能量,Esat为增益饱和能量,Esat=60 pJ,增益带宽时间T2=λ2/(2πcΔλ),λ为输入脉冲的波长,c为光速,Δλ为增益带宽。

耦合器将一部分的脉冲输出,输出的比例为10%。

可饱和吸收体透射率表示为：

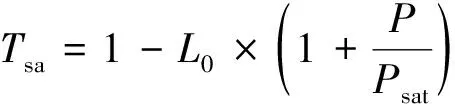
(2)

式中,P为脉冲的瞬时功率,Psat是可饱和吸收体的饱和功率,Psat=1500 W,L0为调制深度,L0=0.73。

色散补偿光纤起改变腔内净色散的作用,可用非线性薛定谔方程表示[23]：

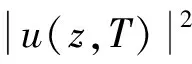
(3)

式中,βDCF,2、γDCF分别为色散补偿光纤对应的2阶色散系数和非线性系数,βDCF,2=-130 ps2/km,γDCF=1.3 W-1·km-1。

脉冲在SMF中的演化不考虑光纤的损耗和高阶色散,采用非线性薛定谔方程来表示：

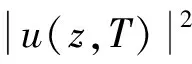
(4)

式中,β2为单模光纤的2阶色散系数,γ为单模光纤的非线性系数。对公式进行分步傅里叶法来研究激光器输出脉冲在SMF中传输特性。

将(4)式改写成如下形式：

(5)

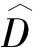
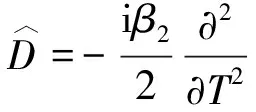
(6)

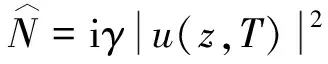
(7)

1.2 SMF-MZI的构成及工作原理

MZI由两种单模光纤组成(如图2所示),自相似脉冲经过第1个耦合器后被分成两个脉冲,与非线性环形镜不同,两个分脉冲分别进入不同的物理路径,通过改变双臂的参数可以破坏MZI的平衡,从而得到自相位调制感应相移,实现光开关功能。

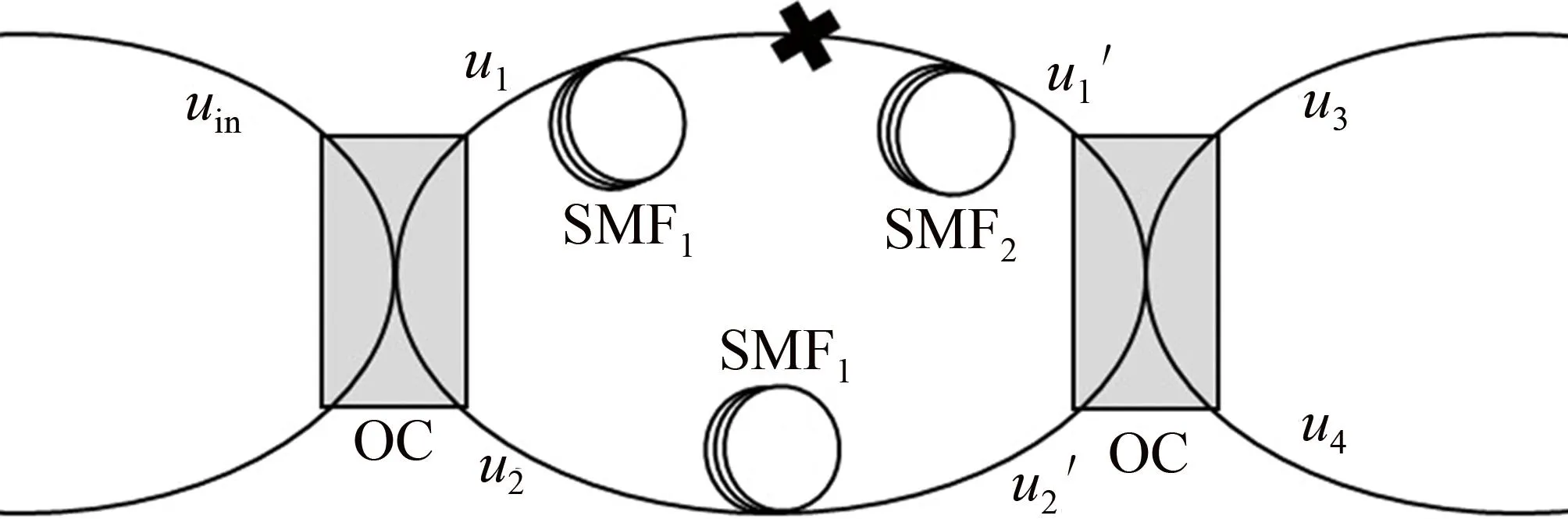
图2 马赫-曾德尔干涉仪结构图

本文中设计了一个非对称的MZI,输入脉冲经过第1个耦合器后进入上下臂的两路脉冲的光信号振幅为u1和u2如下式所示[24]：

(8)

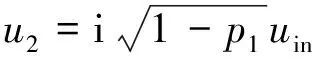
(9)

式中,p1为第1个耦合器的功分比,uin为自相似脉冲包络的慢变振幅。两脉冲在MZI中传输并于第2个耦合器处发生干涉,两个输出端口的振幅u3和u4分别为：

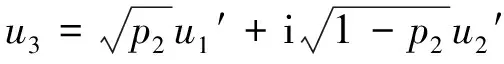
(10)

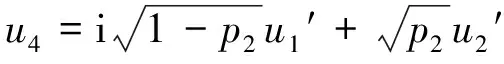
(11)

式中,u1′为上臂输出脉冲的振幅,u2′为下臂输出脉冲的振幅,u3为输出的压缩脉冲的振幅,u4则为脉座的振幅,p2为第2个耦合器的功分比。

MZI的上臂采取SMF级联的方法,能够使脉冲在保证峰值功率增大的前提下,减小脉宽。关于SMF1和SMF2的最佳长度选取规则如下：上臂的脉冲在到达第2个耦合器时的脉宽最窄,峰值功率最高;下臂的光纤长度要使第2个耦合器干涉后输出的脉座最小。

2 数值模拟与分析

2.1 激光器的自相似演化过程

采用低功率的高斯脉冲作为抽运光源,为了能够更好地反馈脉冲在自相似激光器中的演化过程,抽运光源的中心波长采用光纤通信的常用波长。将一个半峰全宽(full width at half maximum,FWHM)为2.8 ps、峰值功率为10-10W以及中心波长为1550 nm的高斯脉冲输入到自相似锁模激光器,循环30圈后获得自相似脉冲输出,如图3所示。

图3 自相似锁模激光器输出脉冲

从图3a可以看出,高斯脉冲在激光器的前几圈演化过程中,由于初始的峰值功率较小,波形图变化不明显,随后脉冲峰值功率突然急剧增加后降低,这是因为脉冲在循环的过程中受到大量自相位调制感应频率啁啾的作用,较弱的色散效应会引起脉冲整形,整个激光器腔的净色散呈正色散,脉冲展宽,脉冲的前后沿变陡。随着循环次数的增加,脉冲的前后沿逐渐变缓,脉冲趋于稳定,达到自相似锁模脉冲的输出条件。图3b所示的啁啾线性部分也是突然减小后增大的过程。从图3c脉冲的频谱图可以看出,相比于前5圈,第6和第7圈频谱的强度突然增大,由于入射的高斯脉冲为无啁啾的,随着圈数的增加,自相位调制产生的频率分量展宽了频谱,频谱的振荡峰的个数增加,且最外层的峰的强度最大。在第21圈后,从时域图可以看出脉冲波形呈抛物线型,脉冲频谱与脉冲的时域形状相关,振荡的结构变得不明显,最后几圈的频谱趋于一个强度较低且稳定的抛物线型。最终从激光器中获得了峰值功率和半峰全宽分别为26.9941 W和4.044 ps的自相似脉冲。

进一步引入自相似因子S来衡量激光器输出的脉冲是否符合自相似脉冲的演化要求,如下式所示[25]：

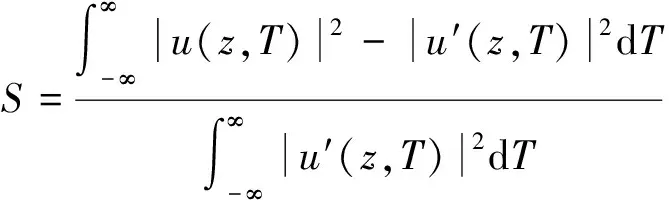
(12)

式中,u(z,T)为数值仿真的激光器输出脉冲的包络振幅,u′(z,T)为具有与u(z,T)相同的峰值功率和半峰全宽的抛物线脉冲。根据多次仿真模拟,当S≤0.1时,输出脉冲符合自相似脉冲的演化要求。经过计算,输出脉冲的自相似因子为0.04,符合自相似脉冲的要求。最终输出的自相似脉冲和抛物线脉冲的波形及啁啾如图3d所示。

2.2 MZI压缩部分

采用两种单模光纤来构建MZI,两种单模光纤的区别在于2阶色散的值,SMF1和SMF2的β2分别为-20 ps2/km和-1.25 ps2/km,两个耦合器的功分比均为0.55。

2.2.1 SMF1的最优长度设计 分脉冲u1在上臂上传输是为了获得峰值功率较高和脉宽较窄的压缩脉冲,确定了耦合器的功分比,将u1在SMF1中传输,可以获得传输过程的时域图。如图4a所示,脉冲的脉宽随着传输距离的增大而逐渐变窄,峰值功率在z=8.16 m达到最高后急剧下降。

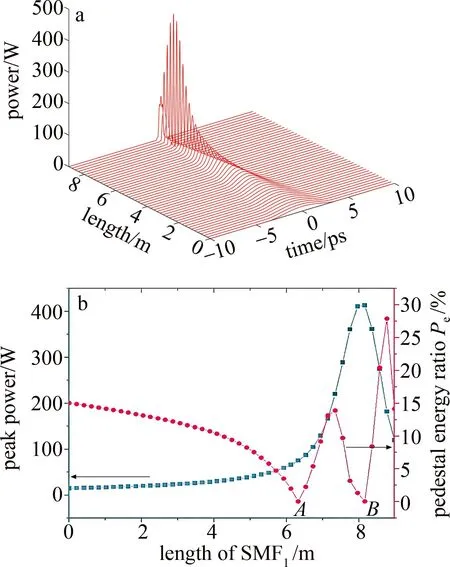
图4 a—SMF1的时域演化图 b—峰值功率和基座能量曲线图

引入基座能量比例Pe来评价脉冲基座的大小,基座能量比例Pe是传输脉冲的总能量与双曲正割脉冲总能量的相对差值,双曲正割脉冲是与输出脉冲具有相同峰值功率和的无基座脉冲。基座能量比例的表达式如下式所示[26]：

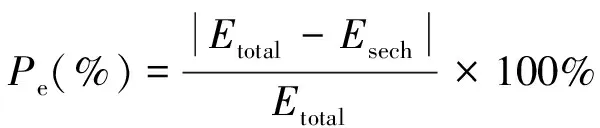
(13)

式中,Esech=2PpeakTFWHM/1.763代表双曲正割脉冲能量,Ppeak为双曲正割脉冲的峰值功率,TFWHM表示双曲正割脉冲的半峰全宽,Etotal是一个常量,代表传输脉冲的总能量。经计算,锁模激光器输出的自相似脉冲的基座能量比例为15.0354%,当脉冲的总能量越接近双曲正割脉冲时,Pe越小,说明输出脉冲得到基座能量越小。

从图4b可以看出,脉冲的峰值功率随着传输距离的增加而增大,基座能量比例曲线存在两个极小值,分别是0.0431%(在6.324 m处)和0.0543%(在8.160 m处),针对这两个点(A和B)来讨论脉冲后续在SMF2的传输特性。

将这两个脉冲传输到足够长的SMF2中,脉冲的时域图如图5所示。红色虚线和黑色实线区域分别为脉冲在SMF1和SMF2中的演化过程,两组脉冲在SMF2的峰值功率呈现周期性地增大后减小的趋势,关于两组脉冲在SMF2的峰值功率最高处的数据如表1所示。相比于极小值点A,极小值点B达到其最大峰值功率所需的SMF2更短,脉宽更窄,基座能量比例更小,脉冲的整体质量更高,更有利于后期输出压缩脉冲。

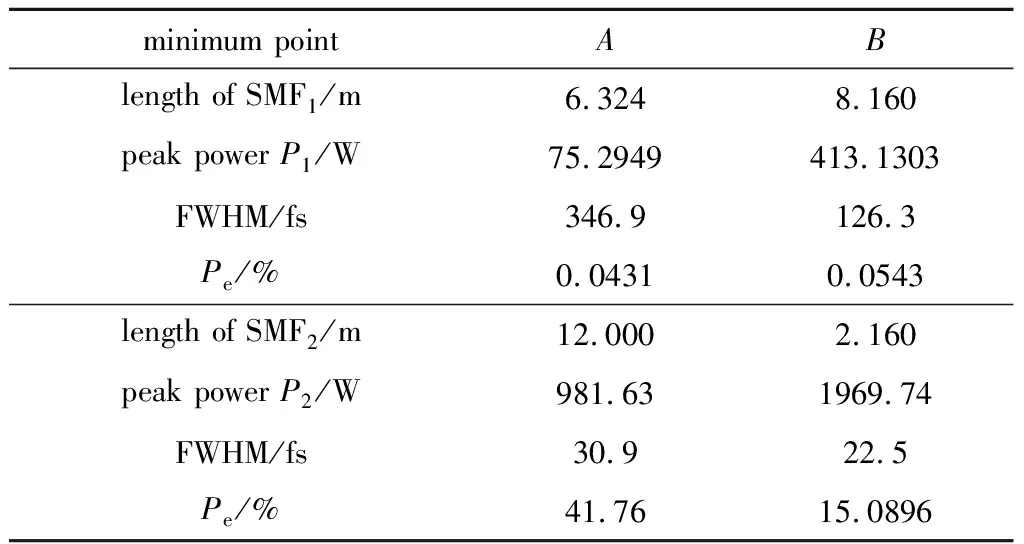
表1 极小值点A和B对应的光纤长度和输出脉冲的参数

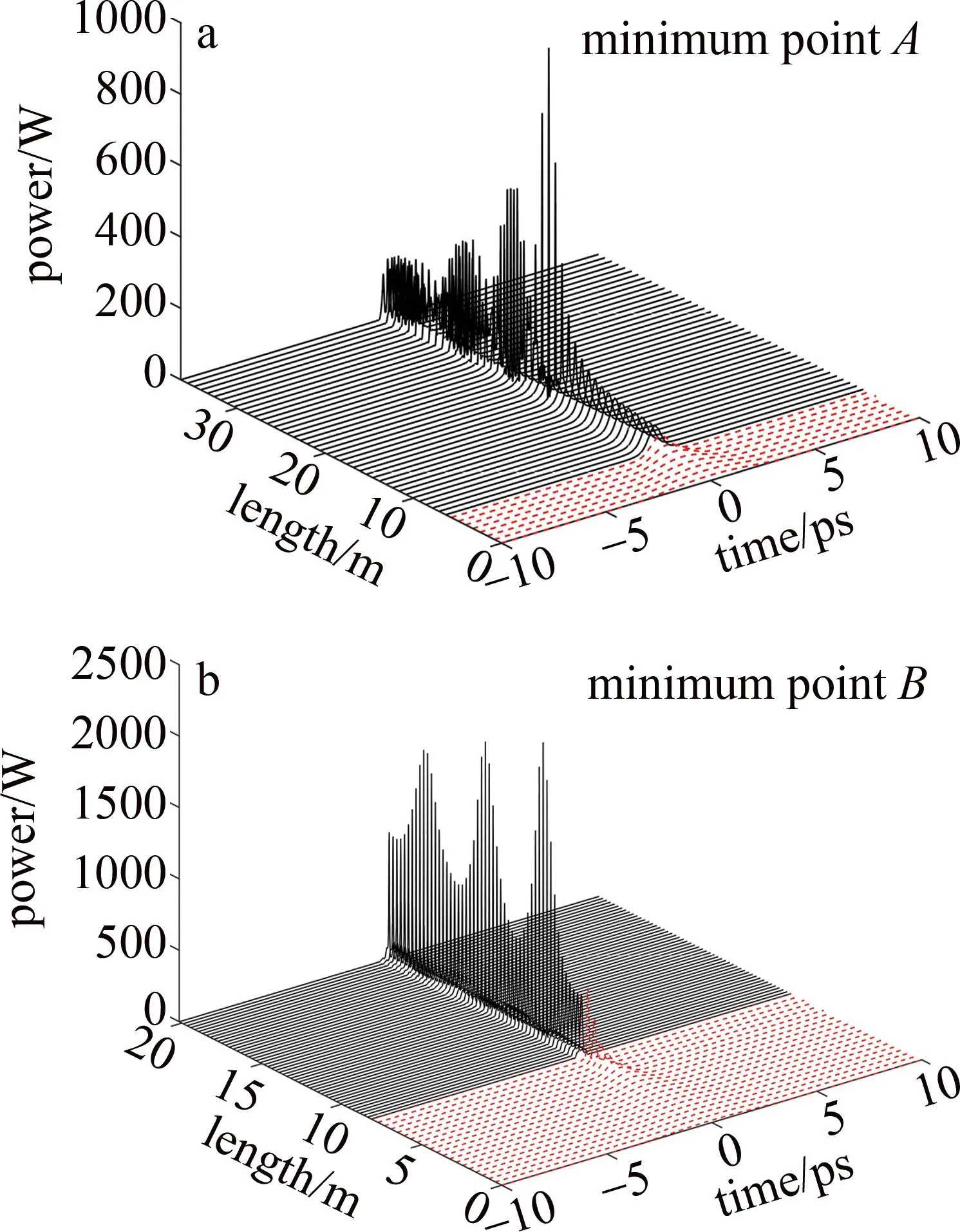
图5 SMF2的时域图

2.2.2 SMF2的长度变化对压缩脉冲的影响 为了得到质量更高的压缩脉冲,在保持耦合器功分比不变以及上下臂的SMF1长度保持一致的前提下,调整SMF2的长度,观察在特定光纤长度内脉冲参数的变化。已知脉冲在SMF2的传输过程如图5b所示,脉冲演化过程中最大峰值功率出现在z=2.160 m处,选取1.296 m～3.024 m区间的SMF2长度来分析SMF2对后期输出压缩脉冲的影响。表2中为在SMF2的区间均等分所选取的数据点,便于分析各个点对应脉冲的差异。

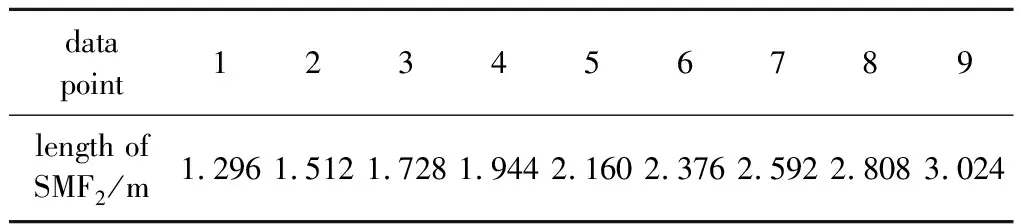
表2 数据点所对应的SMF2长度

图6a显示了对应SMF2长度u1′和u3的峰值功率大小。通过对比SMF2的输出脉冲u1′和最终获得的压缩脉冲u3,两个脉冲峰值功率曲线都是先增大后减小的走势,可以发现,在2.160 m(即第6个数据点)前,压缩脉冲的峰值功率要高于上臂的输出脉冲, 2.160 m之后压缩脉冲的峰值功率降低至200 W以下。如图6b所示,从u1′的演化趋势可以看出,在随着光纤长度的增加,脉冲先被压缩后展宽,与峰值功率曲线的演化趋势相反,在2.592 m前,压缩脉冲的脉宽要大于u1′,这是因为下臂的输出脉冲脉宽较大,两个脉冲相互干涉后,脉冲的基座部分通过干涉相消的方法去除,脉冲的中央部分干涉相长。 图6c为基座能量比例曲线。表明了压缩脉冲的基座明显比未干涉前要小,且两条曲线的差值从较大变为较小,在2.160 m前,上臂的脉冲峰值功率增大的同时基座能量比例减小,前6个数据点的压缩脉冲能够保持在10.5%以下。

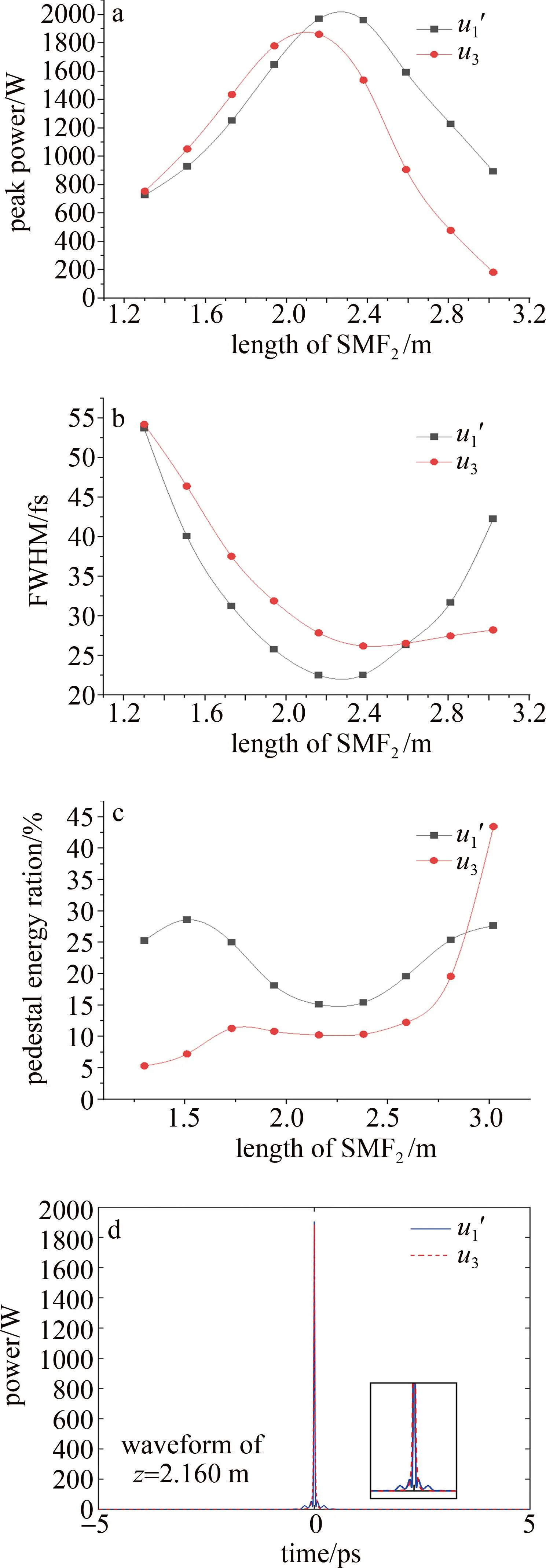
图6 上臂的输出脉冲与压缩脉冲

用压缩品质因子Q来综合评价压缩脉冲质量[27]：

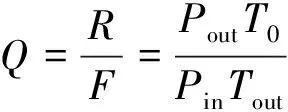
(14)

式中,品质因子R是输出脉冲与输入脉冲的峰值功率比,Pin为上臂输入脉冲的峰值功率,Pout为压缩脉冲的峰值功率,压缩因子F是输出脉冲与输入脉冲半峰全宽的比值,Tout为压缩脉冲的半峰全宽,T0为上臂输入脉冲的半峰全宽,Q越大,压缩效果越好。

从图7中可以看出,脉冲的压缩品质因子曲线存在极大值,位于光纤长度2.16 m处,因此,该长度的SMF2经过耦合器干涉后输出的脉冲压缩效果最好。

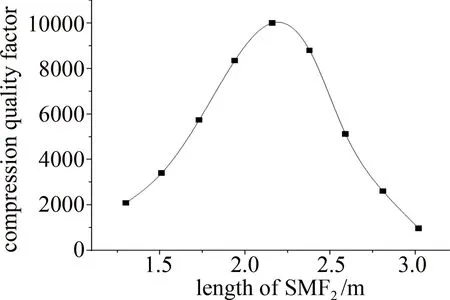
图7 不同SMF2长度对应的压缩品质因子曲线

2.2.3 高阶色散对压缩脉冲的影响 输入脉冲在单模光纤中传输存在脉宽小于1 ps的情况,即使β2≠0,也必须包含β3项,这是因为参量Δω/ω0(Δω为谱宽,ω0为中心频率)没有足够小到可把β3项简而化之。脉冲在SMF中传输特性用包含3阶色散的非线性薛定谔方程表示：

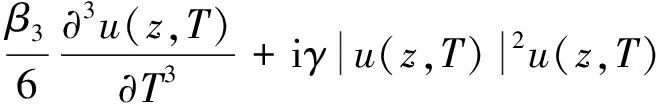
(15)

式中,β3为3阶色散系数,等号的右侧分别代表着2阶色散、3阶色散和非线性效应。取3阶色散系数为0.01 ps3/km,图8为考虑3阶色散的上臂脉冲演化的时域波形图和上臂输出脉冲与压缩脉冲的对比波形图。

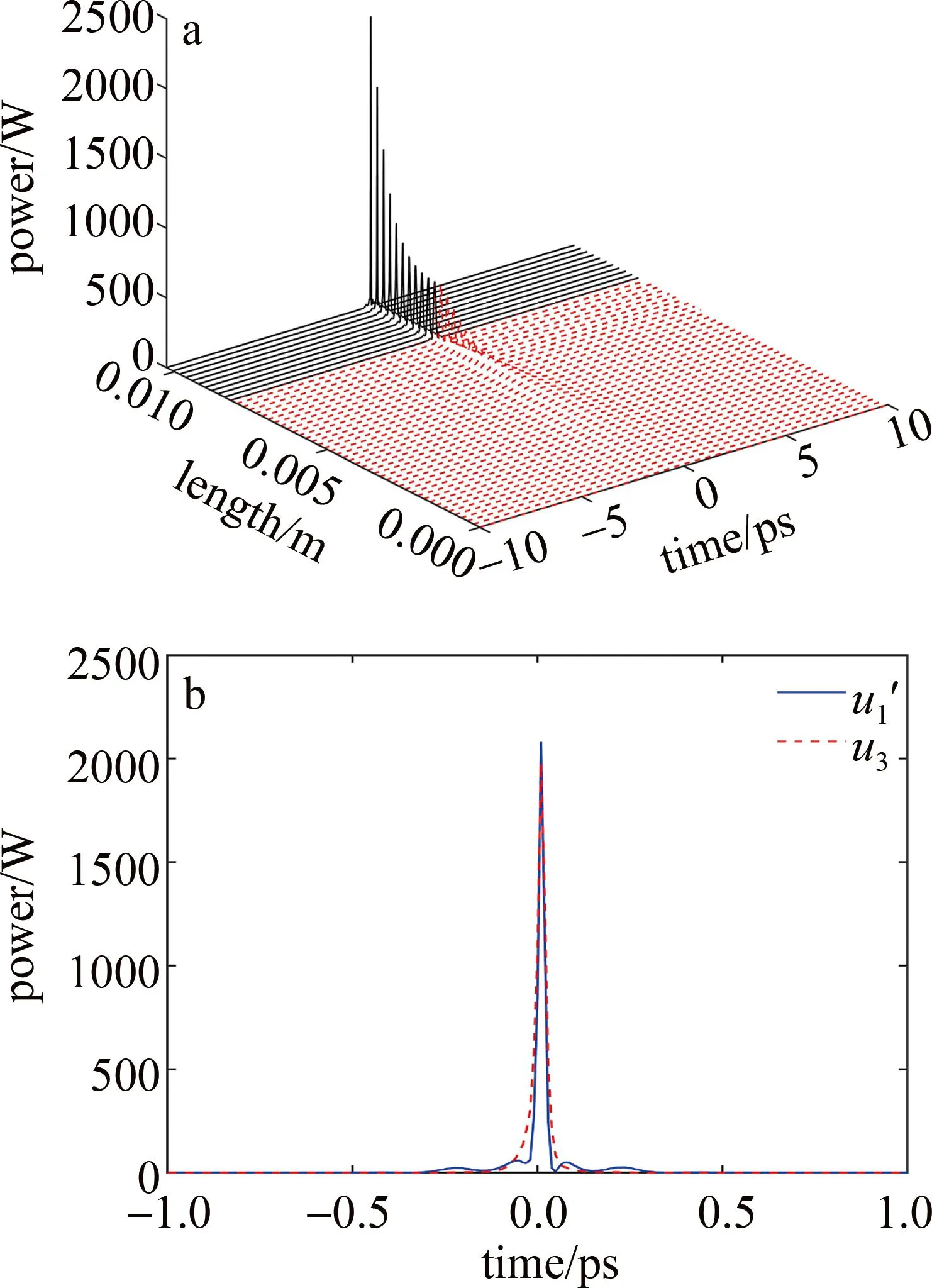
图8 a—上臂的输出时域图 b—输出脉冲与压缩脉冲的波形图

从图8a可以看出,脉冲的峰值功率相比于只考虑2阶色散有所提升,但是3阶色散效应会使脉冲的波形不再对称,且产生带有振荡结构的拖尾。从基座上分析,SMF1段输出脉冲的基座能量比例仅为0.1104%,在SMF2中压缩,基座能量比例增长至2.9114%,通过耦合器的干涉作用,上下臂的脉冲相互干涉,最后输出的压缩脉冲的基座能量比例高达至17.653%,干涉仪没有达到减小基座的要求。这是因为脉冲的3阶色散给脉冲带来位移,上下臂的输出脉冲中心不在同一直线上,从压缩脉冲的波形图可以得知脉冲的前沿变缓,后沿的基座得到有效的消除。

以0.001 ps3/km为步长,将3阶色散系数从0取到0.01 ps3/km,对应的压缩脉冲的峰值功率、半峰全宽以及基座能量比例曲线如图9所示。3阶色散系数的增大对压缩脉冲的峰值功率增长有一定程度的抑制。半峰全宽曲线在3阶色散系数较小的时候呈现较缓的增长,当3阶色散系数大于0.004 ps3/km时,脉宽不断减小。基座能量比例曲线的最低点出现在0.001 ps3/km处,随着3阶色散系数的增大,曲线出现小范围的减小,但基座能量比例均大于11%,为了减少3阶色散对压缩脉冲的影响,3阶色散系数应小于0.001 ps3/km。

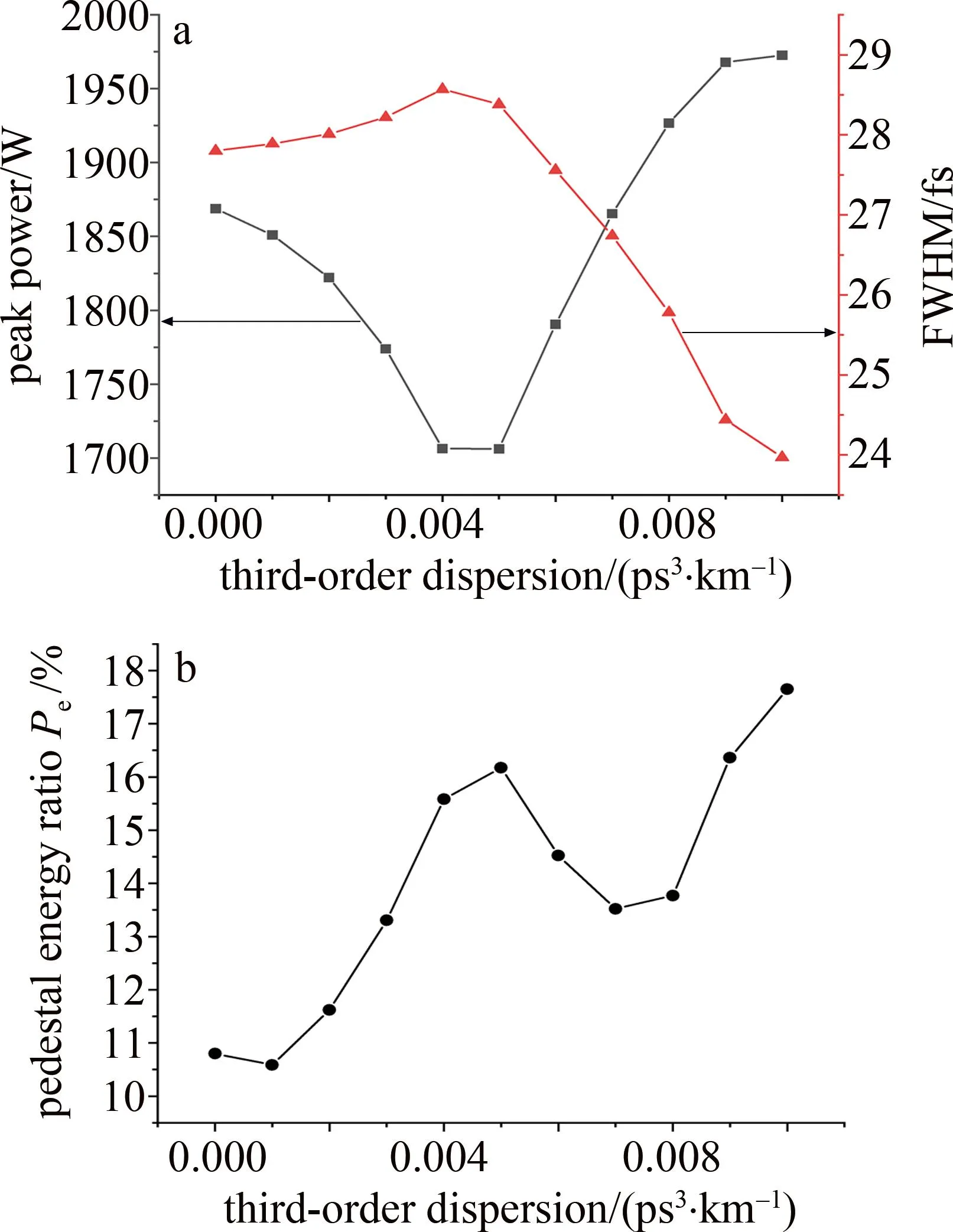
图9 不同3阶色散系数下压缩脉冲有关参数曲线

3 结 论

基于分步傅里叶法对非线性薛定谔方程进行求解,并且建立自相似锁模激光器和马赫-曾德尔干涉仪的数值模型,研究了自相似脉冲在马赫-曾德尔干涉仪的传输特性。研究结果表明,上臂采取级联单模光纤的方式可以获得峰值功率较高的脉冲,上下臂的输出脉冲通过耦合器后脉冲中央部分干涉相长,基座部分干涉相消,最后获得一个峰值功率高、基座能量比例小的超短脉冲。上臂两段单模光纤的优化设计主要是通过分析脉冲在不同长度的峰值功率、半峰全宽和基座能量比例,确定第1段单模光纤的长度为8.16 m,结合压缩品质因子,第2段单模光纤的长度为2.16 m时的压缩品质因子最好。在光纤传输过程中,高阶色散会影响脉冲的形状畸变,数值仿真发现脉冲右移,脉冲非对称并伴随着前后沿振荡,上臂的脉冲在传输过程中基座能量一直处于增大的趋势,最后耦合器输出的压缩脉冲的基座能量比例高达17.653%。研究结果表明,高阶色散较大会影响脉冲压缩质量,当3阶色散系数小于0.001 ps3/km时,能输出质量较好的压缩脉冲。