一种线结构光平面的标定方法

李忠祥,周哲海,2*,陈 丽 ,赵 爽,李 勇

(1.北京信息科技大学 机械工业现代光电测试技术重点实验室,北京 100192;2.北京信息科技大学 光电测试技术及仪器教育部重点实验室,北京 100192)

引 言

近些年来,线结构光3维测量系统因其结构简单、稳定度高、效率高、量程大、非接触等优势,在3维模型重建、物体3维轮廓检测、逆向工程等领域获得了广泛应用,体现出了相当广阔的应用前景[1-3]。在线结构光3维测量系统中,测量的精度主要取决于系统标定的精度,而线结构光的光平面标定是系统标定中的关键部分[4-5]。

现有的光平面标定法主要分为矢量法[6-7]、几何法[8-9]和数学计算法[10-12]3种类型。其中,矢量法是使用向量叉乘的思想来求解光平面的坐标,该方法计算速度较快,实际操作也相对简单,但是精度相对较低。几何法是利用几何思维来求解光平面的方程,随着研究的不断深入,许多新的方法被不断提出,例如,LI等人[13]使用一组设计好的正交平面,并在两个平面上绘制两组平行线,首尾相连可以得到多个直角三角形,将光条照射在各个平面上,直角三角形的光条长短关系使用交比不变原理可获取交点的坐标值,最后使用非线性优化获得最终结果;PAN等人[14]提出的一种基于条纹点位置不确定性补偿的交比不变方法,最终标定精度的均方根 (root mean square,RMS)可以达到0.4 mm;CHEN等人[15]也提出了一种基于光束整形系统和交比不变方法的光平面标定方法,可以使被测物的轮廓扫描测量精度达到0.005 mm。数学计算法是这3种方法中运算量最大且基本不需要获取光条上特征点信息的一种方法,LIU等人[10]提出的基于联立多个光条在相机坐标系中的Plǜcker矩阵求解光平面方程的方法,精度RMS达到了0.009 mm;ZHANG等人[16]提出了一种基于Plǜcker矩阵的多传感器全局校准方法,该方法通过优化不同位置的光条中心点,并设置基准视觉传感器来校准其它传感器,误差小于0.05 mm,但总体上该方法计算量过大且流程复杂。除此之外,学者们还提出了一些新方法,例如使用3维靶标的光平面标定方法[17-18],以及为了解决自动扫描问题而提出的一些基于主动视觉[19]或使用振镜[20-22]和旋转机构[23]来标定的方法。但这些方法要么依赖3维标定靶的加工精度,要么依赖振镜和旋转机构运动的线性度,因此导致操作复杂,且要获得较高精度时的成本较高。

为了解决上述问题与不足,本文作者提出了一种新的基于几何法的线结构光平面标定方法。该方法使用线结构光光条上所有中心点来拟合光条在像素坐标系下的直线方程,并将该直线与标定靶标之间连成的直线相交,得到交线的像素坐标P0(u,v)。利用投影几何原理可知,该交点连接相机光心后,必定交沿相机坐标系Zc轴方向一定距离处的投影平面α于一点E″。建立该交点E″与P0(u,v)之间的数学关系,联立标定靶所在平面的相机坐标系下数学表达式,即可求解得到每个交点P0(u,v)的相机坐标系值,多次移动标定靶,获取多组交点的相机坐标值,通过最小二乘拟合即可得到相机坐标系下光平面的方程。结果表明,本文中提出的方法在干扰较大或光条特性不明显的地方(如光条两端或相机视野两边处), 仍能获得较高的测量精度。该标定方法在简化了标定流程和计算量的同时,具有较高的稳定性、准确性和精度,适用于一般工业应用场景。

1 标定方法

1.1 相机标定及各坐标系之间的关系

在进行线结构光平面标定之前,需要先将单目相机进行内外参数的标定[24]。这里把相机看成一个小孔成像模型,由此可以得到世界坐标系中的一个点A(Xw,Yw,Zw)与相机光心之间的关系,如图1所示。

在图1中,把世界坐标系描述为Ow-XwYwZw,相机坐标系描述为Oc-XcYcZc,图像坐标系描述为O-xy,像素坐标系描述为O-uv。所以由刚体变换可以得到世界坐标系中的点A(Xw,Yw,Zw)转换到相机坐标系Ac(Xc,Yc,Zc)的过程如下：

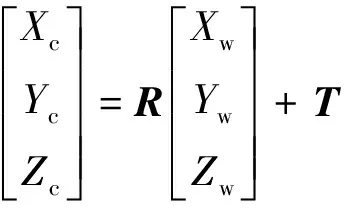
(1)

式中,R为描述刚体变换的旋转矩阵,T为平移向量;点Ac由相机坐标转换到图像坐标系O-xy时可以描述为：

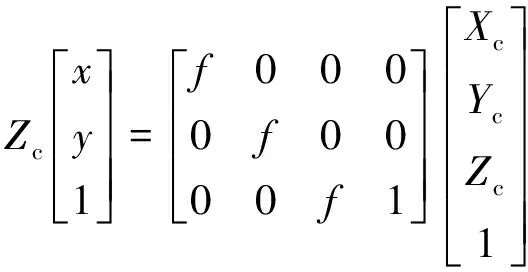
(2)

式中,f为焦距。在图像坐标系转换到像素坐标系时需要注意的是,像素坐标原点通常表示在图片的左上角,而图像坐标原点却在图片的正中间,所以图像坐标系到像素坐标系之间的转换关系为：

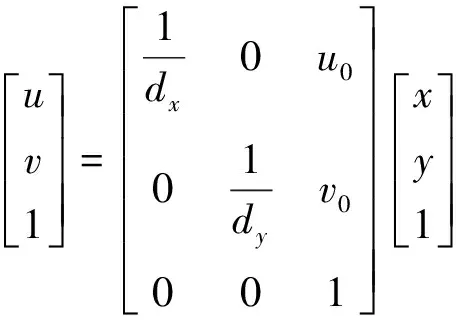
(3)

式中,dx、dy表示单个像素的像元大小,u0、v0表示在像素坐标系下主点位置的偏移量。得到各个坐标系之间的转换关系,可以用ZHANG[24]提出的相机标定方法进行相机标定,这样就得到了上面各式之间相互转换所要的相机内、外参数矩阵。

1.2 标定靶在相机坐标系下方程求解

假设有一点B(Xw,1,Yw,1,Zw,1)在世界坐标系下的标定靶平面上,并且将世界坐标系建立在了标定靶平面上,则可以把标定靶标所在的世界坐标系下平面方程描述为：

MXw,1+NYw,1+PZw,1+Q=0

(4)

式中,M、N、P、Q为常数。由(1)式可以得到该平面在相机坐标系下的表达式为：

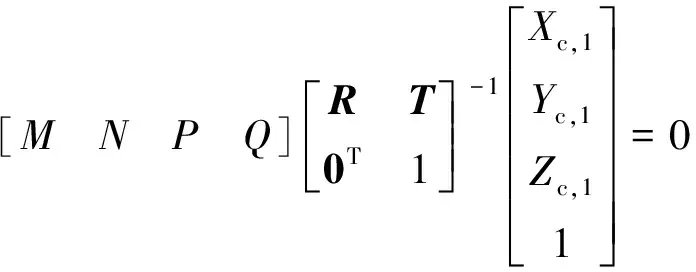
(5)

因为世界坐标系建立在了标定靶平面上,所以(4)式可以转变为Zw,1=0。由此可以推出在相机坐标系下表示为：

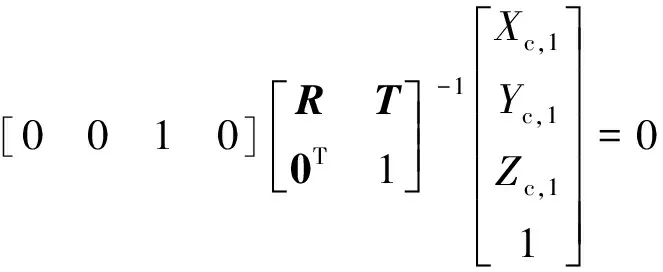
(6)

观察(5)式可知,R,T是在相机标定时求出的每个标定靶不同位姿的平移旋转矩阵,这样可以唯一确定在不同位姿下各个标定靶所在平面的相机坐标系下的方程为：

M1Xc,1+N1Yc,1+P1Zc,1+Q1=0

(7)

式中,M1、N1、P1、Q1是可求常数。

1.3 交点相机坐标计算与光平面标定

使用光条中心亚像素提取算法[25]计算光条亚像素中心,结果如图2所示,这里使用的标定靶是一种圆形标定靶。对提取的所有亚像素中心点使用随机抽样一致(random sample consensus,RANSAC)进行直线拟合,可以得到较为精确的线结构光光线的直线方程λn,将其描述为：

图2 光条中心提取结果

a0u+b0v+c0=0

(8)

式中,a0,b0和c0为直线方程λn的常数项。因为使用的标定靶是圆形标定靶,所以可以很好地得到每个圆形圆心的像素坐标,进而得到每个圆心连线的直线方程Ln,如图3a所示。

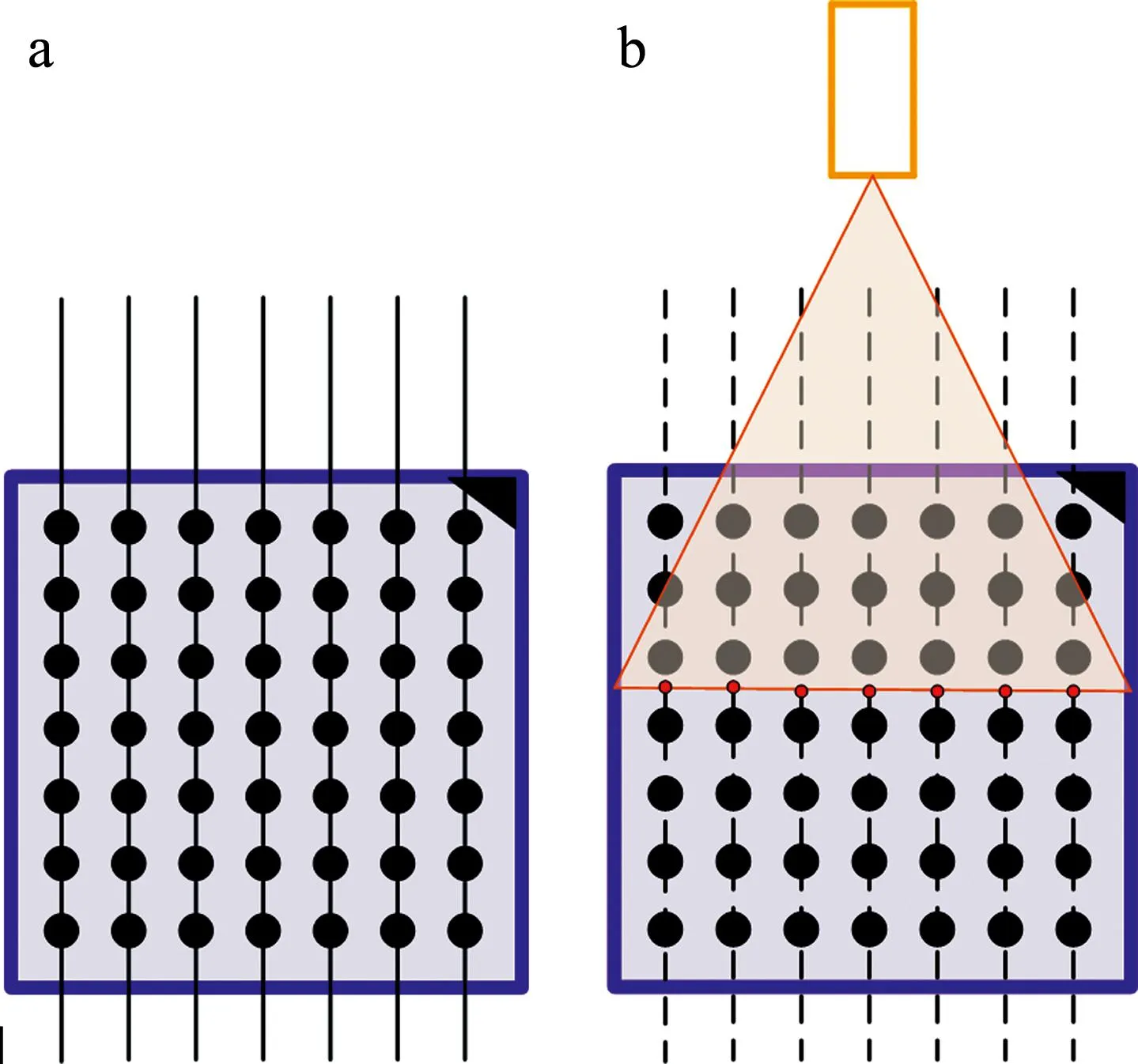
图3 标定靶圆心连线与光条相交

Ln可以表示为：

a1u+b1v+c1=0

(9)

式中,a1,b1和c1为直线方程Ln的常数项。如图3b所示,进一步将光条与圆心连线相交的交点P0(u,v)表示为：

(10)

由相机的透视投影模型可知,在相机视野范围内的标定板上所有点与相机光心的连线都与标定板有且仅有一个交点。所以由(2)式,光条与靶标连线的交点P0(u,v)在相机坐标系下可描述为：

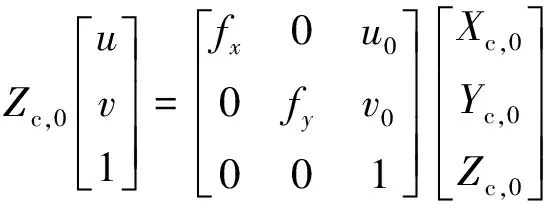
(11)

式中,(Xc,0,Yc,0,Zc,0)T表示相机坐标系下的交点的坐标值,其系数矩阵为相机标定时获取的相机内参矩阵,而fx、fy表示相机在u、v轴向的尺度因子,u0、v0表示选取的主点坐标。将(11)式中的相机内参矩阵求逆后左乘至等号左边,可得到如下关系式：

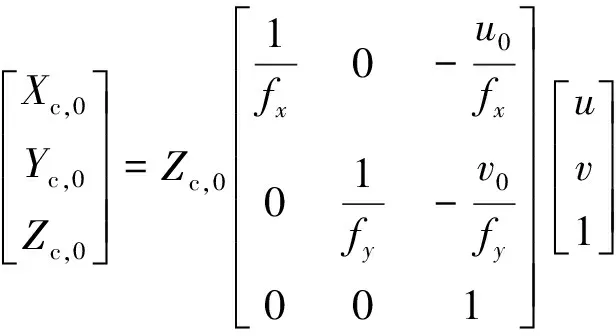
(12)

经过化简,(12)式进一步表示为：

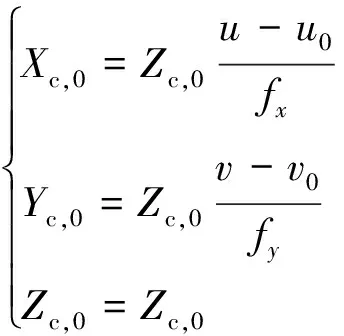
(13)

标定板上两线的交点透视投影模型如图4所示。通过分析可知,距离相机光心一定距离处的,图像坐标系α中点E″的图像坐标与相机光心的连线和世界坐标系下,该点与相机光心的连线共线。

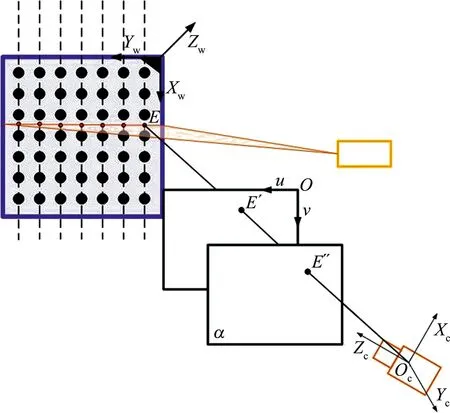
图4 标定板上两线的交点透视投影模型

所以,相机坐标系与离相机光心一定距离处的图像坐标系α之间的旋转矩阵R为单位阵,并且平移向量T=(0,0,g)T,其中g为常数。进而得到在坐标系α中两线交点的相机坐标值为：

(14)

为了方便计算,这里设g=1, (14) 式简化为：

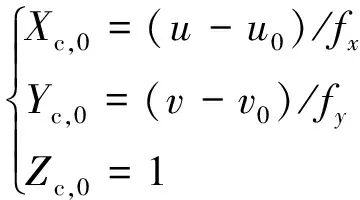
(15)

所以,图2中E点的投影坐标E″与相机光心Oc所组成的直线方程为：

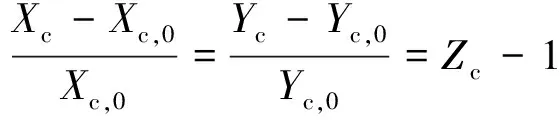
(16)

联立(7)式、(10)式和(16)式,得到E点在相机坐标系下的坐标为：

(17)

式中,等号右边均为已知量,a0、a1、b0、b1、c0、c1可由N个不同位姿标定板上的光条直线方程与靶标连线的7条直线方程得到。使光平面固定不变,移动N次标定板获取N×7个交点,即可使用最小二乘法拟合得到光平面方程。

2 系统搭建及实验结果

2.1 系统搭建

为了测试光平面标定的精度以及算法的稳定性,设计并搭建了如图5所示的线结构光3维测量系统。

图5 搭建的实验系统

系统使用黑白工业相机,并搭配8 mm定焦镜头用于成像。使用波长为405 nm的一字线结构光激光器作为线结构光源,标靶采用图案数量为7×7,靶标圆心距离为2 cm的圆形标靶。

系统标定时,为了使标定更加简便、准确,使用了一种图片相减求差异[26]的方式来定位光条所在区域。在拍摄标定单目相机所需要图片的同时,也打开激光器照射到标定靶上再次拍摄图片,使在标定靶相同位置下,拍摄的这两张照片之间的差异只有光条,这样就完成了光条感兴趣区域(region of interest,ROI)提取。

整个光平面的标定流程大致分为：(a)拍摄标定靶在不同位置的图像;(b)标定单目相机;(c)使用有无线结构光光条的标定靶图片相减后提取光条中心;(d)将光条中心进行直线拟合并求出标定靶圆点与该直线交点的表达式;(e)求出标定靶所在平面的相机坐标系下表达式;(f)求出第1.2节中的(15)式,并联立所有方程组求解交点的相机坐标系下的坐标值;(g)多次移动标定靶求解多个交点的相机坐标系值后,使用最小二乘拟合光平面。具体的标定流程如图6所示。

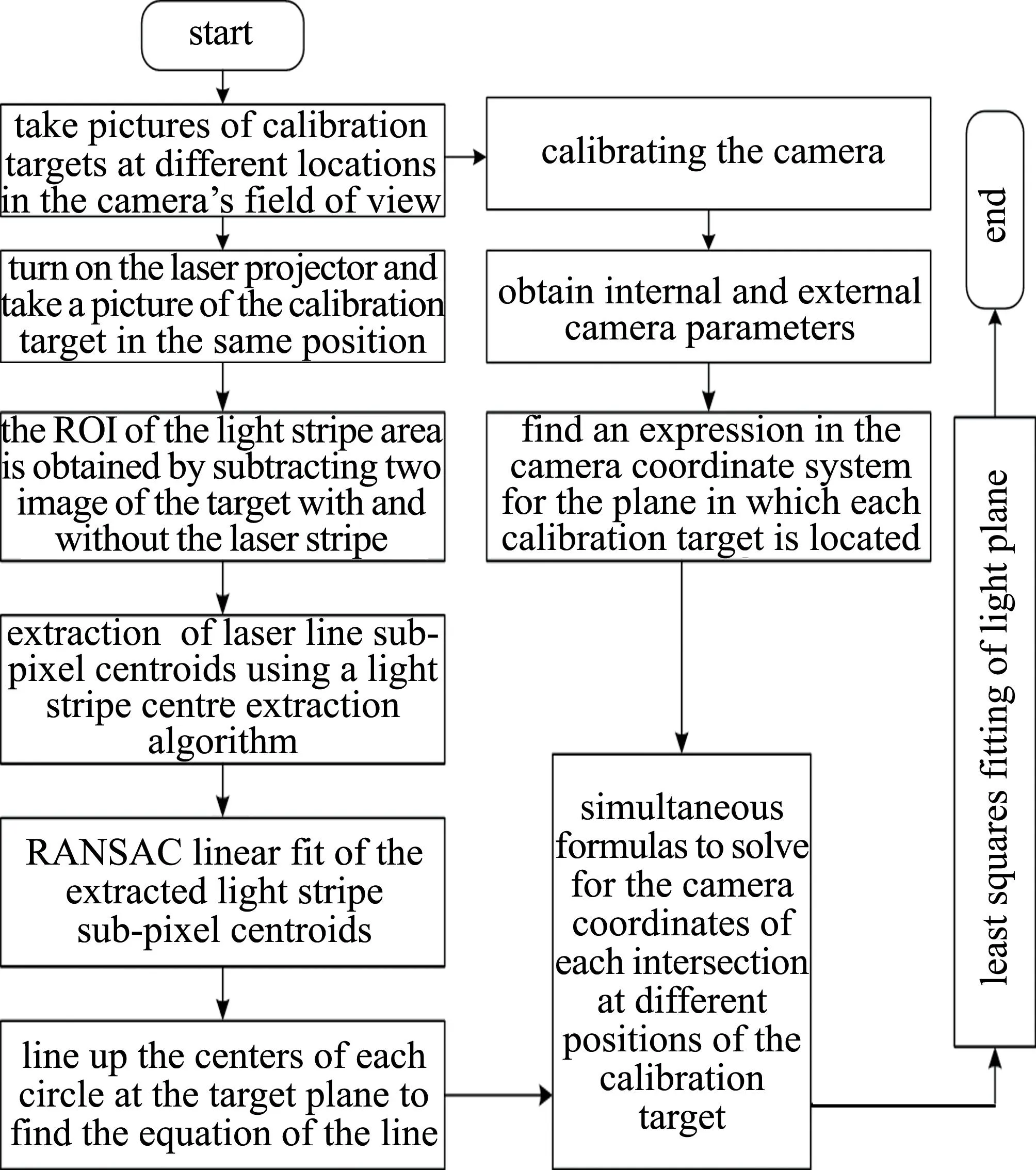
图6 系统标定流程图

2.2 实验结果

移动10次标定靶,拍摄10组有、无光条的标定靶图片,标定得到单目相机的内参矩阵为：

(18)

拍摄的所有标定使用光条如图7a所示;使用光条中心提取算法得到图7b中每个光条对应的中心线。

图7 光条图片与光条中心提取结果

光平面标定结果如图8所示,表达式为：

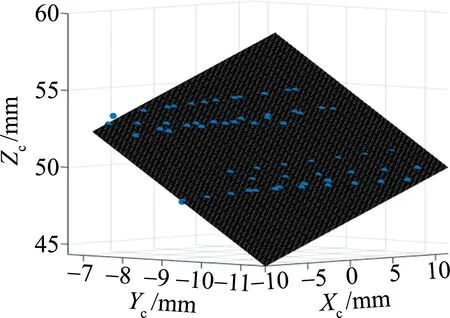
图8 光平面标定结果

Zc=0.260958Xc+1.833015Yc+68.194519

(19)

使用了长度为40 mm的标准量块来测试光平面的标定精度,量块实物图如图9a所示。使用相机拍摄该量块在光条不同位置处的图像如图9b所示,使用光平面标定结果量块上的光条中心点转换为世界坐标并计算量块两端的点距离。

图9 量块实拍图与量块在不同位置的位移情况

表1所示为使用本文作者提出的方法对该量块的测量结果。表中列出了使用本文中的方法和ZHANG[27]提出的方法,分别对该量块在同一光平面下不同位置的16次测量结果。使用ZHANG[27]的方法得到的光平面方程为：

Zc=0.260212Xc+1.833526Yc+68.194689

(20)

而从表2中容易看出,本文中的方法在后10次的光条和相机视野边缘位置处,测量的量块宽度仍能保持较好的鲁棒性。使用ZHANG[27]的方法在光条质量较好、且测量时被测物处于相机成像中心区域内的测量结果略优于本文中的方法,但是在不理想条件下的准确性和鲁棒性均未能达到本文作者所提出方法的性能。

表2 后10次测量结果

表3为测量结果的误差分析。结合表1和表2中的测量结果可知,两种方法在距离相机视野中心并且在激光器出射角中心处的测量误差均较小。在边缘位置对成像不利的条件下,本文作者提出的方法依然能达到相对较高的精度,且RMS误差和平均测量误差也小于对比的方法,证明该方法的抗干扰能力较强,稳定性较好。

表3 误差分析/mm

3 结 论

提出了一种线结构光标定方法,并将该方法与已有的方法进行了对比,得到了更高的测量精度、鲁棒性和稳定性。同时,由于该方法采用先拟合直线后相交的方法,使得光条上干扰点对于拟合光平面的误差可以得到较好的降低,并且所投射的线结构光光条可以在标定靶的任何位置,使得标定更加可控和简便。应用该方法时,在标定时使用到了标定靶的中心点的圆心特征,这样会受到来自标定靶加工精度以及相机畸变程度的影响,这是接下来值得研究的一个问题。