基于混合树的改进泊松曲面重建算法

潘方超,刘 瑾*,杨海马,赵红壮,陈 伟,张 锐,张建伟

(1.上海工程技术大学 电子电气工程学院,上海 201620;2.上海理工大学 光电信息与计算机工程学院,上海 200093;3.中国科学院 空间主动光电技术重点实验室,上海 200083)

引 言

随着现代社会科学技术的不断发展,点云处理与曲面重建技术在各个领域的应用显得日益重要。点云处理与曲面重建技术是文物保护、医工交叉、智慧城市、视觉导航、航空航天等领域不可或缺的技术[1-5]。点云处理技术是3维重建逆向工程重要的一步,其处理结果直接关系后续重建的精确度,而曲面重建就是根据点云处理过后的被测物体完整数据获得其3维表面模型[6]。2006年,KAZHDAN等人[7]首次提出泊松曲面重建算法(Poisson surface reconstruction,PSR),此方案将重建转化为全局问题,通过求解泊松函数并提取等值面完成有向点集的空间重建。此后该团队分别改进原算法为并行泊松曲面重建方法[8]和屏蔽泊松重建算法(screened Poisson surface reconstruction,SPSR)[9],使原算法分别提高了处理速度,降低了时间复杂度。SHEN等人[10]提出一种基于体素感知的重建方法,通过将3维物体分解成多个组件,分块预测重组实现高分辨率表面重建。KAZHDAN等人[11]提出一种包络约束下的泊松曲面重建方法(Poisson surface reconstruction with envelope constraints,PSR-EC),通过施加狄利克雷边界条件,迫使重建的隐函数在这个约束表面之外为零,使缺失数据区域获得了大幅度改进。WEN等人[12]提出一种基于三角面片周长的阈值分割方法,有效避免了重建过程中伪曲面的生成。LI等人[13]提出一种基于移动广义三棱柱的等值面提取算法,有效解决了表面重建过程中等值面提取的剖分二义性和拓扑二义性问题。HUANG等人[14]提出一种法线定向方法,解决了由于点云法向量方向不一致导致重构曲面出现偏差的问题。AMENTA等人[15]提出了一种采用 Voronoi滤波分段线性逼近平滑表面的重建方法,实现对密集采样点云的高精确性表面拓扑重建。ZHOU等人[16]提出了一种引入可见性模型和稠密可见性技术的表面重建,使重建更好地保持场景细节。

以上部分是采用局部拟合、分块预测拓扑关系并拼接成完整表面模型的方法,虽然在局部能取得较好效果,但是不能在全局情况下拟合表面。其余全局方法多是在法点云滤波、向量估计或生成面片等阶段对算法作出优化。本文作者则是在点云存储与搜索阶段提出一种混合树索引方法,平衡了八叉树和二叉树之间的矛盾,在建树过程中逐层记录体素内点云数量以期对局部点云进行密度评估,针对稀疏部分进行不同程度的稠密化,以完成更加精细的重建并提升算法效率。

1 泊松重建与改进

1.1 泊松算法概述

1.2 点云分类与存储

估计3维点云中某点的法向量可以归纳为两个步骤：一是确定某点的特定邻域;二是将该邻域内所有点拟合出最优平面,得到所要估计的法向量。本文中分别在点云存储与搜索阶段进行优化,主要步骤如图1所示。

图1 算法流程图

扫描得来的散乱点云数据分布混乱,消耗内存空间大,对后续处理带来很大困难,因此建立一种简明的点云拓扑关系、高效的存储与搜索方法至关重要。八叉树和二叉树是最常用适用于3维空间点云数据划分存储的方式,其中八叉树算法实现简单、效率高,二叉树在数据邻域搜索比较有优势,四叉树等其它树形结构适用于2维空间以及其它形式数据的处理。鉴于3维点云数据的空间特性与数据量,本文中提出使用基于八叉树和二叉树混合树进行3维空间点云数据的分割与搜索,如图2所示,旨在减小算法的时间复杂度与空间复杂度。

图2 混合树建树示意图

具体做法见下。首先求出点集S所有点云数据的几何中心：

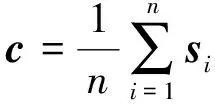
(1)

式中,si表示点集S中第i个点构成的向量,然后求出所有点与中心点c的距离以及所有n个距离的高斯分布,分布在[μ-3σ,μ+3σ]区间内的点集记为S1,[μ-3σ,μ+3σ]区间外的点集记为S2,μ和σ分别为高斯的期望值与标准差。对点集S1和S2分别建立线性八叉树和二叉树进行点云的存储与索引。

为了有效过滤点云集合中的噪声点并平衡滤波与细节保持之间的矛盾,提出以下点云能量模型E1：

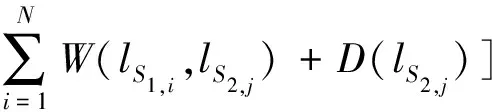
(2)

其中：

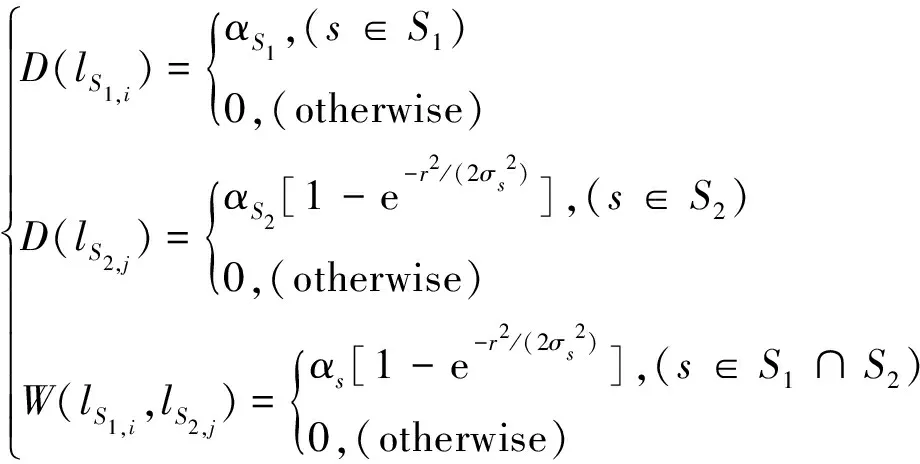
(3)

式中,s是点集S中任意一点,lS1,i表示点集S1中第i点的标签,D(lS1,i)则表示其权重,lS2,j表示点集S2中第j点的标签,D(lS2,j)则表示其权重,W(lS1,i,lS2,j)表示点集S1和S2边缘重合点的能量对,αS1表示点集S1的权重,αS2表示点集S2的权重,αs取αS1或αS2均可,实际计算过程中取为αS1,r表示点到点集中心的距离,σs是松弛系数,N表示点集S1和S2交集中点云个数,权重因子1-exp[-r2/(2σs2)]的作用是削弱边缘点云的能量,起到过滤噪点的作用。

当点云非常密集时,上述能量模型会在两组点云边界处出现二义性,导致重建曲面过程的错误连接,为此引入点云的似然能量E2：

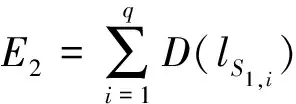
(4)

其中,

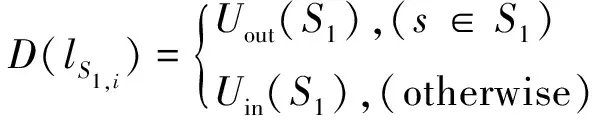
(5)

式中,E2是衡量边缘点云标签分配是否错误的惩戒能量函数,对于S1∩S2内每一个点云,它都具有二义性,用于描述是否在点集内部,遍历点集S1中的q个点,根据点云实际分布选择具体的惩戒能量函数Uout(S1)和Uin(S1)。为了评估标签分配的可能性,引入空间支持函数f(S3)度量点集所在空间的松弛性：

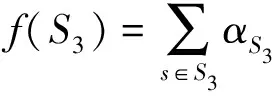
(6)

其中,

S3={s|S1∩S2≠∅}

(7)

为了使f(S3)更好地描述似然能量函数E2,设：

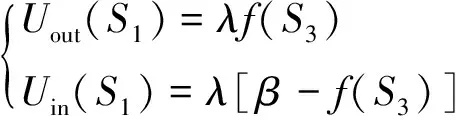
(8)

式中,λ是平衡因子,β是大于所有点f(S3)的常数,令：

E=E1+λ2E2+λ3E3

(9)

式中,λ2和λ3是缩放常数,E是点云的总能量,E3为提高重建表面质量引入的面片能量项,且：

(10)

其中,

wf=1-min{cosφ,cosφ}

(11)

式中,φ和φ是边界某点与两个点集中心点预估平面的夹角。

最后通过Maxflow-Mincut实现总能量的最小化,完成点云的分组存储与滤波。

1.3 法向量估计

法向量估计可以分为两个步骤：一是以某点为中心做适当邻域;二是在此邻域内将所有点拟合一个最佳平面求出法向量。为提高算法输入端点云的法向量精度,本文中算法对法向量估计作如下改进,如图3所示。

图3 法向量估计示意图

求某点s(sx,sy,sz)对应的法向量为ns(nsx,nsy,nsz)。(a)建立以s点为圆心、R为半径的球面：(x-sx)3+(y-sy)3+(z-sz)3=R3;(b)设置初始点云数量统计区间[23i,23(i+1)];(c)判断以s点为中心的23i个最小体素单元是否完全落入球面内;(d)若条件(c)判断为假,将当前值i-1,直至条件(c)判断为真;(e)若条件(c)判断为真,统计球面内点云数量并计算它占样本集内点云总数的比例ri,显然ri取值在区间[0,1]之间,当ri取值在[μ-3σ,μ+3σ]左侧外,认为点云块稀疏,进行针对性稠密化。

对s点所在邻域使用改进移动最小二乘法进行点云的稠密化,将上文所得ri作为移动最小二乘法中的系数向量ri,球面以内区域作为s点的影响区域,拟合函数可表示为：

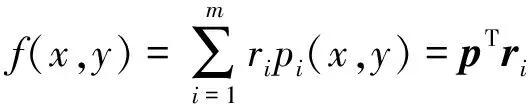
(12)

选用立方基：

pT=(1,x,y,x2,xy,y2,x3,x2y,xy2,y3),

(m=10)

(13)

则拟合函数为：

f(x,y)=r1+r2x+r3y+r4x2+r5xy+

r6y2+r7x3+r8x2y+r9xy2+r10y3

(14)

即：

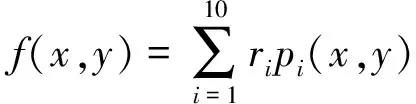
(15)

拟合完成后就可以在s点附近拟合三次曲线对点云进行针对性的插值稠密化。

重新记录稠密化后的邻域点云数量k值。采用奇异值分解(singular value decomposition,SVD)求法向量,首先求该点δ邻域内所有k个点(s1,s2,s3,….sk-1,sk)到s点的向量fi=si-s(i=1,2,…,k)。

设置优化函数：

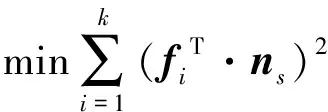
(16)

进一步推导有：

minnsTFFTns

(17)

式中,F由向量组fi构成,上述问题就转化为目标函数的最优化问题,即：

ming(ns)=minnsTQns

(18)

式中,Q=FFT,Q是关于点s3个坐标分量的协方差矩阵。对矩阵F进行SVD分解即可得到s点的法向量,最后通过最小生成树法对所有法向量的方向进行矫正,获得朝向一致的法向量[17-18]。

2 实验结果与分析

为了评价本文中所提重建算法的效果以及与其它不同算法对来自公共数据集进行重建的性能对比,选取了Artec 3D公司的曲轴箱、齿轮、螺丝、涡轮进行算法的比对分析。

2.1 重建细节比较

首先,在建树深度分别为6～10的情况下采用本文中的算法对曲轴箱模型进行表面重建,从图4可以看出,随着树深的增加,模型重建表面精度不断提高,并且在不同树深情况下都表现出较好的效果。可见树深是影响重建效果的重要参数。树深增加,索引到的点云数量增加,重建结果的细节也就更好。

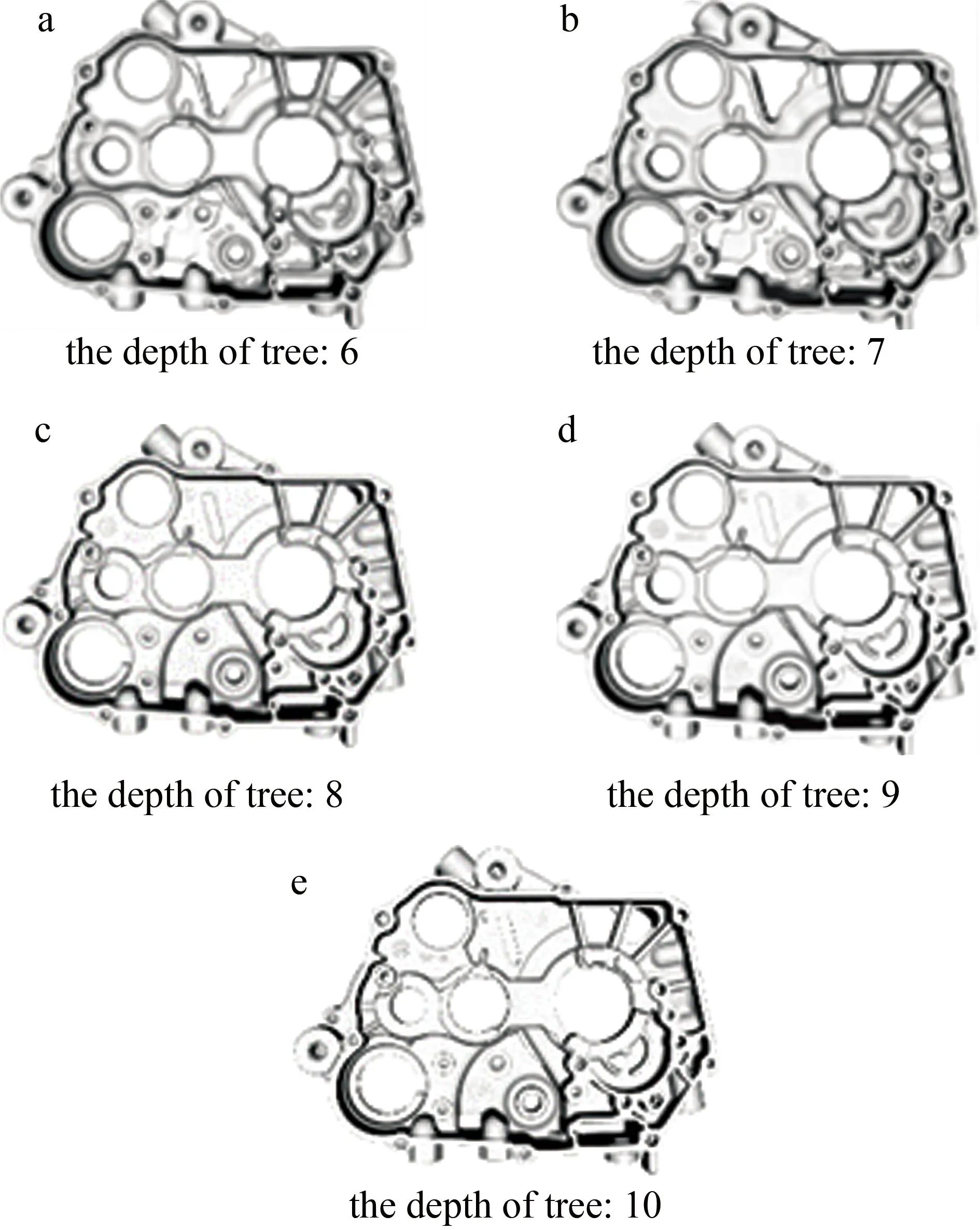
图4 曲轴箱在本文中算法不同树深下的重建效果

在对算法效果的横向比较评价中,选取了PSR算法、SPSR算法、与PSR-EC算法与本文中所提算法进行比较,将每种算法的可变参数调制与所用扫描模型最佳匹配的情况下,各算法重建效果与局部细节放大图如图5所示。PSR算法由于没有引入与模型形态相关的信息,比如扫描过程中的视线信息,导致重建结果在细节方面表现较差。SPSR算法虽然引入了点作为插值约束使重建细节有所改善,但其算法效率仍然不高。SPR-EC算法虽然算法效率较高,但由于表面提取过程中以远离真实解为代价,使得重建表面远离真实模型表面。本文中的算法由于搜索方法的改进使得算法效率明显提高,并且根据前文改进的点云稠密化插值方法针对性地对部分稀疏点云稠密化,结果如表1所示。针对不同模型分别引入了0.86%～1.95%的重建顶点信息,在不影响算法效率的前提下,使法向量估计阶段更加精确,展现出了最佳的重建完整性,更加贴近扫描模型真实表面细节。

表1 各算法重建实际所用顶点数

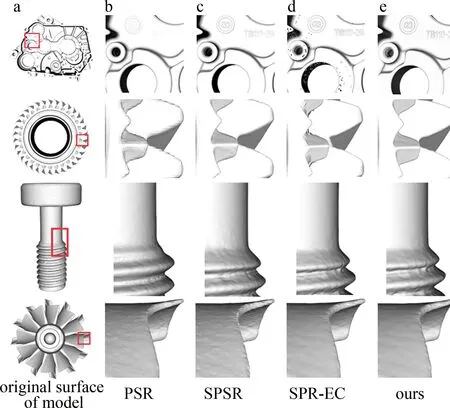
图5 模型在不同算法下最优重建效果与细节对比

2.2 算法效率对比

如图6所示,在算法运行时间对比实验中,随着树深的增加,各算法运行时间呈指数增加。本文中的算法引入点云密度评估,并在法向量估计阶段采用自适应球半径的搜索方法,相比PSR算法与SPSR算法,速度均有明显提高,且在树深值较小时更加显著;相比PSR算法,速度平均提高约33%,比SPSR算法速度平均提高约15%。但由于PSR-EC算法引入了Dirichlet条件作为提取等值面的包络约束,降低了内存开销,本文中的算法与之相比,速度仍然较慢。

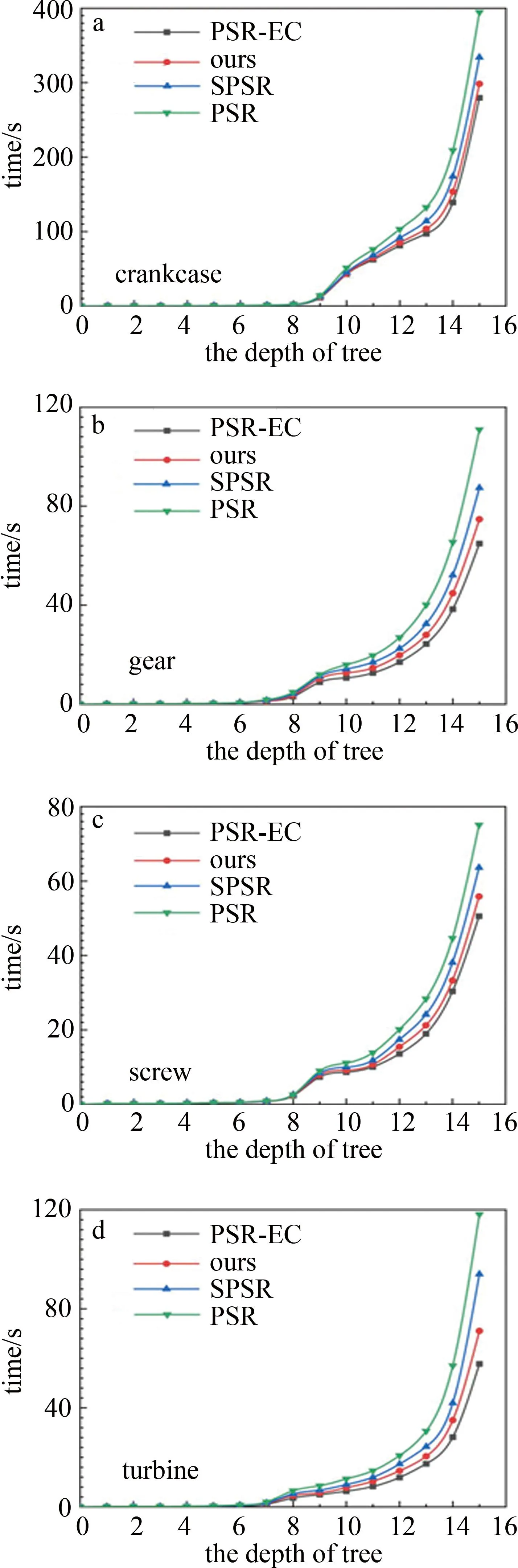
图6 各模型在不同算法下的重建时间对比

2.3 误差评价

此外,由于原始数据与重建后数据有点云模型和网格模型等表示形式,所以,本文中选择原始数据点云形式与重建数据网格形式之间的豪斯多夫距离[19](Hausdorff distance,HD)、原始点云模型到重建表面的均方根误差(root mean square error,RMSE)来定性评价对比实验中各个算法重建表面与原扫描模型表面的差距。将HD和RMSE值分别与此项最大值比较做归一化处理后各算法实测值[20]如图7和图8所示。可以看出,本文中算法的误差在对比实验中最小。

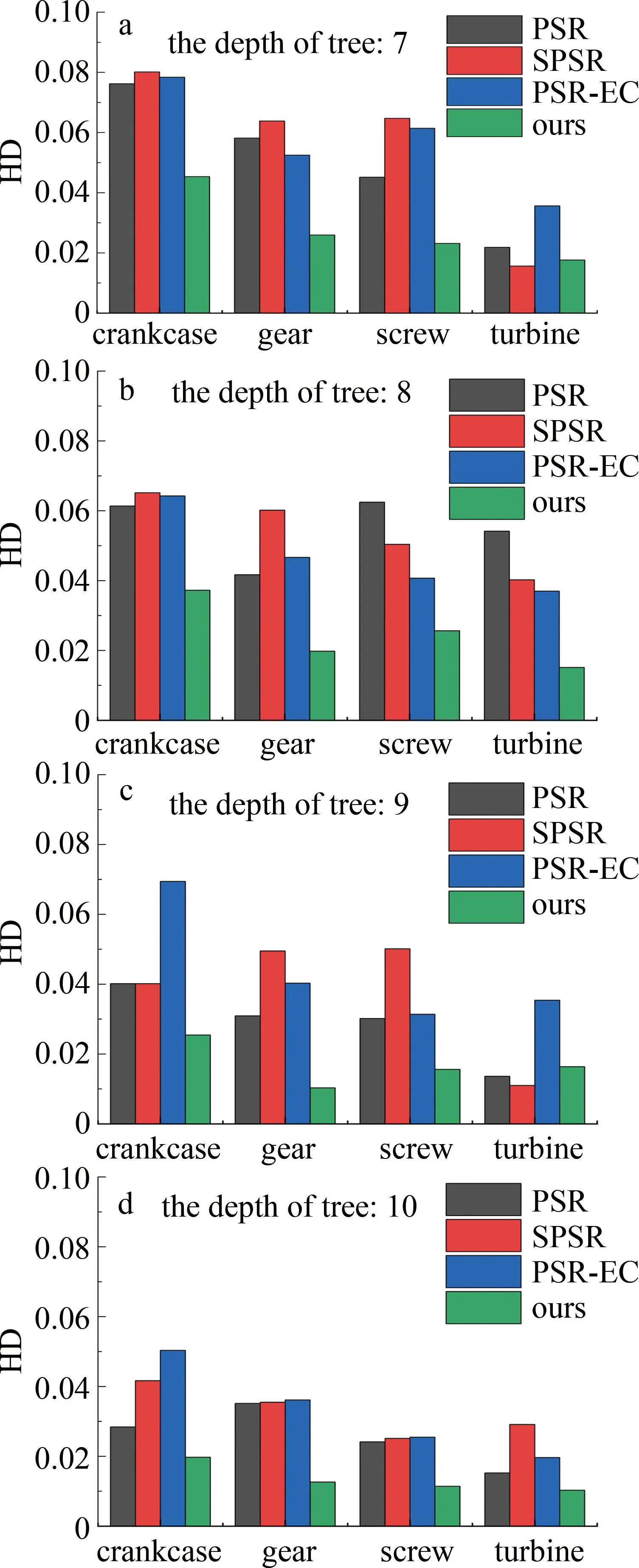
图7 模型在不同算法、不同树深下实测HD值

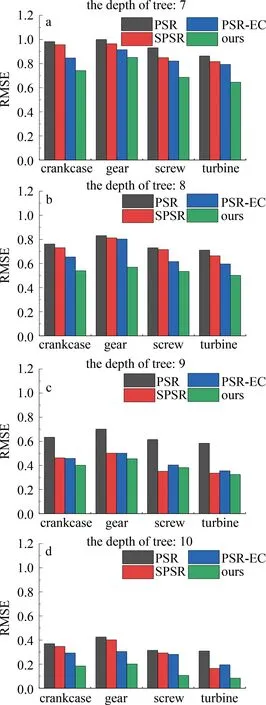
图8 模型在不同算法、不同树深下实测RMSE值

为了更加直观地展现重建表面模型与原始模型的偏差,使用相关软件将重建表面模型与原始模型作3-D比较处理,具体操作方法如下：(a)将原始模型转换为step机械文件格式;(b)将重建表面模型与原始模型导入3-D检测软件;(c)依次执行初始对齐,最佳拟合对齐,3-D比较命令,4组实验中参数设置均相同。

本组设置中设置可显示公差范围为[-0.1 mm,+0.1 mm],可接受公差范围为[-0.01 mm,+0.01 mm],且在此范围内的模型匹配范围显示绿色,模型3-D比较的可视化结果根据各区域实际公差的不同显示不同颜色(参见图9中右侧色条)。在此公差设置下,统计各个算法重建结果在可接受公差范围内的比例、均方根值、平均偏离程度与离散程度来衡量重建结果的准确性,实验结果如图9和表2所示。本文中的算法的各项指标总体表现最优,但有个别模型的平均偏离和离散程度不是最小,原因是部分点云稠密化过程引入了较多的噪点。

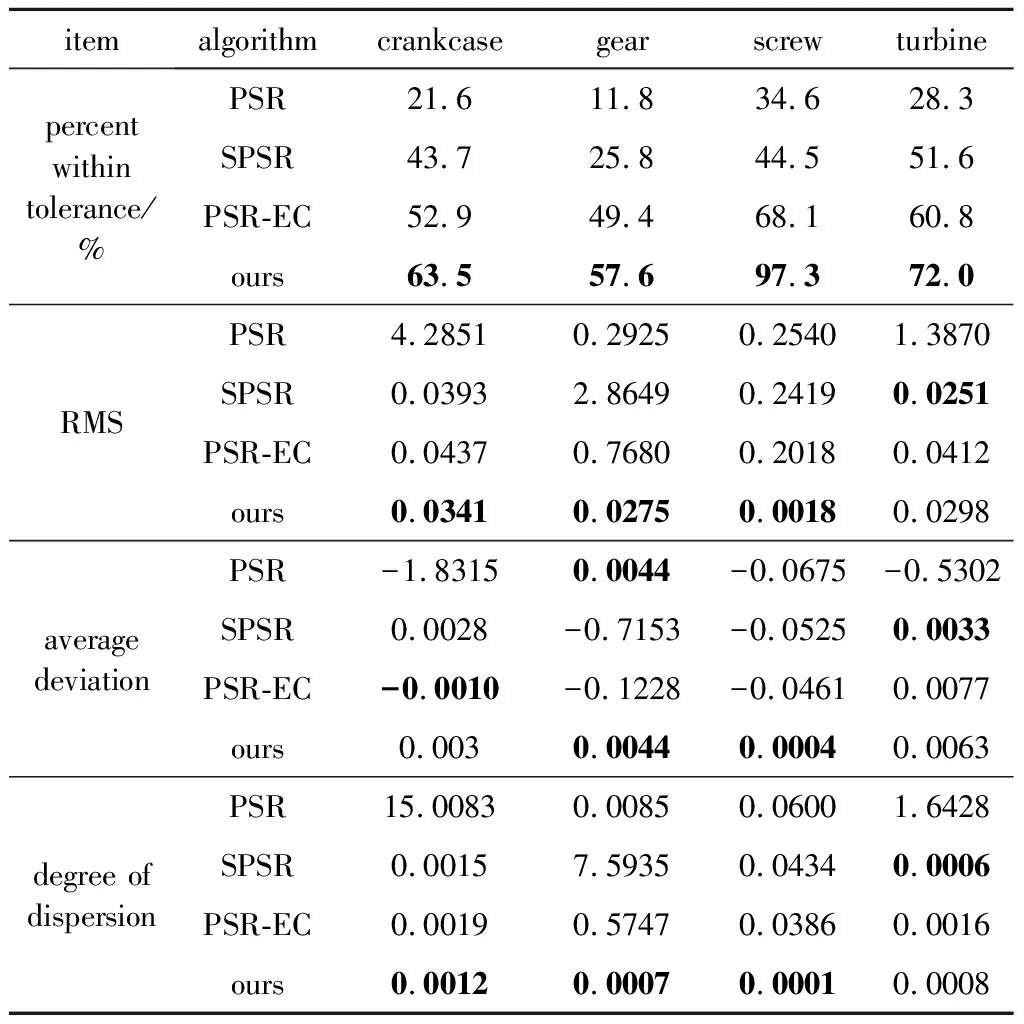
表2 模型误差项实测表

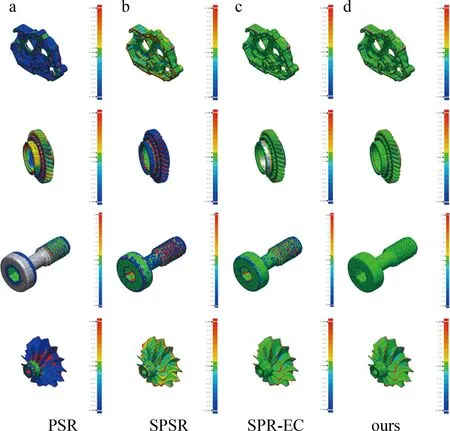
图9 模型在各算法下的重建结果与原模型3-D比较图

3 结 论

从点云的存储与搜索角度出发对泊松重建算法提出了改进,采用一种新的点云搜索方法,提高了算法效率;并根据引入的能量函数对点云进行密度评估,根据统计结果对点云稀疏过程进行针对性的稠密化,使得重建结果细节表现更好。经过在4个不同数据集上的实验对比,本文中算法的处理速度对比泊松表面重建算法和屏蔽泊松算法有较大提高,并且在重建的完整性与精确性总体表现最优,偏离原模型的程度最小,对中小型物体的重建与误差评价具有借鉴意义。下一步工作将针对泊松方程求解过程与约束条件展开研究,以期降低算法的时间复杂度,使重建效率更高。