基于凹面光栅的光谱检测仪性能提升的研究进展

付 翔,乐文冉,王 颖,汪 亚,邹 林,邓志峰,占生宝*

(1.滁州学院 机械与电气工程学院,滁州 239000;2.安庆师范大学 电子工程与智能制造学院,安庆 246133)

引 言

光谱检测以其快速、无损、高效等优点,深受工业、国防、医学、大气、海洋探测等众多领域青睐[1-2],已成为当下检测技术领域研究的热点。其原理是依据成像的光谱组成和强度,鉴别出物质类型、并检测出物质的含量[3-5]。其中,成像的光谱组成会影响被检测物质的类型,光的强度和分辨率会影响被检测物质的含量[6-8]。凹面光栅是光谱检测的重要器件,但其衍射成像由于受自身条件限制,必然出现像差、光谱分辨率不高等问题,影响被检测物质的类型和精度[9-12]。针对上述问题,大量科研工作者从光栅设计、制作入手,对凹面光栅消像差、以及提高分辨率进行了较深入的研究。但从目前的资料来看,这些研究只是零散地分布于各研究文献中,还没有对其进行归纳与总结。本文作者从消除像差和提高分辨率两方面入手,对其所采用的设计技巧进行归类,对提高成像质量的研究进展进行阐述,并总结了阶段性成果。

1 消像差的研究进展

众所周知,光谱检测系统由狭缝、色散元器件、聚焦元器件以及探测器构成,被封闭于一个密闭的检测室内。提高光谱检测精度的重要一环是消除成像的像散、彗差、色畸变、谱线弯曲等。科研人员从单个光栅制作或添加辅助元器件入手,开展了消像差的研究。

1.1 单个凹面光栅的消像差

罗兰型光栅是光谱检测最常用光栅[13]。先重点阐述罗兰型光栅消像散和弧矢彗差、提升检测精度的进展。消像差的基本思路是：以光程函数为基础,将其展开成多项式,再依据所需消除的像差,使某一系数项Fi,j=0。对于一个以原点为中心、法线方向为x轴的凹面光栅系统[14],光程函数可表达为：

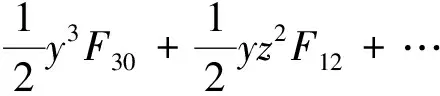
(1)

式中,x,y,z是坐标轴,F20为离焦系数,F02为像散系数,F30为子午彗差系数,F12为弧矢彗差,F00和F10涉及到光栅方程产生,不具备关键像差特征,可忽略。检测时,为提高检测精度,必须消除像散和弧矢彗差,这要求研制光栅过程中,需不断调节记录、使用光源位置,达到F02和F12为零的目标。

使用全息法制作罗兰型光栅,当记录光源波长为λ0时,BROWN等人[15]研究发现：工作波长λ只有满足条件1≤mλ/λ0≤2(m表示衍射级次数)时,才能同时消除λ处的像散、弧矢彗差等;而对于偏离λ的光束,其像散仍然存在。针对该情况,GRANGE[16]运用光线偏离与光程函数导数关系,提出了采用多维参数组求解最小优化函数值的方法,利用该方法,他们设计出一种波长范围在125 nm～185 nm的凹面光栅,结果表明：当光源以最佳角度入射时,在140 nm和170 nm处像散得到消除,而其它波长处的像散也明显降低。

为进一步减小像散,参考文献[17]中提出了利用平面波、柱面波同时记录光栅的方案,如图1所示。图中,激光源发出的球面光束,经偏振分光棱镜(polarization beam splitter,PBS)分光后,其中一束经球面镜形成平面波,另一束经柱面镜形成柱面波,然后将这两束光发射至待刻光栅。由于柱面波的使用,使得臂长RD增大,由此F02得到降低。

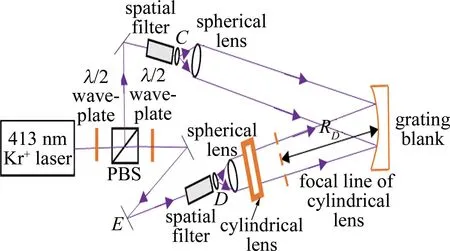
图1 平面波、柱面波记录方案结构示意图[17]

当激光器输出波长为413 nm时,选取365.4 nm作为特征谱线对方案实施前后的效果进行比较,结果如图2所示。可以看出,未校正前,像高接近10 mm,校正后,像高减小到3 mm。实验也进一步证明,该设计思路对于减小像散行之有效[17]。

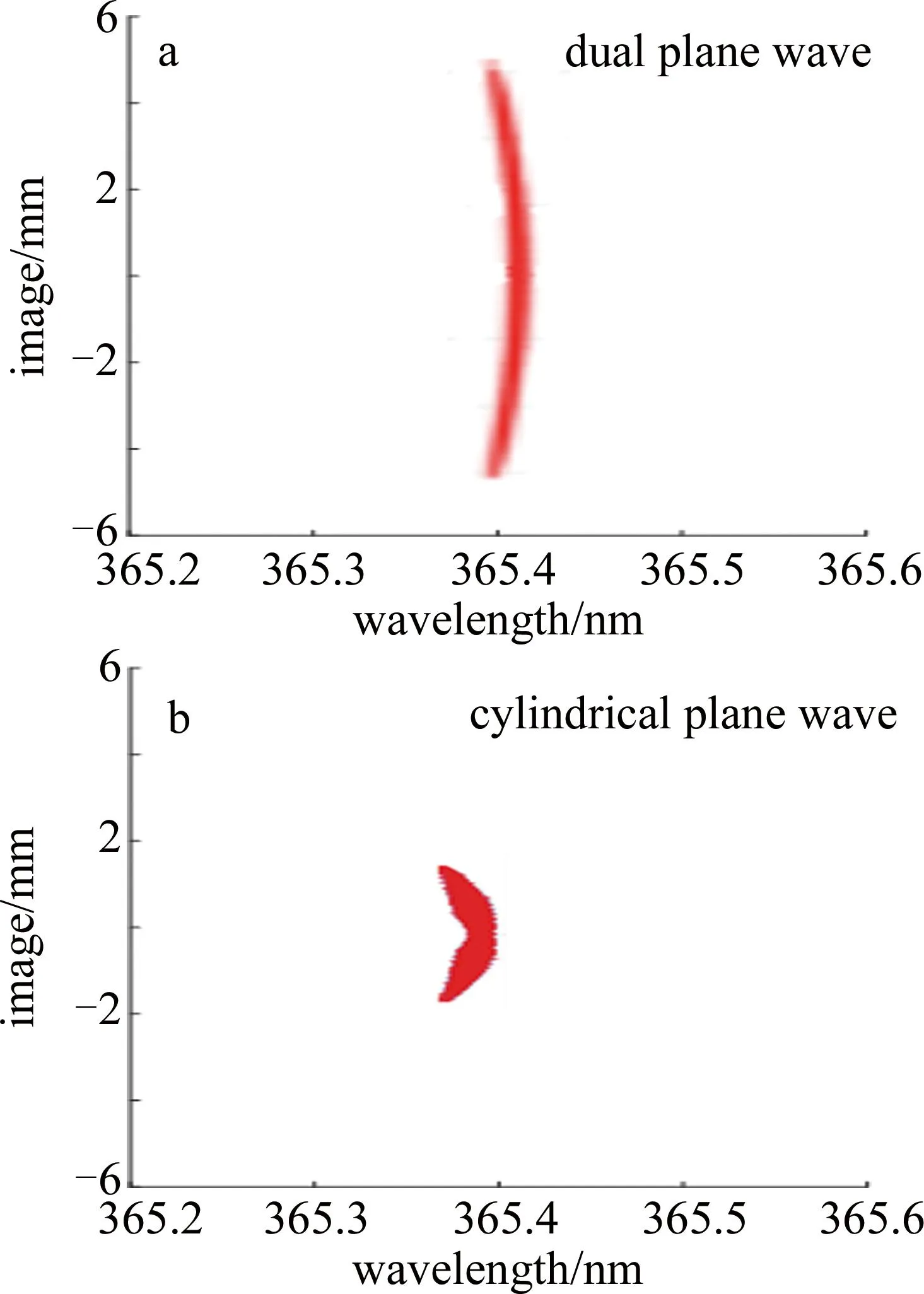
图2 校正前后,波长为365.4 nm处的成像示意图[17]

上述方法虽能减小使用波段像散,但无法校正弧矢彗差。为此,该团队进一步提出利用环面波制作光栅的方案。在上述激光波长不变的情况下,仿真得到圆柱平面波、圆柱环面波记录时的对比结果,如图3所示。可以看出,成像光斑在未校正前为弯曲形状,校正后几乎变成直线,说明弧矢彗差得到了有效抑制。实验结果也证实了理论分析结果的正确性[18]。

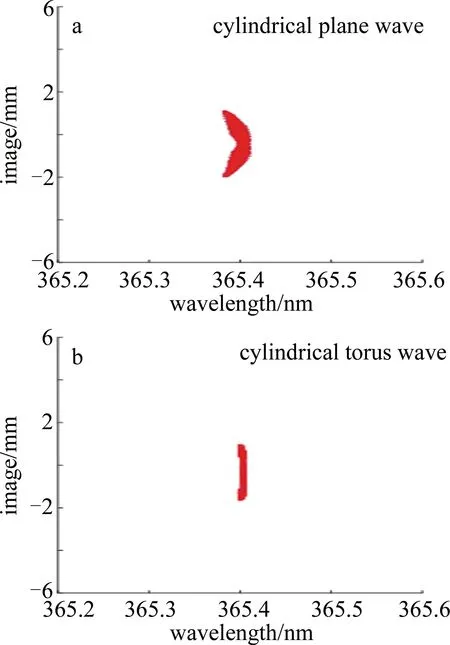
图3 波长为365.4 nm时,圆柱平面波和圆柱环面波成像示意图[18]

除记录光源位于罗兰圆上制作光栅的情形外,还有一种将记录光源置于圆外的制作方案,如图4所示。图中,C、D为置于圆外的记录光源。对于该方案,KONG等人[19]进行了较详细的研究。在假定记录波长λ0=413.1 nm的条件下,通过分析校正波长λ为0 nm～800 nm的成像情况,发现：(a)当入射角、衍射角相等时,像散和弧矢彗差在λ和λ/2处为0;(b)当衍射角为零时,像散和弧矢彗差在λ和2λ处为0;(c)当入射角为零时,像散和弧矢彗差在0和λ处为0。

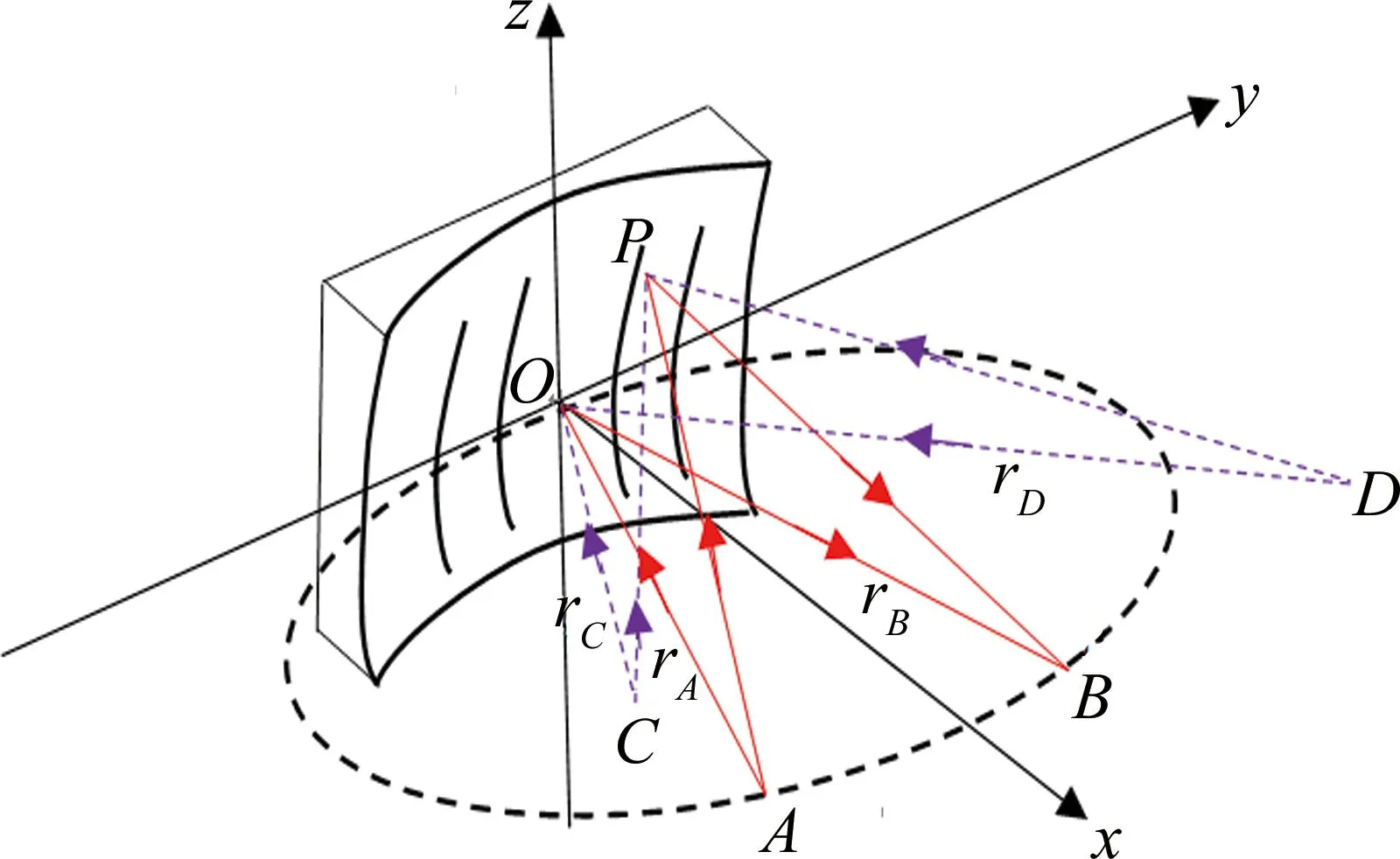
图4 罗兰光栅结构示意图[19]

在以上所有情况下,在两个零像差波长之间的像散和弧矢彗差显著降低。以此为基础,他们给出了一种波长范围为160 nm～600 nm的设计案例,结果表明,当入射角与衍射角相等时,在工作波长为225 nm、450 nm处,像散和弧矢彗差为0;当从点光源发出波长为160 nm、380 nm、600 nm的光束后,经该光栅衍射在像面形成的点列图,相较于传统等刻线密度、曲率半径光栅,像高可从10 mm减小到1 mm,同时谱线弯曲也得到一定改善。

1.2 凹面光栅+辅助器件的消像差

单光栅消像差方案虽能在窄频谱范围内较好地确保低像差成像,但当频谱范围较大时,多波长成像的像散、彗差等仍难以消除。针对该问题,一种双光栅串联的方案被提出[20],如图5所示。图中,光栅G1和G2相切于以O为中心的圆,且对称放置。复合光源发出的光束从狭缝出射,经光栅G1衍射后入射至光栅G2。由于凹面光栅的聚焦特性,相同波长的光束能聚焦于成像面的某一点处。对于该设计,为实现各波长尽可能地无像散、无彗差地成像,需满足如下条件：(a)狭缝必须位于G1的法线上,成像点必须位于G2的法向平面;(b)对于入射光束,要求其不同波长的子光束是平行入射到G2。当满足两个条件时,相同波长的弧矢像距等于子午像距。理论分析时,研究者以波长为 120 nm～170 nm光束为例,通过改变光栅G1衍射角范围,如从40°减小到10°,发现其像散从10-1/rad减小到10-5/rad,彗差从10-2/rad减小到10-4/rad。

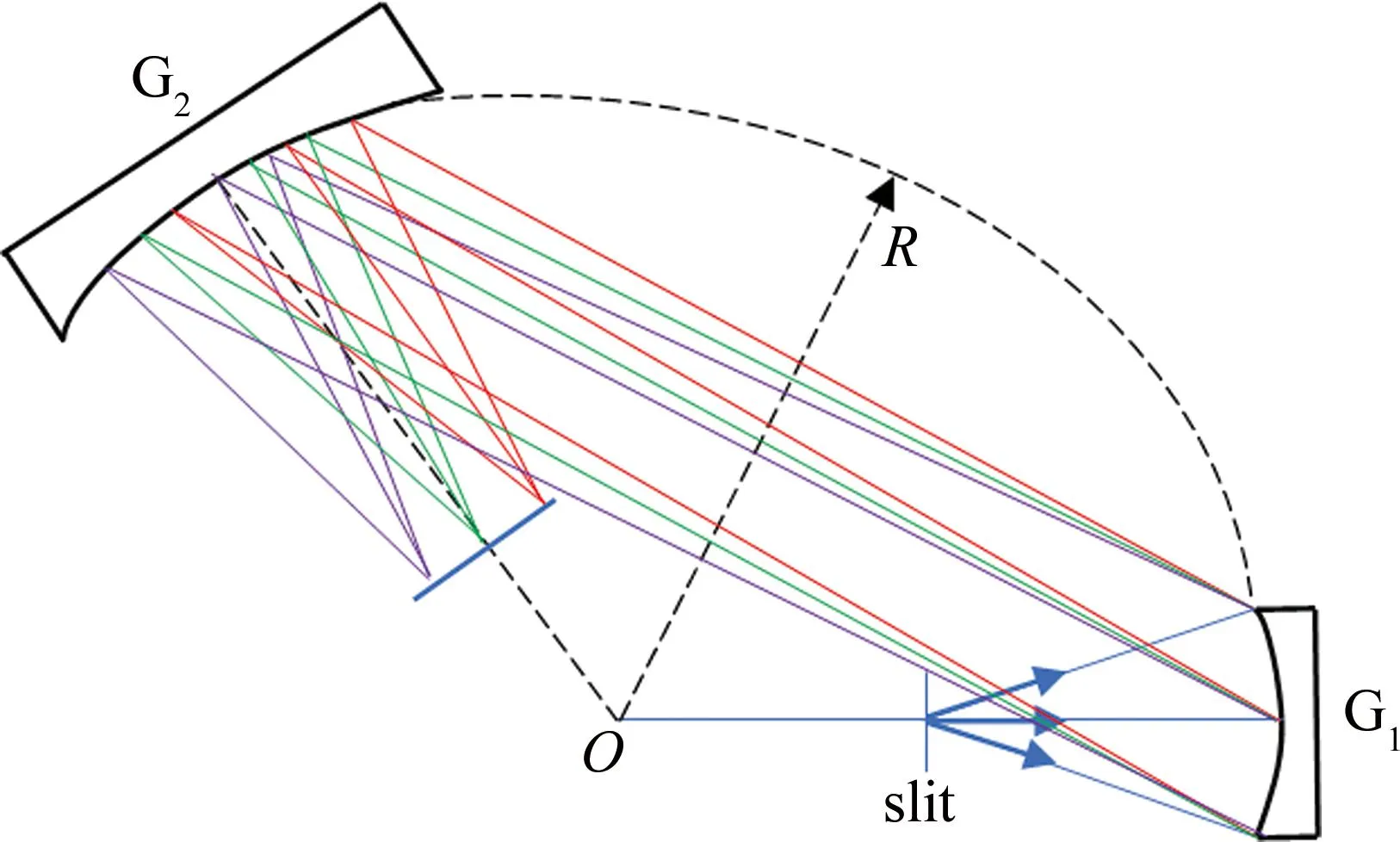
图5 串联光栅架构示意图[20]

上述方案中,由于光栅曲率半径较大,其内切圆半径必然很大,由此导致成像系统的体积较大。针对该问题,参考文献[21]中提出了一种离轴抛物镜串联光栅的方案,如图 6所示。图中,两块离轴抛物镜对称共焦放置。当瞳孔出射的平行光束经离轴抛物镜反射后,必将以平行的方式入射到平面光栅,其衍射后相同波长的光束,必将以平行的方式入射至凹面光栅,满足不同波长子光束是平行入射到凹面光栅的要求。理论分析表明,对于波长为260 nm～380 nm的平行入射光束,当离轴抛物镜半径为200 mm时,系统的成像距离从210 mm减小到101.25 mm。

对于图6所示设计系统,由于使用的元器件较多,必然存在光路对准、像距调节难题。为此,参考文献[22]中提出了一种简化该系统的设计方案,如图7所示。图中,直接以一面离轴抛物镜作为准直镜。由于该镜反射的平行光束入射光栅时,可能导致不同波长的子光束偏离光栅法向平面的情形,为克服这个问题,一块带有楔角的柱面镜嵌入系统,其作用为调节弧矢、子午方向像距,使之满足每个波长无像散、彗差成像的要求。对于该设计方案,理论分析表明：当波长为280 nm～760 nm、柱面镜倾斜角为27.67°、楔角为3.77°时,其光斑均方根半径从图6所示设计系统的11.39 μm降低到8.5 μm。

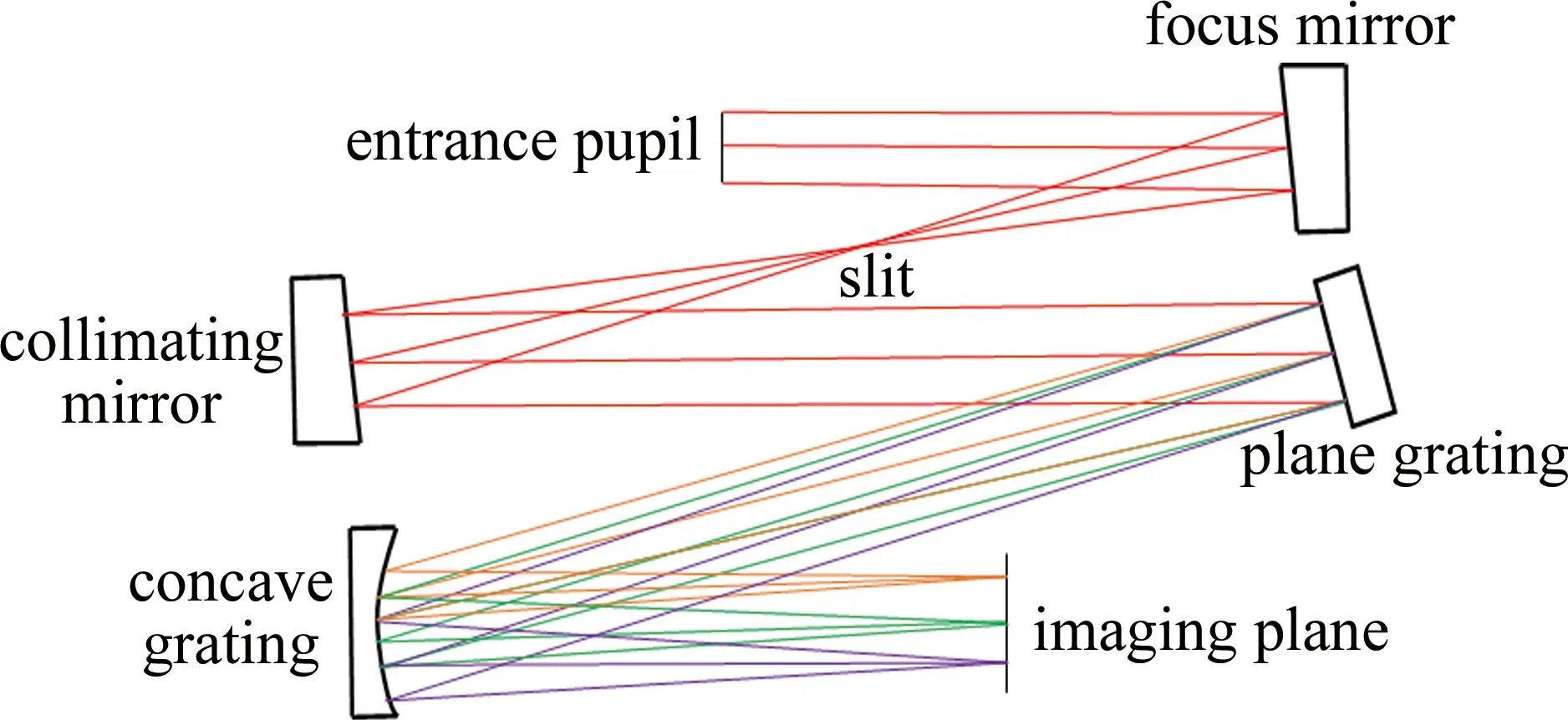
图6 级联光栅像散优化结构示意图[21]

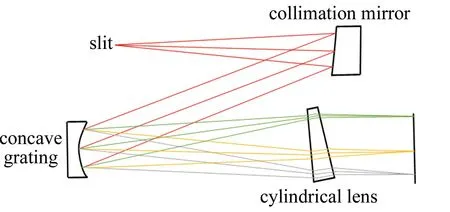
图7 旋转柱面透镜调节像距消像散结构示意图[22]

上述两种设计中,光栅的数值孔径、光束的入射角度要求均较小,这限制了光谱检测的范围。针对该问题,参考文献[23]中提出了柱面镜级联两块凹面光栅,从而拓展检测范围的设计思路。依据每个波长像差校正的原理,首先在满足像散、彗差校正条件下,求解出光栅位置,柱面镜楔角、倾斜角的最优参数,然后针对系统小型化要求,设计出如图8所示大区域检测系统。图中,折叠镜的作用是确保系统在结构紧凑的情况下、进一步减小体积。结果表明：在波长为400 nm～800 nm,第一、二光栅入射角分别为1.2°和15°,柱面镜楔角为15.63°时,其数值孔径达到0.1。

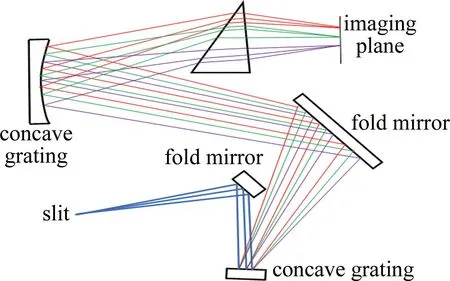
图8 级联光栅型旋转透镜调节像距结构示意图[23]

前面已提到,数值孔径对光谱检测具有较大影响,其主要表现为：当数值孔径较大时,光栅衍射所生成的像也较大,此时像的弯曲和畸变表现得更为明显。针对该问题,一种通过添加平凸厚透镜的方案被提出,这就是人们熟知的Dyson光谱仪,如图9所示[24]。图中,平凸厚透镜与光栅的圆心重合,且透镜的中心轴与光栅法线也重合。狭缝紧贴于透镜后表面,当光束从狭缝入射时,由于光栅衍射和透镜凸面的折射,最终汇聚在透镜后表面上成像。将探测器的敏感面置于像面上,此时像可在探测器上被检测。为校正谱线弯曲和色畸变,推导出光栅和透镜的曲率半径(R和r)须满足条件R/r=n/(n-1)(其中n为透镜的折射率)。进一步,选取曲率半径分别为135 mm、69 mm的光栅和透镜,制作了一台数值孔径为0.66的样机系统,结果表明,在3650 nm、3655 nm和3663 nm处,谱线弯曲和色畸变几乎为0。

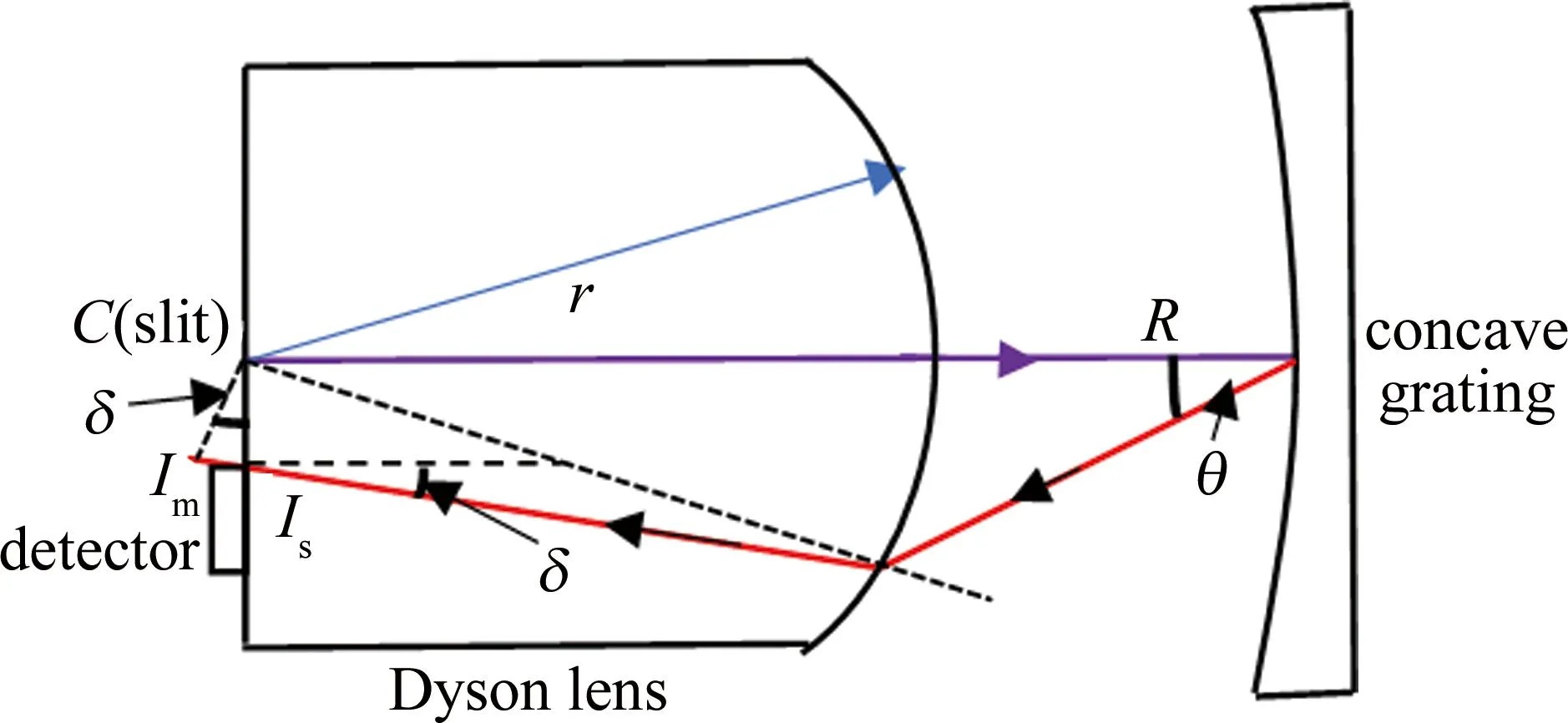
图9 Dyson结构任意光线下子午面与弧矢面成像示意图[24]

然而,该光谱仪只适用于衍射角较小的情况。当衍射角增大时,由于不同波长的子午焦距不同,谱线弯曲、色畸变以及像散仍存在。为此,MONTERO-ORILLE等人[25]在图9的基础上,提出了一种在双波长下校正谱线弯曲、色畸变的方法。其原理是：在衍射角θ为任意角度的情况下,选取合适的临界波长λa和λb,运用正弦定理和斯涅耳定律对R/r进行修正,当δ=0°(δ为子午像点于平凸厚透镜后表面法线的夹角)时,谱线弯曲、色畸变以及像散均得到较好校正。理论分析表明,当临界波长分别为400 nm和1000 nm、光栅曲率半径为179.86 mm、透镜半径为59.25 mm时,像高谱线弯曲为0.007 μm,色畸变为0.026 μm。

图9中,由于探测器具有一定尺寸、无法与透镜后表面完全贴合,会导致探测器无法检测到成像,从而不利于其安装、使用。针对该情况,一种利用全反射面折叠光路的方案被提出[26],如图10所示。图中,将平凸厚透镜替换为一面带有反射镜的特殊透镜,其作用是将原本汇聚在后表面的光束、在透镜焦距不变的情况下,反射并汇聚到透镜外的像面上。理论分析表明,在光谱范围为350 nm～1050 nm、光栅曲率半径为165 mm、透镜凸面曲率半径为53.693 mm、全反射临界角为50°的情况下,像面和透镜之间达到1 mm的分离,谱线弯曲为0.05 μm,色畸变为0.7 μm。此外,当使用一块2次曲面系数为-0.9076的非球面光栅替代球面光栅时,焦平面与厚透镜后表面之间高达7 mm的分离,可进一步满足探测器的安装使用[27]。同时,光斑的均方根半径从24 μm减小到6 μm。图中,TIR(total internal reflection)为全内反射透镜。

虽然上述设计确保了探测器的检测使用,但由于其带有全反射面的特殊透镜的厚度较大,会导致系统的杂散光较大。为此,参考文献[28]中将图10所示带有全反射面的透镜替换成较薄的平凸厚透镜,并提出了一种非球面校正镜设计思路,如图11所示。图中,让平行光束通过由ZnSe和Ge材料制成的透镜组合,将该光束聚焦至透镜外,确保了探测器安装使用。非球面镜的添加,提供了一个非球面系数,校正了由减小透镜厚度带来的球差问题。此外,可通过旋转像面,将各波长下、原本不在同一垂面上的最小弥散光斑置于同一平面上,平衡了色差,从而使得每个波长的光束都能理想成像。理论分析表明,在波长范围为7.5 μm～10 μm时,系统的杂散光减小到10-7量级,谱线弯曲小于4.051 μm,色畸变小于4.154 μm,说明该设计思路是可行的。图中,FPA(focal plane array)为焦平面阵列。

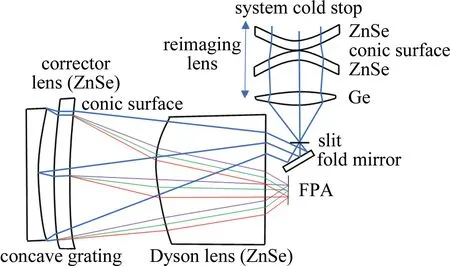
图11 非球面镜法结构示意图[28]

2 提高分辨率的研究进展

除像差外,分辨率也是影响光谱检测精度的另一个重要影响因素。总结当前研究成果,可将提高分辨率的方法概括为窄波段分割以及宽波段分割两种类型。

2.1 窄波段分辨率提升的研究进展

光谱分辨率由色散器件角色散本领、会聚透镜的焦距以及探测器像元尺寸共同决定[29]。若系统色散能力越大,则像的分辨率越高[30]。对于窄波段来说,提高分辨率的做法是：通过改进光栅架构、或添加辅助元器件来提升整个检测波段的色散率。

基于该思路,参考文献[31]中提出了一种改进光栅架构提高分辨率的方案。该方案依据色散率和分辨率的关系,在考虑光程和入射光束波长的情况下,采用牛顿迭代法,从光栅顶点开始,依次确定刻槽位置和闪耀角,从而提高分辨率。以此为基础,研究者们还对非罗兰圆、线性色散、以及多级衍射类型的光栅分辨率进行了分析,结果表明：以牛顿迭代算法制作的光栅均可提升分辨率。

牛顿迭代法虽能从高分辨率角度、合理地布局光栅刻线的排列,但其大量的迭代次数,使得求解刻线位置的时间较长。针对该问题,参考文献[32]中提出了一种简易、高分辨率的光栅设计方法。其步骤为：首先运用光程函数,建立光栅架构非线性优化方程,并采用全局搜索算法求解最佳刻线位置;其次,通过微调光源和探测器的位置参数,获取检测范围内可提升色散率的色散距离。分析结果表明,在狭缝宽度为50 μm、波长范围为370 nm～780 nm、入射距离为120 mm、像面距离为124.5 mm的情况下,像的最小分辨率可达2 nm,而最高分辨率达到0.8 nm以上。

实际应用中,由于检测室内部背景等杂散光的存在,必然导致分辨率下降。针对该情况,REN等人[33-34]提出了一种检测室内壁刻槽提升分辨率的方案,并搭建出如图12所示的检测系统。图中,由于杂散光在凹槽处发生多次反射直至光能完全衰减,则可避免探测器上同一处出现多波长光束同时介入的情况,从而分辨率得到了提高。结果表明,在波长范围为400 nm～1000 nm、内壁刻槽深度和宽度分别为1 cm和2 cm时,分辨率可达1.4 nm。

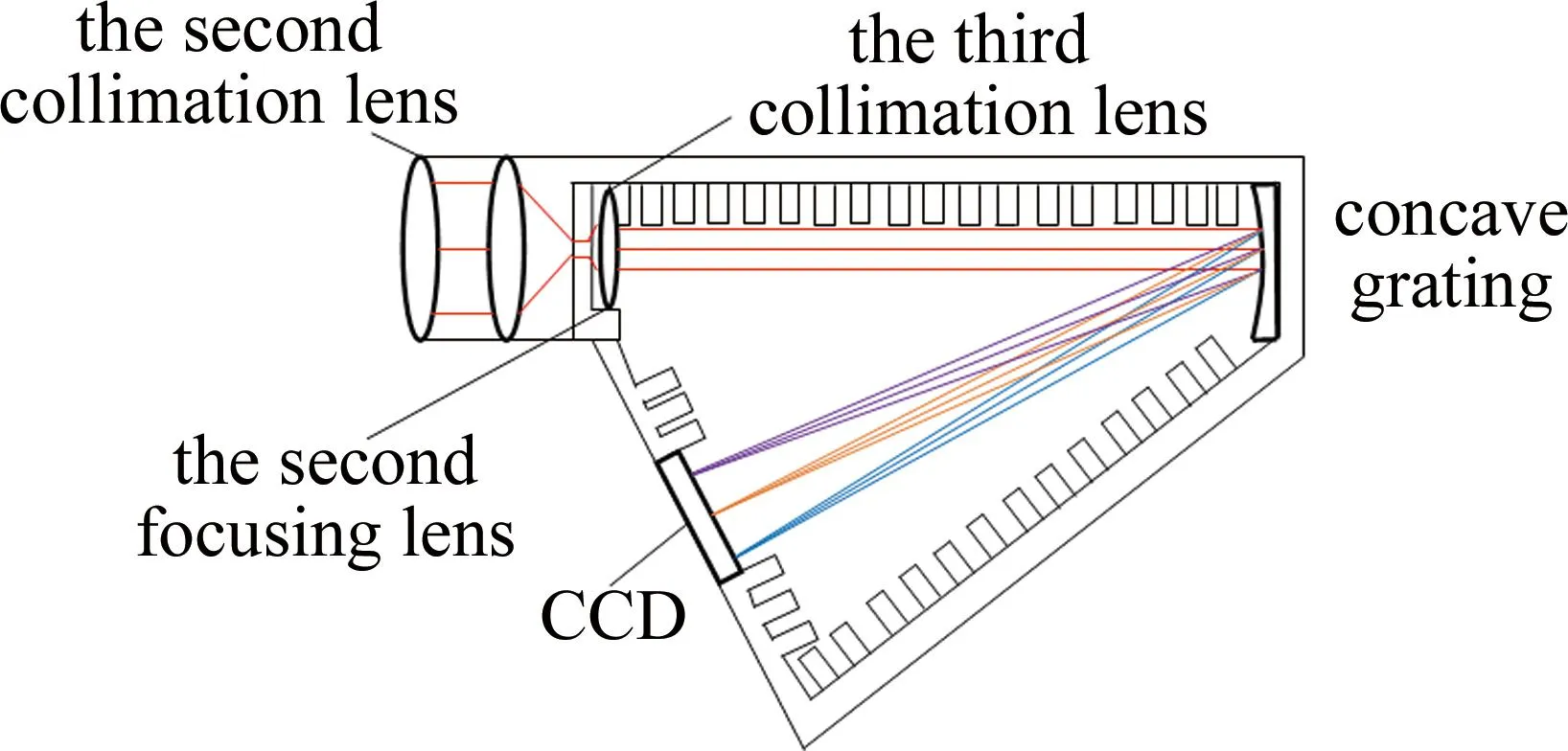
图12 内壁刻槽结构示意图[33]

为进一步提高窄波段内的分辨率,CAO等人[35]提出了一种双光栅色散叠加的方案,如图13所示。图中,将两块参数完全相同的光栅固定在同一光栅座上,通过波长扫描结构驱动光栅同轴旋转。不同波长的衍射光束对应相应的转角,在不同转角处,探测器接收到不同波长的光,由此可实现连续波长范围内的光谱检测。由于两块光栅的共同使用,将系统色散能力提高为原来的两倍,从而进一步提高了分辨率。结果表明,在波长为170 nm～380 nm的范围内,分辨率可达0.8 nm。

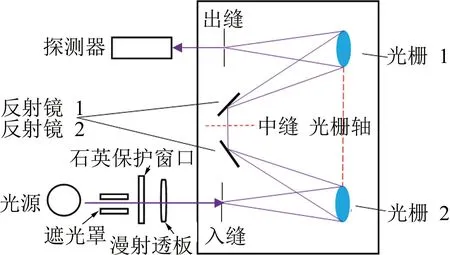
图13 双光栅色散叠加结构[35]

上述方案虽能有效提高窄波段内的分辨率,但成像呈曲面形状,与平面探测器相匹配时,会导致检测精度的下降。为此,LI等人[36]提出了透镜提高色散能力的方案,如图14所示。图中,将第2块光栅替换为2块透镜的组合。透镜的作用是将原本不易检测曲面像谱变换为平面像谱。同时,增大了色散距离,从而提高了系统的线性色散。结果表明,在波长为320 nm～800 nm范围内,两块透镜焦距分别选择为80 mm、60.1 mm,分辨率可达0.5 nm,较前一方案相比分辨率得到显著提升。此外,在特定波长处添加一块条形滤光片,可进一步提高检测精度。

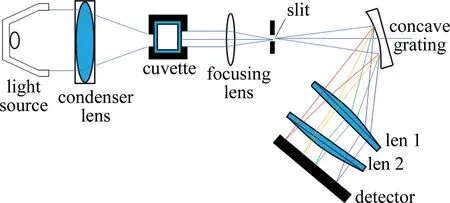
图14 透镜优化色散结构示意图[36]

2.2 宽波段分辨率提升的研究进展

上述方法虽能有效地提高窄波段分辨率,但由于色散距离限制,当谱宽较大时,高分辨率的检测效果难以实现[37]。针对该问题,一种对频带分割的方法被提出。其做法为：在确保探测器长度较短的情况,依据谱宽与分辨率的关系,利用光栅或不同辅助元器件将宽波段分割为若干窄波段依次检测。参考文献[38]中利用该方法设计了一种利用3块光栅切换、分割波段的检测结构,如图15所示。图中,O1、O2、O3为光栅中心,将波段为400 nm～2500 nm光源发出的光束通过旋转光栅分割为400 nm～1000 nm、1000 nm～1700 nm和1700 nm～2500 nm 3个子波段,并利用上述窄波段提高分辨率的方法对每个波段进行改善后,再进行检测。结果表明,以上3个波段的分辨率分别为2.5 nm、4.3 nm、6.2 nm,较好满足了近、中红外光检测需求。

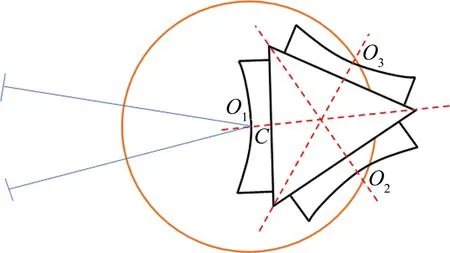
图15 3块光栅分割波段结构示意图[38]

上述方案虽然可实现高分辨率的宽带检测,多块光栅运用时,增加了系统的复杂性。针对该问题,一种双缝入射方案被提出[39],如图16所示。图中,将其中两块光栅替换为两个入射狭缝,在满足等衍射角的条件下,运用光栅方程和光程函数确定入射角和狭缝位置,使用狭缝A1、A2将λ1-λ3波段分割为2个子波段。当光束在A1狭缝处入射时,可将λ1-λ2的光束投影到探测器上;同理在A2狭缝处入射时,可将λ2-λ3的光束投影到探测器上。这里的λ1-λ3表示检测总带宽,λ1-λ2和λ2-λ3为被分割成的两个较窄的子带宽。实验结果表明,在400 nm～1200 nm波段内,系统分辨率可达1.8 nm。进一步,ZHOU等人[40]在图16的基础上,将其中的一个狭缝替换为一块反射镜,设计了一种反射镜灵活的分割波段改进结构。当入射光线不经过反射镜时,在探测器上可接收λ1-λ2波段的光谱;当反射镜向下移动至合适位置时,可接收λ2-λ3波段的光谱。需要强调的是,该反射镜是一种只反射500 nm以上光束的特殊反射镜。由于该镜的使用,在分辨率不减的同时让波段分割变得更为灵活。结果表明,在将工作波段200 nm～900 nm分割成200 nm～550 nm和550 nm～900 nm的情况下,系统分辨率可达1.2 nm。

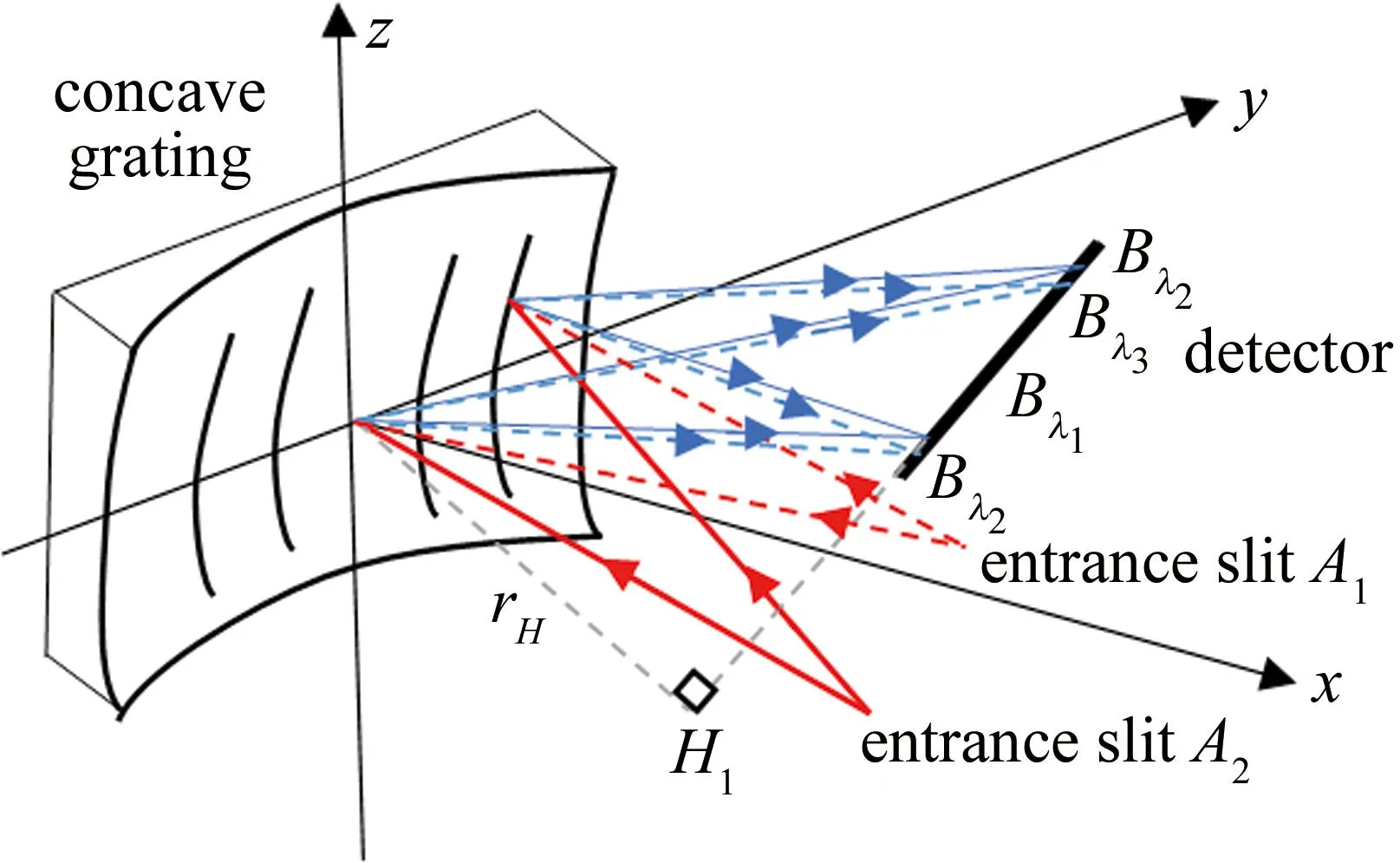
图16 双缝输入方案结构示意图[39]

为进一步提高宽波段的分辨率,LU等人[41]在利用反射镜高灵活度的优势、并考虑系统色散能力和复杂性的情况下,设计出一种双光栅分割波段的结构,如图17所示。图中,将两块完全相同且刻线密度为2400 line/mm的光栅和信号接收装置于同一罗兰圆上。依据上述检测原理,通过适当调节光束的入射角度和反射镜的位置,使得所设计的整个波段信号能被接收装置采集。由于刻线密度的增大,提升了光栅的角色散能力,从而使得分辨率得到提高。结果表明,当波长范围为200 nm～700 nm、入射角为60°时,系统的分辨率达0.4 nm。

3 结束语

针对光谱检测对高质量图像的要求,从消像差和提高分辨率两方面入手,综述了提高成像质量的最新进展。对于消像差,将其归纳为单光栅和添加辅助元器件两种方案;对于提高分辨率,将其归纳为窄带以及宽波段分割两种方案。在此基础上,对不同方案的优势进行了分析,归类了这些方案采用的设计技巧,总结了所取得的阶段性成果。通过分析不难发现,对于消像差,单光栅方案虽能有效校正像差,但频带范围较大时,每个波长处像差仍难以消除,需要通过添加辅助元器件加以改善;而对于提升分辨率,窄带检测方法虽对分辨率的提升行之有效,但色散距离限制对宽波段分辨率的影响不容忽视,需通过分割波段予以改进。针对上述问题,未来可在选取低像差光栅的基础上,通过级联多块线密度较低的光栅或减小透镜厚度等办法进一步实现对像差的校正;通过增加元器件数量将波段分割得更为精细,在检测波段更宽、体积较小的情况下,进一步获取更高分辨率。相信在不久的将来,基于凹面光栅的高质量光谱检测将能得到更快的发展,实现更为广泛的应用。