多基色激光显示系统彩色散斑分布特性的研究

邓林宵,杨雨桦,姚昞晖,朱立全,王 贯,顾 春,许立新*

(1.中国科学技术大学 核探测与核电子学国家重点实验室,合肥 230026;2.中国科学技术大学 物理学院 安徽省光电子科学与技术重点实验室,合肥 230026;3先进激光技术安徽省实验室,合肥 230026)

引 言

激光显示具有亮度高、色域大、使用寿命长等优点[1-3]。目前,激光显示最常见的实现方式是激光投影显示。然而,高相干的激光通过光学粗糙表面的传播会引起散射光的干涉,形成一个随机的光强度分布,即散斑[4-7]。

在激光投影系统中,颜色一般是由红、绿、蓝三基色激光叠加而合成[8]。当纯白色图像均匀照射在屏幕上时,由于红绿蓝激光器产生的散斑图案不相关,人们将观察到随机分布的彩色颗粒噪声,即彩色散斑。彩色散斑理论最早由KURODA等人[9]提出,含有彩色散斑的图像质量将严重下降。因此,在激光显示走向产业化的前沿,有必要对彩色散斑进行研究和评价。

目前关于彩色散斑的研究还比较少,主要来源于国际标准IEC 62906-5-4[10]及其相关文献[11-12]。然而其相关参数沿用了色品图的坐标轴变量(如xy或u′v′等),不能直观地反映彩色散斑与颜色的关系,且对特定方向的方差计算比较复杂,过多的变量导致不同投影机之间彩色散斑的比较不够直观。此外,这些文献中通常基于三基色显示系统,而为了尽可能地提升显示色域,多基色激光显示是未来重要的发展方向[13],但目前研究多基色激光显示的彩色散斑特性的文献报道很少。

本文作者依据现有的国际标准,推导了多基色显示的彩色散斑分布,并在国际照明委员会(Commission Internationale de l’Eclairage,CIE)发布的CIE-u′v′色品图中,通过拟合彩色散斑散点,定义了彩色散斑椭圆的简化模型来直观地描述显示系统的彩色散斑特性;通过改变随机数的分布,研究了彩色散斑分布与散斑对比度的关系;通过改变基色数目,研究了3～6个基色的激光显示系统彩色散斑分布的变化;通过改变波长组合,研究了不同基色波长对彩色散斑的影响。这些研究结果可作为未来标准化彩色散斑评估的依据。

1 多基色彩色散斑分布的理论推导

根据IEC 62906-5-4文件,计算红绿蓝三基色系统白平衡点的XYZ三刺激值时,可写为基于辐射度量的形式：

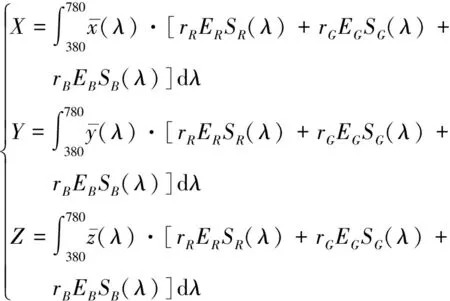
(1)

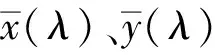
若将(1)式推广到含有m个基色的系统(m≥3),将得到：

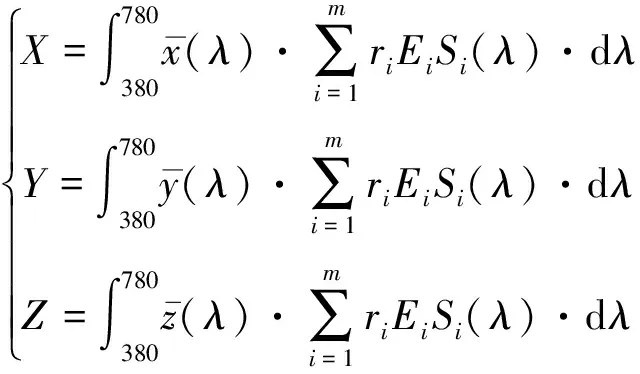
(2)

式中,i=1,2,…,m代表第i个基色。

当每个基色完全不相干、Ei均取为1时,可得到m个基色系统的白点坐标,此时纯白色图像的空间中n个取样像素点是均匀的白色;当相干噪声存在,该n个点的各基色光照度满足特定分布,此时白色图像中存在彩色的颗粒斑点,则所述空间中各基色的照度分布可写为：

E11,E12,…,E1n;E21,E22,…,E2n;…;

Em1,Em2,…,Emn

(3)

因此,含有彩色散斑的白色图像中某一点的三刺激值由下式给出：

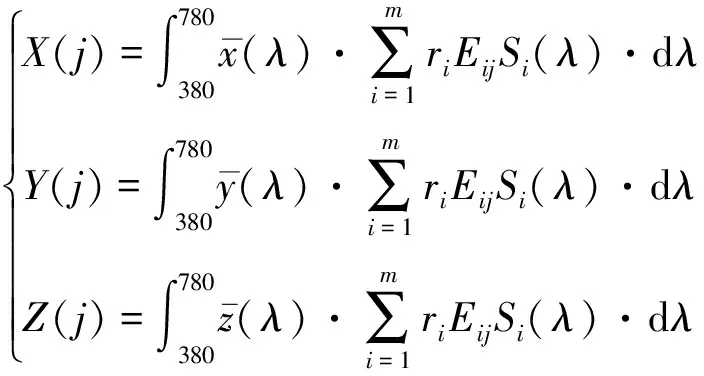
(4)

式中,j=1,2,…,n。

若已知多基色系统光源的光谱分布Si(λ)、各基色权重配比ri,再用参考文献[15]中相似的蒙特卡洛方法进行彩色散斑模拟,则各基色的相对照度分布由下式计算：

EN=Γ-1(W,α,β)/α

(5)

式中,N=λ1,λ2,…,λm(m≥3),当m=3时,λ1,λ2,λ3对应R,G,B三基色,Γ-1代表Microsoft Excel中伽马分布累积分布函数的反函数,W代表[0,1]区间内的随机数,α代表形状参数,β代表尺度参数(β=1),1/α代表归一化。而α=C-2与单色散斑对比度C有关,由下式决定：

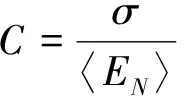
(6)

式中,〈EN〉为单色散斑分布的平均照度,σ为标准差,随机数总数n=10000。由单色散斑对比度C可以计算出光照度分布的(3)式,而(5)式中相应的α=C-2和C均由对应的λ基色计算,最终得到多基色的彩色散斑分布三刺激值的(4)式。根据CIE-xy色品图和CIE-u′v′色品图的定义,用(7)式、(8)式求出相应的色坐标,可将彩色散斑分布画在CIE-u′v′色品图里。

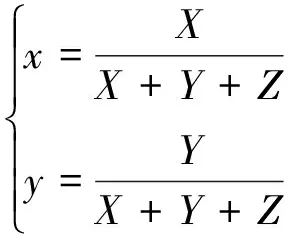
(7)

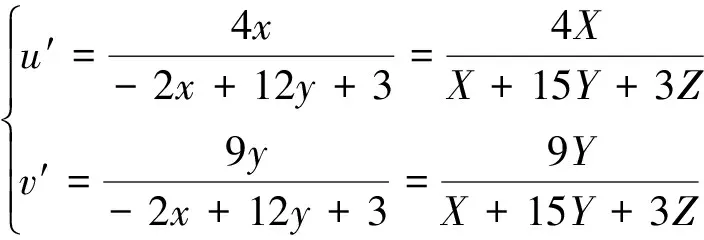
(8)

2 多基色彩色散斑分布的模拟结果

以四基色系统为例,光源的中心波长选为638 nm,550 nm,520 nm,445 nm,这些波长在常见的半导体激光器中都能找到。为了便于分析,将它们的光谱分布简化为高斯型,假设谱宽均为2 nm。应用上一节中讨论的蒙特卡洛方法和(4)式,考虑每个基色的单色散斑对比度都相同的对称情况。结果如图1所示,横纵坐标均为色度学物理量,无单位。舌形区域代表人眼可见的所有颜色,四边形的4个顶点对应于四基色光源的色坐标,围成的区域是四基色系统的显示色域,其内部的红点是系统的白平衡点,本文中设为D65[16](0.3127,0.3290),四边形内散落的黑点代表纯白色图像的彩色散斑分布。

图1 不同基色散斑对比度的四基色系统在色品图中的彩色散斑分布

当散斑对比度C=100%时,如图1a所示,四边形区域内布满了随机分布的黑点,绿色区域的点密度较大,这是因为CIE-u′v′空间在定义的时候,特别缩小了绿色部分的色域面积占比。当C=50%时,如图1b所示,黑点区域的面积变小,整体以白点为中心而缩小。当C=25%时,如图1c所示,黑点区域进一步缩小,其形状也变成近似椭圆形。当C=10%时,如图1d所示,黑点区域整体呈现为一个小椭圆。当C继续减小,到接近0%时,所有黑点逐渐集中在白点上,在这种情况下,彩色散斑“消失”了,整幅图像变成了均匀的白色。

在实际显示系统中,已引入多重的散斑抑制方法,因此最终图像的散斑对比度一般较小。虽然在数值上,散斑对比度40%比60%好很多,但是对于人眼来说,这样的显示图像都不太理想。事实上,散斑对比度在10%以内,甚至接近人眼感知散斑阈值[5, 17](4%或5%)的情况才是商用激光投影机所追求的,消费者通常只需要判断该投影机是否“没有散斑”。因此,本文中所有近似与讨论都假设满足在实际系统中散斑对比度比较小的情况。在C<25%时,也就是对应的α>16时,这一条件满足中心极限定理的近似,此时单一基色的照度分布由原来的伽马分布趋近于高斯分布。如果对整个散点区域的边界作一个近似,相当于把从白点出发沿各个颜色方向的彩色散斑最大色差点作一个包络,将得到一个椭圆形。这个简化的模型可以直观地表现彩色散斑的分布区域与严重程度。因此,本文作者用相关软件中非线性拟合函数来计算彩色散斑特征椭圆,并定义彩色散斑特征量。其中,椭圆半长轴A代表彩色散斑最严重的色差大小,其与u′轴正方向按逆时针方向旋转的夹角H代表彩色散斑最严重的颜色方向,该特征量和色调有关,椭圆面积S代表空间取样点整体的彩色散斑严重程度。如图2所示,随着散斑对比度的增加,椭圆半长轴A和椭圆面积S均增大。半长轴A和散斑对比度C有良好的线性关系,而椭圆面积S随散斑对比度C增加的速率更快,这可能是由于面积与半长轴大致是平方关系。于是,图2a中函数关系近似为直线,图2b中则接近二次幂函数曲线。图中,A、S均无单位。

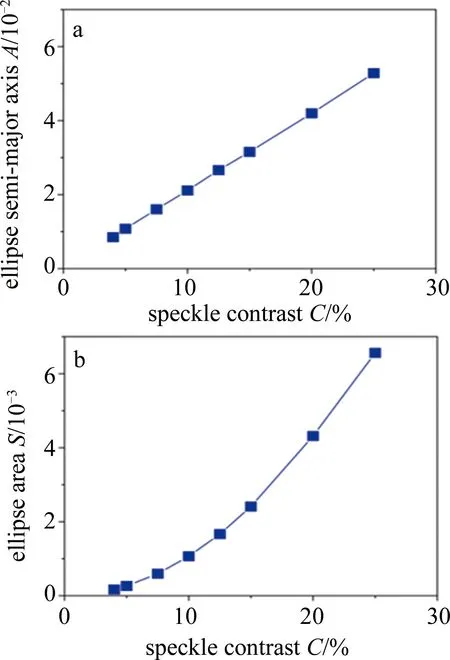
图2 不同基色散斑对比度的四基色系统的彩色散斑特征量

定义了彩色散斑特征量后,便可以计算出不同基色数目的多基色系统的彩色散斑分布。画出了3～6个基色系统在CIE-u′v′色品图中的彩色散斑分布,如图3所示。其中,所有的基色波长均在660 nm,638 nm,550 nm,520 nm,465 nm,445 nm中选取,所有系统中每个基色的散斑对比度C均设为10%。可以看到,随着基色数目的增加,彩色散斑椭圆明显减小。在表1中给出了彩色散斑特征量的具体数值,由角度H可知,色品图中绿色是所有基色中色差最大的方向,也就是彩色散斑最严重的方向,说明绿色对彩色散斑的影响最大。此外,随着基色数目的增加,椭圆半长轴、面积都减小,其中五基色的半长轴略有不符,这可能是基色的波长组合差异造成的。

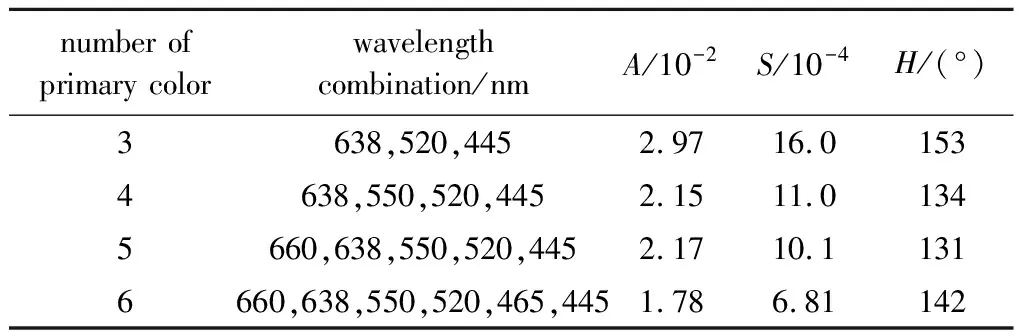
表1 不同基色数目的激光显示系统的彩色散斑特征量

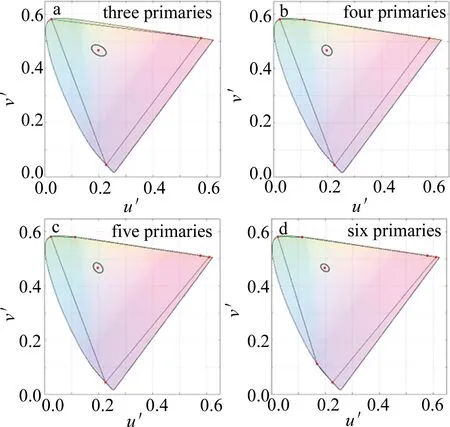
图3 不同基色数目的多基色系统在色品图中的彩色散斑分布(C=10%)

为了探究不同基色组合对彩色散斑分布的影响,改变了基色的波长组合,每个基色的散斑对比度仍然设为10%,结果如图4所示。在采用的3～5个基色的波长组合中,去掉了520 nm的绿基色,只保留550 nm,如表2所示。与图3对比可知,对于相同基色数目的系统,只含550 nm绿基色的组合,其椭圆半长轴和面积均小于含有520 nm绿基色的组合,对应图4中椭圆区域更小,彩色散斑现象更轻微。另一方面,只含550 nm的组合的彩色散斑角度H在110°～120°范围,其方向与舌形边缘光谱轨迹上550 nm的单色光相对应,而含有520 nm的组合其角度H在130°～150°范围内,其方向朝光谱轨迹上520 nm单色光偏转。

表2 不同基色组合的激光显示系统的彩色散斑特征量

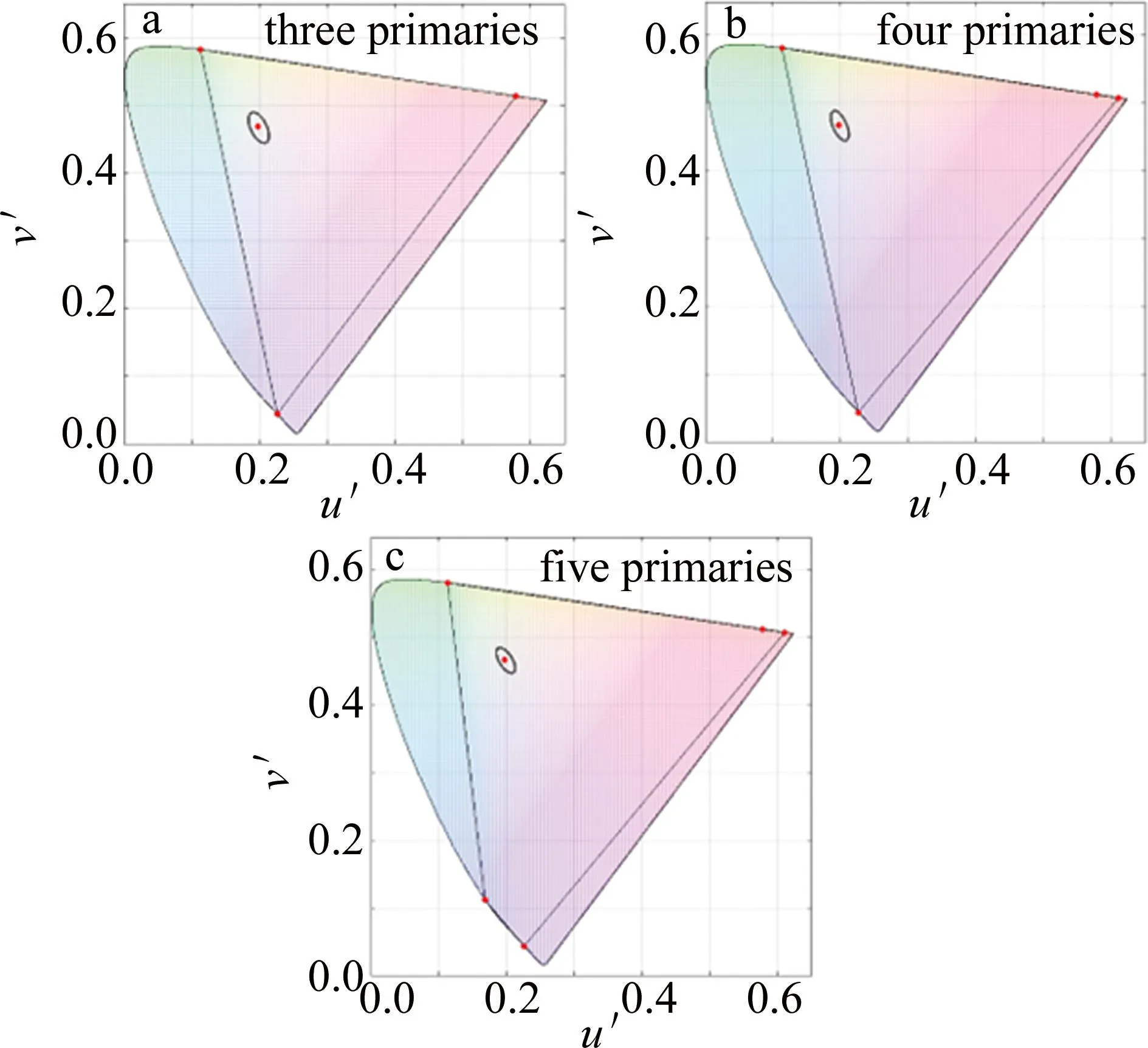
图4 不同基色波长组合的多基色系统在色品图中的彩色散斑分布

在实际显示系统中,不同基色的单色散斑对比度往往不同,因此上述讨论的对称情况并不能反映实际系统。在这里,考虑一个较夸张的非对称情况,四基色的波长组合仍是638 nm,550 nm,520 nm,445 nm,但散斑对比度满足C为5%,5%,25%,5%,其中520 nm基色的散斑对比度远大于其它3个基色。如图5a所示,由于520 nm单色的散斑对比度最大,彩色散斑椭圆将沿着520 nm的绿色方向延伸。

图5 不同基色亮度配比的四基色系统在色品图中的彩色散斑分布

除了基色数目和基色组合,上述在多基色系统中的讨论中还忽略了一点：基色的亮度配比。当给定白平衡点时,三基色系统的亮度配比有唯一解,而四基色系统增加了一个配平的自由度,更多基色的系统将有更多的配平自由度[18]。因此,当四基色系统的亮度配比调整时,如果降低绿色中550 nm基色的权重,而相应增加520 nm基色的权重,彩色散斑椭圆将明显增大,如图5b所示,说明调整配比后系统的彩色散斑变严重。相反的,如果适当地减小520 nm基色的权重,彩色散斑现象将有所减轻。表3中给出了两种配比的彩色散斑特征量值,当520 nm基色的权重增加时,角度H基本不变,椭圆半长轴、面积均增大。这说明,在多基色显示系统中,如果某个基色的散斑现象比较严重,可以在求解多基色的白平衡点亮度配平时尽量让其占比减小,那么在同样的白点下,整个系统的散斑可以得到(有限的)减小。然而,这种方式如果过多地降低某一基色亮度,会带来总的3维立体色域[19]的减小,这一点在平面色品图中是不易察觉的。因此,就像基于光谱展宽的散斑抑制方式会导致颜色饱和度下降一样,有时颜色的表现和散斑的抑制是一个权衡。

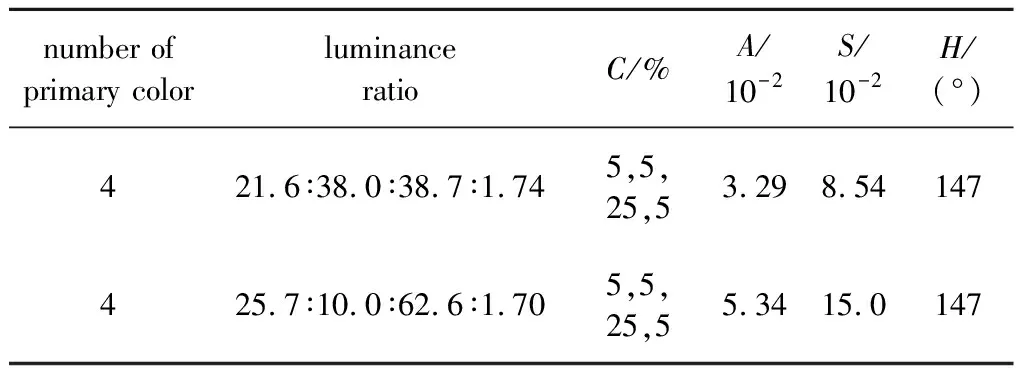
表3 不同基色亮度配比的四基色激光显示系统的彩色散斑特征量

此外,本文中的讨论也存在一定的局限性。首先,单色散斑分布假设完全服从伽马分布,并没有考虑具体屏幕结构[20]或观测距离[5]等对散斑对比度的影响,如果要在实验上研究基色数目和波长组合等对散斑的影响,需要严格控制变量;其次,在CIE-u′v′均匀色品图中,颜色的感知也并不是完全均匀的,不同方向颜色感知的差异导致其色差难以比较,理想情况下,均匀色品图里颜色的感知分辨应该是一个圆,即各个方向的感知分辨色差相等,此时使用简化的彩色散斑椭圆区域和人眼分辨圆相比较,可以更准确地判断彩色散斑的感知。如果要考虑亮度对颜色的影响,那么使用3维颜色空间会比平面色品图更好[21],但目前最广泛使用的CIELAB空间[14]有归一化亮度限制,并不适合用来描述彩色散斑[22],而其它更均匀的颜色空间[23]还有待进一步研究。

3 结 论

研究了多基色激光显示系统的彩色散斑特性,将已有的三基色彩色散斑理论推广至多基色系统。在CIE-u′v′色品图中,考虑散斑对比度小于25%的实际系统情况,定义了彩色散斑椭圆的简化模型来直观地描述显示系统的彩色散斑特性,其中包括椭圆半长轴、方向角以及面积3个参数,对应彩色散斑散点区域分布的特征。椭圆半长轴的长度代表彩色散斑的最大色差;方向角代表彩色散斑最严重的方向;椭圆面积代表彩色散斑的严重程度。模拟结果表明,随着基色数目增加,椭圆面积减小,彩色散斑严重程度减轻;三基色系统的椭圆面积为16.0×10-4,而六基色系统的椭圆面积为6.81×10-4。进一步分析基色不同波长组合对彩色散斑的影响,发现绿色对彩色散斑的影响最大。在多基色显示系统中,当白平衡点不变时,如果减小散斑对比度较大的基色的亮度权重,彩色散斑椭圆将变小,彩色散斑现象将减弱。本文中的研究可为多基色激光显示系统的彩色散斑评估提供理论指导。在未来,如果有更均匀的颜色平面或者颜色空间,该方法的简化模型可以更精确地描述彩色散斑。