新型电容式传感器的设计与优化*
史兆强, 李 明
(河南工学院 电子信息工程学院,河南 新乡 453003)
0 引 言
广阔无边的海洋世界拥有多种丰富的能源和原材料,是人类陆地资源外的另一块存储宝库[1]。众所周知,海洋环境复杂,当遇到混浊海水时,光在传输过程中会受到混浊介质的严重散射,限制了光学探测的距离以及水下光学成像探测的应用。由于超声波具有极强的定向功能,穿透性较好,声强较大,使其易于将声能集中传播,具有较远的探测范围,因此,超声波在水下得到了广泛应用[2]。
超声波换能器是整个水下超声成像系统最重要的部件,制约着整个水下成像检测技术的发展。目前,国外已经开展利用微机电系统(MEMS)技术制作电容式换能器集成成像面阵的研究,用以提高超声波换能器阵列灵敏度和一致性[3,4],然而,国内却还是集中在利用分立压电陶瓷水听器组装成成像面阵技术的研究上,只有极少单位进行了利用MEMS微加工技术制作集成成像面阵的研究,并且MEMS微加工技术研制超声成像系统方面尚没有理想的试验结果[5,6]。总体来说,国内对水声成像技术的研究相对于国外较滞后,缺乏具有完全自主知识产权的水声成像声纳产品,尤其在MEMS超声成像研究方面基本是空白。
鉴于以上分析,本文提出了一种Simulink构建的微电容式超声波换能器(capacitive micromachined ultrasonic transducer,CMUT)敏感单元动态系统,通过模拟仿真对CMUT敏感单元进行发射/接收特性分析,分析了CMUT敏感单元在水下环境中的塌陷现象、不同发射情况下其位移、声压特性。同时对CMUT接收模式下薄膜的平均位移及产生的微小电流进行了仿真分析。
1 CMUT基本结构与工作原理
CMUT阵列属于多层复合结构,如图1(a)所示,阵列由多组阵元(element)规则排列构成,单个阵元又由较多个最基础元素敏感单元(cell)并行规则排列组成。从图1(b)中可以看出,CMUT敏感单元结构的上电极进行了图形化处理,振动薄膜也被刻蚀了隔离槽,该图通过对上、下电极正对面积的缩减,从而减小CMUT的寄生电容。

图1 CMUT阵列结构示意
CMUT工作原理如图2所示,可以看出,CMUT工作在发射模式和接收模式都存在直流(DC)偏置电压施加在敏感单元上下电极[7],直流偏置电压产生的静电力将敏感单元振动薄膜拉向极板下端,但由于薄膜自身存在反向的回复力,使得薄膜很快静止达到平衡状态。若在此刻对薄膜再次施加一定频率的交流(AC)激励电压,便会使振动薄膜发生挠曲,辐射相应频率的超声波;若在平衡状态下,薄膜受到声压变化引起挠曲,进而极板间电容变化产生微弱的电流信号,后经跨阻放大等处理电路实现电压信号接收。
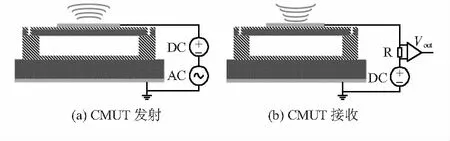
图2 CMUT的工作原理
2 CMUT敏感单元理论分析与建模
2.1 CMUT敏感单元薄板振动理论分析
CMUT敏感单元可看作圆形薄板,以薄板圆心为坐标原点,且将平面内质点的振动看作垂直方向的上下运动,依据板壳理论,当CMUT薄膜承受均匀分布力作用时,振动位移的微分方程[8,9]表示
(1)
式中h,σ,E,ρ和w分别为薄膜的厚度、材料泊松比、杨氏模量、材料密度和位移;T和p分别为薄膜的内应力、外部作用的压力。求解式(1)得
(2)
式中a为可动上极板半径,J0(x)和I0(x)分别为第一类零阶贝塞尔函数和第一类零阶修正贝塞尔函数,J1(x)和I1(x)分别为第一类一阶贝塞尔函数和第一类一阶修正贝塞尔函数。
假如把薄板看成如矩形、圆形等规则形状,可近似给出谐振频率的表达式。对于边缘固定支撑且半径为a、厚度为tm的圆形薄板,其在空气(真空)和液体中的固有频率表达式[10]如式(3)所示
(3)
其中,ρl为液体介质的密度。
薄膜最大位移直接影响着CMUT敏感单元的发射性能,薄膜移动越大,做功越大,发射出的声压也会相应增大。谐振频率作为换能器性能的一个重要指标,直接影响着其使用频带范围、探测范围等。结合式(2)和式(3),利用MATLAB分别获得CMUT薄膜的振动位移/频率与其尺寸(半径、厚度)的变化情况,如图3。其中,CMUT薄膜材料为硅,杨氏模量E=169 GPa,泊松比σ=0.29,密度ρ=2 332 kg/m3,内部张力T=20 MPa,外部压力p=1 Pa。图3(a)给出了薄膜在50~100 μm,厚度为2~3 μm范围内最大位移为1 μm。可看出,薄膜半径的增大或膜厚度的减小都会使振动位移增大,且经过对比,半径对位移的影响更大。同理可看出,薄膜半径的减小或膜厚度的增大都会使谐振频率增大,且经过对比,厚度对频率的影响更大。
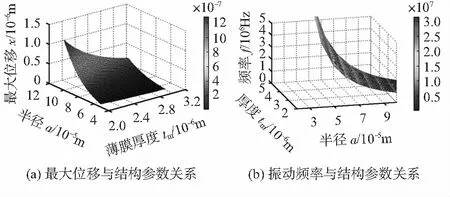
图3 薄膜振动位移/频率与结构参数关系
2.2 CMUT敏感单元平行板电容模型
将CMUT简化为下电极固定、上电极可垂直移动的平行板电容器模型。当CMUT受到静电力作用时,上电极下拉接近下电极,为了达到平衡会产生回复力。若将敏感单元的薄膜近似认为是一个质量为meq的质量块,其自身的方向回复力则可近似认为是一个弹性系数为keq的弹簧,薄膜振动过程中的能量损耗简化为一个阻尼元件,初始状态时的极板间距为g0。
假设敏感单元薄膜位移变化为w,由牛顿第二定律可知,其所受力为
∑F=Fe+Fs+Fb=ma=md2w(t)/dt2
(4)
式中Fs为回复力,Fb为阻尼力,Fe为将上电极下拉的静电力。
从CMUT平板电容模型看出,当CMUT的静电力大于回复力时,薄膜会出现塌陷情况,在应用中,为了提高敏感单元机电转换比、灵敏度和发射响应等性能,上、下电极间施加的DC值应小于且最大化靠近塌陷电压。图4为Vcollapse与薄膜结构参数的关系,分析可知薄膜半径减小或腔高增加都会使Vcollapse变大。

图4 塌陷电压与薄膜结构参数的关系
2.3 CMUT敏感单元等效电路模型
运用电—机械(力)—声类比方法,得到CMUT敏感单元在发射/接收的类比等效电路,如图5所示。

图5 CMUT敏感单元发射/接收模式下等效电路
根据CMUT工作原理,当敏感单元工作在发射模式时,其施加的总电压V可表示为
V=VDC+VACsinωt
(5)
CMUT接收灵敏度是由其机电转换比n决定,n越高其接收灵敏度越高。从图6中可以看出,机电转换系数与薄膜半径成正比,与真空腔高成反比。
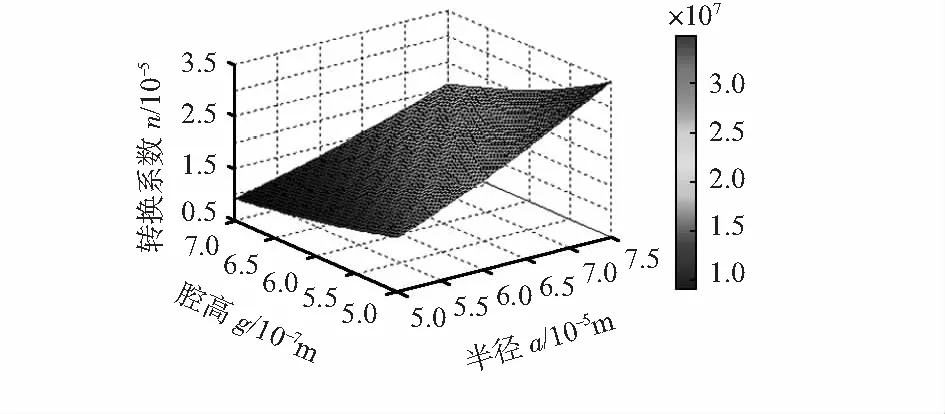
图6 机电转换系数与薄膜主要结构参数的关系
2.4 CMUT敏感单元结构参数确定
工作频率越高目标体成像分辨率越好,但在水中传播时衰减也会越严重,传播距离受限,因此,综合考虑设定CMUT工作频率为400 kHz。当CMUT频率以及薄膜Si材料确定后,便可确定薄膜厚度tm和半径rm的关系。最后综合大气压和水压下最大位移、塌陷电压、机电转换系数要求以及Si-SOI键合工艺条件确定薄膜尺寸。最终器件的结构参数为:上电极半径45 μm,上电极厚度0.2 μm,隔离层厚度0.15 μm,薄膜半径90 μm,薄膜厚度3 μm,空腔高度0.8 μm,绝缘层厚度0.15 μm。
3 CMUT敏感单元Simulink动态性能分析
3.1 发射性能建模、仿真与分析
当CMUT工作在发射模式时,薄膜主要受到大气压力(Fa=PS,P为大气压强)、静电力(Fe)、回复力(Fs)和阻尼力(Fb)的作用,由式(6)表示
(6)
CMUT工作在发射模式时的发射声压定义如下
Pa=Re(Zm)ωA
(7)
式中Zm为介质的阻抗,ω为角频率,A为超声波的振幅,可用薄膜的振幅近似等效。交流激励电压越大,振动薄膜的振幅越大,由式(7)可得,发射声压与薄膜的振幅成正比。因此,发射声压与交流激励电压正相关。
通常,取塌陷电压临界值为薄膜平衡位移下降至真空腔高的1/3 时所承受的VDC值。仅向敏感单元上、下电极施加VDC时薄膜下降位移变化如图7所示。本文设计的真空腔高为0.8 μm,1/3腔高即为0.267 μm。从图7可看出,当薄膜开始受到VDC作用时,会产生一个较大的位移变动,但随着自身回复力的相互作用,薄膜位移会很快稳定,且随着VDC变大,薄膜平衡位移越低。当施加40 V直流偏置电压,位移约0.243 μm,当施加43 V直流偏置电压,薄膜平衡位移约0.257 μm,当输入电压为塌陷电压,即134.13 V时,其最大振动位移约为0.23 μm,即空腔高度0.7 μm的1/3,当施加45 V直流偏置电压时,薄膜平衡位移约0.266 μm,非常接近0.267 μm,故可取45 V作为所设计的CMUT敏感单元的塌陷电压。
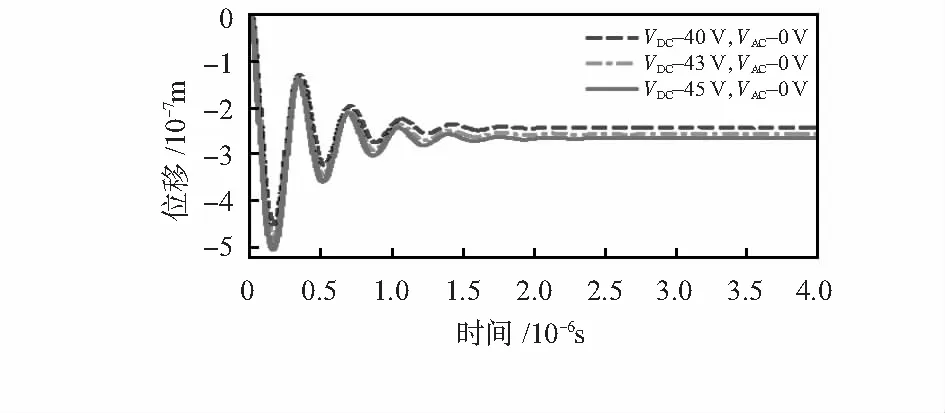
图7 薄膜位移随偏置电压变化情况
薄膜振动位移与辐射声压随直流偏置电压和交流激励电压的变化情况如图8所示。从图8(a)中可看出,薄膜达到稳定状态后,薄膜的位移会出现周期性变化。当向薄膜施加恒为25 V的偏置电压VDC时,改变激励电压VAC的条件(10 V和20 V),可看出随着激励电压VAC增大,薄膜的振动幅度也相应增大。当向薄膜施加恒为25 V的激励电压VAC时,改变偏置电压VDC的条件(10 V和20 V),可看出随着偏置电压VDC增大,薄膜平衡位移越低,同时发现薄膜的振动幅度却在一定程度增大,但与激励电压VAC对薄膜振幅的影响相比,偏置电压VDC产生的影响较小。当VDC=20 V,VAC=25 V时的薄膜振动位移最大。
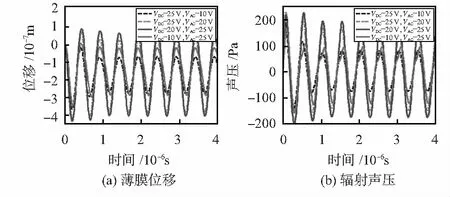
图8 不同发射情况下敏感单元位移、声压特性
CMUT作为发射传感器时,要求CMUT在薄膜未发生塌陷的情况下,尽可能发射较大的声压。CMUT的发射声压与薄膜的振幅成正比。故正如图8(b)所示的4种情况的辐射声压变化一样,VDC=20 V,VAC=25 V时,得到的CMUT发射声压最大。同理,本文在直流偏置和交流激励电压之和限制在塌陷电压以下时,增加了施加电压的变化情况,Simulink仿真分析了不同施加电压下,发射声压变化情况,如图9所示,结果依然还是VDC=20 V,VAC=25 V时,可得到最大的发射声压。

图9 不同激励条件下敏感单元声压特性
3.2 接收性能建模、仿真与分析
CMUT工作在接收模式的Simulink顶层模型主要包括输入(超声波、偏置电压)、输出(薄膜位移和产生的微小电流)和子系统1。
子系统1的功能是实现输入到输出的转换,其主要功能是通过子系统2实现静电力随薄膜位移的变化而变化,通过子系统3实现薄膜位移随静电力、超声波声压的变化而变化,通过子系统4实现电流随薄膜位移的变化而变化。子系统2和子系统3根据静电力式(4)建立和式(6)给出,其中,速度和位移分别是对加速度的一次积分和二次积分建立的,并添加了一个限制位移的模块,可以较好地仿真薄膜塌陷的情况,子系统4根据电流的式(8)建立
(8)
通过固定的16个周期的正弦激励信号表示超声波在介质中传播这一现象。当向薄膜施加45 V偏置电压且受到大气压强和外界声压的共同作用时,用Simulink仿真16个周期的正弦激励信号结果如图10所示。

图10 Simulink仿真结果
从图10可看出,零时刻开始相当于施加一个冲击载荷,薄膜的振动较剧烈,逐渐到达平衡位置做简谐振动。可知Simulink仿真薄膜平衡位移约0.167 3 μm,振幅约0.013 4 μm,产生电流的振幅约8.062 5×10-11。Simulink仿真运算不仅快捷,且有利于提高CMUT结构设计和分析效率。
4 结 论
本文为了能够快速、有效地对CMUT进行特性分析,提出了一种利用Simulink状态模型对CMUT发射/接收性能的动态仿真分析的方法,在Simulink环境中构建CMUT动态系统,针对设计的CMUT敏感单元,利用Simulink模型直接进行系统模拟,分析了CMUT敏感单元在水下环境中的塌陷现象、不同发射情况下其位移、声压特性。同时还仿真分析了CMUT接收模式下薄膜的平均位移及产生的微小电流,验证了该方法具备可行性和高效性,为CMUT结构设计、分析以及测试应用提供了有利的理论依据和参考。

