基于IPSO算法优化GRU神经网络的燃气负荷预测*

海文龙, 王亚慧, 王怀秀

(北京建筑大学 电气与信息工程学院,北京 100044)

0 引 言

安全、稳定的燃气供应对于保证居民正常生产活动极为重要。通过燃气流量传感器采集燃气负荷数据，并对其进行深入研究，进而对未来时段燃气负荷做出预测，可使燃气供应企业提前做好供气预案，以此保障人民正常生活。因此，建立精准的燃气负荷预测模型至关重要。

近年来，许多学者针对负荷预测做了大量研究。由于负荷预测是时间序列预测问题，故一些学者利用擅长处理时序任务的长短期记忆(long short-term memory,LSTM)神经网络模型对其进行预测，该模型可较好解决长期依赖问题[1]。胡向阳等人[2]提出基于多变量LSTM的时间序列预测模型，实验结果表明，该模型性能优于ARIMA模型。虽然LSTM模型有良好的时间序列处理效果，但该模型复杂度高，易出现过拟合情况。同时，训练需要耗费大量时间[3]。门控循环单元(gated recurrent unit,GRU)的提出是对LSTM模型的改进，GRU模型只有2个门控开关，仅用较少的参数即可进行有效预测[4]。但传统GRU模型采用梯度下降法进行参数寻优，不能保证参数是全局最优解[5]。粒子群优化(PSO)算法具有设置参数少、收敛速度快的优点，可较好解决模型参数寻优问题[6]。

本文对PSO算法惯性权重做出改进[7]，提出基于改进PSO(improved PSO,IPSO)的GRU的燃气负荷预测模型。通过IPSO-GRU模型与 LSTM模型、GRU模型的预测结果对比发现，本文所提模型预测效果较好。

1 研究方法

1.1 IPSO

PSO算法是一种全局优化算法，其通过种群中个体共享信息的方式来求得最优解[8]。假设粒子i在解空间中进行搜索，其位置表示为xi，其速度表示为vi。粒子在搜寻最优解的过程中不断更新位置与速度，更新公式为

(1)

(2)

w=wmax-(kn/kmax)(wmax-wmin)

(3)

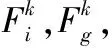
(4)

(5)

为使PSO算法搜索更加精细，本文对更新公式中权重w做出非线性改进。改进式如下

(6)

当迭代次数kn较小时，惯性权重w接近权重最大值wmax，此时粒子搜索速度快，可较快定位最优解大致范围。随kn不断增大，w在tan函数作用下，以非线性快速递减，粒子将在最优解附近精细搜索。通过对惯性权重的非线性改进，可有效约束粒子飞行速度，同时增加粒子搜索精细程度。

1.2 GRU神经网络

GRU单元结构如图1所示[9]。与LSTM模型不同的是，GRU模型中以更新门zt代替LSTM单元结构中遗忘门与输入门的作用，减少了参数量，提高了运算速度。GRU模型计算过程如下

图1 GRU单元结构

rt=σ(Wr·[ht-1,xt])

(7)

zt=σ(Wz·[ht-1,xt])

(8)

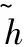
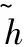
(9)

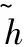
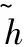
(10)

式中 ⊙为Hadmard乘积，W为权重。当前时刻状态ht，通过与门控单元权重和激活函数结合最终得到预测值，公式如下

yt=σ(Wo·ht)

(11)

式中yt为预测值，σ为Sigmiod函数。

1.3 IPSO-GRU神经网络燃气负荷预测模型

本文通过改变PSO算法的惯性权重w对其做出改进，并使用改进的PSO算法对GRU神经网络权值进行求解。将GRU模型中的权重参数看作IPSO中的粒子，并将模型相对误差ε设为适应度函数，在不断更新粒子位置的过程中，搜寻全局最优权重使适应度值达到极小。适应度函数定义如式(12)

(12)

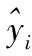
具体流程如下：1)初始化GRU网络权重w、预设GRU模型网络层节点数。初始化粒子群，粒子群参数由GRU门控单元权重组成。设定加速系数c1,c2、粒子速度范围vi∈[-Vmax,+Vmax]，给定数据样本集X={x1,…,xj,…,xn}；2)初始化样本集X中粒子群位置，根据式(4)计算此时个体级值pi，根据式(5)计算群体极值pg，根据式(2)初始化每个粒子的速度；3)根据式(1)更新粒子位置，更新此时个体适应度值和群体适应度值，记录此时个体极值pi和全局极值pg；4)根据适应度函数式(12)，计算每个粒子的适应度值，更新个体极值pi和全局极值pg，据式(2)更新粒子群速度；5)判断此时迭代次数是否达到kmax或pg小于相对误差ε。若是，则将最优粒子赋值给GRU模型门控单元权重，否则k=k+1，返回步骤(3)；6)经IPSO算法寻到最优权重的GRU模型按照式(7)～式(11)进行训练，输出燃气负荷预测值。

2 模型建立与分析

2.1 模型输入变量选取

通过研究发现[11]，在所有影响燃气负荷的因素中，气象因素对其影响程度最为明显。其次，影响燃气负荷的气象因素主要为温度与相对湿度，而其他气象特征如光照强度、风速等对燃气负荷影响较小。为减少模型输入复杂度，本文采用皮尔逊相关系数法分析了气象数据，最终得到对燃气负荷影响程度较高的气象因素。

皮尔逊相关系数计算式如下

(13)

式中E为期望，cov(X,Y)为协方差，σ为标准差。相关度可通过相关系数绝对值判断，其绝对值愈接近1，相关性越强。其中，0.8～1.0极强相关，0.6～0.8强相关，0.4～0.6中等相关，0.2～0.4弱相关，0.0～0.2不相关。由表1及图2可观察出，温度与燃气负荷呈现极强相关性，相对湿度与燃气负荷呈强相关性，而光照强度及风速与燃气负荷的相关性较低。综上选取温度与相对湿度结合历史燃气负荷共同作为模型的输入变量，模型输出为下一时刻燃气负荷。

表1 相关系数

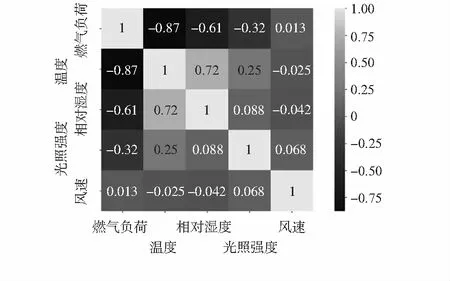
图2 相关系数热力图

2.2 数据处理

本文采集了某地区2018年11月～2019年12月的燃气负荷与温湿度数据，其部分数据如表2，其中，T(k)为温度、H(k)为相对湿度、L(k)为燃气负荷值。

表2 部分数据信息

对输入数据归一化，公式如下

θ2=(θ1-θ1min)/(θ1max-θ1min)

(14)

式中θ为T,H,L;θ1为原始数据，θ2为归一化数据；θ1min和θ1max为原始数据的最小值与最大值。

2.3 实验环境及参数选取

本文实验编程语言为Python3.7，框架采用TensorFlow1.14.0版本，硬件配置为i5处理器。加速系数可调整粒子向个体或群体最优方向飞行步幅。因此，c1和c2取值不同也关系到模型的预测效果。为选取最优加速系数，本文经多次实验得到结果如图3所示。

图3 不同加速系数适应度曲线

由图3可看出，当加速系数取c1=2.0，c2=1.4时，IPSO模型的适应度函数收敛最快且适应度值，即ε最小，此时模型效果最佳。对表3中参数进行多次调整后发现，当IPSO-GRU模型的参数设置如表3所示时，模型预测效果最佳。

表3 IPSO-GRU模型参数

2.4 模型预测效果对比分析

如图4所示，通过1 000次迭代后IPSO算法仅需较少的迭代次数即可寻找到最佳适应度值，且相较于PSO算法搜索更加精细。使用IPSO算法后预测模型的目标函数ε相较于PSO算法更小，证明了IPSO优化算法的有效性。

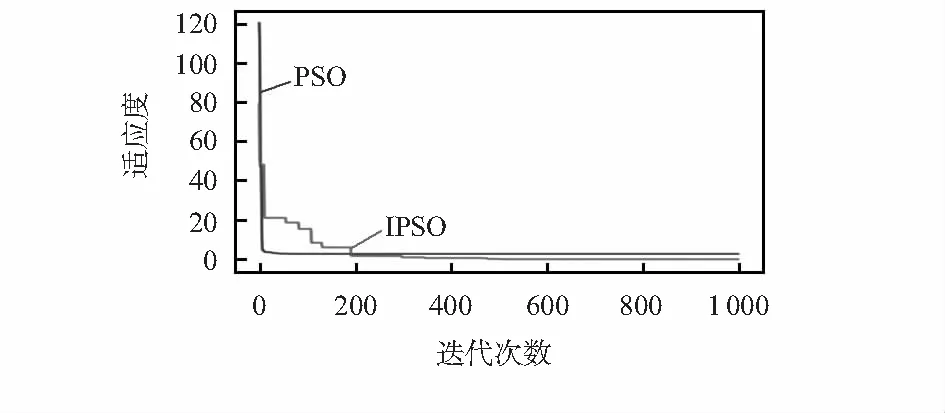
图4 不同加速系数适应度曲线

根据表3设置IPSO-GRU模型参数，设定训练目标ε=0.001。LSTM与GRU模型学习率设为0.01，其余参数与IPSO-GRU模型相同。训练结束后，使用验证集进行验证。

图5为3种模型对未来48 h燃气负荷值的预测结果曲线。由图可知，3种模型均能对燃气负荷进行有效预测，其中LSTM模型与GRU模型误差较为接近,但均大于IPSO-GRU网络模型，IPSO-GRU模型的预测值更加贴近真实值，预测效果最佳。

图5 不同模型预测结果对比

图6(a)为3种模型的绝对误差，可发现LSTM模型与GRU模型的绝对误差在40～80 m3/h，较为接近；而IPSO-GRU模型的绝对误差最小，小于30 m3/h。图6(b)为3种模型的相对误差，图中显示LSTM网络模型以及GRU网络模型平均相对误差率为2.5 %，而IPSO-GRU模型的相对误差率在1 %以下，预测误差最小。

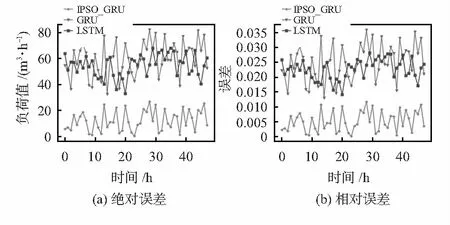
图6 不同算法误差对比

2.5 模型性能指标

选取衡量模型性能较为常用的3种指标，分别为均方根误差(root mean square error,RMSE)、平均百分比误差(MAPE)、以及决定系数(R2)[12]。

由表4可知，本文所提的IPSO-GRU模型的RMSE以及MAPE最小，分别为15.11和0.52，模型的决定系数R2最大，为0.94。

表4 模型误差指标对比

3 结束语

本文模型采用相较于LSTM模型结构更简单的GRU模型作为主体预测模型，减少了运算时间。同时，使用IPSO算法对GRU模型的改进，既增加了PSO算法搜索最优参数的精细程度，还解决了传统GRU模型寻优过程中容易陷入局部极小值问题。通过对比实验可知，IPSO算法优化GRU神经网络的燃气负荷预测模型平均相对误差在1 %以内，RMSE以及MAPE最小，模型决定系数R2最大。满足燃气实际工程需要，可为燃气的调度与分配提供有效参考依据。