基于应变模态振型的复合材料梁结构损伤位置辨识*
常海涛, 邵敏强, 曾 捷, 张胜发, 蔡福建, 孙阳阳
(1.南京航空航天大学 机械结构力学及控制国家重点实验室,江苏 南京210016;2.陆军工程大学 国防工程学院,江苏 南京 210007)
0 引 言
飞行器在服役期间,环境通常非常恶劣,在意外载荷冲击、疲劳冲击等环境因素作用下,往往会使结构产生损伤。目前,复合材料结构损伤监测已成为飞行器结构健康监测领域的热门方向[1,2],开展针对结构损伤的快速辨识监测,对于保障飞行安全,提升飞行品质具有重要意义[3]。
结构出现损伤后会使其质量或刚度等属性发生变化,导致模态参数产生变化,从而使振型发生变化[4]。振型变化是损伤位置的函数,可作为判断结构损伤状态的依据。利用振型进行损伤识别时,主要比较结构完整状态与损伤状态下的振型差异,通过振型突变来确定结构发生损伤的大致区域[5]。Cui H Y等人[6]利用薄板结构损伤前后应变振型变化,实现了单损伤与多损伤试验验证。Anastasopoulos D等人[7]将应变模态振型作为损伤特征因子,通过对梁结构进行损伤试验,验证了其可识别损伤位置。吴加权等人[8]定义了一个新的应变模态振型系数,通过简支梁试验,验证了此方法可用于工程结构损伤识别。
基于结构振动特性的损伤监测中,对局部微小损伤辨识是一个主要难题,为实现精确的损伤辨识,需要布置大量传感器测量振动应变信号。近年来,光纤光栅传感器由于具有质量轻、灵敏度高、芯径细、柔韧性好、便于分布式布局等独特优点,逐渐在结构损伤辨识领域受到广泛关注[9]。
基于上述分析,本文提出一种将光纤Bragg光栅(fiber Bragg grating,FBG)传感器与应变模态振型相结合的悬臂式复合材料梁结构损伤位置辨识方法。利用有限元Ansys Workbench软件,建立悬臂式复合材料梁结构模型。通过数值仿真,研究应变模态振型对于通孔类损伤的响应特征。在此基础上,构建了基于FBG传感器的结构损伤位置辨识系统,并加以试验验证。
1 基于应变模态振型的损伤识别原理
悬臂式复合材料结构应变模态为[10]
(1)
式中φr(x)为第r阶应变模态振型,φr(x)为第r阶模态振型,Dr=(-ω2mr+jωcr+kr)-1F(x)为分布载荷。
根据悬臂式复合材料结构应变模态推导应变模态振型损伤辨识指标
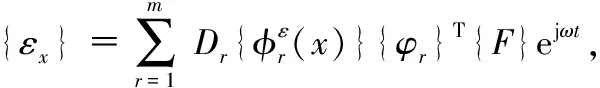

(2)

设φr为完整状态下第r阶应变模态值,{φr}d为损伤状态下第r阶应变模态值,则悬臂式复合材料结构应变模态变化差值{Δφr}可由损伤状态下的应变模态值与完整状态下应变模态值的差值得出,具体可表示为[12]
{Δφr} ={φr}d-{φr}
(3)
定义应变模态变化率{Δψr}为应变模态变化差值{Δφr} 与完整状态下应变模态值{φr} 的比值,具体可表示为[13]
(4)
由以上分析可知,应变模态变化差值指标{Δφr}和应变模态变化率指标{Δψr}均为悬臂式复合材料结构损伤位置相关的函数。
因此,本文提出采用应变模态变化差值指标与应变模态变化率指标,开展针对悬臂式复合材料结构的损伤位置辨识。
2 基于应变模态振型的悬臂式复合材料梁结构损伤位置辨识方法仿真验证
2.1 悬臂式复合材料梁结构建模
碳纤维悬臂式复合材料梁结构基本尺寸为:长度400 mm,宽度40 mm,厚度2 mm,每层纤维布厚度为0.2 mm,共10层,铺层角为0°,90°,如图1所示。为便于应变模态振型的提取,在复合材料梁结构的表面中轴线处提取21个节点,作为应变模态数据采集点。

图1 碳纤维悬臂式复合材料梁模型
2.2 基于应变模态振型的损伤位置辨识方法仿真验证
通过有限元软件模态分析,计算出21个节点处的应变模态值。分别采用应变模态振型变化差值、应变模态振型变化率2种指标,开展针对悬臂式复合材料梁结构的损伤位置辨识方法仿真验证。悬臂式复合材料梁结构损伤形式,如表1所示。

表1 悬臂式复合材料梁结构损伤形式
完整结构与单通孔损伤结构对应的前三阶应变模态振型曲线,如图2所示。

图2 完整结构与单通孔损伤对应的前三阶应变模态振型
根据图2分别计算得到悬臂式复合材料梁结构前三阶应变模态变化差值指标{Δφr}、应变模态变化率指标{Δψr},绘制成如图3所示曲线。

图3 单通孔损伤应变模态振型变化差值和变化率
由图3(a)可知,前三阶应变模态变化差值在6#节点处均发生了突变,可以有效地识别出损伤发生在6#节点,其中第一、第二阶应变模态变化差值相较于第三阶应变模态变化差值变化较小。由图3(b)可知,前三阶应变模态变化率在6#节点处均发生了明显的突变,可判定损伤发生在6#节点。由此可知,应变模态变化率指标对于悬臂式复合材料结构单孔类损伤位置具有良好的识别效果。
3 基于应变模态振型的结构损伤识别试验验证
3.1 FBG应变传感器原理
FBG传感器是一种基于光纤纤芯折射率变化的传感器,当光波光束传播到栅区时,光栅折射率会发生变化,从而导致特定波长的光波被反射,其他波长的光波则继续传输,被反射回来的反射光谱波峰对应的波长称为中心波长[14]。
FBG传感器波长计算公式为[15]
λ=2neffΛ
(5)
式中λ为栅区中心波长,Λ为折射率周期,neff为光栅有效折射率。根据式(5)知,当栅区的折射周期发生变化时,其反射波长就会发生变化。
栅区波长的偏移量与其轴向应变对应,FBG传感器轴向应变引起的波长变化量为[16]
Δλ=(1-Pe)·εx·λ
(6)
式中Pe为有效弹光系数,由Λ,neff等决定,其值为0.22。
FBG传感器中心波长偏移量与栅区应变之间是线性关联的,从而可以用栅区波长变化来表达悬臂式复合材料结构表面应变,则有
(7)
3.2 基于应变模态振型的结构损伤识别系统构建
结构动力系统中的质量分布决定着结构的动力特性,当其发生改变时,结构动力特性会变化,从而使结构动力响应产生变化。为此,试验中通过在悬臂式复合材料结构表面粘接质量块来模拟损伤。
将质量为30 g的质量块粘贴于3#传感器位置,用于模拟单损伤模式。悬臂式复合材料结构试验件,如图4所示。FBG传感器采用波分复用的方式,共2个通道。每个通道串接4只FBG应变传感器,传感器编号为1#~8#。

图4 悬臂式复合材料结构试验件
基于应变模态振型监测的悬臂式复合材料结构损伤识别系统,如图5所示。通过力锤锤击,输入脉冲激励信号,对结构进行激励。采用MOI光纤光栅解调仪实现波长信号解调,利用配套软件采集波长—应变响应信号。

图5 基于应变模态振型监测的悬臂式复合材料梁结构损伤识别系统
3.3 损伤识别试验与结果分析
试验过程为:力锤锤击完整结构和损伤结构,分别得其前三阶固有频率下对应的振幅值。通过归一化处理,拟合出完整结构和损伤结构的前三阶应变模态振型曲线。根据模态振型曲线的突变区域,确定结构损伤发生的位置。
振幅提取过程为:施加力锤脉冲激励,通过傅里叶变换方法,将FBG传感器所测信号代入应变—波长公式(7),转换为应变频域响应信号。以第一阶固有频率为例,对于完整结构,FBG3对应的应变响应幅值为19.33×10-6;对于损伤结构,FBG3对应的应变响应幅值为15.26×10-6,如图6所示。

图6 完整、损伤结构FBG 3 波长响应信号
分别求出完整结构和损伤结构中其他7个FBG 采样点处的应变幅值,计算出完整结构和损伤结构在第一阶固有频率下的应变模态振型,如图7(a)所示。由图7(a)可知,FBG 3测点附近,损伤结构相较于完整结构的应变模态振型发生突变,故可判断悬臂式复合材料梁结构在FBG3测点位置附近发生损伤。
分别计算出完整结构和损伤结构对应的第二、第三阶应变模态振型曲线,如图7(b),(c)所示。
由图7(b)可知,在第二阶固有频率下,FBG3附近区域对应的应变模态振幅值出现了突变,由此判断损伤区域发生在FBG3测点附近区域。由图7(c)可知,在第三阶固有频率下,虽然在FBG3和FBG4测点附近均出现了应变幅值变化较大的情况,但仍可判断出损伤区域为FBG3和FBG4测点区间。分析其原因可能是此阶固有频率状态下,结构的应变响应较小,导致损伤定位精度有所降低,但仍可对损伤区域做出初步判断。

图7 第一~第三阶段应变模态振型曲线
4 结 论
本文研究了基于FBG传感器和应变模态振型的悬臂式复合材料结构损伤位置辨识方法。具体内容包括:
1)借助有限元方法,构建了悬臂式复合材料梁结构力学模型。通过数值仿真方法,分别提出了基于应变模态振型变化差值和应变模态振型变化率的通孔损伤位置辨识方法。根据数值仿真结果,验证了基于上述两种指标进行损伤定位的可行性;
2)搭建了基于应变模态振型监测的悬臂式复合材料梁结构损伤识别系统,利用FBG传感器网络所采集应变响应信号,计算得到悬臂式复合材料结构损伤前后的应变模态振型。根据应变模态振型的幅值突变特征,实现对于损伤位置的辨识。

