基于交变信号源的磁定位技术研究
郝伯强,郭 锋,赖禹同,唐自强
(西南科技大学 信息工程学院,四川 绵阳 621010)
0 引 言
自从1975年梯度张量法首次被用于磁偶极子的跟踪定位以后,引起了众多学者的重视[1]。之后,多种磁梯度张量测量仪和梯度张量的定位算法都被陆陆续续地提了出来。目前,梯度张量定位技术由于其独特的性质被广泛用于地质勘探、军事和医学等领域[2]。
在磁偶极子定位系统中,传统的静态磁信号源稳定性较低,其产生的恒定磁场容易受到背景磁场、干扰噪声以及地磁场的影响,在很大程度上降低了定位的精准度[3]。因此,本文以已知频率的交变磁场作为磁信号源,有效地消除了环境磁场的影响,大大地提高了定位系统的稳定性。
本文基于梯度张量算法,研究了交变磁信号源定位系统的抗干扰效果。在已知动态磁场的变化频率的前提下,利用锁相放大器提取出直流信号,通过定位算法即可得到磁信号源的位置信息。通过MATLAB软件对定位系统建立仿真模型,比较了在不同大小的噪声干扰下静态磁源定位系统和动态磁源定位系统的稳定性,并分析对比了二者在不同条件下的定位效果。
1 磁梯度张量算法原理
1.1 磁梯度张量性质
磁场梯度张量是指磁场的3个分量分别在3个方向上的变化率。由于现有磁传感器一般是测量磁感应强度,因此,要进行磁梯度张量的测量就需要构造测量阵列来测量磁场在3个方向的变化率[4]。
设Bx,By,Bz分别为磁场分别在x,y,z三个方向上的分量,则磁梯度张量表示为[5]

(1)
由于磁场是无散场,其任意点处的散度为0,且在没有空间电流密度的情况下为无旋场,因此,可以得到
(2)
(3)
由式(2)和式(3),可以得到
Bxy=Byx,Bxz=Bzx,Byz=Bzy,Bxx+Byy+Bzz=0
(4)
由此可以看出,张量表达式中的元素本来有9个,通过磁场的无旋性与无散性的性质推导化简,其中的4个元素可以被其他的5个元素表示,因而只有5个元素是相互独立的,只要知道了其中的5个元素即可获得完整的张量矩阵。
1.2 磁梯度张量定位方法
在实际分析和研究中,当目标与测量系统之间的距离大于2.5倍目标尺寸时,则可以将目标视为磁偶极子[6,7]。磁偶极子产生的磁场称为磁偶极子场,如图1所示。磁偶极子场中任意一点的磁感应强度的表达式为[8]
图1 磁偶极子场
(5)
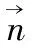
(6)
同时,将两点的磁感应强度写成三份量的形式,那么,两点磁感应强度的差值又可以表示为
(7)
显然,式(7)中的矩阵就是磁场的二阶张量,即磁梯度张量,由式(6)和式(7)可以得到

(8)
式(8)为单点反演定位算法的定位公式[9]。
2 磁梯度张量测量阵列
常见的梯度张量测量阵列的结构有三角形、十字形、正四面体和正六面体等。根据梯度张量中的9个元素只有5个元素互相独立这一原理,可以将测量阵列简化为十字形,并且经过仿真验证,图2所示的测量阵列结构是只利用4个及以下数量的三轴传感器构成的所有阵列结构中最优[10,11],因此,本文选择该阵列作为测量阵列进行研究。

图2 十字形测量阵列
在图2中,S1,S2,S3,S4为三轴传感器,测量阵列中心的磁感应强度可以用4只传感器的的平均值来近似得到
Bo=(B1+B2+B3+B4)/4
(9)
对角线上的2只传感器之间的距离称为基线距离,设基线距离为d,由式(1)可得测量阵列中心处的梯度张量为
(10)
3 磁场信号解调原理
磁信号源产生的磁场信号会被传感器阵列接收,之后通过提取该正弦信号的幅值,以梯度张量算法实现定位。然而传感器接收到的正弦信号属于微弱信号,幅度太小,信噪比太低,再加上传感器自身带来的系统误差,最终的定位效果会受到较大的影响,因此,需要借助锁相放大器来完成正弦磁场信号的提取和解调[12]。锁相放大器的工作原理如图3所示,输入信号与已知频率相位的参考信号通过乘法器,经过积分计算后的输出再通过低通滤波器,即可得到一个与频率无关的直流信号,完成信号的解调。

图3 锁相放大器组成结构
设含有噪声的输入信号和通到参考通道的参考信号的表达式分别为
Si(t)=Asin(ωit+θ)+N(t)
(11)
Sr(t)=Bsin(ωrt+φ)
(12)
式中A,B分别为输入信号和参考信号的幅值;ωi,ωr分别为输入信号和参考信号的频率;θ,φ分别为待测信号和参考信号的初始相位;N(t)为噪声信号。
输入信号和参考信号经过相敏检波器相乘、积分后的输出为[13]
-cos[(ωi+ωr)t+(θ+φ)]}dt
(13)
从式(13)中可以看出,经过相敏检波器后的输出信号中包含了2个不同频率的非直流信号。令ωi=ωr,θ=φ,则经过低通滤波器后,非直流信号会被滤掉,即可得到一个直流信号
So=AB/2
(14)
4 仿真结果与分析
根据磁梯度张量定位原理和前文提到的测量阵列,分别对恒定磁场目标和交变磁场目标进行定位仿真实验,并对结果进行比较。
仿真过程中,分别在传感器测量阵列叠加不同大小高斯白噪声,来模拟静态磁源和交变磁源周围的环境噪声。不加噪声和加入信噪比分别为230,210,200 dB的高斯白噪声时的仿真结果如图4所示。
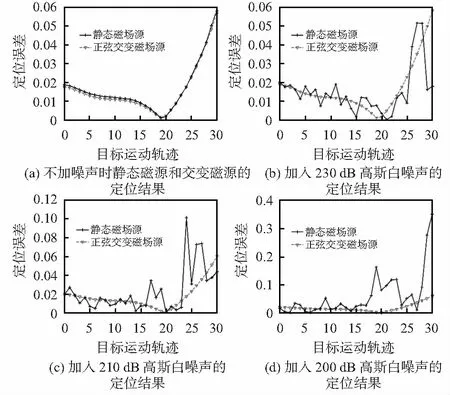
图4 叠加不同大小噪声的定位误差
从图4中的仿真结果可以看出,当环境中的噪声增大时,静态磁场源的定位误差也会逐渐增大,而对交变磁性目标进行定位的误差则基本不受影响。当不加噪声,只考虑地磁场和传感器测量误差的影响时,对静态磁源和交变磁源定位的绝对误差基本保持在0.02 m以下,最大误差分别为0.058 m和0.056 m,此时的相对误差分别为0.89 %和0.86 %;当加入200 dB高斯噪声时,随着定位距离的增大,静态磁源的定位误差明显增大,最大绝对误差为0.35,此时两种磁目标的相对定位误差分别为5.4 %和0.95 %,可见基于交变磁场源的定位具有非常优秀的抗干扰能力。
5 结 论
本文研究了同等条件下静态磁场源和交变磁场源定位系统的定位精准度和抗干扰能力。利用锁相放大器对传感器接收到的正弦信号进行解调,得到与原始信号幅值相等的直流信号,即可通过单点定位算法实现对磁性目标的定位。锁相放大器在对正弦信号解调的同时,也过滤掉了环境中的噪声,因此,该交变磁源定位系统能在很大程度上抑制噪声对定位结果的干扰。通过对静态磁源和交变磁源定位系统的仿真结果进行比较,结果表明,后者受环境噪声的影响较小,定位结果明显优于前者。由于本文中的解调步骤需要已知交变信号源磁矩的频率和相位,因此在下一步的工作中,需要设计出可直接得到信号频率和相位且能自由调节大小的信号发射源。

