高过载小量程加速度计结构优化与特性分析*
刘思远,苏淑靖,许福佳
(中北大学 仪器与电子学院 省部共建动态测试技术国家重点实验室,山西 太原 030051)
0 引 言
随着微细加工技术的发展,硅基微机电系统(MEMS)加速度计作为商业化的 MEMS 器件受到了许多关注。MEMS 压阻式加速度计利用半导体硅的压阻效应,在机械能与电能之间搭建了一种简单的能量/信号转换平台[1],由于其结构与制造工艺简单、具有低输入阻抗以及后续信号处理电路简单,所以,在民业、工业和一些恶劣环境中得到了广泛的应用[2]。
1979年,Roylance L M与Angell J B首先成功研制出单悬臂梁加质量块结构的加速度计[3]。此后,世界上许多国家开始对提高压阻式加速度计的性能展开研究,设计了不同结构的 MEMS 加速度敏感芯片。例如Lim M K等人提出了一种微梁直拉直压的加速度计模型[4];董培涛等人研制了一种带有梳齿阻尼器的“三梁—质量块”压阻式加速度计[5];Li Y F等人研制了一种非对称间隙悬臂梁结构的加速度计[6];王鹏等人设计了一种具有复合八梁结构的加速度计[7]。但由于设计或工艺方案难度原因,上述加速度计灵敏度与固有频率相互制约的矛盾仍较为突出。
面对灵敏度与固有频率相互制约这一在压阻式加速度计现阶段设计中普遍存在的难题,本文对传统四边固支梁结构做了进一步优化,提出了一种全新的带有支撑梁和微梁的压阻式加速度计结构,在保证灵敏度的前提下实现高固有频率以及较好的抗过载能力。
1 压阻式加速度计结构优化设计
高灵敏度与高固有频率的相互协调作为设计高过载小量程加速度计的重点,必须在保证结构稳定性的同时,又要满足带宽与合适的阻尼比[8],依据实际需要,设定以下指标要求:1)满量程A=100gn;2)固有频率f≥30 kHz;3)灵敏度理论值S≥50 μV/gn;4)抗过载能力为10 000gn。
优化设计的带有微梁与支撑梁的加速度计芯片结构如图1所示。该结构中,处于中心的质量块通过8根支撑梁和4根微梁与硅基框架相连。支撑梁主要实现对质量块的支撑,提高整体结构的固有频率,在2根支撑梁中间的微梁由于宽度及厚度均远小于支撑梁本身,利用其产生的较大微应变,实现信号的有效测量。
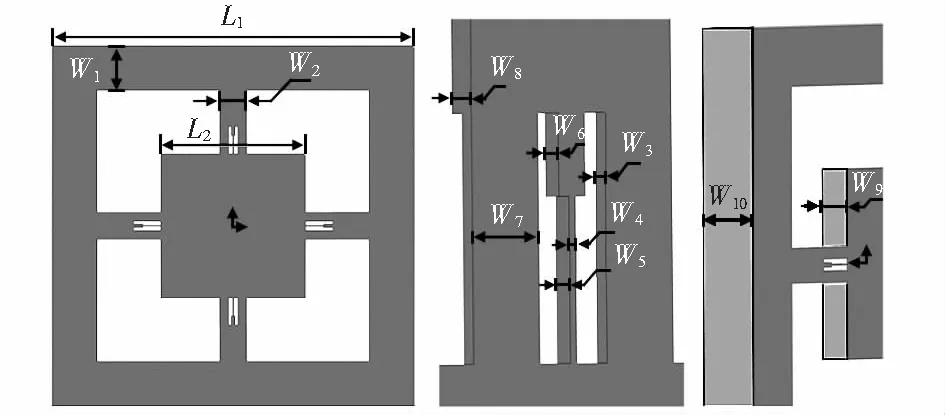
图1 加速度计结构示意
结合固有频率、灵敏度等因素的影响,同时在考虑加速度计性能和制造方法后,对加速度计结构参数进行优化,优化后的尺寸参数如表1所示。

表1 加速度计参数值 μm
2 加速度计仿真分析
2.1 微梁应力、应变、挠度分布分析
由于在本文结构中,微梁根部为受力最集中区域,同时也是压敏电阻布置区域,故对其进行分析。所选取的分析路径AB为从x轴上一侧支撑梁与微梁连接处经过质量块中心到另一侧相同连接处,如图2所示。
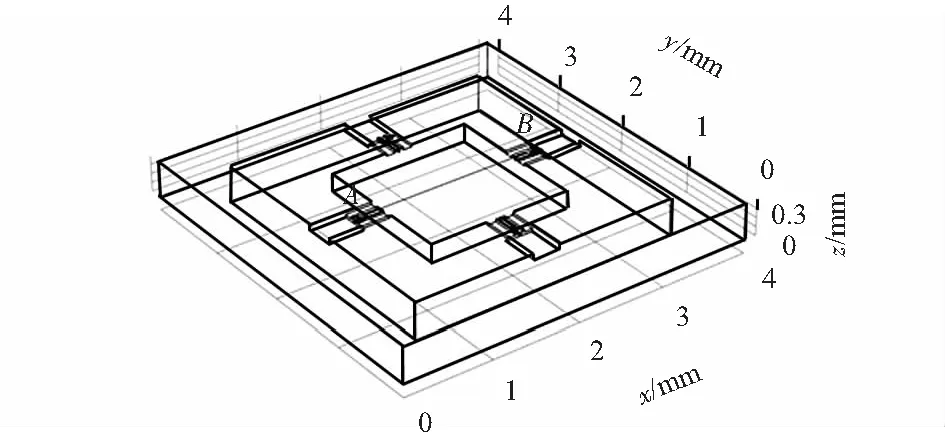
图2 结构上选取路径示意
2.1.1 应力与应变分析
表面牵引力,也即作用在内部基准面上的应力,通常可以分解为3个相互正交的分量[9]。其中,垂直于表面的分量称为正应力,与表面相切的2个分量称为剪应力。图3(a)为z轴加速100gn时应力仿真结果。其中,应力σxx,σyy和σzz为正应力。由于处于静力平衡状态,剪切应力关于对角线对称(即σxy=σyx,σyz=σzy,σzx=σxz)。纵向应力(σxx)高于横向应力(σyy和σzz)。σxx在微梁与质量块接触端附近最大,值为2.6 MPa。
与应力相似,应变同样具有9个分量,而这9个分量也同样可以用6个分量表示。图3(b)为z轴加速度100gn时应变仿真结果。图中,应变张量εxx,εyy,εzz为正应变。在静力平衡的作用下,剪切应变关于对角线对称(即εxy=εyx,εyz=εzy和εxz=εzx)。
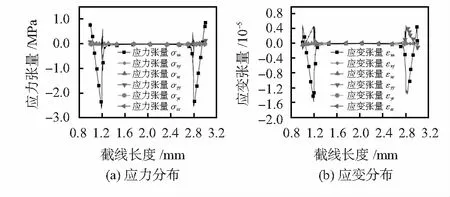
图3 沿路径上应力、应变曲线
2.1.2 挠度分析
在加速度计挠度分析之前,做出如下2点假设,有助于计算更加简单:1)设计时考虑的是单层硅梁,而实际上硅梁为多层结构;2)梁可以简化为2段变截面悬臂梁,而质量块可以等效为一矩形,易于计算。
梁—质量结构由框架支撑,然后与底面底座连接。梁的具体参数如图4所示,靠近质量块端的支撑梁高度为(ξ+η)h/2,长为l1;靠近框架一端的支撑梁高为(1+ξ)h/2,长为l2,截面惯性矩记作IB,两梁宽均为b,梁总长为l1+l2=l。当结构沿z轴受到冲击时,固支梁在端点受到集中载荷P。
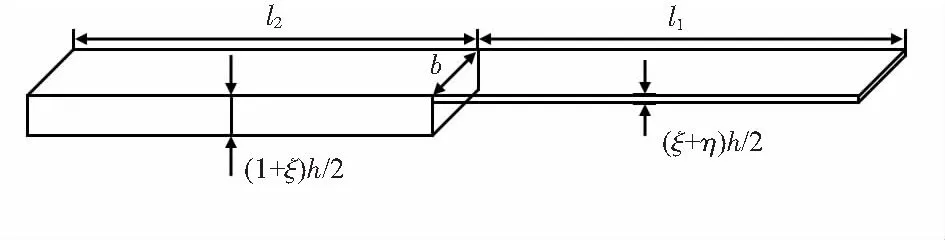
图4 支撑梁与微梁简化示意
取l1段平均截面惯性矩记作IA
(1)
取l2段平均截面惯性矩记作IB
(2)
取梁与质量块接触端的挠度记作w,则w=w1+w2+w3+w4。其中
(3)
则
(4)
取l1=al,l2=bl,IA=cl,IB=d′l,则梁端部挠度为
(5)
(6)
当加速度计受到来自工作方向的加速度时,由于惯性力的作用,质量块的位移方向与加速度的方向相同。如图5所示,梁变形呈S形,梁端部最大挠度为26.1 nm。
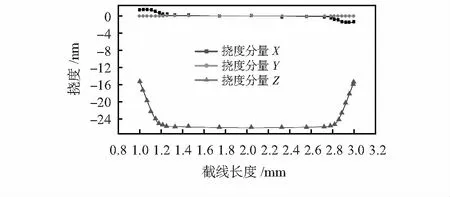
图5 沿路径上挠度曲线
2.2 加速度计模态分析
结构的模态影响结构的灵敏度和带宽,利用Comsol 软件对结构的模态分布进行了分析。图6给出了前4个振型的仿真结果,其固有频率如表2所示。
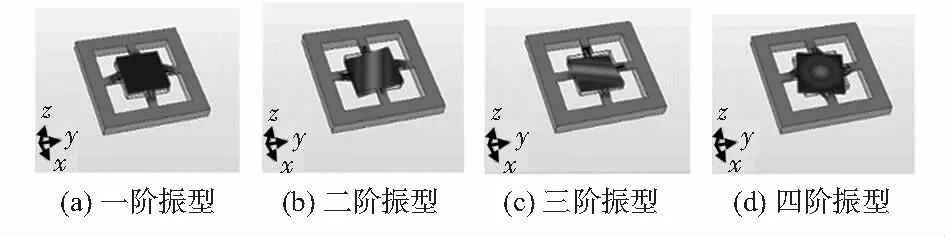
图6 前四阶模态振型

表2 模态分析结果
图6将框架的底面固定,观察结构变形情况。由图6(a)可以看出,一阶模态为工作模态(质量块沿z轴运动,框架静止,质量顶面与x-y面平行),其固有频率为31.122 kHz,为传感器提供了较宽的测试带宽。在二阶模态和三阶模态下,质量分别沿x轴和y轴旋转,固有频率分别为45.202 kHz和45.206 kHz。这两种模态的固有频率应该是相等的,在Comsol 中,网格划分造成了这种差异。图6(d)为结构的四阶模态,固有频率为178.79 kHz,框架和质量块绕z轴运动。由表2可以看出,其他模态远大于一阶模态,有助于减少模态干扰,加速度计可以稳定工作。
2.3 加速度计灵敏度分析
高过载小量程加速度计采用惠斯通电桥结构,4个压敏电阻被设计对称分布在4根微梁上。由于加速度计受到z轴负向的惯性力,质量块带动微梁发生形变,从而引起压敏电阻阻值发生变化,电桥失衡进而导致输出电压变化,具体表现为
(7)
对于压阻式加速度计,其灵敏度取决于压敏电阻上的应力分布,灵敏度的表达式如下
(8)
式中Uout为输出电压,Uapplied为加速度计给定惠斯通电桥输入电压,R为压敏电阻的阻值,π为P型硅的压阻系数,根据材料参数取7.18×10-10Pa-1,σ为压敏电阻在给定加速度下受到的应力。由实际条件可取Uapplied为3.3 V,aapplied为100gn,σ为2.6 MPa,故由式(8)可求得在该加速度下,输出灵敏度为60.9 μV/gn。
2.4 加速度计抗过载能力分析
加速度计芯片过载损坏的主要原因是由于过高的加速度使得质量块产生较大的位移,梁上根部的应力瞬间增加至抗张强度,最终超出材料许用应力。在静态条件下,对加速度计施加过载10 000gn加速度情况下应力与位移分布情况如图7(a),(b)所示,可以得到此时结构最大位移量为2.606 3 μm,梁上所受最大应力为300.04 MPa。限位间距为1 μm时,当质量块与盖板发生接触,如图7(c),(d)所示,此时加速度计所受载荷达到3 836.8gn,梁上最大应力为115.12 MPa,之后随着载荷的增加最大位移保持恒定。
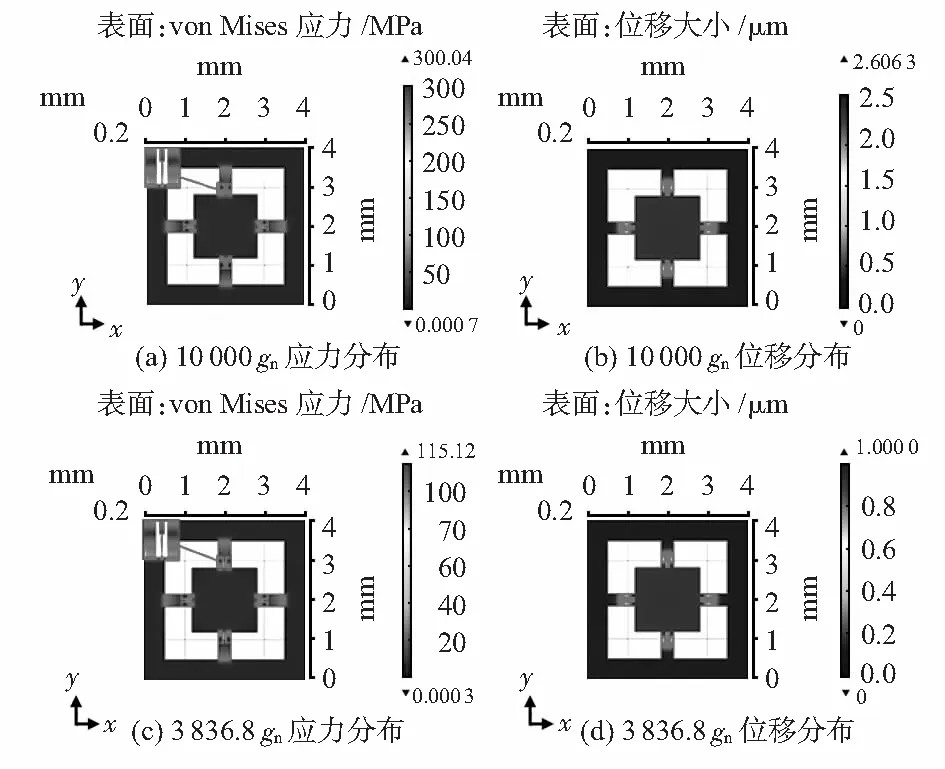
图7 10 000 gn与3 836.8 gn过载下应力、位移分布
综上可知,梁结构在10 000gn加速度下所受最大应力300 MPa远小于硅的许用应力340 MPa,故此加速度计抗过载能力可以达到10 000gn。需要注意的是,量程范围内,质量块不能触碰到上、下盖板,否则会产生较大的非线性误差。据此可确定最大限度提高抗冲击能力的限位间距,即d等于器件满量程时质量块的位移(26.1 nm),采用此值作为限位间距。
3 结 论
本文针对传统高过载小量程加速度计进行了优化设计,通过引入微梁,在不牺牲固有频率的前提下,使得加速度计本身的灵敏度得到有效提升。利用Comsol软件对该敏感结构进行有限元仿真,通过获得的应力、应变分布,固有频率、灵敏度等指标,验证了加速度计结构的合理性,满足设计指标要求。

