图式分析法:隐性显化的可视化过程
刘建国, 吴玉珠, 殷亚萍
(栖霞中学,江苏 南京 210046)
图,指数学中的图形(涉及函数图象、几何图形、统计图形);式,数学符号语言,问题的代数表达(如代数式、方程、不等式等).图式分析法主要是借助问题的条件与结论之间的差异,通过图形的形式直观地呈现问题的条件与目标,并在图形上分析问题,显现问题的条件与目标,从而在图像上显现问题的本质与内在联系,配合以代数语言表达,呈现解题的思维过程,最终实现解题的目标[1].在图式分析过程中体现隐性显化的思维可视化,其方法是化抽象文字语言为形象的图形语言,化形象的图形语言为具体的代数语言.
1 数学问题的剖析
数学问题是由条件与结论构成的,条件和结论之间存在着3个维度的关系:首先条件与结论表象上具有差异性,其次条件与结论之间存在着内在联系性,最后条件与结论具有可转化性.三者相互渗透,相互制约,正是由于条件与结论的这3个维度的关系,使得问题表面上是条件与结论之间的逻辑关系,实际上是数学思维体现的形式,从差异性到联系性再到转化过程,实际上是数学问题的表象到问题本质再到问题表达的一种思维路径.

图1 图式分析法基本框架
图式分析法主要是通过“差异直观化,联系可视化,转化自然化”,最终在图形中“发现差异,寻找联系,实现转化”(如图1),在实际解题过程中跨越思维障碍、化抽象为具体的问题分析方法.
2 图式分析法的基本功能
2.1 图式直观化(发现差异)
由于条件与结论的差异性,使得问题难易程度不同.一般情况下,当条件与结论差异越大时,解题者难以寻找内在联系,建立相应的数学模型,此时问题不易解决;当条件与结论差异越小时,解题者较容易寻找其内在联系,此时问题解决较易.一般情况下,问题所呈现的条件与结论均为代数语言或者文字语言形式表达,晦涩难懂,且不易理顺,若将条件与结论(目标)以图形的形式表达,使得条件显现化,目标可视化,从而清晰地表达问题的核心,有助于分析问题与解决问题.
2.2 图式可视化(寻找联系)
数学试题本质上是命题者在条件与结论之间设置一些思维障碍,解题者需将这些障碍呈现在解题过程中.将条件与目标呈现在图像后,可根据所构造的图形建立相应的模型,不同的构图形式会呈现不同的数学思维.通常情况下,图式分析法寻找条件与结论的联系的思维主要有3种形式:1)直接性思维,从图形上呈现的条件出发,按照一定的逻辑顺序推理至结论;2)逆反性思维,主要采用分析法,从图像中表达结论(目标),在结论中寻找与条件之间的联系;3)逆反与直接性思维相结合,从条件与结论同时出发,化归至统一的思维方式.在差异直观化的前提下,所需寻找的联系就会在图像上显现化,当然对于同一个问题,不同的图形表达将会导致差异性不一致,在寻找联系时也会得到不同的联系方式,因此这种可视化只是针对特定的图形.
例1已知⊙M:x2+y2-2x-2y-2=0,直线l:2x+y+2=0,P为l上的动点,过点P作⊙M的切线PA,PB,切点为A,B,当|PM|·|AB|最小时,直线AB的方程为
( )
A.2x-y-1=0 B.2x+y-1=0
C.2x-y+1=0 D.2x+y+1=0
(2020年全国数学高考Ⅰ卷理科试题第11题)
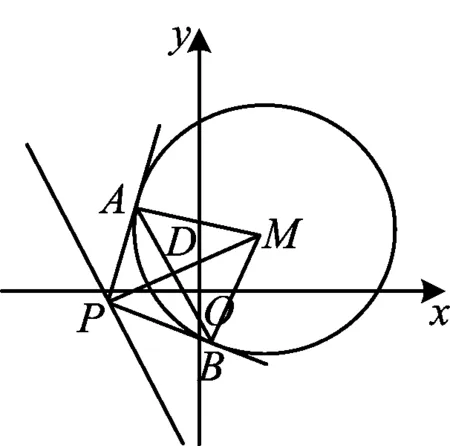
图2
图式分析根据题设中的条件作出图形,联结AM,BM(如图2),由题意可知M(1,1),四边形PAMB的面积为
当|PM|·|AB|最小时,S最小.因为
S=2S△PAM,
所以只需|PA|最小.在△PAM中,
即只需|PM|最小.当|PM|最小时,PM⊥l,直线PM的方程为
即
与直线l联立解得x=-1,y=0,故P(-1,0).
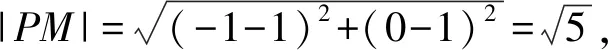
又点A,B在以P为圆心、1为半径的圆上,即⊙P的方程为
(x+1)2+y2=1,
⊙P与⊙M的方程相减可得
2x+y+1=0,
即直线AB的方程为
2x+y+1=0.
故选D.
逆反性思维设直线AB:y=kx+b,可知
从而
又
PM⊥AB,PM⊥l,
于是
l∥AB,
即
k=-2,
故直线AB的方程为y=-2x+b.
由垂径定理可知
DM⊥DB,
得
|DM|2+|DB|2=|MB|2,
即
又
从而
即
解得b=-1或b=7(舍去),于是直线AB的方程为
2x+y+1=0.
故选D.
2.3 图式自然化(实现转化)
将题设的条件与结论以图形的形式直观呈现,即文字语言向图形语言的转化过程(代数图形之间的转化),用以将抽象的问题具体化,从而更方便地寻找条件与结论之间的联系.在凸显联系之后,解题者需要将图形的数量关系、位置关系以及变换关系以代数的形式表达,即图形代数之间的转化,本质上是一种对问题的表述与翻译(如图3).这种转化过程体现了图式分析法在解题过程中转化自然化,使得解题思路清晰、表达顺畅.
例2若过点(a,b)可以作曲线y=ex的两条切线,则
( )
A.eb C.0 (2021年全国数学新高考Ⅰ卷试题第7题) 直观化如图4,根据题意画出函数y=ex的图象,由于点(a,b)的位置不确定,故切线不确定,选项无法直接表达在图象上,差异性较大. 图4 图5 图6 可视化通过作图,画出过点(a,b)的两条切线,进一步确定点(a,b)的大致区域(如图5). 自然化根据点(a,b)的位置,作直线x=a与y=ex的交点为(a,ea)(如图6),可得ea>b,即0 图式分析法是集文字语言、代数语言与图形语言于一身,在实际解题过程中,3种语言之间的转化是等价的.这种等价性体现在将题干中的文字语言转化为图形语言,以及在寻找联系后将图形语言转化为代数语言的过程.但在3种语言转化过程中应注意转化的准确性与简洁性,避免造成不必要的错误与运算的烦琐.此外,等价性也体现在抽象问题直观化,从而达到思维可视化. 图式分析法视角下,对题设的条件与结论构造的图形不一致将导致寻找联系的思路不一致,从而在代数语言表达时就会产生不同的形式.同样地,在同一个图形中,图形的位置关系、数量关系的表达形式不一致,也将导致呈现的解题过程不同,因而就会产生一题多解;当然,不同的题目在图式分析时,会有同一个类似的图形呈现,也就会出现类题一解的现象.一题多解与类题一解实质上是数学模型建立的过程,图式模型化是将各个数学知识模块进行整合与应用,也可用于解决实际问题.图式模型化是问题直观性的体现,也是数学知识图式呈现的体现,更有助于对数学知识的理解与应用. 图式分析法在解题过程中往往会出现一题多图、一图多种表达形式,此时应该对图形与代数表达进行甄选,这种甄选具有普遍意义.如何甄别图形的优劣、代数表达的简洁,从而选择恰当的图形,准确地表达解题过程是图式甄别的基本原则.在甄选时,可以在原有图形上进行改造,通过几何的知识对图形进行改造(如作辅助线、图形变换等),显化目标,进而进行甄别,在代数运算上进行优化,从而达到表达精准、运算简洁的目的. 如例2中,将题设条件等价地表达在图形上,在图象上找出条件与结论之间的内在联系,可快速寻找到点(a,b)的位置,使得问题表达简洁.当然解决例1采用的主要是一图多种形式表达,因此呈现出直接性思维与逆反性思维,当然在图2中寻找联系还可以通过求出切线PA,PB的方程,找出切点A,B的坐标,利用两点式求出直线AB的方程.下面笔者给出一道一题多图的类型. (2020年全国数学高考Ⅱ卷理科试题第15题) 则 即 图7 图8 图9 即 则点O到直线AB的距离为 可知点B在y轴上.由|z2|=2,知B(0,2).又 即 于是 得 波利亚在《怎样解题》中提出:“解题必须弄清问题,回答一个尚未弄清的问题是愚蠢的.”[2]审题是为了理清条件和结论之间的内在联系,本质上是弄清问题.图式分析法可以深刻地反映问题的本质与内部联系,具有普适性.图式分析法在审题时应兼顾条件与结论,而非只是对条件进行审查.在审题时,以图形为载体,呈现问题的条件与结论(目标),分析条件与结论的图形意义,只有在审题过程中兼顾条件与结论,才能更快地寻找到条件与结论之间的联系,为解题创造一个必备的条件. 图式分析是图式审题后一个重要的步骤.在审题过程中,凸显条件与结论在图形中的表达,借助代数形式表达图形中的若干关系,即式中有图,图中有式.分析是将审题与图式表达过程中的思路进行梳理,如何精准地表达问题与解题思路是解决问题的关键.由于解题者在审题过程中所构造的图形不同,呈现的数学思维就不一致,这就导致解题方法不一致,从而需要对每种思维进行筛选,于是就需进入下个环节——图式探路. 图式探路是建立在图式审题与图式分析之后的重要过程,它是宏观上条件与结论的联系方式实现转化的一种微观呈现.在图式分析过程中,由于图形构造的不同会产生不同的路径,此时解题方法不止一种,而每种方法各有优劣,因此怎样选择是关键.当选择一种路径时,在运算过程中发现运算量大且不易将图形中的相关关系表达准确时,应该重新选择一种新的路径进行尝试或者重新对问题进行图式审题与图式分析,不是每一种图式所表达的条件与结论之间的联系都能解决问题,因此在图式分析过程中,应注重图式的分析与表达是否合理.通常情况下,图式探路与审题和分析是分不开的,在审题过程中探索解题路径,在路径探索中对问题进行审查. 图式检验是图式分析法解决问题的最后一步,由于在审题、分析以及探路环节中都有可能出现不同程度的差错,导致问题解决功亏一篑,因此在解题后对问题进行校对十分必要.题后检验不只是对结果进行检验,而是贯穿于整个图式分析过程中,应注重逆向思维的应用,图式检验可以直接进行检验,也可将所得结论置于图形中,通过图式分析法进行逆向的反推,直至与条件吻合时,才能确定最终结论是否正确. ( ) (2019年全国数学高考Ⅱ卷理科试题第11题) 图式审题将题设中的条件呈现在图形中,在读题时构造相应的图形(如图10所示). 图10 图11 图式分析结论是求离心率,即双曲线基本量的等式关系,条件|PQ|=|OF|是确立等式关系的关键,因为|OF|=c,所以如何表达是关键.从图形中不难发现PQ是圆x2+y2=a2的一条弦,即由垂径定理可以求出|PQ|.如图11,首先要求出|OD|,即点O到直线PQ的距离,直线PQ的方程是关键,可以通过两圆相减得到直线PQ的方程. 图式探路基于上述的图式分析,按照分析的思路进行探路.因为|OF|=c,所以以OF为直径的圆的方程为 即 x2-cx+y2=0. 将其与圆方程x2+y2=a2相减,得 从而 在圆x2+y2=a2中由垂径定理可知 即 4(a2c2-a4)=c4, 亦即 4(e2-1)=e4, 解得 e2=2, 即 故选A. 即 x2-cx+y2=0. 将其与圆方程x2+y2=a2相减,得 从而 在圆x2+y2=a2中,由垂径定理可知 即 |PQ|=|OF|. 评注上述图式检验可以一图不同形式表达进行检验,即换种思路进行解题,只要结果一致,即可说明结论正确. 当前数学教学存在重知识技能而轻数学思维、重思维结果而轻思维过程、思维指导不到位等问题[3].前文提到,一题多解是由于图形表达与代数转化过程不同,因此图式分析法有助于培养解题者的发散思维;当选定特定的模型时,解题过程往往局限在特定的数学模型下,因此图式分析法有助于培养解题者的定向思维.此外,类题通解是一种形(图形)似类比,有助于培养解题者的聚合性思维(定向思维).图式分析法在解题过程中宏观上的发散思维与微观上的定向思维相结合,最终在图式分析中呈现思维过程. 影响解题能力的因素主要包括数学问题本身、解题者自身以及教师的教学等因素.由于数学问题本身客观上存在一定的思维障碍,解题者对抽象的问题理解不清,教师对解题过程的引导方式不当,往往会导致解题难以进行.图式分析法主要是将抽象的问题图示化,在图形中将隐藏在条件与结论中的联系显现化,使问题直观化,同时帮助解题者从对图形的结构认识到对问题本身的理解,从而降低解题过程中思维上的障碍,更好地找到解决问题的方法,培养解题者的解题能力. 图示分析法在解题中的应用,不仅仅站在题目本身的视角,而是更直观地反映问题的本质,通过条件与结论内部的联系,以图形的视角审视问题,对问题进行充分的理解.在此基础上探索数学问题的解法与背景,从而在原有的数学问题上进行变式与编题[4],在解题方法上探索新的方法,从而训练解题者的数学思维,达到由一题到一类题的解题目的,因此图式分析法更加有助于培养解题者的创新能力.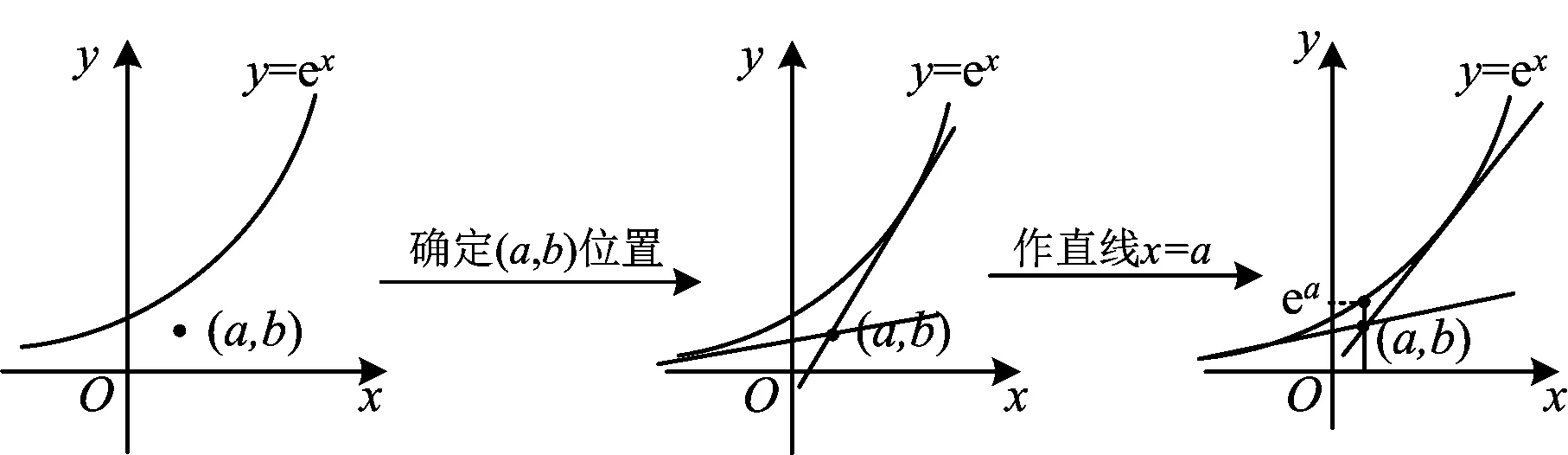
3 图式分析法的基本原则
3.1 图式等价性原则
3.2 图式模型化原则
3.3 图式甄选性原则

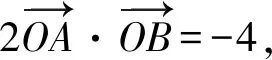

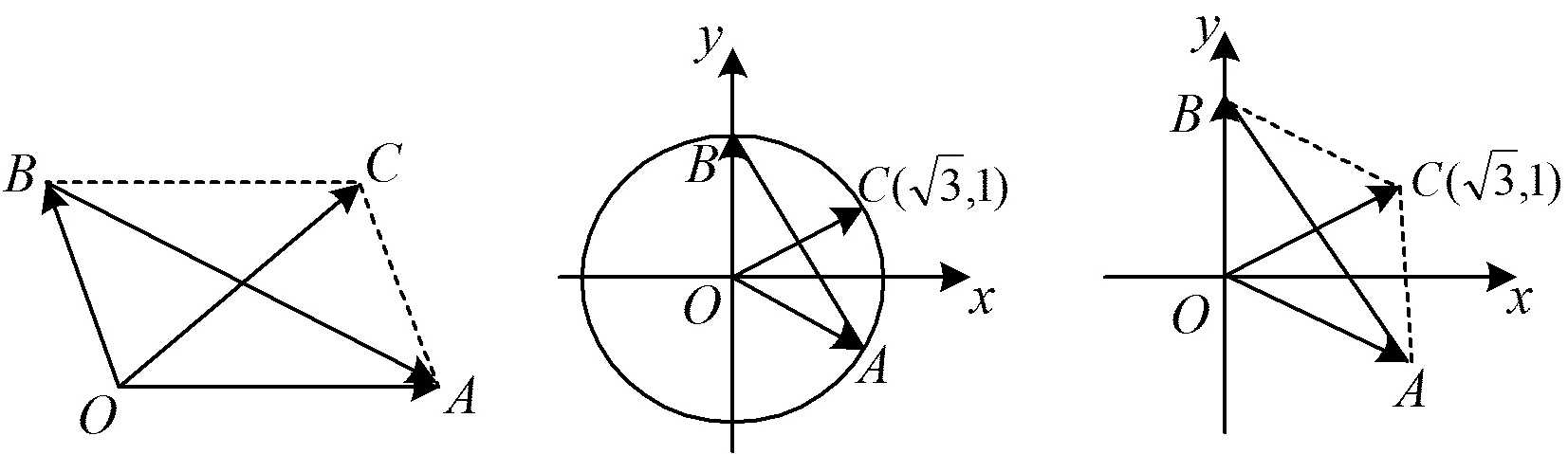
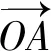
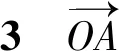
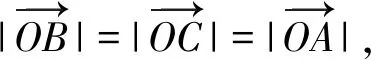

4 图式分析法的基本环节
4.1 图式审题
4.2 图式分析
4.3 图式探路
4.4 图式检验
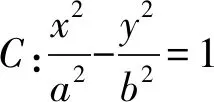
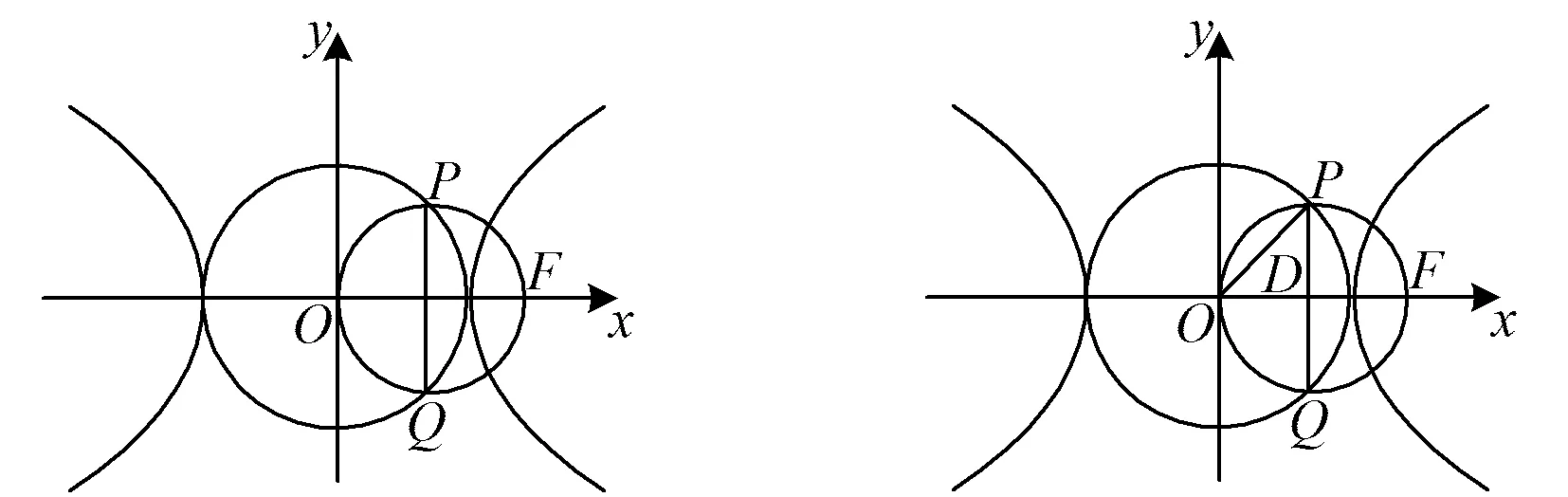

5 图式分析法的意义
5.1 培养解题者的发散思维与定向思维
5.2 提升解题者的解题能力
5.3 提高解题者的创新能力

